基于BP神经网络的机床热误差建模与分析*

辛宗霈，冯显英，杜付鑫，李 慧，李沛刚

(山东大学 a.机械工程学院; b.高效洁净机械制造教育部重点试验室,济南 250061)

0 引言

随着数控机床逐步发展，机床对加工精度的要求越来越高。机床误差包括热误差、几何误差及力引起的误差，其中热变形引起的误差占机床误差的40%～70%[1]。机床进给系统在运行期间摩擦产生热量，将导致滚珠丝杠的温度升高，而产生较大的热误差，直接影响机床精度。因此，对滚珠丝杠温度分布、热变形规律和热误差补偿技术进行数学建模研究，可以更好地分析热误差对机床加工精度的影响。

针对进给系统热误差，国内外学者在机床热误差建模和补偿方面进行了广泛的研究。主要方法有：神经网络模型法、多元线性回归法、有限元法和多体理论建立热误差模型方法等。夏军勇等[2]通过非线性时序模型预测丝杠在多变热源状况下的热弹性特征。OtakarHorejs等[3]在丝杠预紧效应基础上，提出热变形和轴承温升的变化关系。田国富等[4]提出了运用多元线性回归理论建模的方案，进行数控机床热误差的模型识别并达到了非常高的建模精度。陈诚等[5]提出了以ELMAN神经网络进行热误差建模，通过这种方法所建立的模型考虑了运行条件，准确性得到提高，且鲁棒性更强。张毅[6]在自然指数基础上提出通过多项式拟合描述机床定位误差和滚珠丝杠坐标位置关系的方法。

在上述论文所建热误差模型中，多数是用平台轴向热误差直接代替机床丝杠热变形，而实际上由于丝杠与平台之间传动链的影响,两者并不相等,因此需要建立数学模型表示两者间的关系。本文提出一种两步热误差预测方法，以BP神经网络对丝杠热变形量进行建模，然后通过多项式插值拟合来求得平台轴向热误差y与丝杠实际热变形量x之间的关系，构建出热误差预测模型。BP神经网络预测平台轴向热误差的方法作为直接法，与两步法进行对比。实验结果显示，两步法预测得到的热误差比直接法预测得到的热误差更接近于实测平台轴向热误差。

1 两步法原理

众所周知，进给驱动系统的定位误差很大部分由丝杠副的热变形引起，以丝杠轴向热变形量x表示[1]。

x=s(t)-s

(1)

其中，s是丝杠副某一点的位置。

机床开机自工作零点运动至指定行程处，为忽略定位误差，以此次激光干涉仪测量的工作台位移量作为初始值，热误差反映为在热力学实验过程中每次激光干涉仪测量值与其之间的差值。该误差由进给过程中所产生的热量引起，直接反映为工作台轴向位移量，因此称作平台轴向热误差y。

在大多数研究中，重点是系统温升如何影响运动的精确性和如何降低热效应，在多数热力学实验中，都是用平台轴向热误差直接代替机床丝杠热变形，而没有精确地以公式表示两者间的关系。实际上，激光干涉仪测得的误差不能简单的等同于丝杠热变形量，因为在滚珠丝杠与工作台之间存在着传动链。所以，平台轴向热误差是由丝杠热变形导致的，但二者并不相等。假设y和x之间的关系并非线性关系，因此可以通过多项式对两者之间的代数关系进行拟合：

y=λ0+λ1x+λ2x2+λ3x3+……+λnxn

(2)

式中，y是进给驱动系统在位置为s处的平台轴向热误差；λ0、λ1、λ2、λ3…λn是修正系数，反映了平台轴向热误差和丝杠热变形量的关系；x是丝杠在位置s处的热变形量；λ0、λ1、λ2、λ3…λn可通过多种方法求得，例如灰色理论系统、神经网络、最小二乘法、回归分析、多变量回归分析等，本文选择多项式拟合方法进行求解。

两步法基于BP神经网络和多项式拟合方法，第一步通过BP神经网络预测丝杠轴向热变形量x，第二步通过多项式插值拟合来求得平台轴向热误差y与丝杠轴向热变形量x之间的关系，通过这两个步骤得到实际平台轴向热误差。

2 热误差建模方法

图1所示为两步法流程图。本文以BP神经网络对丝杠热变形建模，建立动态丝杠热变形模型。实验基于滚珠丝杠平台进行建模，以热误差实验中的工作台速度v、运行时间t和工作行程l作为输入量，对以上各运行条件进行变化，测量丝杠热变形及温度，建立滚珠丝杠的热误差模型[5]。

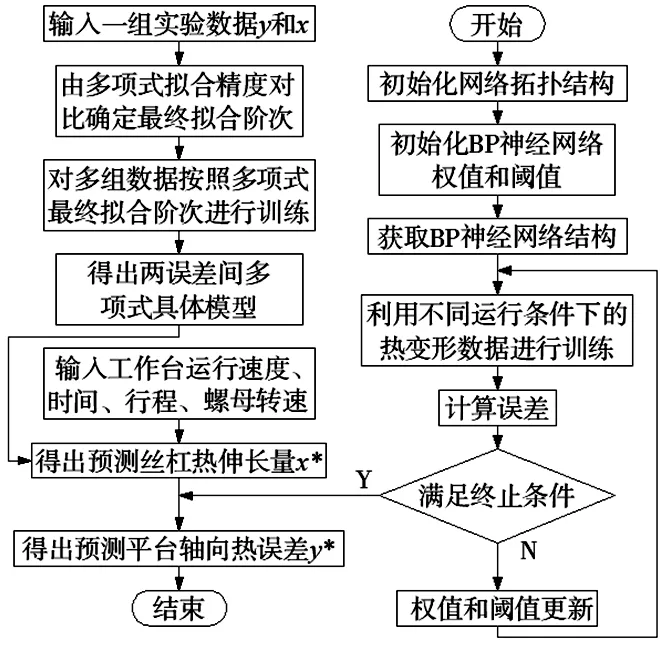
图1 两步法建模及预测流程图

在完成上述丝杠热变形建模之后，对于不同工况下的丝杠热变形和平台轴向热误差之间的关系进行多项式拟合求解。在得到误差数据后，采用最小二乘法对式(2)的参数求解。

3 机床温升、热变形量及平台轴向热误差测量试验

两步法首先需要通过BP神经网络对各运行条件和丝杠热变形进行建模处理，得出热变形量x与各变量之间的关系，然后通过对平台轴向热误差y与x进行多项式拟合，进而相结合得到进给系统的热误差模型。因此我们按照两步法所需要的各种数据进行实验设计并收集实验结果。

在实验过程中，工作载荷、工作台进给速度、行程以及工作时间对丝杠热变形都有影响，因此在实验设计时充分考虑以上工况的影响，在空载下制定实验方案如表1所示。

表1 实验方案

除测量阶段，从机床开机到达到热平衡，运动方式为定行程匀速往复运动，每隔10min停机测量一组数据。运动起点和测量起点均为工作零点。

系统温升、丝杠热变形量及平台轴向热误差测量原理图如图2所示，检测系统的硬件主要包括温度传感器(T1、T2、T3、T4)、温度变送器、微位移传感器(W1)、数据采集卡及激光干涉仪。其中近端轴承的温度由安装在固定端轴承处的T1检测，远端轴承的温度由T2检测，螺母组件的温度由安装在螺母处的T3检测，环境温度由T4检测。W1用于测量丝杠末端的热变形量[8]。激光干涉仪的反射镜安装在工作台上，干涉镜和激光头固定，用于测量平台轴向热误差。图3所示为滚珠丝杠运行平台测量实验图。

图2 系统温升、丝杠热变形量及平台轴向热误差测量原理图

图3 滚珠丝杠运行平台测量实验图

4 神经网络训练与多项式拟合

如图4所示为BP神经网络结构图[9]。

图4 BP神经网络结构图

BP神经网络训练过程中，将4个测温点测得的温升值组成阵列(4×19)作为输入变量，将这段时间采集的丝杠热变形量组成向量(1×19)作为输出变量[7]。以实验2和实验3对网络进行构建，并对其继续训练。对实验4的数据进行预测验证BP神经网络有效性，并得到丝杠各处的热变形。经过神经网络训练加入算法得到丝杠热变形整体分布，建立起丝杠热变形模型。

在完成丝杠热变形的模型建立后，将多组实验过程测得的y与x进行多项式拟合，拟合的过程中，一个非常关键的问题就是确定合适的多项式阶次。阶次如果太低，会导致拟合精确度低；阶次如果太高，计算难度增大，误差实施补偿困难，可能会出现过拟合的现象，使模型鲁棒性降低。在每次实验中，我们通过对不同阶次多项式在该实验条件下的热误差拟合精度对比，分析多组实验选择出适合的阶次作为最终拟合阶次。评价指标SSE为和方差，是拟合数据和原始数据对应点的误差的平方和；RMSE是均方根误差，是拟合数据与原始数据的平方和与观测次数m比值的平方根[6]。最终如表2所示选择n=3为最终拟合阶次。

表2 多项式拟合精度对比

在不同运行条件下，进行平台轴向热误差测量实验，在实验中同时测得平台轴向热误差及相应时间的丝杠热变形，根据式(3)得出平台轴向热误差与丝杠热变形间的数学模型。

y=λ0+λ1x+λ2x2+λ3x3

(3)

由实验测得的数据，对上式的参数进行求解，可以得到平台轴向热误差与丝杠热变形之间的具体模型[10]。

y=0.0076+0.9987x+6.2×e-5x2+8.4463×e-7x3

(4)

5 预测结果分析

由于单独分析两步法预测的热误差无法体现其优越性，因此在结果中将BP神经网络直接训练平台轴向热误差预测得到的热误差和两步法预测得到的热误差曲线图进行比较，方法一称作“直接法”。首先，通过实验1中的数据训练直接法和两步法。然后通过实验2～实验4验证模型的准确性，同时将模型逐步优化[5]。图5为实验1的温升数据及平台轴向热误差y。

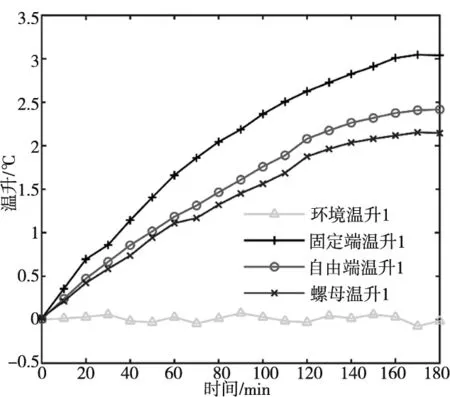
(a) 温升曲线

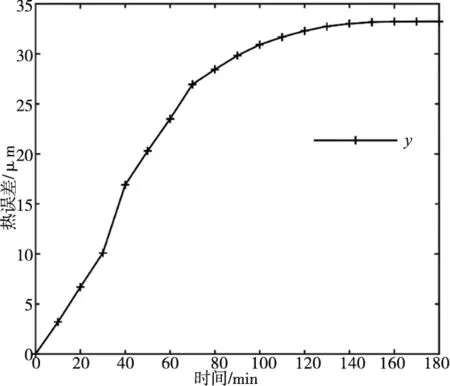
(b) 平台轴向热误差曲线 图5 实验1

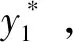
(a) 温升曲线

(b) 平台轴向热误差及预测模型统计 图6 实验2

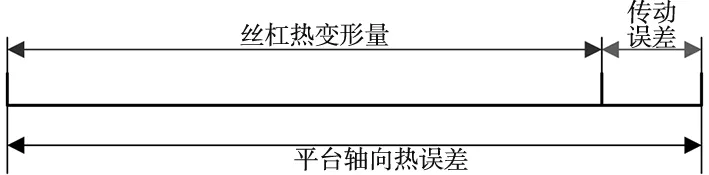
图7 平台轴向热误差组成

(a)温升曲线

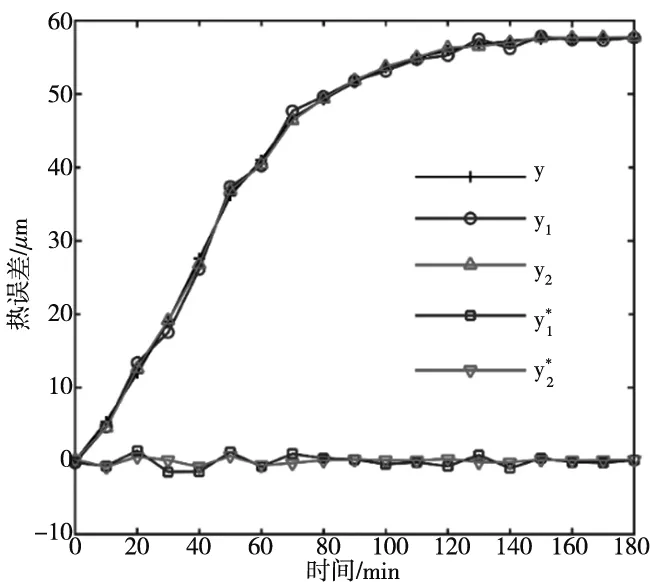
(b)热变形误差及预测模型统计 图8 实验3

(a)温升曲线

(b)平台轴向热误差及预测模型统计 图9 实验4

6 结论

本文提出了一种由BP神经网络预测丝杠热变形，然后通过多项式插值拟合来求得平台轴向热误差与丝杠实际热变形量之间的关系的复合建模方法，并通过实验验证了此方法的可行性。在实验过程中行程发生变化的情况下，BP神经网络预测热变形与多项式拟合热变形和平台轴向热误差两方法结合预测得到的热误差残差在-3.1～2.2μm内波动，此方法比单独以BP网络训练平台轴向热误差的方法具有更好的预测精度，更适合于工程应用。

DOI:org/10.1007/s00170-014-5606-0.