磁力耦合式高压流变仪测试系统测试参数修正

2019-09-05张永祥李秉繁

中国石油大学学报(自然科学版) 2019年4期

刘刚, 周莹, 苗青，张永祥, 李秉繁

(1.中国石油大学(华东)山东省油气储运安全省级重点实验室,山东青岛 266580; 2.中国石油油气储运重点实验室，河北廊坊 065000; 3.中国石油管道局工程有限公司,河北廊坊 065000)

随着对石油需求的不断增加,油气勘探开发逐步向深层次挖掘。对于高温高压深井、超深井,钻井液流变性受温度和压力的影响较大,所以实验室采用高压流变仪研究温度和压力对钻井液流变性带来的影响对高温高压井作业成败起着至关重要的作用[1-4]。而且近年来国内大力开展了气体驱油技术[5-8],矿场集输当中也常溶解一定的轻组分以降低原油的黏度来提高集输效率,降低能耗。管路内的原油通常为溶有一定气体的饱和溶气原油,然而目前中国常根据脱气原油凝点和黏度等流变参数来指导矿场集输系统的设计和运行,因此一些学者开始关注气体对原油的流变性的影响[9-13]。实验室中主要利用高压流变仪来研究气体驱油效果及驱替过程中原油流变性的影响规律。可见高压流变仪是研究高压溶气物料流变性[14-16]的重要手段,但由于磁力耦合作用,导致内磁环启动存在滞后问题[17-19],进一步加剧非稳态剪切测试结果的“失真”[20-25]。目前,尚未有学者对于磁力耦合式流变测试系统延迟启动问题进行研究。综上所述,磁力耦合式流变仪因磁力耦合存在延迟启动问题,从而造成高压流变仪启动瞬时测试数据出现较大偏差,导致研究测试物料的流变性时也存在较大偏差,这使得在进行矿场集输系统设计时产生更大的误差,会影响实际站场运行,存在安全隐患及增加能耗。对于非稳态剪切流动过程中流变测试结果“失真”问题,流变仪厂家并未给出修正,其他学者也未深入研究。恒剪切率加载是最为常用的流变条件。为此,笔者根据恒剪切率加载条件下流变仪传动过程的扭矩平衡建立磁力耦合式旋转流变仪启动过程的物理传动模型,并以HAAKE-MARS60高压流变仪为例,对牛顿流体恒剪切率加载条件下测量参数进行分析,并利用所建立的模型进行修正。

1 磁力耦合式旋转流变仪测试系统磁力耦合传动过程物理模型建立

图1为磁力耦合式旋转流变仪测试系统。其中包括外磁环、内磁环、压力单元腔体以及转子、宝石轴承等[26-28]。流变仪启动过程中的扭矩并非都用于剪切流体,部分扭矩用于加速内外磁环、马达和转子旋转以及摩擦损失。

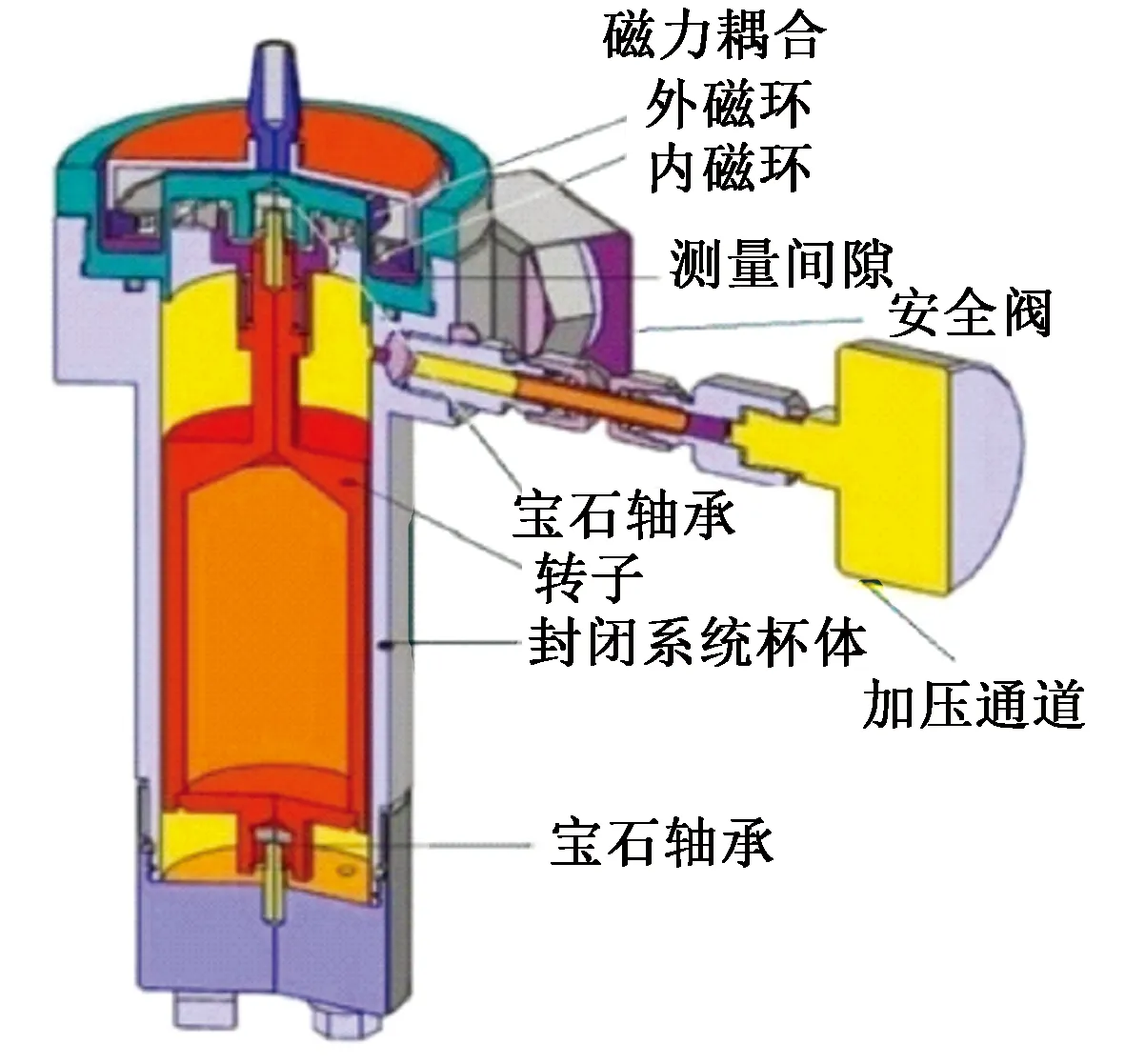
图1 磁力耦合式流变仪测试系统Fig.1 Magnetic coupling rheometer test system

1.1 物理模型建立

图2为磁力耦合式旋转流变仪测试系统的磁力耦合传动过程。在流变仪启动瞬间,马达扭矩达到设定值,但在向下传递的过程中,由于流变仪外磁环作非匀速转动,将损失一部分扭矩,并且在传动过程中会损失部分传动力矩ΔM,传递给内磁环的力矩M0,但由于ΔM很小可忽略不计[29-30],内磁环的扭矩一部分用于内磁环的加速和摩擦造成的损失,剩下的才是真正作用于负载的扭矩,在此假设下建立模型如下。

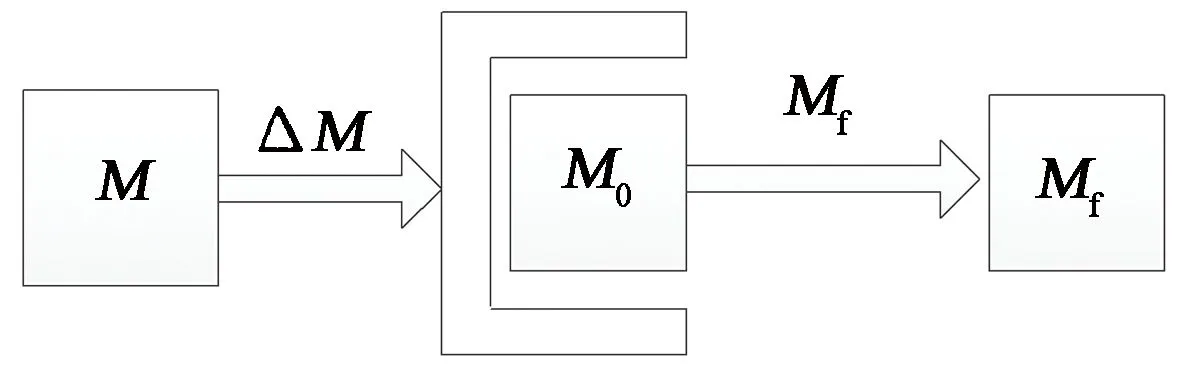
图2 磁力耦合式旋转流变仪测试系统的磁力耦合传动过程Fig.2 Magnetic coupling driving process of magnetic coupling rotary rheometer testing system

考虑马达和外磁环惯量,建立外磁环扭矩平衡关系式为

(1)

式中,M为流变仪马达启动扭矩,N·m;M0为磁力耦合扭矩,N·m;θ1为外磁环角位移,rad;J1为外磁环转动惯量,kg·m2;Jmonitor为马达及夹具惯量,kg·m2。

考虑内磁环及测量转子惯量和宝石轴承摩擦损耗,建立内磁环扭矩平衡关系式为

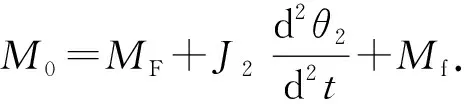
(2)

式中,MF为负载扭矩,N·m;Mf为宝石轴承摩擦扭矩,N·m;θ2为内磁环角位移,rad;J2为内磁环及测量转子转动惯量,kg·m2。

根据流变仪自身机械特性,内外磁环磁力耦合关系式为

M0=Mmaxsin[m(θ1-θ2)] .

(3)

式中,Mmax为最大静磁力矩,N·m;m为磁极个数。

初始条件为

1.2 物理模型中各参量特性

1.2.1 负载扭矩

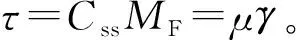
1.2.2 宝石轴承摩擦扭矩

控制流变仪空转，采用剪切速率阶跃增加的方法,待转速恒定后,测试不同转速条件下宝石轴承的摩擦扭矩Mf,如图3所示。宝石轴承摩擦扭矩随着内磁环转速N2的增加而增大,且呈现较好的线性关系。拟合可得

Mf=aN2+b=0.061 49+0.001 791N2.

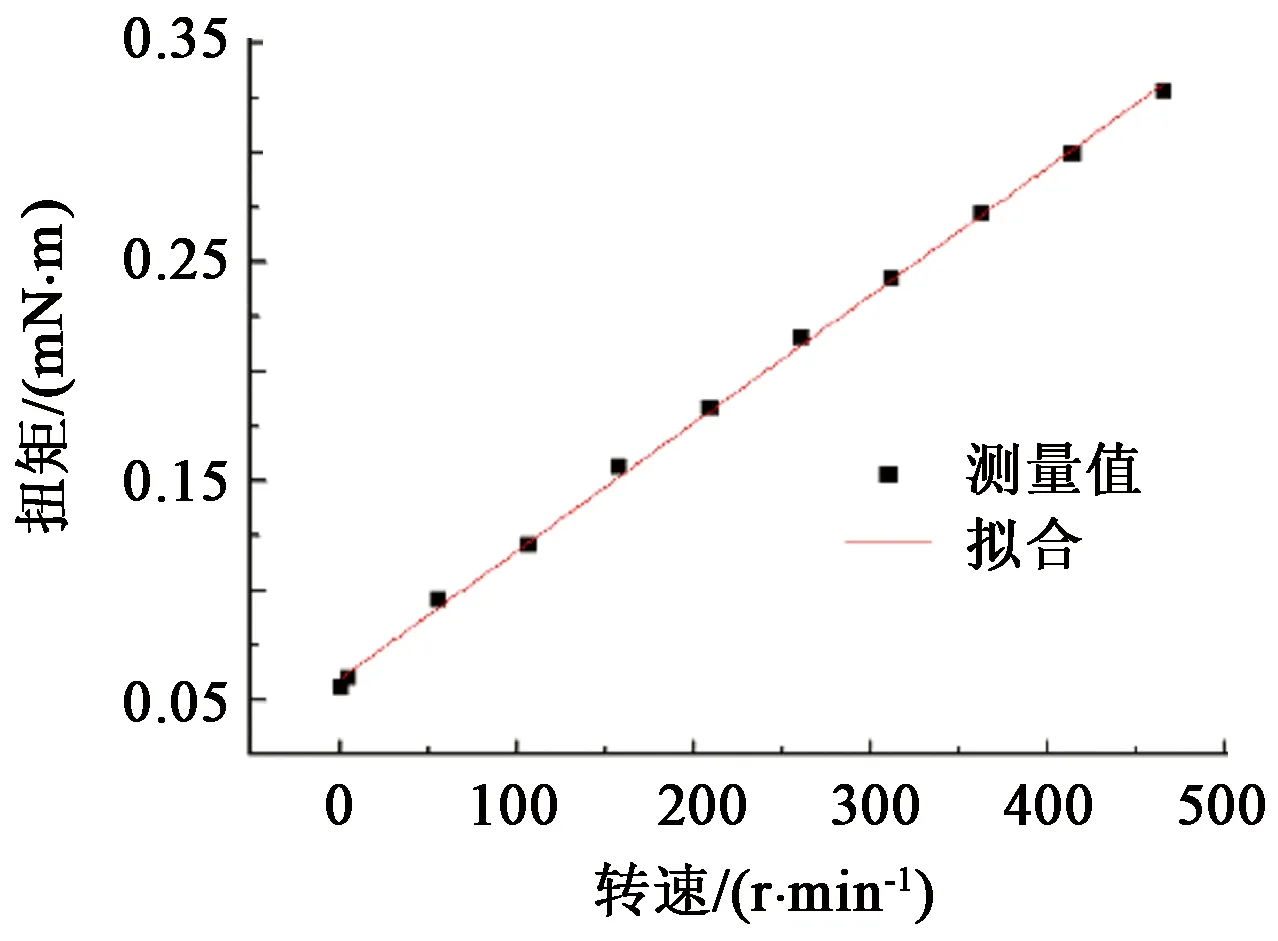
图3 摩擦扭矩随转速变化关系Fig.3 Variation of friction torque with rotational speed

1.2.3 马达及夹具惯量计算

(4)

式中,Itotal为总的转动惯量,kg·m2;CSS为应力-扭矩转换系数,数值为5 511 Pa/(N·m);N1为外磁环转速,r/min。

为了探究马达和夹具的总转动惯量,采用空载测试的方法获得不同恒定应力下的转速-时间曲线,如图4所示。通过计算不同应力条件下系统转动惯量的真实值进而确定马达和夹具的总转动惯量,可得Itotal=456.081 1×10-6kg·m2,扣除相应的内、外磁环及测量转子质量惯量,可得马达及夹具惯量约为234.581 1×10-6kg·m2。

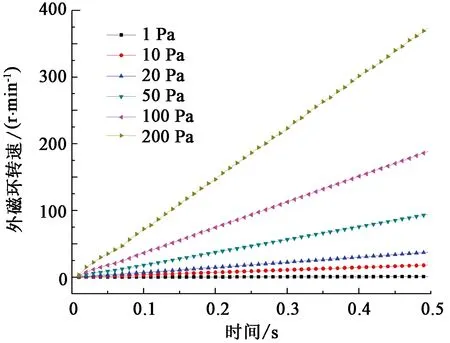
图4 不同恒应力启动条件下空载转速随时间变化关系Fig.4 Variation of rotational speed with time under different constant stress during initial testing stage with no load

1.3 模型求解

将式(3)分别代入式(1)及式(2)中,整理可得

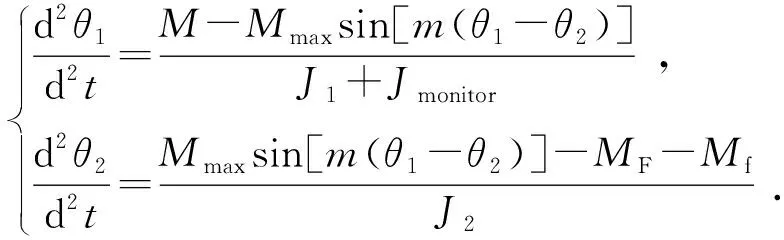
(5)

由式(5)可看出:流变仪磁力耦合传动过程物理模型为二阶非线性偏微分方程组。由流变仪测得外磁环扭矩测试值Mtest和外磁环转速测试值N1,采用追赶法编程求解式(5),可得内磁环的相关物理参数,进而计算得到测试流体的流变参数。

通过对外磁环转速积分可得外磁环角度为

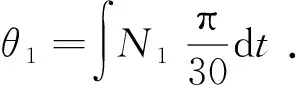
(6)

根据外磁环的扭矩平衡公式(1)和磁力耦合特性公式(3)可以算出内磁环转动角度为

综上可见，小型水库安全管理应落实专业人员管理，发现问题及时处理，要加强小型水库的抗洪能力及应急保障能力，重视巡视检查与应急能力建设，保障工程安全。

(7)

式中,w1为外磁环角速度,rad/s。

对内磁环转动角度求导可得到内磁环转速N2为

(8)

根据内外磁环扭矩平衡公式(1)和(2)可得到负载扭矩MF为

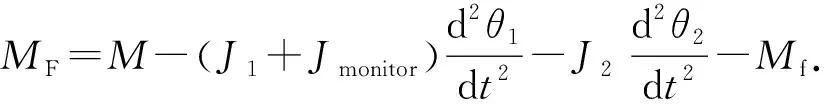
(9)

根据运动参数进行流变参数的换算,可得到剪切应力τ为

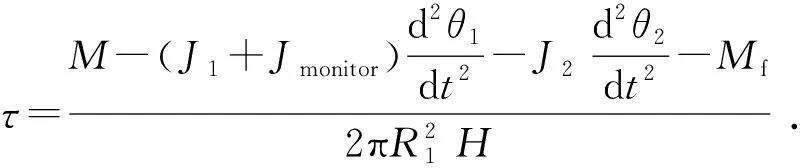
(10)

式中,R1为转子半径,mm;H为转子高度,mm。

(11)

式中,CSR为剪切速率-转速转换系数,数值为2.147 8 s-1/min-1。

2 结果及其讨论

实验所用的4种牛顿流体为国家计量科学院提供的标准黏度液,标物编号分别为GBW13608、GBW13609、GBW13610和GBW13611,其基本物性参数如表1(d为内、外转筒间隙)所示。标准黏度液是在常压条件下,20℃时标定的标准流体,可用于流变仪测试系统的测量标定。

表1 常压条件下20 ℃时标准黏度液基本物性参数

2.1 磁力耦合式流变测试系统内磁环真实流变信息求解

2.1.1 内磁环转速

根据恒剪切速率加载条件下测得不同标准黏度液外磁环加载扭矩M和外磁环转速N1,利用磁力耦合传动物理模型计算得到内磁环转速N2。

图5为不同标准黏度液在20 s-1(对应转速为9.3 r/min。)恒剪切速率加载条件下启动时内磁环转速、外磁环转速随时间变化曲线。由图5可以看出,启动初始时刻内磁环启动滞后于外磁环;且随着时间增加,内磁环转速震荡上升,最终内外磁环达到同一转速。

同样比较40 s-1剪切速率加载条件下启动时内磁环转速、外磁环转速随时间的变化关系,结果如图6所示。比较图5和图6可以看出,20 s-1加载条件下内磁环的转速震荡比40 s-1的明显。

表2为不同标准液在不同剪速加载条件下启动时内磁环转速波动幅度。由表2可以看出,黏度相同情况下,1 s-1恒剪速加载条件下内磁环转速的波动幅度最大。随着剪切速率增大,内磁环转速波动幅度逐渐减小。剪切速率加载条件相同情况下,黏度为4 963.3 mPa·s的黏度液内磁环转速波动幅度最大,随着黏度降低,内磁环转速波动逐渐减小。

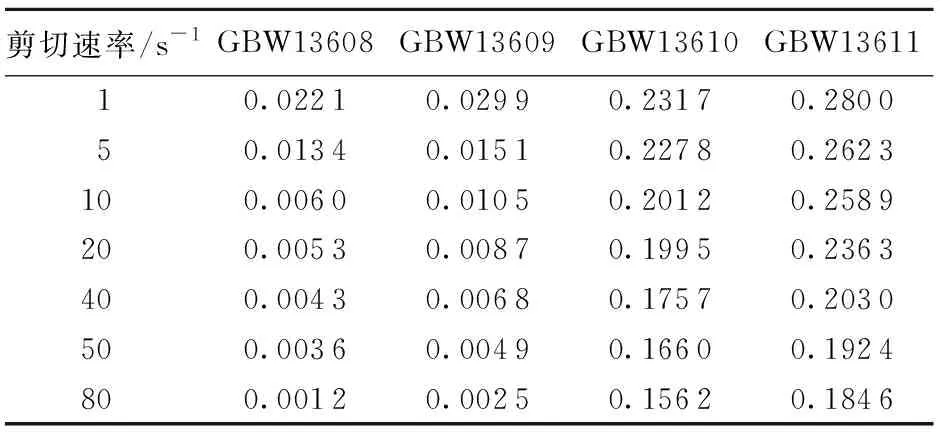
表2 不同标准液恒剪速启动时内磁环转速波动幅度Table 2 Fluctuation of internal rotor speed at constant shear rate startup of different standard fluids r/min

由此可以得出:标准液黏度越大,剪切速率越小,内磁环转速波动幅度越大。这是由于内、外磁环的转动受磁力偶合扭矩以及负载扭矩的影响,而流变仪磁力耦合扭矩是以内、外磁环转角差为自变量的正弦周期函数。因此在流变仪初始启动阶段,内磁环转速震荡上升,当流变仪稳态剪切时,其内、外磁环转角差为恒定常数,内、外磁环达到同一转速。由于加载边界反馈控制时调节频繁,剪速会呈现明显波动,且在试样黏度较大时更为明显。

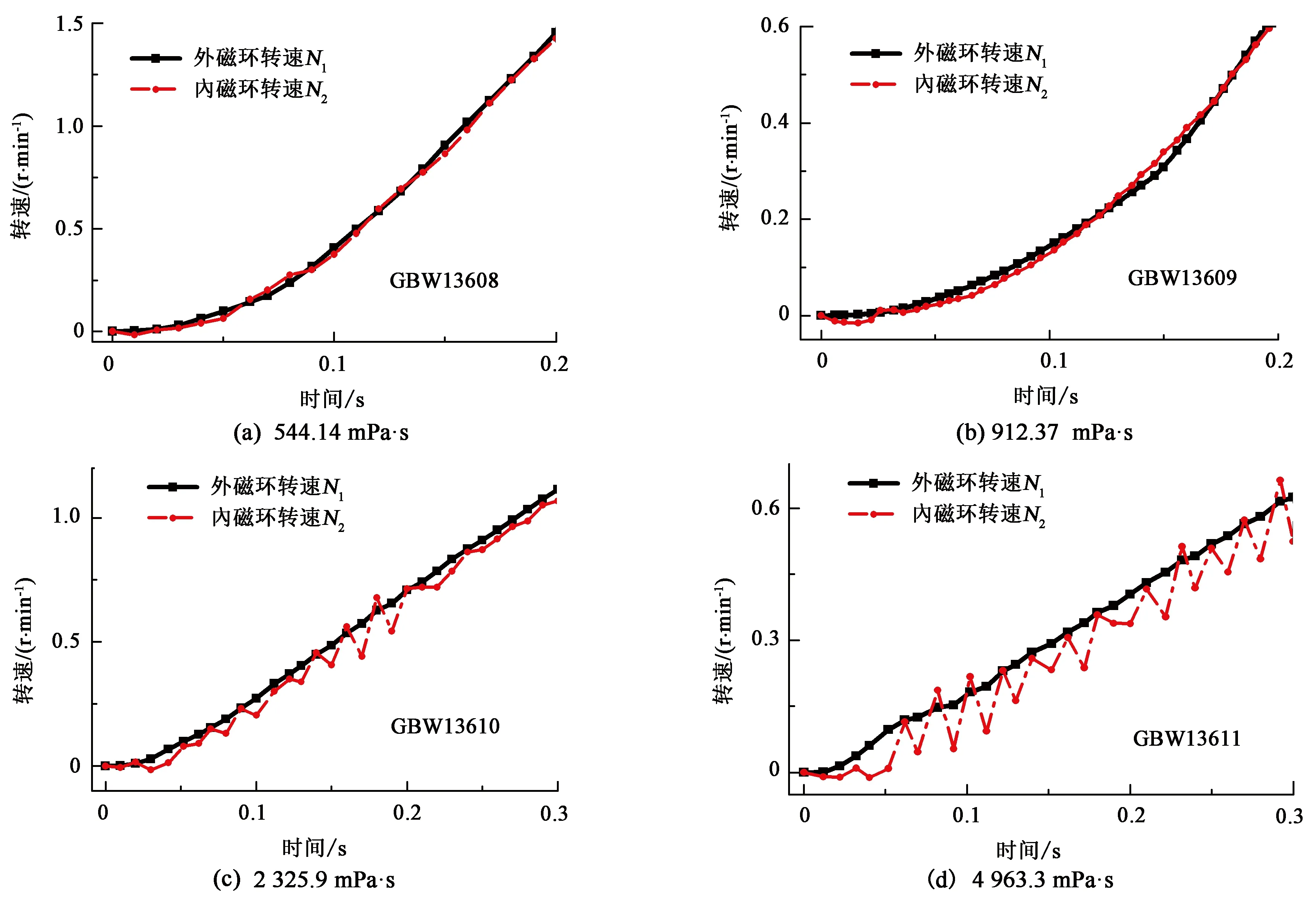
图5 不同标准液恒剪速启动时内、外磁环转速随时间变化曲线(20 s-1)Fig.5 Variation of internal and external rotation speeds with time at constant shear speed of different standard liquids (20 s-1)

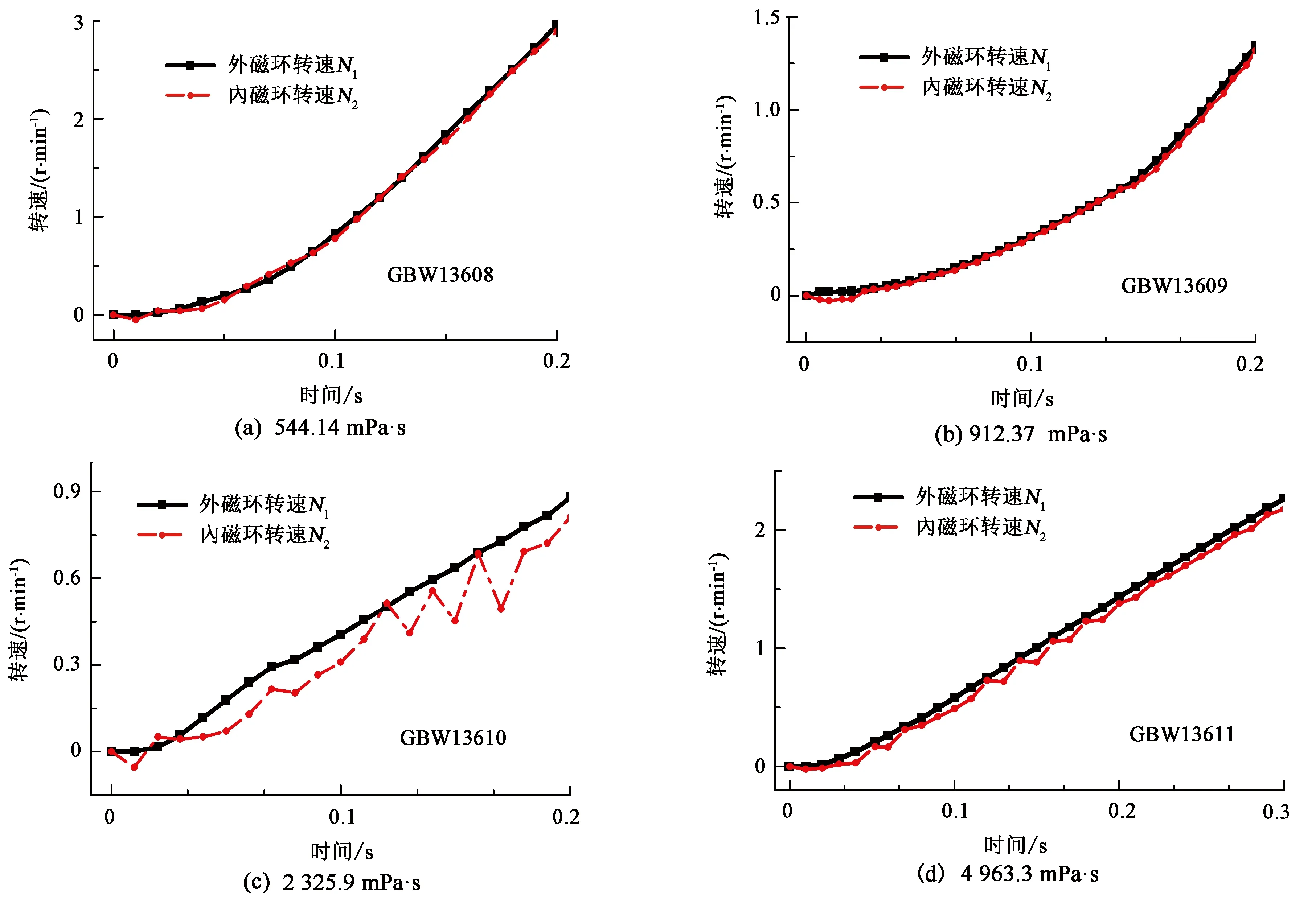
图6 不同标准液恒剪速启动时内、外磁环转速随时间变化曲线(40 s-1)Fig.6 Variation of internal and external rotation speeds with time at constant shear speed of different standard liquids (40 s-1)

2.1.2 内磁环剪切应力

根据恒剪切速率加载条件下测得不同标准液外磁环加载扭矩和外磁环转速,利用公式(10)求解得到内磁环的剪切应力。并与外磁环测得的剪切应力进行比较,得到内、外磁环的剪切应力随时间变化曲线(图7、8)。20 s-1恒剪速加载条件下的结果如图7所示。流变仪初始启动阶段,内磁环转子表面的剪切应力存在从零增加至预设值的过程,并且内磁环转子表面的剪切应力要低于外磁环的剪切应力。

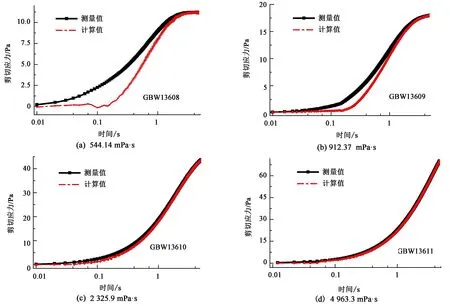
图7 不同标准液恒剪速启动时内、外磁环剪切应力随时间变化曲线(20 s-1)Fig.7 Variation of internal and external magnetic ring stress with time when starting with constant shear speed of different standard liquids (20 s-1)

同样对40 s-1恒剪切速率加载条件下的内外磁环剪切应力进行比较,可以看出同20 s-1恒剪切速率加载条件下的内磁环剪切应力变化规律一致。比较图7、8可以看出,内磁环剪切应力明显低于于外磁环测得的剪切应力,并且黏度越小,剪切速率越大,内、外磁环表面的剪切应力差异越明显。这是由于剪切速率越大,黏度越小,则用于加速旋转系统的扭矩损失和摩擦损失越大,真正用于剪切流体的剪切力越小,因此内、外磁环对应的剪切应力差异越大。

2.1.3 牛顿流体黏度修正

根据恒剪切速率加载条件下测得不同标准黏度液外磁环加载扭矩M和外磁环转速N1,利用公式(11)求解得到标准液的真实黏度。并与实测黏度进行比较,得到不同标准液恒剪速条件下黏度测量值和修正值。

图9为20 s-1恒剪速加载条件下黏度测量值和修正值。由图9可看出实测黏度曲线随时间先增大后减小直到达到稳态,这是由于实测黏度的计算并未区分瞬态测试过程中总扭矩和真正用于剪切流体的扭矩,以及瞬态测试过程中外磁环转速和内磁环转速。因此,流变仪数据处理系统瞬态过程的黏度是存在偏差的。而利用流变仪磁力耦合传动过程物理模型求解得到的黏度相比实测黏度明显越接近牛顿流体的真实黏度。但求解得到的黏度仍然存在一定的波动情况,主要原因有:①求解过程中需用到内外磁环角位移的二阶导数,而流变仪测试数据取点不够密,导致黏度修正值存在一定的波动;②在较低剪切速率加载条件下,宝石轴承的摩擦扭矩Mf可能并非严格与转速成线性关系;③加载边界的反馈控制调节频繁,所采集的应力或剪速会呈现轻微波动,黏度作为应力与剪速的计算值也不可避免地出现数据波动;④模型假设测量转子表面的转动参数等于测量物料的转动参数,忽略了测试物料的惯性。

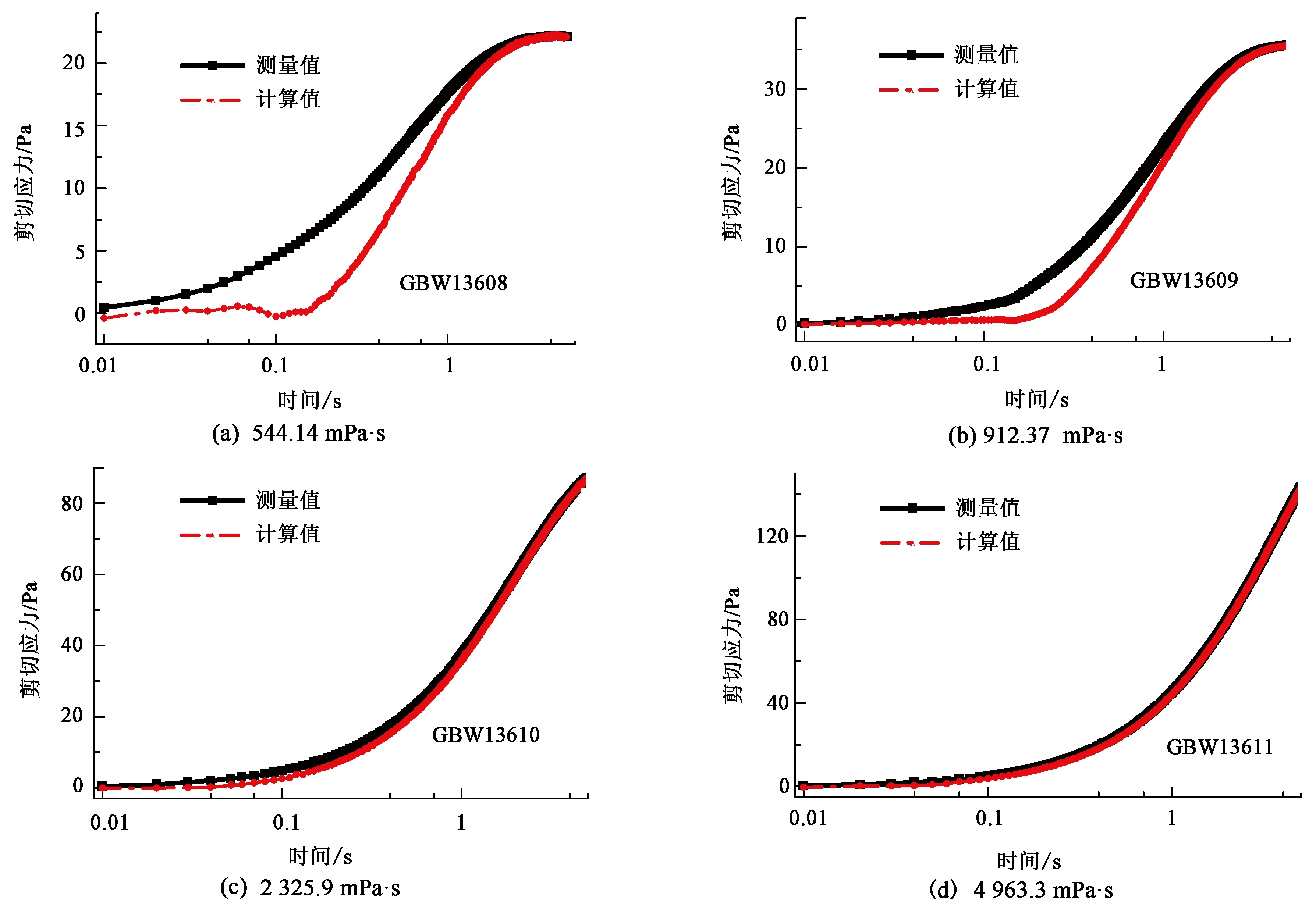
图8 不同标准液恒剪速启动时内、外磁环剪切应力随时间变化曲线(40 s-1)Fig.8 Variation of internal and external magnetic ring stress with time when starting with constant shear speed of different standard liquids (40 s-1)

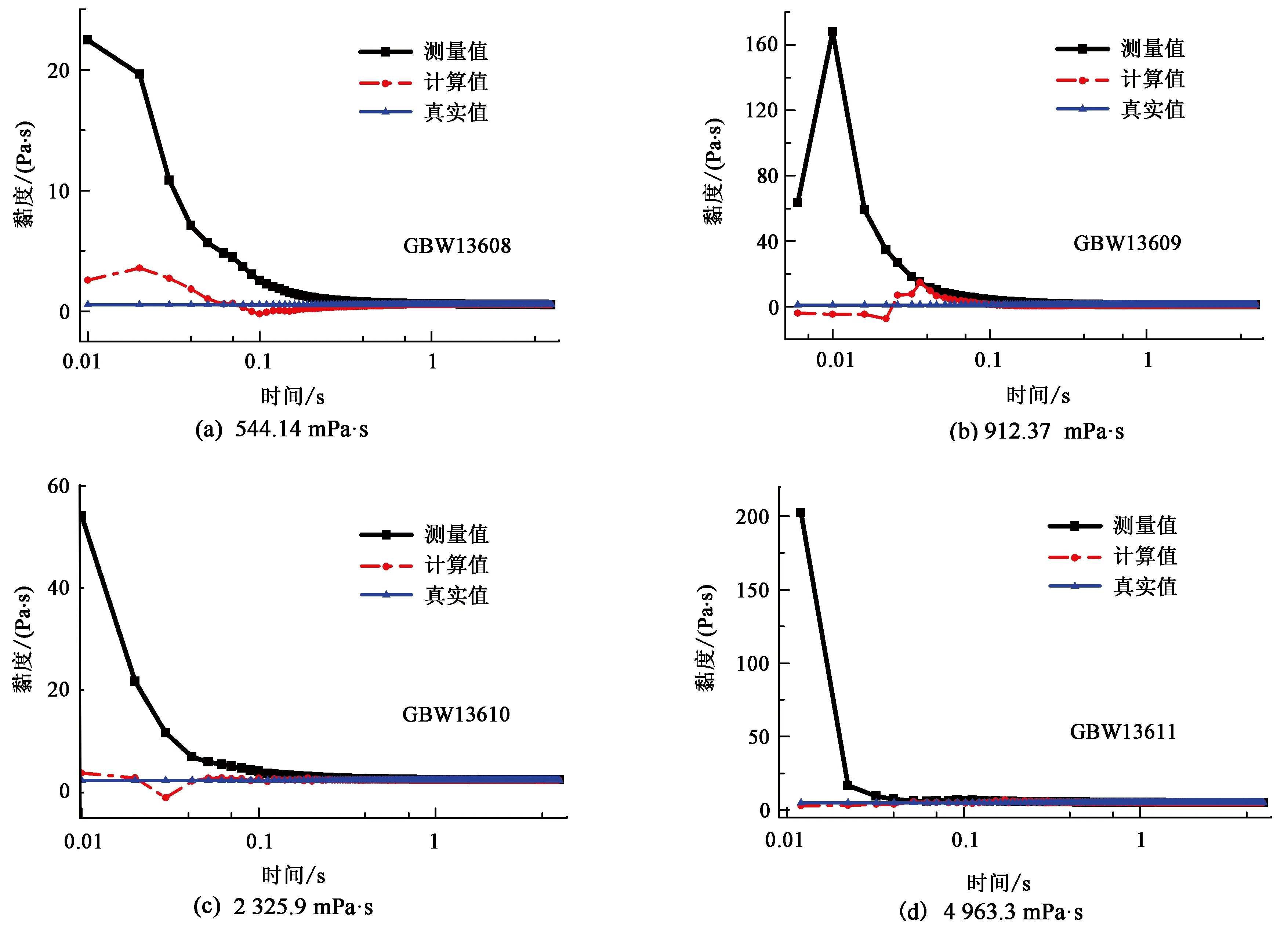
图9 不同标准液恒剪速条件下黏度实测曲线和修正曲线(20 s-1)Fig.9 Variation between viscosity test and correction under constant shear rate of different standard liquid (20 s-1)

图10为40 s-1恒剪切速率加载条件下的表观黏度测量值和修正值。比较图9和图10,可以看出黏度越大,剪切速率越大,计算得到的黏度越接近真实值。由于黏度和剪切速率越大,外磁环剪切速率线性增加,不会出现大幅度波动。因此内外磁环角位移的二阶导数比较连续,黏度修正值越接近真实值。