管内可控万向铰接柔性杆接触非线性有限元分析
2019-09-05徐亭亭李巧珍张佳贺
罗 敏, 徐亭亭, 王 晶, 李巧珍, 张佳贺
(1.东北石油大学机械科学与工程学院,黑龙江大庆 163318; 2.东北石油大学数学与统计学院,黑龙江大庆 163318)
管内可控万向铰接柔性细长杆是超短半径侧钻水平井的特有结构,柔性杆多段铰接使其能顺利通过曲率半径较小的弯曲井眼。在钻进过程中,各段柔性杆不在一条直线上,同时还会与外管产生随机多向接触,使摩擦力增大,引起载荷传递损失,所以管内可控万向铰接柔性细长杆的力学分析对超短半径水平井钻井具有重要意义。针对柔性钻具,国内学者开展了相关的力学分析。苏义脑等[1-2]将铰链接头视为平面铰链,建立了铰接式柔性钻具的力学模型,推导出任一铰链处的受力状况,确定了钻压与大钩载荷之间的关系。帅健等[3-4]采用凝聚自由度方法,建立了铰接式钻具组合的二维有限元模型,并对其进行了单因素影响分析。高加强[5]和LIU等[6]考虑柔性钻杆的结构特点和受力状态,建立了单节柔性钻杆的三维有限元模型,实现了对柔性钻杆的强度评价。在国外,超短半径水平井钻井多采用高压射流技术[7-11]。Gary[12]设计了柔性钻井工具,但由于其柔度和强度有限,并没有应用到超短半径水平井钻井中,需要进一步研究和改进。综上所述,国内外学者对于铰接连接的柔性细长杆与外管的接触问题研究较少,目前的研究方法均局限于二维情况,且铰接处没有考虑相对转角限制,因此笔者对可控万向铰接柔性杆与外管接触非线性问题开展研究。
1 柔性杆与外管接触模型的建立
假设外管的轴线为任意圆弧与直线的组合,外管内铰接柔性杆的结构示意图如图1所示。将柔性杆和外管看作是三维有限应变梁单元,单节柔性杆之间通过万向铰连接,柔性杆在外管内的径向运动受外管内壁约束,致使杆管之间发生接触,单独的空间梁单元模型不能解决铰接柔性杆与外管边界的接触非线性问题。本文中采用空间梁单元、万向铰单元和接触单元的混合有限元模型解决可控万向铰接柔性杆与外管接触问题。

图1 外管内铰接柔性杆结构示意图Fig.1 Schematic diagram of hinged flexible rod in outer tube
1.1 可控万向铰接梁单元的分析模型
采用有限元法,用两节点十二个自由度的空间梁单元对柔性杆进行离散,整体平衡方程可表示为
F=Kδ.
(1)
式中,F为节点力列阵;K为总体刚度矩阵;δ为节点位移列阵。
基于可控万向铰可在两个方向上发生相对转动的特点,通过两个节点对其进行定义,节点I和J重合,每个节点具有3个平动位移以及3个转动位移,万向铰单元坐标表示如图2所示,两个节点须定义局部直角坐标系描述运动约束,y轴方向为传动轴方向。可控万向铰是在万向铰的基础上,在两个方向上只能相对转动固定的角度,当达到转动限制度数时,连接方式就变为刚性连接,其运动由机构问题转化为结构问题。

图2 万向铰单元坐标示意图Fig.2 Coordinate representation diagram of universal joint element
任意给定时刻万向铰单元的运动约束表示为位移约束和转动约束。
位移约束为
uI=uJ.
(2)
转动约束为
(3)
式中,uI和uJ分别为节点I和节点J的线位移向量;eIx、eJz、eIy和eJy均为沿各局部坐标系相应方向的单位向量。
节点I和节点J的局部坐标系相对位置的第一和第三卡登角[13],分别为

(4)

(5)
两局部坐标系相对转角的改变Δφ和Δψ可表示为
Δφ=φ-φ0,
(6)
Δψ=ψ-ψ0.
(7)
式中,φ0和ψ0分别为节点I和节点J的局部坐标系相对位置的初始第一和第三卡登角。
当Δφ和Δψ达到转动限制度数时,万向铰单元的运动约束表示为
uI=uJ,θI=θJ.
(8)
式中,θI和θJ分别为节点I和节点J的角位移向量。
由上述分析可知,万向铰单元由于节点位置重合,因此其没有形函数,只通过给定运动约束实现其功能,将万向铰单元与梁单元的平衡方程相结合,经过坐标转换和拼装过程得到万向铰连接的梁单元的总体平衡方程为
F=Knδ.
(9)
式中,Kn为整体坐标系下万向铰连接的梁单元的总体刚度矩阵。
1.2 柔性杆与外管接触分析模型
1.2.1 接触单元描述
为分析柔性杆与外管的接触问题,创建接触单元和目标单元,分别依附在柔性杆的外表面和外管的内表面,接触单元和目标单元与所依附的梁单元满足变形协调条件。当柔性杆与外管未发生接触时,它不影响柔性杆的运动,当接触时,其刚度为某一给定值,阻抗接触体之间的相互侵入。
1.2.2 摩擦模型
当柔性杆与外管接触时,接触面有法向接触压力,若柔性杆与外管发生相对滑动,有轴向摩擦阻力存在,本文中采用经典的库伦摩擦模型,即
Ff=μP.
(10)
式中,P为法向接触压力,N;μ为摩擦系数;Ff为轴向摩擦力,N。
1.2.3 接触判定条件
理论上,两物体在变形过程中会出现分离状态和侵入状态,而实际上侵入状态不可能发生。为了消除这种可能性,引入间隙函数h定义两物体的接触状态,当间隙函数小于零,可判定接触存在。
定义两根梁的间隙函数的基础是找到一对最接近的点Pm和Pn,如图3所示。曲线上任意点的位置可以分别由局部坐标系em和en定义。

图3 梁在梁内接触模型Fig.3 Beam in beam contact model
在全局坐标系(X,Y,Z)中,曲线上的每个点都与位置向量xm或xn相关联。由于间隙函数必须始终在当前构型中确定,在增量处理变形过程的每次迭代中,这些向量都对应于当前梁的构型。它们可以表示为初始构型点的位置向量Xm、Xn和位移向量um、un的和,即
(11)
两根梁最接近点Pm和Pn在曲线上的位置向量xm和xn必须满足连接线与这些点上与曲线相切的直线之间的正交条件。这些条件可以表示为

(12)
其中
在一般情况下,当梁的初始轴线发生变形时,式(12)构成一组非线性方程组。方程组的解可以通过局部坐标系em和en的形式给出,它描述了最近点Pm和Pn的位置。对式(12)进行线性化处理,计算局部坐标增量Δem和Δen为
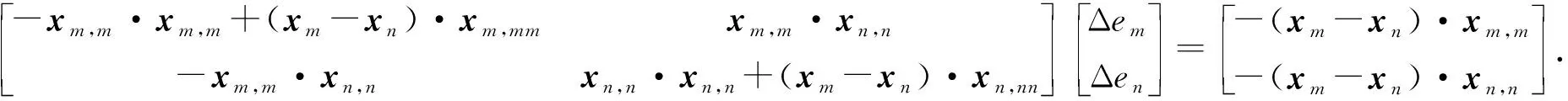
(13)
其中
求出两根梁最接近点Pm和Pn的位置后,可以计算出它们之间的距离Δ为
Δ=|xm-xn|.
(14)
在计算出最接近点的距离基础上,间隙函数h可由几何关系确定为
h=rw-rc-Δ.
(15)
式中,rw为外梁的内径,m;rc为内梁的外径,m。
基于接触表面沿法线方向的接触间隙,并满足接触边界上的变形协调,采用增广拉格朗日算法计算法向接触力Ft。
综合可控铰接连接的机构问题及接触非线性问题,结合梁单元、万向铰接单元和接触单元,可得到实现分析外管内可控万向铰接柔性杆接触非线性的整体平衡方程为
F+Ft=(Kn+Kt)δ.
(16)
式中,Ft为接触力列阵,是节点位移的函数;Kt为接触刚度矩阵。
由于式(16)第一次求得的解通常不能满足接触判定条件,须反复迭代计算,直到得出全部满足接触判别条件的解为止,因此选用修正的牛顿辛普森法进行求解。
2 模型验证
内杆弹性模量E为210 GPa,直径为20 mm,长为2l=2 m,内杆与外管间隙δ=3 mm。 内杆两端固定,中间铰接处受集中载荷作用F=80 N,外管全固定,如图4所示。QA、QB、MA和MB分别为A点和B点的支反力及弯矩,FC为接触反力。
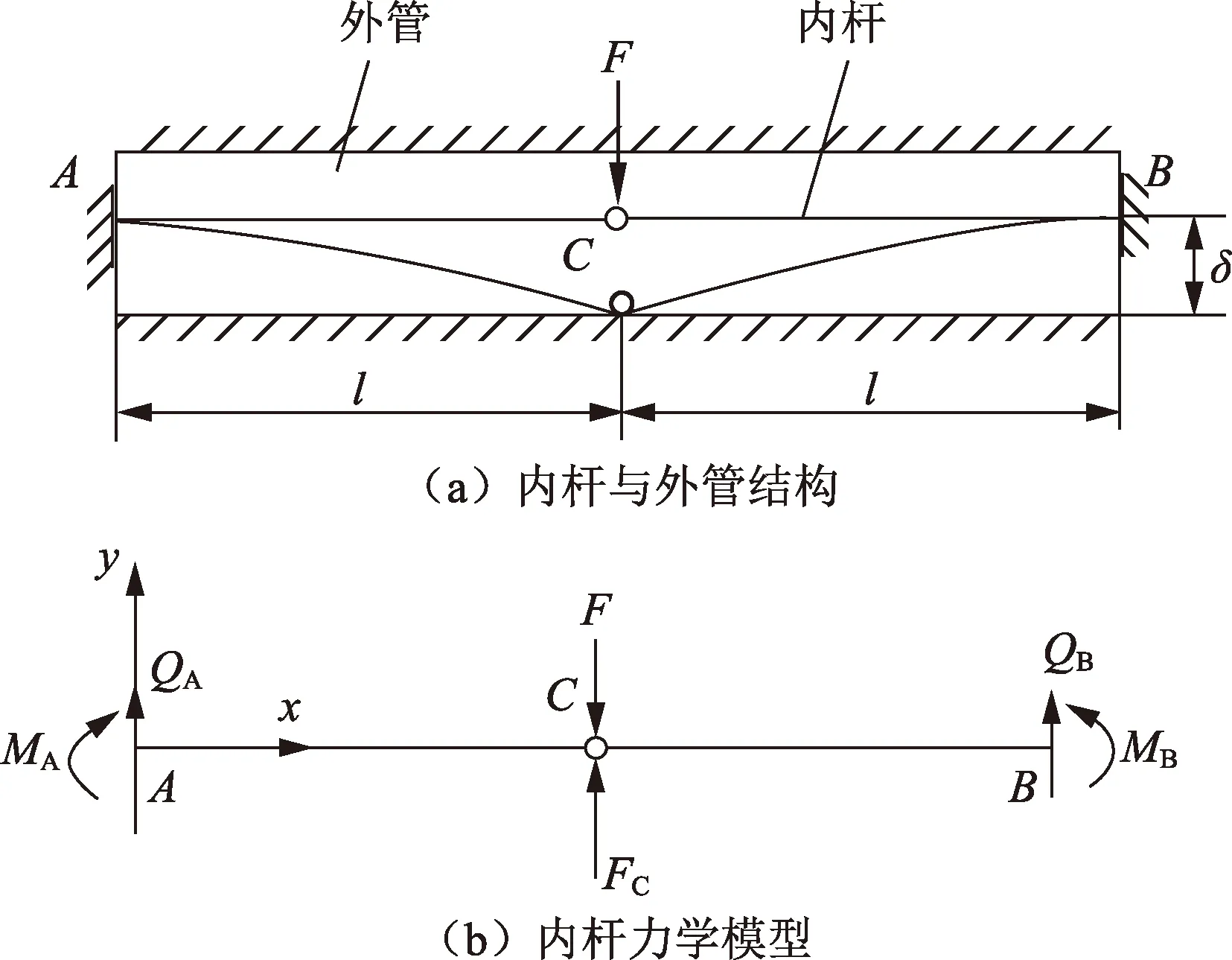
图4 内杆与外管结构及力学模型Fig.4 Structure and mechanical model of inner rod and outer pipe
根据结构的对称性和平衡条件可知,内杆与外管接触点位于C点,内杆AC段在F和FC单独作用下的挠度分别用yF和yFC表示,其挠曲线微分方程为
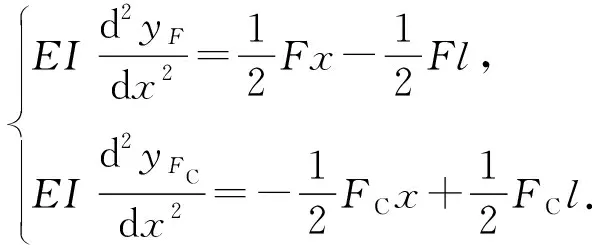
(17)
在固定端A,转角和挠度均等于零,即

(18)
内杆AC段的总挠度为ysum,其值等于yF与yFC的和,内杆与外管在x=l处发生接触,则
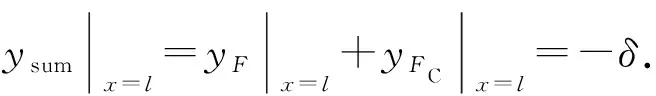
(19)
根据式(17)和(18)可确定yF和yFC的表达式,最后根据式(19)确定FC,FC可表示为
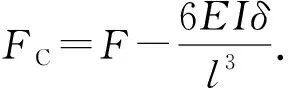
(20)
采用本文中的铰接柔性杆与外管接触模型(不限制铰接处转动度数)和数值求解算法,所得结果与解析解进行对比,结果见表1。

表1 计算结果对比
由表1可知,C点弯矩为0,验证了铰传递力不传递弯矩的特点,理论解与数值解最大误差仅为1.08%,接触力的误差仅为0.64%,验证了接触模型的正确性。
3 工程算例
将可控万向铰接柔性杆与外管的接触模型应用到钻井工程中,对超短半径水平井造斜段柔性钻具进行接触非线性分析。
3.1 柔性钻具力学模型的建立
超短半径水平井造斜段曲率半径为3.2 m,井斜角为90°,选取柔性钻杆和导向筛管为研究对象,柔性钻杆和导向筛管材料均为35CrMo,屈服强度为835 MPa,抗拉强度为980 MPa,弹性模量为210 GPa,泊松比为0.3,密度为7 850 kg/m3。导向筛管的外径为110 mm,内径为95 mm,柔性钻杆与导向筛管的摩擦系数取0.3。
柔性钻杆可控铰接连接部件结构如图5(a)所示,由于研究的重点在于细长柔性钻杆与导向筛管之间的接触状态,并非工具的强度,故为了提高计算效率,考虑柔性钻杆的内部结构,将其简化为相应截面尺寸的圆柱结构,简化后的结构如图5(b)所示。单节柔性钻杆各截面S1~S5对应的长度分别为33、28、38、32和27 mm,对应的外径分别为54、84、84、91和69 mm,内径均为30 mm,铰接位置位于截面S2和截面S3之间。

图5 单节柔性钻杆结构Fig.5 Structure of single flexible drill rod
柔性钻杆及导向筛管均采用梁单元进行离散,柔性钻杆铰接连接采用万向铰单元进行离散,由于单节柔性钻杆有5个不同的截面,因此将单节柔性钻杆划分为5个梁单元,1个万向铰单元,导向筛管的单元长度与柔性钻杆相对应。导向筛管全约束,柔性钻杆上端约束横向线位移,柔性钻杆下端约束线位移和扭转方向的角位移,柔性钻杆与导向筛管之间为接触摩擦边界,柔性钻杆承受自重q和T=2 kN·m的扭矩,柔性钻具力学模型如图6所示。

图6 柔性钻具力学模型Fig.6 Mechanical model of flexible drilling tool
3.2 柔性钻具力学分析
为了研究柔性钻杆中铰接点的影响,给出了无万向铰接和有万向铰接的计算结果,对于有万向铰接的柔性钻杆,又给出了不同铰接转动限制度数的计算结果。柔性钻杆在重力和扭矩作用下发生变形,将柔性钻杆变形放大50倍,得到无铰、铰接处转动限制度数分别为1°、3°和不限制铰接处转动度数的柔性钻杆变形和总位移分别如图7、8所示,柔性钻杆铰接处绕x方向和z方向的转角如图9所示,柔性钻杆与导向筛管的接触压力如图10所示,柔性钻杆的扭矩如图11所示。

图7 柔性钻杆变形Fig.7 Flexible drill rod deformation

图8 柔性钻杆总位移分布Fig.8 Distribution of total displacement of flexible drill rod
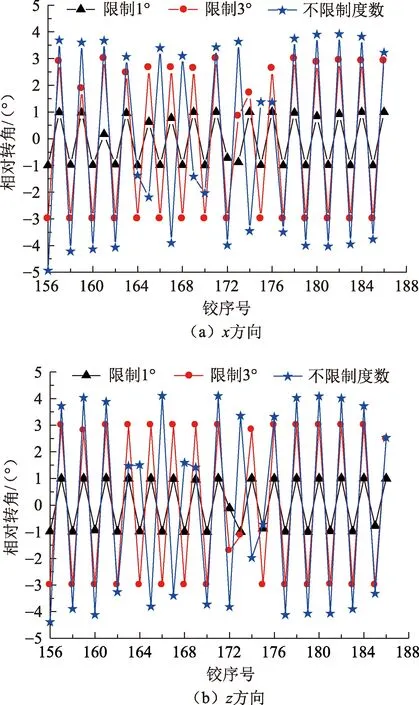
图9 柔性钻杆铰接处转角Fig.9 Angle of hinged joint of flexible drill rod
结合图7~11可知,有铰时,柔性钻杆的变形相对于初始构型呈现“折线形”的变形,随着铰接处转动限制度数的增大,柔性钻杆的平均总位移、相对转角逐渐增大,“折线形”变形趋势越明显;铰接连接的柔性钻杆总位移上下波动较大,随着进尺的增大,单节柔性钻杆相同截面处的位移总体呈减小的趋势,铰接位置处的总位移大于非铰接处。无铰时,柔性钻杆的总位移变化较平稳,且随着进尺的增大,先增大后减小;当铰接处不限制度数时,铰接位置最大转角为5°,这是由于柔性钻杆与导向筛管之间的间隙决定的,当铰接处限制度数为1°和3°时,铰接位置转角多数达到限制度数,柔性钻杆由机构变为结构;柔性钻杆与导向筛管的接触压力随着柔性钻杆铰接处限制度数的增大而增大,只有柔性钻杆最大截面处与导向筛管接触,且接触压力呈随机分布状态;柔性钻杆的扭矩随着铰接处限制度数和进尺的增大而逐渐减小,柔性钻杆扭矩的损失包括两部分,一部分是环向摩擦造成扭矩损失,一部分是万向铰传动轴不在一条直线上,存在一定的夹角,导致扭矩损失,因此在设计柔性钻杆时,应充分考虑万向铰转动限制度数对载荷传递的影响。

图10 接触压力分布Fig.10 Contact pressure distribution
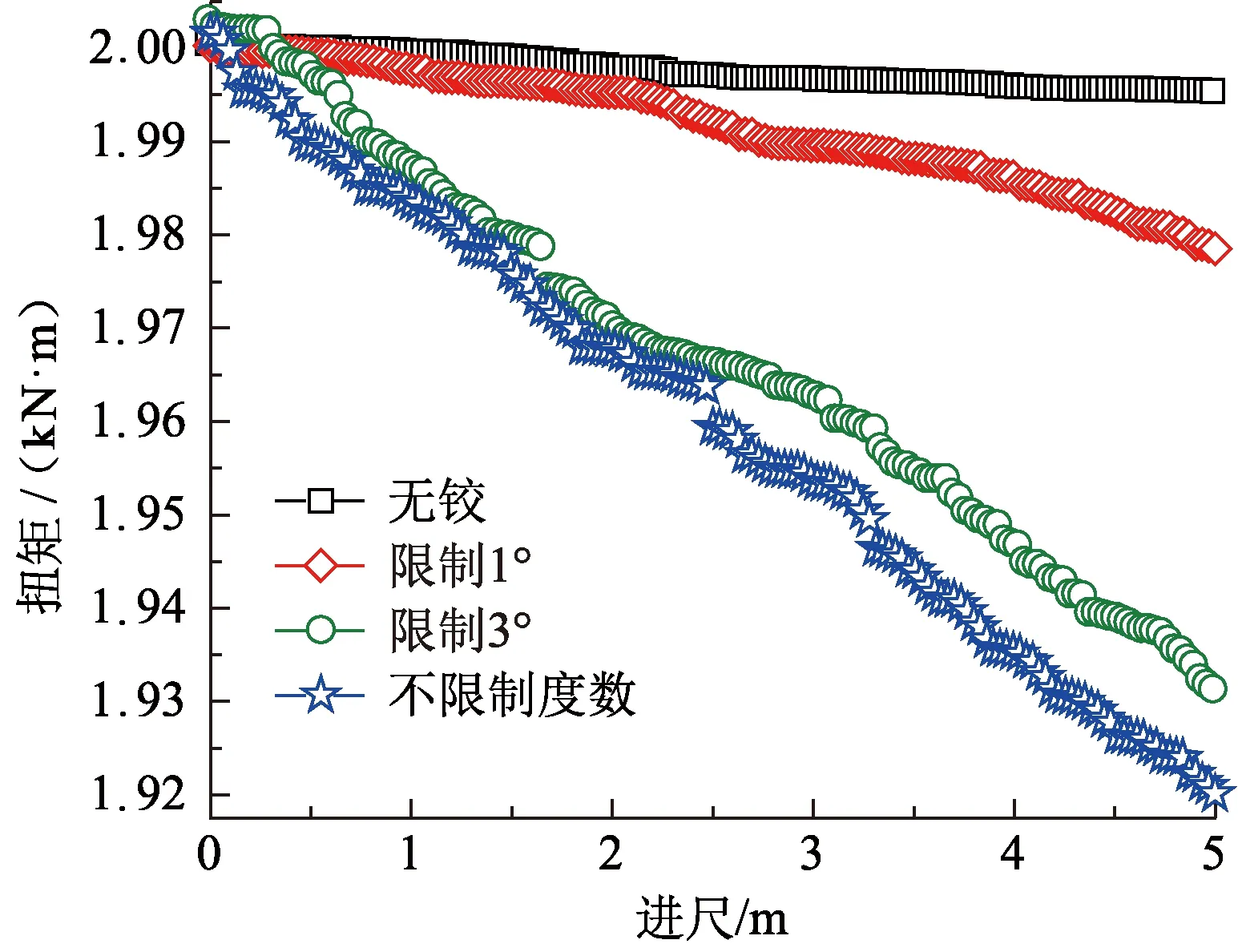
图11 柔性钻杆扭矩分布Fig.11 Torque distribution of flexible drill rod
4 结 论
(1)考虑可控万向铰连接的机构问题及接触非线性问题,将空间梁单元、万向铰单元和接触单元相结合,建立了外管内可控万向铰接柔性杆接触非线性有限元模型,给出了数值计算方法。
(2)典型算例的理论解与数值解十分吻合,最大误差仅为1.08%,说明所建模型和算法具有可行性。
(3)铰接柔性钻杆的变形相对于初始构型呈现“折线形”的变形,随着铰接处转动限制度数的增大,柔性钻杆的平均总位移、相对转角逐渐增大,柔性钻杆与导向筛管的接触压力逐渐增大,接触位置增多,柔性钻杆扭矩逐渐减小,为柔性钻杆的设计和现场施工提供理论指导。
