基于共邻节点相似度的社区划分算法

付立东 郝伟 李丹 李凡

摘 要：复杂网络中的社区结构能帮助人们认识网络的基本结构及其功能。针对目前多数社区划分算法准确率低、复杂度高的问题，提出了一种基于共邻节点相似度的社区划分算法。首先，为了计算节点间相似度值，提出了相似度模型，该模型通过将被测节点对的邻居节点引入一并计算，提高了相似度度量的准确性;然后，计算节点局部影响力值，能客观地表现出节点在所处网络中的重要性;其次，结合节点相似度值和节点局部影响力值对节点进行层次聚类，完成网络社区结构的初步划分;最后，通过聚合初步划分的子社区，获得复杂网络的最优模块度值。仿真结果表明，在网络的社区特征模糊时，与新的基于局部相似度的社区发现算法（CDALS）相比，所提算法的准确率提高了14%，证明了所提提法更能够准确、有效地划分复杂网络的社区结构。

关键词：共邻节点;相似度度量;节点局部影响力;模块度;社区划分

Abstract： The community structure in complex networks can help people recognize basic structure and functions of network. Aiming at the problems of low accuracy and high complexity of most community division algorithms， a community division algorithm based on similarity of common neighbor nodes was proposed. Firstly， a similarity model was proposed in order to calculate the similarity between nodes. In the model， the accuracy of similarity measurement was improved by calculating the tested node pairs and their neighbor nodes together. Secondly， local influence values of nodes were calculated， objectively showing the importances of nodes in the network. Thirdly， the nodes were hierarchically clustered according to the similarity and local influence values of nodes， and preliminary division of network community structure was completed. Finally， the preliminary divided sub-communities were clustered until the optimal modularity value was obtained. The simulation results show that compared with the new Community Detection Algorithm based on Local Similarity （CDALS）， the proposed algorithm has the accuuracy improved by 14%， which proves that the proposed algorithm can divide the community structure of complex networks accurately and effectively.

Key words： common neighbor node; similarity measurement; local influence of node; modularity; community division

0 引言

復杂网络是复杂系统的典型表现形式，得到了经济学、生物学和社会学等不同学科学者的广泛关注，成为当今的热点研究课题[1-2]，而通过网络的社区结构来分析研究网络的功能和特征，已经成为复杂网络的研究趋势。网络的社区结构[3]，是网络中的个体之间按照某种规则而自然形成或人为构造的一种关系，社区结构的特征表现为将网络分割成多个子网络，子网络内部的链接比较紧密，而子网络之间的链接则比较稀疏[4]。

当前在社区网络的定义、发现和识别等方面有许多研究[5-7]。节点间的相似度是复杂网络节点的一个特性，越相似的节点越容易聚集成群、形成社区结构[8]，针对这个特性提出了很多社区划分算法。顾亦然等[9]提出了一种新的基于局部相似度的社区发现算法（a new Community Detection Algorithm based on Local Similarity， CDALS），通过引入节点对及其共同邻居间相互联络的亲密程度，定义了新的相似度指标，基于网络节点相似度矩阵，结合改进的K均值（K-means）聚类方法对网络节点进行相似性聚类，实现网络的社区划分;梁宗文等[10]定义了节点全局和局部相似性衡量指标，将节点按相似性合并条件划分到同一个社区中，待所有节点都被划分到社区中后终止算法，完成网络的社区划分，本文将此算法记为Similarity算法。目前，基于节点相似度的社区划分算法都普遍具有算法复杂度高、准确性较低的问题。针对该问题，本文考虑到节点对与共同邻居节点之间的关系，定义了新的节点相似性度量，利用节点局部影响力和模块度度量作为阈值，进而准确、有效地进行社区划分。

1 相关定义

1.1 相似度模型

以每个网络节点作为背景，结合其所有邻居节点，形成以此节点为核心的星型邻域网络[11]。图1表示无向网络G=（V，E），其中V={v1，v2，…，vn}表示节点的集合，E={（vi，vj）|vi，vj∈V}表示边的集合，用蓝色标记网络G中的节点x和节点y，红色标记节点x和节点y的邻居节点，深黑色标记它们的共同邻居节点。以节点x和节点y分别为核心的星型邻域网络X和星型邻域网络Y如图2所示。

对星型邻域网络中的节点进行描述：

在式（1）中，0表示节点不属于这个星型邻域网络，1表示节点属于这个星型邻域网络。aX，Y表示属于星型邻域网络X且不属于星型邻域网络Y的节点总数，bX，Y表示属于星型邻域网络Y且不属于星型邻域网络X的节点总数;如果cX，Y=0，则表示星型邻域网络X和星型邻域网络Y没有共同邻居节点。

将图2星型邻域网络用图3文氏图来表示。

这里，H（X）表示星型邻域网络X中全部节点集合，H（X|Y）表示属于星型邻域网络X且不属于星型邻域网络Y的节点集合，H（X，Y）表示星型邻域网络X和星型邻域网络Y的全部节点集合，I（X，Y）表示星型邻域网络X和星型邻域网络Y共有的节点集合。

注 在式（3）中，MAX（H（X），H（Y））、12（H（X）+H（Y））、H（X，Y）这三个变量存在的意义是对变量I（X，Y）取值范围进行限定，从作用上来说是等价的，本文不考虑这三个变量间的比较。

基于以上这些基础，对两个星型邻域网络间相互缺少的节点进行数字化度量，例如星型邻域网络Y在星型邻域网络X中缺少的节点，那么网络X中的节点与网络Y中的每一个节点进行匹配，定义如下：

对式（4）中进行匹配的节点i和节点j星型邻域网络化处理，可得：

其中：h（w，z）=w/（z（z-1）/2），w代表两个星型邻域网络中所有节点进行划分后每个星型邻域网络含有的节点个数，z代表两个星型邻域网络包含的节点总数，z（z-1）/2表示为两个星型邻域网络的网络强度。

星型邻域网络X中所有节点再求和，至此得到星型邻域网络Y在星型邻域网络X中缺少的节点度量：

最后对星型邻域网络X进行度量：

其中：w为星型邻域网络X包含的节点总数，z为两个星型邻域网络包含的所有节点数。

同理，对星型邻域网络Y的定义同星型邻域网络X的定义一样。

1.2 共邻节点相似度定义

基于相似度模型，节点x和节点y的相似性度量：

1.3 节点局部影响力

该指标从源节点的最近邻节点和次近邻节点出发，能有效地识别出局部信息下节点的影响力，给定网络中的一个节点i，其局部影响力指标Li定义：

其中：Γi和Πj分为节点i的最近邻节点集合和次近邻节点集合，Nv为节点i的次近邻节点度数。

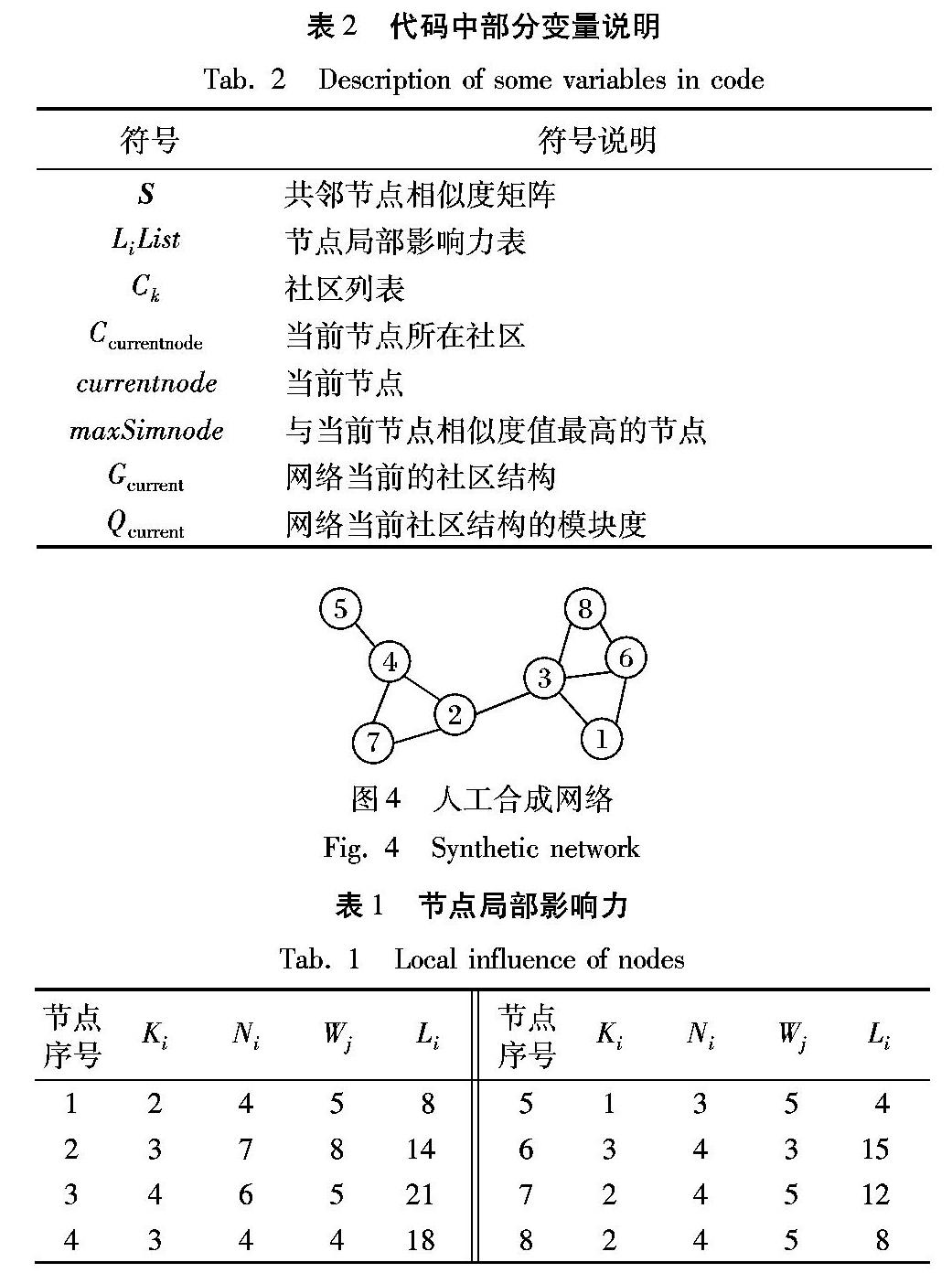
如图4所示，网络包含8个节点，对该网络进行节点局部影响力计算，結果如表1所示。以节点3为例，具体计算方法为：节点3包含4个最近邻节点（1，2，6，8），以及2个次近邻节点（4，7），由式（10）得：w3=5，由式（9）可知节点3的局部影响力L3=w1+w2+w6+w8=21。各节点度值Ki，近邻节点数Ni，次近邻节点度数总和Wj以及节点局部影响力Li如表1所示。

相关研究文献[12]表明，当获取到给定网络的节点影响力集后，对这些节点进行聚类，通常能获得稳定的社区结构。

2 基于共邻节点相似度的社区发现算法

好的社区发现算法应该同时满足两个条件：1）较低的时间复杂度;2）较高的社区划分准确度。然而现有的很多算法难以同时达到以上两点，针对上面两个条件，本文提出了一种新的基于共邻节点相似度的社区发现算法。

2.1 算法改进

本文在计算节点间的相似度值时，计算拥有共同邻居节点的节点对间的相似度，若节点间没有共邻节点，则认为两者相似度为0;若节点间有共邻节点，则两者的相似度取决于共邻节点的数量和共邻节点占邻居节点总数的比重，共邻节点占邻居节点总数比重越大，则两节点间的相似度就越高。基于相似度模型，将式（1）中得到的cX，Y是否等于0作为是否继续计算两个节点相似度的依据：如果cX，Y不等于0，则继续进行相似度值计算;反之，则结束此节点对间的计算，以此来达到降低算法复杂度的目的。

其次，当前大多数局部相似度度量都只关注节点与共同邻居节点间的联系，而忽视除共同邻居节点外其他邻居节点对节点间相似度的贡献，基于此，本文在提出相似度模型时，引入式（4）和（5），将被测节点对的所有邻居节点对节点相似度的作用一并计算，提高了相似度度量的准确性。

最后，针对传统社区发现算法随机选取一个节点作为初始社区，并且将当前节点可能会与多个节点具有相同的相似度时，不能确定选取哪一个节点作为下一个当前节点等特殊情况考虑进去，因此加入节点的局部影响力，在节点进行聚类时加以辅助，以便达到高质量的划分效果。节点影响力可以客观地表现出节点在所处网络中的重要性，而且不会增加算法的时间复杂度，所以它适合用来进行节点聚类。

基于以上因素，这样算法将节点间的相似度度量转化成为星型邻域网络间的相似度度量，在相似度、节点影响力的基础上，本文提出基于共邻节点相似度的社区划分算法。

2.2 算法描述

步骤一 初始社区形成。

1）对给定的网络，按照式（8）获得n*n的共邻节点相似度矩阵S，S={Sij}，n=|V|，其中n为节点数，V为节点集，初始聚类时，将每个节点看作一个独立的社区。

2）根据节点局部影响力表，在节点集V中选取影响力最大的节点i，将其置为当前节点，根据相似度矩阵选取与当前节点i相似度值最高的节点j。V=V-i。