可穿戴设备数值型敏感数据本地差分隐私保护

马方方 刘树波 熊星星 牛晓光

摘 要：针对数据服务器不可信时，直接收集可穿戴设备多维数值型敏感数据有可能存在泄露用户隐私信息的问题，通过引入本地差分隐私模型，提出了一种可穿戴设备数值型敏感数据的个性化隐私保护方案。首先，通过设置隐私预算的阈值区间，用户在区间内设置满足个人隐私需求的隐私预算，同时也满足了个性化本地差分隐私;其次，利用属性安全域将敏感数据进行归一化;最后，利用伯努利分布分组扰动多维数值型敏感数据，并利用属性安全域对扰动结果进行归一化还原。理论分析证明了该算法满足个性化本地差分隐私。实验结果表明该算法的最大相对误差（MRE）明显低于Harmony算法，在保护用户隐私的基础上有效地提高了不可信数据服务器从可穿戴设备收集数据的可用性。

关键词：可穿戴设备;不可信第三方;本地差分隐私;个性化;归一化

Abstract： Focusing on the issue that collecting multi-dimensional numerical sensitive data directly from wearable devices may leak users privacy information when a data server was untrusted， by introducing a local differential privacy model， a personalized local privacy protection scheme for the numerical sensitive data of wearable devices was proposed. Firstly， by setting the privacy budget threshold interval， a users privacy budget within the interval was set to meet the individual privacy needs， which also met the definition of personalized local differential privacy. Then， security domain was used to normalize the sensitive data. Finally， the Bernoulli distribution was used to perturb multi-dimensional numerical data by grouping， and attribute security domain was used to restore the disturbance results. The theoretical analysis shows that the proposed algorithm meets the personalized local differential privacy. The experimental results demonstrate that the proposed algorithm has lower Max Relative Error （MRE） than that of Harmony algorithm， thus effectively improving the utility of aggregated data collecting from wearable devices with the untrusted data server as well as protecting users privacy.

Key words： wearable device; untrusted third-party; local differential privacy; personalization; normalization

0 引言

随着人们对健康越来越重视，以及硬件和通信等技术的飞速发展，各种可穿戴设备进入人们的生活，并成为人们记录监控自身健康的一个重要的部分。服务提供商或者第三方收集可穿戴设备用户[1]的数据并进行统计分析，用于市场分析或者决策制定。可穿戴设备数据指的是与可穿戴设备相关的传感器类型数据、用户设置数据以及设备的绑定信息等，如疾病监测传感器类型数据、监测频率设置、数据限制设置、使用时间、电池容量、设备品牌等，第三方热心于收集这些数据，用于市场分析、新产品开发等决策依据。实际中不存在完全可信的第三方，可穿戴设备与第三方进行数据传输时，会泄露用户数据，攻击者根据获得的用户数据可能推测出用户的敏感信息，比如家庭住址、使用习惯、健康状况等。

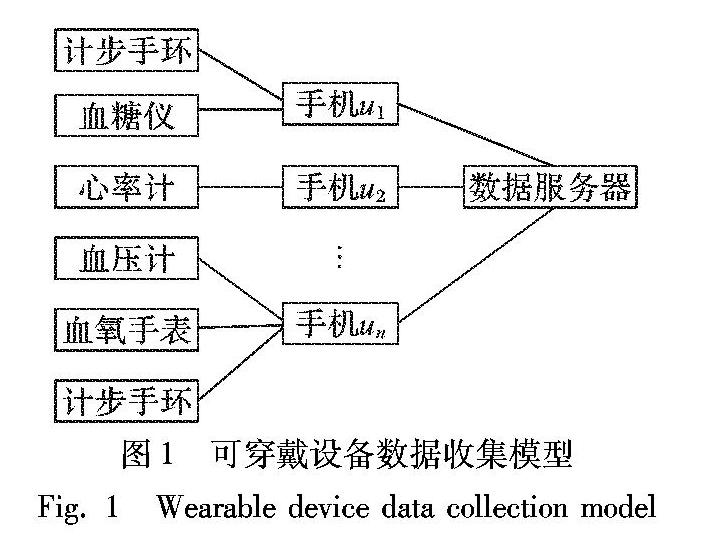
可穿戴设备数据收集模型如图1所示，可穿戴设备包括运动健康型设备（手环）和医疗设备（心率计、血氧手表、血糖仪以及血压计等）。移动设备从可穿戴设备中收集设备数据此处是否应该为数据？需明确，并发送到不可信第三方数据汇聚器中。用户可把穿戴式设备接入移动健康应用程序（mobile Health applications， mHealth），監测自身的健康状况。数据汇聚器Aggregator将通过mHealth收集健康数据，这些数据可为第三方科研机构和企业提供数据服务。例如健康机构收集各个地区人们的每日平均步数，通过和各地区肥胖率对照，分析并获得运动和肥胖率的关系。然而，不可信的数据汇聚器可能从mHealth获得用户的健康数据关联出用户的健康状况。从佩戴的设备类型分析出可能患有某种疾病，这将导致用户的健康状况的隐私泄露。

Facebook数据泄露事件[2]揭露出第三方应用收集和利用数据对用户数据隐私安全的威胁。Papageorgiou等[3]在2018年通过对Google Play上1080个医疗健康移动程序的隐私性和安全性进行分析，发现大部分应用程序向第三方发送用户健康信息，而且无法判定第三方是否被授权，极易造成用户隐私泄露。

第三方数据服务器对可穿戴设备群体用户的收集分析需要隐私保护。有研究者提出差分隐私保护模型，其严格定义了隐私保护的强度，即任意一条记录的添加或者删除，都不会影响最终的查询结果。相比k-匿名、l-多样性等需要特殊攻击假设和背景知识的方法，差分隐私能够抵御背景攻击。而传统的差分隐私模型是中心化，即该模型的前提假设：有可信的第三方数据收集者。在可穿戴设备数据收集分析中，不可能存在完全可信的数据服务器，因此，引入本地差分隐私（Local Differential Privacy， LDP）模型[4-5]对可穿戴设备数据收集进行隐私保护。本地差分隐私的提出是为了防止来自不可信第三方的隐私攻击。本地差分隐私保护模型不允许数据服务器收集用户的真实数据，而是汇聚对真实数据进行扰动后的含噪数据，以保护单个用户的数据隐私安全。第三方对扰动后的数据进行汇聚并求精处理，获得的统计数据即是本地差分隐私保护模型的输出结果。本地差分隐私保护模型的要求是模型既能保证数据的隐私性，又能保证统计结果的可用性。本地差分隐私是通过添加的噪声来实现隐私保护，通过隐私预算来衡量和调节隐私保护程度。在实际应用中，本地差分隐私适用于众包数据的采集[6]等场景。

可穿戴设备敏感数据是多类型的，包括分类型数据和数值型数据等。针对分类型数据的本地差分隐私保护，主要研究频数估计或者計数估计的可用性;针对数值型数据的本地差分隐私保护，主要研究均值估计的可用性。用户敏感数据包含分类型数据和数值型数据，这里我们主要研究其中的多维数值型数据的均值估计，例如可穿戴设备的平均使用时长、电池容量等。现有的多维数值型数据的本地差分隐私算法随着维度的增加，误差增大，不满足可穿戴设备多维数值型敏感数据的可用性要求。

在本地设置中，可穿戴设备用户存在个性化的隐私需求，例如用于医疗监测的可穿戴设备和用于运动健康的可穿戴设备数据敏感程度不同，使用可穿戴医疗设备的健康用户和患病用户，他们对于监测数据的敏感程度不同，因此可穿戴设备的隐私保护框架在用户移动端进行数据扰动处理过程时，用户可以个性化地设置自己的隐私偏好，以达到保护个性化保护用户敏感信息的目的。

综上所述，在可穿戴设备平台中单纯使用本地差分隐私并不能满足用户需求，需要结合可穿戴设备数据特点设计新的本地差分隐私保护方案来对用户进行个性化的隐私保护。本文提出了基于本地差分隐私的可穿戴设备多维数值型敏感数据的个性化隐私保护方案。本文的工作有如下两点：

1）可穿戴设备用户自主设置隐私偏好，个性化保护可穿戴用户的隐私，并且从理论上证明了个性化隐私保护算法满足本地差分隐私算法。

2）研究并分析安全域对多维数值型敏感数据均值估计可用性的影响，并对可穿戴设备多维相互独立的属性在相应安全域内进行独立扰动。

1 相关工作

随着可穿戴设备和健康产业的发展，针对可穿戴设备数据分析的安全和隐私泄露问题受到人们的关注。

移动应用程序向第三方分享可穿戴设备的用户数据会造成用户位置、行为习惯、健康状况、患有某种疾病等信息泄露。针对应用程序分享可穿戴设备数据产生的问题，Raghavan等[7]提出的操作系统级别的移动隐私框架OVERRIDE，允许用户对可穿戴设备数据可能包含的用户隐私信息进行扰动之后再发给应用程序。Kotz等[8]提出移动健康和家庭医疗体系的隐私框架，在这个架构中，出于隐私保护，第三方不被允许收集可穿戴设备数据。

但这些研究没有针对不可信的第三方数据汇聚中心提出具体的隐私保护框架和隐私保护技术。本地差分隐私的提出是防止不可信的第三方服务器数据收集过程中发生隐私泄露。

本地差分隐私的研究目前有分类型数据和数值型数据两个方面。ErlingssonRAPPOR[9]是Google公司提出的本地差分隐私算法，针对字符串进行计数估计，具有误差低、可用性高的特点，但通信开销较大，不适用在可穿戴设备场景中。Bassily等[10]针对分类型属性的频数估计提出了基于随机映射矩阵的S-Hist算法，S-Hist是目前大部分针对分类型属性本地差分隐私保护算法的基础。Nguyen等[11]针对数值型数据和分类型数据提出了Harmony算法，其中针对分类型数据的Harmony-frequency算法适用于属性值域比较大的情况下，但是误差大而且不稳定;针对数值型数据的Harmony-mean算法是目前应用较多的数值型数据均值估计算法，具有可用性高的特点。Wang等[12]也提出了针对分类型数据的OLH（Optimized Local Hashing）请补充OLH的英文全称算法，OLH算法比Harmony-frequency算法误差小、可用性高。目前，本地差分隐私技术在工业界已经得到运用：谷歌公司[9，13]使用该技术从Chrome浏览器采集用户的行为统计数据，例如默认首页、默认搜索引擎等，以了解用户设置中是否存在恶意劫持;苹果公司将该技术应用在操作系统iOS 10上保护用户的设备配置数据，分析群体用户的使用模式，并不会触及用户敏感信息，例如2017年Apple应用本地差分隐私分析和调查网民emoji的使用情况和群体特征;Samsung也提出了相应的本地差分隐私系统[11]，通过手机操作系统绑定的诊断工具来收集绑定的用户信息，不仅能收集分类型数据，例如屏幕分辨率、是否打开定位功能等，还能收集数值型数据，例如内存、使用时间、电池容量等。

针对个性化本地差分隐私算法的研究有Akter等[14]提出的针对一维数值型数据个性化本地差分隐私（Private Estimation of Numeric Aggregates， PENA）算法，PENA算法假设用户集合拥有相同的安全域，在相同安全域上允许用户自由设置自己的隐私预算，但是从理论上来说，PENA算法中的安全域只用于数据归一化处理，并没有降低误差、提高可用性的作用，而且由于可穿戴设备用户敏感数据属于多维数据而且不同属性安全域不同，不能直接应用该算法。Chen等[15]提出个性化的位置数据本地差分隐私（Personalized Count Estimation Protocol， PCEP）算法，但是PCEP算法中使用的S-Hist扰动算法误差比较大并且误差具有随机性，算法的可用性有待提高。

2 本地差分隐私基本概念及相关性质

本章对本文提到的本地差分隐私定义及其实现机制和性质进行概述。

定义1 差分隐私[16]。D和D′是两个相邻数据集，最多有一个元组不同，Δ（D，D′）=1，随机函数算法M：D→Rd，Ran（M）是M在D和D′上的所有可能输出，Ran（M）的任意子集S，如果满足下列不等式，则M满足ε-差分隐私。

其中：Pr表示隐私被披露的风险概率;ε是隐私预算，定义了隐私保护程度，体现了算法M前面交代过M是函数，此处又指算法，二者是否应该统一一下，请明确。若是不同含义，请用另外一个字母来表示算法，不要与其他变量名称再重复了能够提供的隐私保护水平，值越小隐私保护程度越高。

定义2 本地差分隐私[4]。给定n个用户，每个用户对应一条记录，给定一个隐私算法M及其定义域Dom（M）和值域Ran（M），若算法M在任意两条记录t和t′（t，t′∈Dom（M））上得到相同输出结果t*（t*∈Ran（M）），满足下列不等式，则M满足ε-本地差分隐私。

本地差分隐私的实现机制通常是随机响应（Randomized Response， RR）机制[17]。随机响应机制的主要思想是利用用户对敏感问题响应的不确定性对原始敏感數据进行隐私保护，同时估计用户分布。假设属性有两个可能值-1和+1，每个用户以p的概率响应真实ti[Aj]，1-p的概率响应一个随机值，随机值为-1和+1的概率相同，因此，用户ui响应值的期望为p×ti[Aj]。因为要获得一个无偏的估计，所以响应值的缩放因子cε=1/p，即用户ui以p+（1-p）/2的概率响应cε×ti[Aj]，（1-p）/2的概率响应-cε×ti[Aj]。对比用户ui的响应值和真实值，两者相同的概率是p+（1-p）/2，两者不同的概率为（1-p）/2，根据定义2，要满足本地差分隐私，需要p+（1-p）/2（1-p）/2≤eε（e为自然常数）全文中的e，是指自然指数e吗？还是一般的变量名？请明确。回复：在公式后添加描述：e为自然常数，等式成立的条件是p=（eε+1）/（eε-1）。第三方数据汇聚中心聚合所有用户的数据，计算平均值即为属性Aj均值的无偏估计。

定义3 个性化本地差分隐私[14]。用户ui的隐私设置偏好为（τ，εi），对于任意两个输入t和t′，其中t，t′∈τ，任意的输出t*，其中t*∈Dom（M），如果算法M满足下列公式：

则算法M满足（τ，εi）个性化本地差分隐私。

性质1 序列组合性[5]。给定数据集合D和n个隐私算法Mi（1≤i≤t），且Mi（1≤i≤t）满足εi-本地差分隐私，那么Mi（1≤i≤t）在D上的序列组合满足ε-本地差分隐私，其中ε=∑ni=1εi。

性质2 并行组合性[5]。给定数据集合D，将其划分为n个互不相交的子集，D={D1，D2，…，Dn}，设隐私算法M在任意子集上满足ε-本地差分隐私，则算法M在D={D1，D2…，Dn}上的组合运算满足ε-本地差分隐私。

在本地差分隐私中存在两种数据保护框架，即交互式和非交互式框架。交互式框架下，第i个输出依赖于第i个输入以及前i-1个输出;非交互式框架下，第i个输出仅依赖于第i个输入，本文研究非交互式框架下的本地差分隐私。

3 可穿戴设备数据个性化保护方案

3.1 问题描述

下面对可穿戴设备多维数值型敏感数据隐私泄露问题进行描述，并给出隐私汇聚方案的预期实现目标，同时对现有的数值型本地差分隐私算法存在的问题进行分析。

第三方定期收集可穿戴设备的多维数值型敏感数据，用于用户群体使用模式的市场调查和决策制定。在统计数据发布过程中，由于存在不可信的第三方，中心化隐私保护模型的数据收集方式容易被攻击，如果个人敏感数据直接被不可信的第三方服务器获取，则用户的使用习惯、行为爱好甚至健康状况可能被泄露，因此采用本地化隐私保护模型——本地差分隐私对可穿戴设备多维数值型敏感数据进行隐私保护。如表1所示，可穿戴设备相关的数值型敏感属性来源具有多元化的特点，敏感数据可能来源于可穿戴设备、移动设备或者用户输入。对于相同的属性，不同的用户有不同的隐私保护需求;不同的属性，同一个用户有不同的敏感保护级别，在本地差分隐私中引入个性化隐私保护来实现上面两种隐私保护需求。

用户和第三方服务器相互通信，用户首先对多维数据进行扰动，发送给第三方服务器，第三方服务器汇聚所有的数据并进行均值估计。假设可穿戴设备的用户敏感数据包含d维属性，属性之间的关联性已知，根据本地差分隐私的性质2并行组合性可知，相互独立的数据集合满足本地差分隐私的并行组合性质。

问题描述：假设数值型属性集合A={A1，A2，…，Ad}，属性之间相互独立，用户集合U={u1，u2，…，un}，其中属性个数为d，用户个数为n，全部隐私预算为ε，用户ui的隐私预算为εi，属性的安全域集合Γ={τ1，τ2，…，τd}，τj， j∈d是用户可以公开的属性Aj的数值最小安全范围，εi是限制攻击者在安全域τj范围内区分任意两个数值的能力。隐私保护目标：基于可穿戴设备个性化的隐私需求，满足用户的隐私偏好，在不知道每个用户精确数值的前提下，获取每个属性的均值估计，在保证用户隐私的前提下，保证均值估计的可用性。

目前基于本地差分隐私的均值估计研究较少，主要是针对频数估计的研究。文献中均值估计的算法运用比较多的MeanEst[4]算法和Harmony算法。其中Harmony算法在通信代价、发布误差以及时间复杂度上都优于MeanEst算法，所以3.2节所提出的方案在Harmony算法的基础上进行改进，并且在3.3节从算法的可用性角度对所提方案进行分析。

Harmony是针对多维数值型数据均值估计的算法，由文献[11]可知，最大绝对误差（Max Absolute Error， MAE）为Ο（d log （d）/（εn）），即

其中：X[Aj]是真实均值，Z[Aj]是扰动后的均值， β公式没有看到β，是否遗漏了，需明确。回复：删除该句“β时误差范围的置信度”，已默认β为1是误差范围的置信度。由公式可知，MAE随着属性个数d的增长而增长，因此Harmony不满足高维数据均值估计的可用性要求。由图2可知，当固定隱私预算的取值时，随着属性个数d的增长，相对误差增长的速度很快。

3.2 方案描述

不可信第三方收集可穿戴设备与用户相关的敏感数据，不同设备的属性之间是独立的，不同数据来源的属性之间也是独立的，在本方案中，用户对这些相互独立的属性进行独立扰动，同时用户根据自身敏感性和对属性的敏感性设置自己的隐私偏好。

可穿戴设备多维数值型敏感数据个性化隐私保护方案流程如下：不可信第三方服务器向可穿戴设备用户端发送整体的隐私预算ε，用来约束用户的隐私预算εi。在可穿戴设备用户端，对多维数值型属性分别设置安全域Γ={τ1，τ2，…，τd}和隐私预算εi，其中要保证ε/d≤εi≤ε，i∈n此处的小写n，是否应该为大写N，表示自然数？请明确。回复：n为用户个数，在问题描述中有介绍。使用属性安全域τj对属性Aj的数值进行归一化处理，把数值归一化到[-1，1]区间。由于用户可以设置自己的隐私预算εi，根据ε-LDP的定义，为了保证算法满足ε-LDP，εi需要小于或等于整体隐私预算ε，在3.3节隐私性分析进行详细的证明;同时为了保证可用性，εi需要大于或等于ε/d，这一点在3.3节可用性的分析中也有说明，因此引入权重因子ωi（1/d≤ωi≤1），得到εi=ωi·ε。对属性Aj进行归一化之后，采用随机响应算法LRR随机响应（Local Random Response， LRR）算法对其数据进行扰动。不可信第三方服务器端获取到扰动后的数据，进行均值统计，最后进行归一化还原操作。

算法2的第1）行到第6）行在用户端执行，第7）行和第8）没有第8行，是遗漏了，还是表述错误？请调整。回复：原文：“第7）行和第8）行在服务器执行”，改为“第7）行在服务器端执行”;行在服务器端执行。第2）行到第4）行，用户ui在每个独立属性上做随机响应LRR扰动。第5）行用户ui把d个属性的扰动值发送给服务器server。第7）行服务器server汇聚所有用户发送的扰动数据，分别对每个属性的数据进行均值计算。第8）行服务器进行数据归一化还原操作，并且进行数据归一化还原操作原文：“。第8）行服务器进行数据归一化还原操作”，改为“，并且进行数据归一化还原操作”，获得最终的均值估计结果。

由文献[11]可知，Harmony均值估计算法的最大绝对误差渐近边界是Ο（d log （d）/（εn）），单个属性独立扰动下的最大绝对误差渐进边界是Ο（log （d）/（εn））。由于用户的隐私预算由用户自己设置，所以PLPS的最大绝对误差的渐近边界是Ο（log （d）/（mini∈[n] εin）），当mini∈[n] εi=ε/d时，PLPS的最大绝对误差渐进边界为Ο（d log （d）/（εn））。

4 实验结果与分析

1）属性个数对可用性的影响。

为了研究属性个数对可用性的影响，随机生成虚拟数据集，用户100000个，属性个数取值范围是[4，8，16，20，24，28]，ε=0.5，每个用户随机生成在[ε/d，ε]区间的值作为自己的隐私预算。如图3所示，Harmony算法的相对误差随属性的增长变化很快，PLPS算法MRE随属性个数变化不明显，引入的误差低，提高了可用性。

2）隐私预算对可用性的影响。

实验数据集采用IPUMS的GLOBAL HEALTH数据集（https：//www.ipums.org/），选取100000条用户记录，包含20个数值型属性。ε的取值范围设置为[0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1.0]。在PLPS算法中用户个性化设置自己的隐私预算εi，且需满足条件εi=ωi·ε，1≤i≤n，1/d≤ωi≤1。如图4（a）所示，PLPS算法的最大相对误差MRE比Harmony的最大相对误差MRE小。PLPS算法多维属性在定义的安全域内分别进行归一化处理，每个属性进行单独扰动，比Harmony算法的信息损失率小，同时算法添加的噪声随机性减弱，可用性变高。

为了证明算法PLPS在Harmony算法进行分组扰动后，依然能够保持最大相对误差小的优势，对Harmony算法进行了分组扰动实验。把从GLOBAL HEALTH数据集中选取的属性分成k组，每组内分别进行Harmony扰动，取所有组的最大相对误差中的最大值作为Harmony分组扰动的最大相对误差结果;PLPS算法相当于把属性分为d组，d为全部属性的个数。如图4（b）所示，全部属性个数是20个，k的取值范围是[4，10]，从图中可以看出，增加了个性化隐私的PLPS有效地降低了误差。

5 结语

为了当不可信数据服务器收集可穿戴设备敏感数据时，保护用户隐私信息不被泄露，本文提出了基于本地差分隐私的可穿戴设备多维数值型敏感数据的个性化隐私保护方案：考虑可穿戴设备用户的个性化隐私需求，支持用户自定义隐私偏好;针对属性维度增长对均值估计可用性的影响，采用在属性安全域内独立扰动属性的策略，细化属性的扰动区域。实验结果表明，本文提出的方案有效降低了整体引入的噪声，提高了均值估计的可用性。

本文提出的个性化隐私保护方案考虑的只是数值型数据，并没有对分类型数据或者复杂数据类型进行研究，下一步将对此作更加深入的研究。

参考文献 （References）

[1] 郑增威，杜俊杰，霍梅梅，等.基于可穿戴传感器的人体活动识别研究综述[J].计算机应用，2018，38（5）：1223-1229.（ZHENG Z W， DU J J， HUO M M， et al. Review of human activity recognition based on wearable sensors[J]. Journal of Computer Applications， 2018， 38（5）： 1223-1229.）

[2] 魏书音.从Facebook数据泄露事件看网络运营者对第三方应用的安全管理责任[J].网络空间安全，2018，9（3）：43-46.（WEI S Y. Analyze network operators responsibility for security management of third-party applications from the Facebook data breach [J]. Information Security and Technology， 2018， 9（3）： 43-46.）

[3] PAPAGEORGIOU A， STRIGKOS M， POLITOU E， et al. Security and privacy analysis of mobile health applications： the alarming state of practice[J]. IEEE Access， 2018， 6（99）： 9390-9403.

[4] DUCHI J C， JORDAN M I， WAINWRIGHT M J. Local privacy and statistical minimax rates [C]// Proceedings of the 2013 54th Annual IEEE Symposium on Foundations of Computer Science. Piscataway， NJ： IEEE， 2013： 429-438.

[5] 葉青青，孟小峰，朱敏杰，等.本地化差分隐私研究综述[J].软件学报，2018，29（7）：1981-2005.（YE Q Q， MENG X F， ZHU M J， et al. Survey on local differential privacy[J]. Journal of Software， 2018， 29（7）： 1981-2005.）

[6] 霍峥，张坤，贺萍.满足本地化差分隐私的众包位置数据采集[J].计算机应用，2019，39（3）：763-768.（HUO Z， ZHANG K， HE P. Local differentially private spatial data crowdsourcing[J]. Journal of Computer Applications， 2019， 39（3）： 763-768.）

[7] RAGHAVAN K R， CHAKRABORTY S， SRIVASTAVA M， et al. OVERRIDE： a mobile privacy framework for context-driven perturbation and synthesis of sensor data streams[C]// Proceedings of the 2012 International Workshop on Sensing Applications on Mobile Phones. New York： ACM， 2012： Article No. 2.

[8] KOTZ D， AVANCHA S， BAXI A. A privacy framework for mobile health and home-care systems[C]// Proceedings of the 2009 Workshop on Security and Privacy in Medical and Home-Care Systems. New York： ACM， 2009： 1-12.

[9] ERLINGSSON U， PIHUR V， KOROLOVA A. RAPPOR： randomized aggregatable privacy-preserving ordinal response[C]// Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security. New York： ACM， 2014： 1054-1067.

[10] BASSILY R， SMITH A. Local， private， efficient protocols for succinct histograms[C]// Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing. New York： ACM， 2015： 127-135.

[11] NGUYEN T T， XIAO X， YANG Y， et al. Collecting and analyzing data from smart device users with local differential privacy[J]. ArXiv Preprint，  2016， 2016： 1606.05053.

[12] WANG T， BLOCKI J， LI N， et al. Optimizing locally differentially private protocols[J]. ArXiv Preprint， 2017， 2017： 1705.04421.

[13] FANTI G， PIHUR V， ERLINGSSON U. Building a RAPPOR with the unknown： Privacy-preserving learning of associations and data dictionaries[J]. ArXiv Preprint， 2016， 2016： 1503.01214.

[14] AKTER M， HASHEM T. Computing aggregates over numeric data with personalized local differential privacy[C]// Proceedings of the 2017 Australasian Conference on Information Security and Privacy. Berlin： Springer， 2017： 249-260.

[15] CHEN R， LI H， QIN A K， et al. Private spatial data aggregation in the local setting[C]// Proceedings of the 2016 IEEE International Conference on Data Engineering. Piscataway， NJ： IEEE， 2016： 289-300.

[16] DWORK C， LEI J. Differential privacy and robust statistics[C]// Proceedings of the Forty-first Annual ACM Symposium on Theory of Computing. New York： ACM， 2009： 371-380.

[17] WARNER S L. Randomized response： a survey technique for eliminating evasive answer bias [J]. Journal of the American Statistical Association， 1965， 60（309）： 63-69.