杨氏干涉实验条纹的三维分布及仿真研究

朱孝辉

摘  要：根据杨氏干涉实验的基本原理，在未经任何理论近似的情况下，推导出明、暗干涉条纹所满足的数学方程，并指出干涉条纹空间分布是一族双叶旋转双曲面。在数学方程的基础上，设置实际实验参数，利用Mathematica 12科学计算软件对干涉条纹的三维空间分布进行仿真。通过改变观察屏的位置使屏上得到不同形状的干涉条纹，对屏上干涉条纹的分析与传统光学理论吻合的很好。对干涉条纹三维分布的仿真模拟可进一步加深对杨氏干涉的认识与理解。

关键词：杨氏干涉实验;Mathematica;计算机仿真

中图分类号：O436         文献标志码：A         文章编号：2095-2945（2019）23-0030-04

Abstract： According to the basic principle of Young's interference experiment， without any theoretical approximation， the mathematical equations satisfied by bright and dark interference fringes are deduced， and it is pointed out that the spatial distribution of interference fringes is a family of hyperboloid rotating hyperboloid. Based on the mathematical equation， the actual experimental parameters are set， and the three-dimensional spatial distribution of interference fringes is simulated by using Mathematica 12 scientific calculation software. By changing the position of the observation screen， the interference fringes of different shapes are obtained on the screen， and the analysis of the interference fringes on the screen is in good agreement with the traditional optical theory. The simulation of the three-dimensional distribution of interference fringes can further deepen the understanding and understanding of Young's interference.

Keywords： Young's interference experiment; Mathematica; computer simulation

引言

1802年，英國物理学家托马斯·杨在研究人眼对颜色视觉效应时，想出来一个巧妙的实验方法，演示了光的干涉现象，为光的波动学说提供了坚实的实验基础[1，3]。这个实验方法就是杨氏干涉实验，又名杨氏双缝干涉实验，是大学物理实验中的重要实验之一，其实验思想在近代物理实验中也发挥了重要作用。但是大多数教材及相关文献资料仅给出了实验的相关原理和干涉条纹的二维分布，很少有进一步讨论干涉条纹的三维空间分布。又因为该实验对实验仪器和环境有特定的要求，必须要在相关专业实验室内进行实验。因此本文将推导出干涉条纹的三维分布数学表达式，通过具体实例利用科学计算软件Mathematica 12对杨氏干涉实验条纹进行三维仿真模拟，讨论观察屏上条纹随观察屏位置不同而产生的变化。这必将有利于更加全面的认识杨氏干涉实验及干涉条纹的分布情况。

1 杨氏干涉实验

1.1 实验原理简述

杨氏干涉实验是利用分波前法产生干涉的最著名的例子。经典实验装置如图1所示，光源发出的光通过小孔S照射在光屏A上的两个相距为d的对称小孔S1、S2上，分出的两束相干光波在空间传播时产生相干叠加，在距离为D的观察屏E上形成一定的干涉条纹图样[2]。

1.2 干涉条纹公式推导

干涉条纹实质上就是屏幕与等光程差点的空间轨迹的交线[2]，因此可借助等光程差点的空间轨迹来研究干涉条纹的三维空间分布，且认为空间轨迹与干涉条纹的概念在本文中基本等价。

假设光源为单色点光源，传播介质为空气。为确定干涉条纹的空间分布，如图2所示，选取直角坐标系O-xyz，坐标系原点为小孔S1、S2对称中心，x轴方向为S1、S2连线方向，与x轴垂直且竖直向上的方向为y轴方向。

2 Mathematica仿真过程

2.1 参数选择及仿真模拟

前面已经指出，m不为零时，两点光源干涉的等光程差点在空间的轨迹是双叶旋转双曲面。现考虑实际杨氏干涉实验情况，光波波长？姿取值在3.9×10-4mm-7.8×10-4mm，双缝宽度d取值一般在0.1mm-1mm。在典型情况下[2]，取d=0.2mm，波长不妨取？姿=5.5×10-4mm。当干涉级次m依次取值1到5时通过Mathematica计算可得到此时的双曲面方程为：

（8）

从表达式的值可看出，x2的系数比y2+z2大很多，最小也相差500多倍。这是由于式（6）的形式所决定的，式（6）中波长与缝宽相差4到5个数量级且干涉级m取值一般不大，这必然导致x2和y2+z2项系数相差很多。由立体几何知识可知，x2的系数越大，则双曲面底部越靠近x=0的平面，y2+z2的系数越小，双曲面弯曲程度越小。即在x=0平面附近区域内双曲面是非常“平坦”的，几乎为一个个平面。式（8）中方程的图像亦可由Mathematica画出如图3。

值得注意的是，图3中双曲面及很多书籍和文献中所画的双曲面都仅仅是示意图，它们的坐标轴各比例并不是完全相同的。实际的图像比例应如图4所示，图中双曲面成为紧紧靠近x=0平面的一族平面，这与前面从数学公式上的分析结果是一致的。

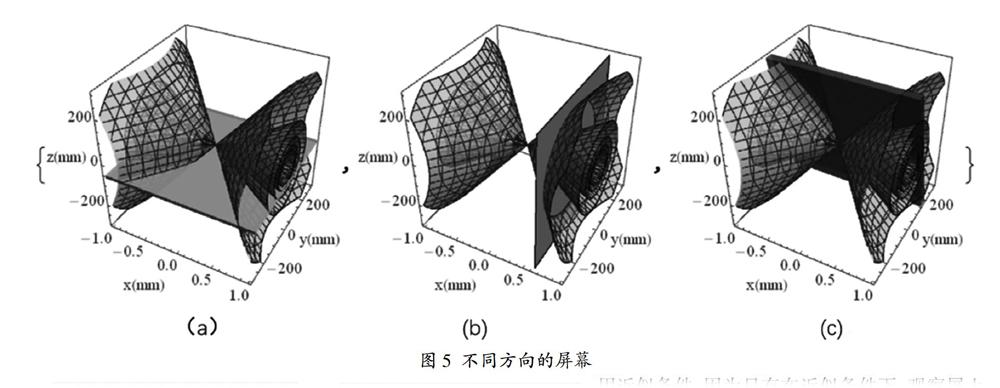
但是为了方便观察分析，依然采用图3中图像比例进行研究，这并不会对研究结果产生实质性影响。由于在观察屏上看到的条纹就是双曲面与屏幕的交线。那么将屏幕设置在不同方向上，将得到不同的干涉条纹。图5中与双曲面相交的不同平面即代表不同方向的观察屏。下面将进一步分析不同位置屏幕上的干涉条纹。

2.2 观察屏垂直于z轴

当观察屏垂直z轴（如图5（a））时，设屏与z=0平面的距离L，这是杨氏干涉实验常规放置屏幕的方式。图6是利用Mathematica画出不同L值时屏与双曲面的交线。

2.3 观察屏垂直于x轴

当观察屏垂直于x轴（如图5（b））时，设屏与x=0平面的距离为H，图7是利用Mathematica画出不同H值时屏与双曲面的交线。

2.4 观察屏在其它位置

当观察屏不与坐标轴垂直时，屏与双曲面的交线随屏位置的不同有很大变化，也即干涉条纹会有不同的变化，但不难想象，条纹形状仍为双曲线或近似直线，只不过条纹间距会有所不同。例如图8中表示观察屏处于x-3z=0的平面上时，其上的条纹分布在y-z平面上的投影图。

3 结束语

本文根据杨氏干涉实验的原理，在没有采用任何近似条件的情况下，推导出干涉条纹三维分布的数学表达式。利用Mathematica画出了明条纹的三维图形，直观的表现出干涉条纹的三维分布情况。并且根据观察屏相对于双孔不同位置，分析了屏幕上条纹的变化情况。借助于仿真图像的分析与相关光学理论结果十分吻合。创新之处在于，不仅利用Mathematica强大的绘图功能仿真了干涉条纹的三维分布，而且与实际相结合，所选用的参数以及由此计算出的曲面方程都是有实际意义的，仿真结果完全可以作为杨氏干涉相关实验的参考与指导。

结合相关物理教材关于杨氏干涉理论分析中的近似处理和条纹分布推导可知，一般物理教材是本文仿真中的一种特定条件下的情况（L？垌d，且观察范围不大）[5]。但是本文只是条纹三维分布做了直观的仿真与简要分析，并没有详细分析屏幕在任意位置时屏上条纹分布及强度和宽度随各参数的变化规律。而一般物理教材中则详细讨论了条纹的变化规律。因此将本文与一般物理教材相关内容结合，可对杨氏干涉实验及其条纹分布具有更加全面深入的认识。

参考文献：

[1]王高亮，孟明，王强.基于Mathematica的杨氏双缝干涉实验仿真[J].周口师范学院学报，2018，35（05）：47-49.

[2]梁铨廷.物理光學[M].电子工业出版社，2012.

[3]赵近芳，王登龙，等.大学物理学（第4版）（下）[M].北京邮电大学出版社，2014.

[4]何坤娜，韩萍，朱世秋，等.杨氏双缝干涉图样的理论模拟[J].物理通报，2016（3）：25-28.

[5]何坤娜，黄坚.杨氏双缝干涉条纹的空间分布及理论模拟[J].物理与工程，2016，26（5）：12-15.

[6]吴玉泉.对“杨氏双缝干涉实验”典型佯谬讨论[J].中学物理教学参考，2003，32（4）：18-19.