轮轨接触面损伤时冲击力作用下热弹塑性分析

李文全

摘  要：轮轨接触面发生剥离断裂等损伤时轮轨冲击力是无损伤时的数倍，不同损伤，不同速度，不同环境温度，轮轨冲击区域温度不同。由于轮轨损伤而产生的极大的轮轨冲击力导致损伤部位应力应变极大，损伤部位温度升高，损伤附近更容易发生较大的弹/塑性变形，使损伤发生扩展。

关键词：踏面损伤;轨面损伤;温度场;轮轨冲击力;应力

中图分类号：U213.42       文献标志码：A         文章编号：2095-2945（2019）23-0001-05

Abstract： When the wheel-rail contact surface is damaged such as peeling fracture， the impact force of wheel-rail is several times higher than that without damage. With different damages， different speeds， different ambient temperatures， the temperatures of wheel-rail impact area are different. Due to the great wheel-rail impact force caused by wheel-rail damage， the stress and strain of the damaged site is very large， the temperature of the damaged site is increased， and the larger elastic/plastic deformation is more likely to occur near the damage， which makes the damage spread.

Keywords： tread damage; rail surface damage; temperature field; wheel-rail impact force; stress

引言

輪轨接触研究是现有铁路研究中的重点之一。在铁路车辆运行中，由于紧急制动擦伤、轮轨疲劳损伤剥离掉块、表层材料塑性流变、材料制作工艺不成熟引起的材料性质不均匀等导致的轮轨接触面损伤会加大轮轨接触力，而较大的轮轨接触力加剧车轮踏面及轨面损伤，形成恶性循环。研究轮轨接触面在损伤情况下的轮轨冲击时应力应变及温度变化对铁路车辆运营与维护有着极其重要的意义。

目前国内外学者对轮轨接触面损伤情况下轮轨力进行了大量分析研究[1-5]，主要集中在踏面或轨道损伤情况下轮轨接触力与损伤长度的关系方面。现有方法大多是通过动力学方法模拟研究轮轨接触面损伤时的轮轨接触力。轨道损伤时，将损伤深度与轨道不平顺耦合;车轮踏面损伤时，将车轮踏面损伤等效为轨道损伤，或根据损伤位置车轮半径相对与未损伤位置的减小量，改变踏面损伤位置车轮半径从而模拟踏面损伤。轮轨接触面出现损伤时，轮轨接触力会在滚过损伤时增大2～3倍，损伤较大时甚至能达到5～6倍。此冲击力远超轮轨设计标准限值，对轮轨伤害极大。

对轮轨滚动接触应力应变情况通过数值方法或有限元方法建立二维理论模型或三维实体模型进行研究[6-8]，结果显示车轮经过踏面损伤部位时，轮轨接触应力变化较大，远超材料屈服极限，将产生较大的塑性变形。现有研究对损伤位置进行热弹塑性分析[9-11]，结果显示轮轨间做纯滑动时或轮轨接触经过损伤位置时，轮轨接触区温度变化较大，应力应变情况与不考虑热应力时差别较大。

现有研究多是从理论分析角度出发对轮轨损伤时温度-应力应变情况进行分析，车轮和轨道简化成圆柱体和长方体，轮轨间进行纯滑动等。本文通过动力学软件对某型动车建立动力学模型，通过设置车轮/轨道接触表面损伤，得出轮轨接触冲击力谱。通过多物理场有限元仿真软件建立轮对-轨道三维实体模型，运用多物理场耦合方法，对轮轨损伤时接触区温度、应力、应变等情况进行研究。

1 模型的建立

1.1 动力学模型

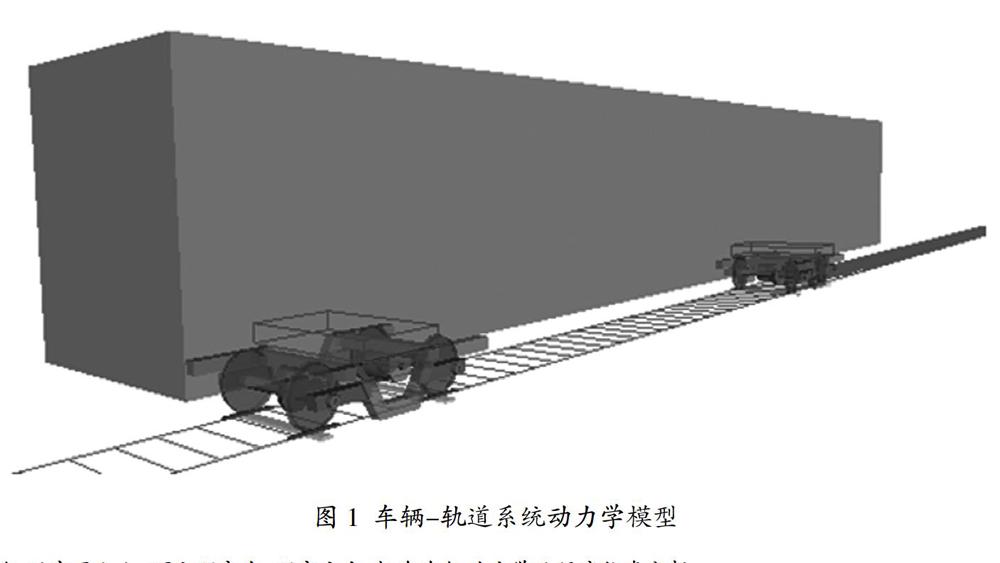
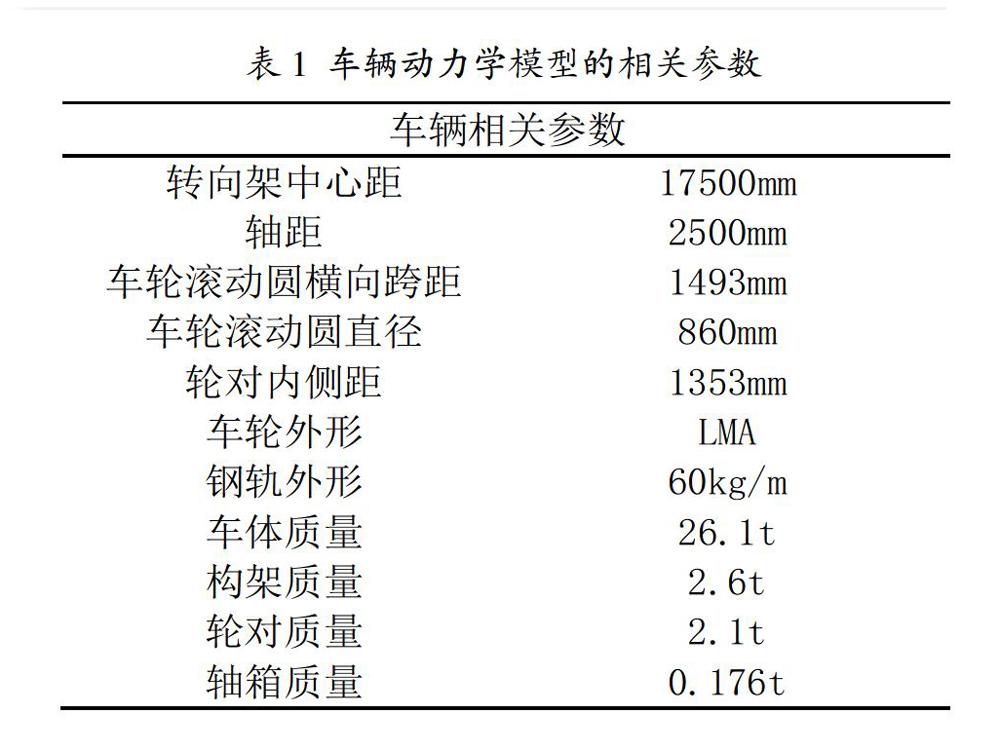
根据某型动车相关参数建立动力学模型，主要参数如表1所示。模型中采用多刚体组合结构，车体、构架、轮对保留6自由度，轴箱仅保留转动自由度，模型如图1所示。其中车轮踏面导入绘制好的LMA踏面，轨面导入60kg/m钢轨轨型。车轮踏面损伤长度按圆周方向测量，轨道轨面损伤长度按照轨道纵向测量，在动力学模型中设置不同的损伤长度，模拟研究轮轨踏面损伤时的轮轨冲击力，并生成时变的轮轨冲击力谱。其中损伤长度与损伤深度关系采用扁疤计算公式[1]：

f（x）=d/2[1-cos（2πx/L）]  d=L2/16R （1）

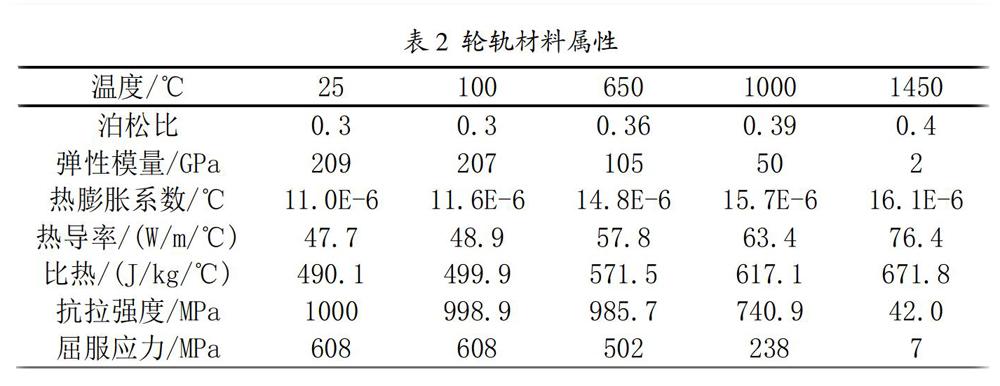
其中x为损伤部位上某一点位置，0

1.2 有限元模型

按照相关标准绘制LMA踏面高速动车车轮、60kg/m轨道及对应车轴模型，轨底坡为1：40，由于模型关于车轴中心面对称，采用半轴模型对称约束边界，模型如图2所示。本文主要研究踏面及轨面的热弹塑性，因此忽略车轮辐板孔车轴制动盘座等结构。将动力学模拟得出的不同长度损伤下轮轨冲击力谱导入有限元软件，并将此载荷施加在半轮轴轨道模型上。

热分析中轮轨接触区热边界条件为：

-λ？坠T/？坠Z=q         （2）

其中λ为材料热导率，Z为接触区温度梯度方向位移。

轮轨材料采用非线性本构关系，轮轨泊松比弹性模量等参数与材料温度相关，参考文献[12]，轮轨材料属性如表2所示。

2 计算分析

2.1 动力学模型计算及结果分析

《高速试验列车动力车强度及动力学性能规范》（95J01-L）规定轮轨垂向力峰值不得超过170kN。在200km/h车速下，车轮踏面出现20mm长扁疤损伤滚过平直轨道时产生的轮轨冲击力P随时间t变化图如3所示。当车轮滚过损伤位置时，轮轨力出现从Q1先减小到Q2后迅速增大Q3的剧烈变化，轮轨力达到最大值后呈现波形衰减。Q1、Q2对应位置为损伤前中侧，Q3对应位置为损伤后侧。

图4所示为平直轨道轨面出现按照公式（1）给定的损伤长度深度公式设置的20mm损伤时，损伤深度H/轮轨冲击力P-轨道位置x关系。由图可知当无损伤车轮滚过存在损伤的轨面时，轮轨冲击力变化剧烈，轮轨力先急剧增大后迅速减小再增大，呈现波形衰减趋势。在出现不同长度的车轮踏面/轨道轨面损伤时，车轮在京津实测轨道谱线路上以200km/h速度运行，将踏面/轨面损伤与轨道谱耦合。轮轨力计算结果如图5所示，随着车轮踏面/轨道轨面损伤长度的增加，轮轨冲击力成倍增长。这对车轮及轨道结构安全性可靠性及相关结构件使用寿命影响极大。

2.2 有限元计算及结果分析

2.2.1 单次冲击模拟

由于损伤过大时轮轨力将超过《高速试验列车动力车强度及动力学性能规范》（95J01-L）中轮轨垂向力170kN的限定值，在实际运用中已达到旋修标准不会长期存在，因此以下主要研究损伤长度为10mm/20mm情况。将动力学轮轨力计算结果进行分析处理，不考虑速度对轮轨冲击力大小的影响，仅考虑速度对冲击频率及作用时间的影响。设定有限元分析几种工况如表3所示。

设置初始环境温度为20℃。将对应轮轨冲击力及作用时间输入有限元模型中进行有限元分析。对有限元模型进行不同工况下单次损伤冲击的瞬态分析，当轮轨接触区温度和应力达到最高点时，轮轨接触区截面温度及应力情况分布相近，温度分布云图如图6所示，由表4及图6可知，轮轨间接触区温度较为接近温度最高点主要分布在轮轨接触表面，因此单次冲击后轮轨的最高温度相同。von Mises应力分布云图如图7所示，应力最大位置并非在接触表面，而是在接触表面下层2mm左右的位置，且相比于轨道，车轮内部应力更大。表4为表3所示四种工况下车轮最高温度、最大应力的具体数值。较大的冲击力作用下，车轮最大应力大于表2中对应温度下的材料屈服应力，会发生塑性变形。

圖8为表3对应编号的四种工况下，接触区最高温度T随时间t变化图。由图可知，经过极短时间的轮轨力冲击，轮轨接触区温度变化极快，单次冲击后温升可达3℃，温度升至最高点后，热量从温度最高区域扩散，温度开始下降。极短的冲击时间内极大的冲击力作用下，冲击力产生的变形不充分。相同冲击力下，作用时间更长的的温升更大（Ta>Tb，Tc>Td）;相同的作用时间下，冲击力大的温升更大（Td>Ta）。

2.2.2 连续冲击模拟

通过动力学分析结果可知单次冲击力与冲击力作用距离。轮对存在20mm长损伤时轮轨力与轮轨力作用距离关系如图9所示。通过运用样条插值及梯形公式将冲击力与作用距离进行积分可知单次冲击功。20mm长损伤冲击的单次冲击功为9J，在不考虑速度对冲击力的影响情况下，速度越快，每秒冲击次数越多，冲击产生功率越大。当车轮踏面出现20mm损伤时，200km/h速度下，每秒车轮转数约20次，冲击功率为180W;当轨道轨面出现20mm损伤时，考虑不同车型的火车以200km/h速度通过时，损伤位置每秒约通过9个车轮，冲击功率约为81W。分别对车轮损伤及轨道损伤两种情况进行模拟。模拟结果如图10所示。当车轮损伤时车轮温升大于轨道损伤时轨道的温升，且温度经过一定的冲击次数后上升速度减慢。

3 结论

通过对轮轨接触位置设置损伤，运用动力学及有限元多物理场耦合的方法，对轮轨接触区冲击力-温度-应力进行研究，得出以下结论：

（1）车轮滚过车轮踏面或轨道轨面损伤位置时，轮轨力变化较大，可达到未损伤位置轮轨力的2～5倍，且冲击力多分布在损伤后侧，使损伤易于向后发展。

（2）较大的轮轨冲击力会引起冲击热效应，使损伤位置附近温度较高。这对损伤位置的材料性能是较大的考验。

（3）当损伤长度大于等于10mm时，轮轨接触区应力较大，已超过材料的屈服极限，损伤会随着车辆运行继续向后扩展。

参考文献：

[1]Newton S G， Clark R A. An investigation into the dynamic effects on the track of wheelflats on railway vehicles[J]. ARCHIVE Journal of Mechanical Engineering Science 1959-1982（vols 1-23），1919，21（21）：287-297.

[2]Rao VDukkipati， RenguangDong. Impact Loads due to Wheel Flats and Shells[J].Vehicle System Dynamics， 1999，31（1）：1-22.

[3]翟婉明.铁路车轮扁疤的动力学效应[J].铁道车辆，1994，32（7）：1-5.

[4]王晨，王旭，罗世辉，等.轮对扁疤对高速列车转向架振动特性的影响[J].中国机械工程，2017，28（2）：246-251.

[5]王忆佳，曾京，高浩，等.车轮扁疤引起的轮轨冲击分析[J].西南交通大学学报，2014，49（4）：700-705.

[6]蔡武，温泽峰，金学松.钢轨接头轨缝对轮轨接触应力的影响[J].工程力学，2006，23（9）：173-178.

[7]陶功权，李霞，温泽峰，等.两种轮轨接触应力算法对比分析[J].工程力学，2013，30（8）：229-235.

[8]邓永权，梁红琴，蔡慧，等.考虑车轮材料空洞的高速轮轨接触应力分析[J].机械科学与技术，2016，35（6）：933-938.

[9]赵鑫，金学松，温泽峰，等.全滑动状态下轮轨接触热弹性应力[J].西南交通大学学报，2008，43（1）：51-56.

[10]刘洋，蒋硕，吴亚平，等.剥离掉块对轮轨滑动接触热弹塑性的影响[J].交通运输工程学报，2016，16（2）：46-55.

[11]潘高峰，吴亚平，刘洋，等.钢轨错牙接头区轮轨接触的热弹塑性分析[J].兰州交通大学学报，2017，36（1）：105-111.

[12]CHEN Y C， LEE S Y. Elastic-plastic wheel-rail thermal contact on corrugated rails during wheel braking[J]. Journal of Tribology， 2009，131（1）：1-9.