卷烟包装箱回收系统归集中心选址优化模型

李家斌，何世伟，胡红春，靳国伟

1 北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京市海淀区上园村3号 100044；

2 河南工程学院，工商管理学院，郑州市新郑龙湖祥和路1号 451191；

3 中国烟草总公司职工进修学院，烟草流通研究室，河南省郑州市鑫苑路7号 450008

1 引言

烟草行业传统包装使用方式消耗了大量一次性的瓦楞纸箱，在消耗了大量资源和资金的同时，也造成了社会环境负担的加重[1]。为解决这个问题，2013年烟草行业提出要建立卷烟包装箱回收系统（国烟办〔2013〕249号文件）。系统主要包括卷烟厂、包装箱回收归集中心（一般由原三产企业组成，以下简称归集中心）、烟草商业地市级配送中心（以下简称配送中心）三个具体实施的环节。在这个系统中，归集中心主要负责包装箱在某省内的归集、拣选、整理、分类、暂存等工作。归集中心的合理选择和建设无疑是整个逆向物流网络的关键和核心[2]。目前烟草行业关于归集中心的选择与建设尚在起步阶段，因此结合烟草行业的实际，开展对包装箱回收过程归集中心的选址优化研究，无疑具有重要现实意义与理论价值。

包装箱回收过程的归集中心的选址应归于逆向物流设施选址范畴，现阶段关于逆向物流设施选址的研究有不少[3-13]，但现有研究多针对的是一般生产企业产成品及其废弃物的逆向物流网络的选址，较少考虑包装容器回收的选址[13]。对包装箱回收过程的归集中心的选址方面的研究,尚处于空白阶段。以关键字“卷烟包装箱回收”搜索时，共找到相关文献5篇，其中两篇定性的分析了烟草行业包装箱的回收现状并提出了改善建议，却未进行深层次的量化分析[14-15]。其他相关的定量化研究有3篇，第一篇是王俊杰等针对包装废弃物运输问题，构建了其优化模型[16]，但该文针对的是其他行业和运输模型，并未涉及选址问题。第二篇是丁涛等[17]针对烟草商业物流网络的规划问题建立了相应的优化模型，但该文解决的是卷烟正向物流的网络优化问题，未考虑逆向物流及其选址问题。第三篇是李家斌等[1]针对卷烟包装箱回收过程的运输问题建立了定量化的模型，该文有一定借鉴意义，但该文针对的是逆向物流运输调度的优化，同样未考虑选址问题。

烟草行业作为一个特殊行业，其包装箱回收的过程具有封闭性、独立性等特征。另外，卷烟包装箱的另外一个特征是易损坏，一般一个卷烟包装箱能回收3～4次就不能使用，这就必须考虑损坏率对模型的影响。基于以上考虑，本文将回收包装箱合格率，卷烟厂空包装箱需求、建立归集中心的固定成本以及归集中心的处理容量等因素引入模型，建立了总成本最小的包装箱回收系统的归集中心选址优化模型，为行业相关的战略性选址优化方面提供参考。

2 选址优化模型建立

2.1 卷烟包装箱回收运作流程及相关假设

卷烟包装箱的回收主要包括卷烟厂、归集中心、配送中心三个具体环节。其详细的运作流程如图1所示：

首先，每个配送中心上级的烟草销售公司依据卷烟的销售情况，向卷烟厂采购成品卷烟，随后卷烟厂将卷烟运输到各配送中心。其次，配送中心将成件卷烟打开并依据送货路线分拣打码卷烟。同时，收集空卷烟包装箱。待空包装箱收集到一定规模后配送中心通知卷烟厂回运，卷烟厂通知归集中心将各配送中心的空包装箱回运至归集中心。最后，归集中心依据卷烟厂的生产安排将包装箱送至卷烟厂。卷烟厂经过质量检查后，合格的包装箱进行重复利用。如果送来的旧包装箱量不能满足生产的需求，则卷烟厂可向包装箱生产企业采购新的包装箱。

图1 包装箱回收运作图Fig.1 The path of cigarette packaging boxes recycling

为方便构建模型，依据行业情况做下面假设 ：

a.因为行业卷烟历史销售数据较丰富，因此可做出较为准确的包装箱回收和需求预测，因此假定各配送中心的单位时间的卷烟包装量回收量和各卷烟厂的空包装箱需求量提前预知；

b.考虑到未来行业工业生产点的整合优化，发展尺寸统一、印刷简化的通用包装箱的趋势，本文只考虑一个规格的包装箱（或销量最大的包装箱）。

c.只在各配送中心处回收包装箱,且各环节间单位数目的空包装箱的运输费用确定；

d.各待建的包装箱回收归集中心的处理容量、固定建设成本确定。

e.配送中心、归集中心、卷烟厂等环节的包装箱回收合格率依据历史数据取平均值，其值已知。

f.当包装箱需求不能通过回收的旧包装箱满足时，卷烟厂可以以已知的价格采购新的包装箱。

2.2 模型建立

文中使用的主要参数和变量等见表1所示：

表1 主要参数和变量Tab.1 Parameters and Variables

模型的其他部分如下：

目标函数：

装箱由配送中心运往归集中心的运输费用和将其从归集中心回运至卷烟厂的运输费用；第二个费用是建设归集中心的固定成本； 第三个是卷烟厂因回收的旧包装箱不满足需求时采购的新包装箱的费用。式（2）～式（7）为约束条件。其中式（2）表示从配送中心发送给归集中心的包装箱数量约束。式（3）表示建立的归集中心的处理容量约束。式（4）表示归集中心的流量平衡约束，即从任意一个归集中心的合格包装箱全部都离开了该归集中心。式（5）表示卷烟厂的包装箱使用量等于回收的包装箱量加上新包装箱采购量。式（6）表示考虑到资金，人力，物力的约束，对建立的的归集中心个数有最大的限制。式（7）为回收包装箱量的取值非负约束和选址变量的0-1整数取值约束。

2.3 模型求解方法

通过对模型的分析可知，上述的模型为混合整数规划模型，可采用CPLEX，LINGO，GUROBI等优化软件进行求解。本文将以某省烟草行业的包装箱回收相关数据为案例，在建立的模型基础上利用CPLEX12.4软件进行模型的验证和讨论。

3 选址模型的应用与讨论

3.1 实验数据及所得结论

借鉴采用文献[1]中部分数据，考虑优化一个由18个配送中心（编号为配送中心 1-18）、7家卷烟厂（编号为卷烟厂1-7）和8家备选归集中心（编号为归集中心1-8）组成的包装箱回收网络，现要决策建设2个归集中心，应选择两个归集中心使总费用最小。

配送中心、归集中心、卷烟厂的相关数据见表2-6中所示，三个环节的回收包装箱合格率依据统计情况假设为0.8。其他数据来自于企业统计报表，其中表5，表6表示的单个包装箱的运输费用是依据行业统计数据结合两两环节之间的运输距离变换得到。

表2 各配送中心包装箱回收数目（千只）Tab.2 Quantity of packaging boxes in distribution centers returned (1000 piece.)

表3 卷烟厂包装箱需求量及单位采购成本Tab.3 Demand and unit price of packaging boxes in cigarette factory

表4 备选归集中心处理容量及建设固定成本Tab.4 The processing capacity of the recycling centers and the fixed cost for construction of the recycling centers

利用IBM ILOG CPLEX 12.4提供的OPL语言将以上的模型和数据编制程序，在 Intel（R）Core（TM）2 Duo CPU @ 2.13GHz，内存3G，Windows7操作系统下，程序运行时间少于5s，其求解的结果具体如下表7所示。

表5 配送中心与备选归集中心之间单位运输费用(元/千只)Tab.5 The transport rate between distribution center and recycling center (yuan/ 1000 piece.)

表6 备选归集中心与卷烟厂之间单位运输费用表(元/千只)Tab.6 The transport rate between factory and recycling center(yuan/ 1000 piece.)

表7 包装箱归集中心选址优化方案Tab.7 Optimal site selection scheme of recycling center

其中，求得目标值最小总费用为52949.6（千元），其中从配送中心回收到归集中心的旧包装箱总计有5700千只，从归集中心回收到卷烟厂的总计有4560千只，配送中心到归集中心的运输量和归集中心到的卷烟厂运输量分别如表8和表9所示。卷烟厂需采购5352千只新包装箱才能满足生产的包装需求。在备选位置1和位置2建设归集中心总的费用最低。

表8 配送中心到所选归集中心的运输量Tab.8 The dispatching quantity from distribution centers to recycling centers

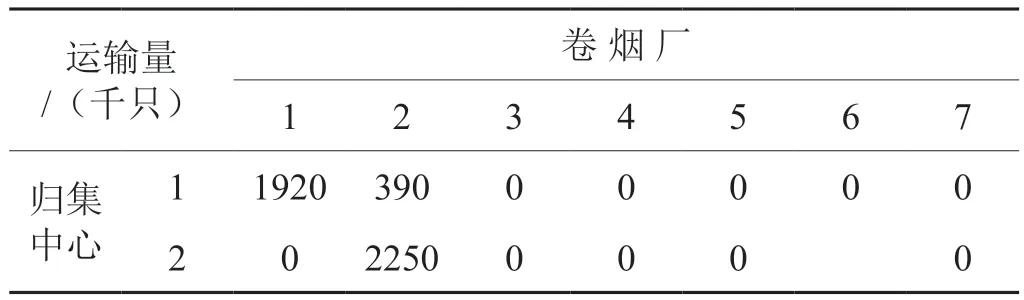
表9 所选归集中心到卷烟厂运输量Tab.9 The dispatching quantity from recycling centers to the cigarette factories

3.2 结果分析与讨论

在允许设置最大归集中心数目对总费用的影响方面。从表10可以看出，当允许设置最多1个归集中心时选择位置3，总费用57168千元，当允许最多设置2个归集中心时选择位置1，2，总费用52949.6千元；当允许最多设置3个以上归集中心时，最优决策是选址3个位置，并选择位置1，5，7，总费最低为52402千元；从中也可以看出，在归集中心的数目选择上，选择一个和两个成本差异较大，而选择3个归集中心为最优决策，总费用最低，当然该结论主要针对的是依据现有的数据情况得出的结论。

在包装箱采购成本的影响方面，若采购价格增加2元，则采购量从5352千只减少到5108.8千只，回收量则相应增加。若采购价格减少至4.5元，则总采购量增加至5736千只，而空包装箱回收量减少，当采购价格减少到2.5元每只时，总采购量增加到了9000千只，也即回收包装箱从经济角度来说已没有价值，具体如表11所示。

表10 仓库数目对采购量、总费用、选址位置等的影响Tab.10 The impact of the number of recycling centers on the purchasing quantity,the total cost and site selection of recycling centers

表11 采购价格对采购量、总费用、选址位置等的影响Tab.11 The impact of the price of cigarette packaging boxes on the purchasing quantity,the total cost and site selection of recycling centers ×1000 piece

4 结论与展望

本文建立了成本最小的包装箱回收过程中的归集中心选址决策模型。运用某省烟草行业包装箱回收数据对模型进行了验证。分析了归集中心的数目和采购价格对采购总量，回收量和选址方案的影响。作为初期研究，本文在对烟草行业包装箱回收系统的建模过程中对一些因素进行了简化，如只考虑一种包装箱，若需考虑多种包装箱，需求不确定因素等现实情况，这将在后期深入研究。