关于汽车结构设计中存在轻量化极限的分析*

2019-09-04刘雨婷胡代钧刘献栋单颖春路洪洲

汽车工程 2019年8期

刘雨婷，胡代钧，刘献栋，单颖春，路洪洲

（1.北京航空航天大学交通科学与工程学院，北京 100191； 2.中信金属有限公司微合金化技术中心，北京 100191）

前言

轻量化的主要途径包括以下3种：结构优化设计、轻量化材料的应用和先进制造工艺的应用［1］。轻量化材料目前以高强钢、铝和镁合金、复合材料等为主要选择［2］，在汽车零部件上，铝合金的使用从20世纪80年代的4%提升到了2010年的29%［3］。国外从20世纪80年代就有轻量化方面的研究［4］，数据表明1980-1995年期间北美中级轿车的质量平均每年降低了0.9%［5］。美国还推出新一代汽车共同开发计划致力于家庭用车的轻量化［6］。近年来许多汽车都采用全铝车身，例如奥迪公司ASLQuatrro的质量比同类车型减轻40%［7］。提高所使用钢板强度进而减薄板厚以达到轻量化目标，因原理简单且不需要大幅调整制造工艺，已成为汽车企业轻量化设计的首选［8］。本文中在针对一款轿运车进行结构轻量化设计时发现，对给定的结构，存在确定的材料强度上限和轻量化极限。但关于结构类型、面向轻量化的材料强度极限和密度极限等之间的关系的系统研究，目前尚鲜见文献报道。

针对这些问题，本文中通过理论分析和计算研究了3种截面的梁结构在固支-简支的支承、均布载荷加载的条件下，分别使用钢、铝合金和镁合金3种不同材料，在不同减重模式下的最大挠度和强度极限，得出了不同截面和材料的梁结构轻量化极限、经济强度及其影响因素。

1 问题引入

在针对如图1所示的某中置轴式轿运车进行轻量化设计过程中，将部分梁的截面厚度作为设计变量，同时保证足够的强度和刚度。由于企业引进了屈服强度更高的高强钢，希望能应用于此车架，以进一步降低车架质量。

图1 轿运车有限元模型图

调整优化方案时发现，无法在保证变形要求的情况下进一步减重。分析其原因是：高强度钢材的使用可提高强度裕度，仅从强度角度而言，可容许的结构厚度进一步减小；但是结构厚度的减小使结构刚度降低，其变形超过其极限值，因此仅通过选用更高强度的钢材，结构轻量化有明确的限值且存在材料强度上限。为便于叙述，给出材料经济强度的概念，定义如下：基于结构刚度限值，在最大减重率情况下，结构所需材料的最小屈服强度。

2 模型的建立与求解

2.1 模型的建立

商用车的车架主要由各种形式梁经过焊接、铆接或螺栓连接而成。为较真实地反映受力情况，以固支-简支梁为例进行结构轻量化设计过程中高强度材料的强度极限分析。

取梁的长度为1 m，选取常用的实心梁、空心梁和工字梁为例进行分析。假设实心梁的初始截面为10 mm×10 mm，取3种梁初始截面积相等，也即3种截面梁初始质量相等，如图2所示。

考虑到应力变化范围较大，为更好表征材料的强度极限，取常用的强度较低的Q235钢作为初始应力参考值，其屈服强度为235 MPa。本文中取其安全因数为1.8，即将131 MPa作为材料的许用应力，以确定施加于原结构的均布载荷。经计算，使实心梁产生的最大应力等于许用应力131 MPa所须施加的均布载荷为175 N／m。建立的模型如图3所示，并假设结构容许的最大挠度为15 mm。

图2 3种梁截面示意图（长度单位mm）

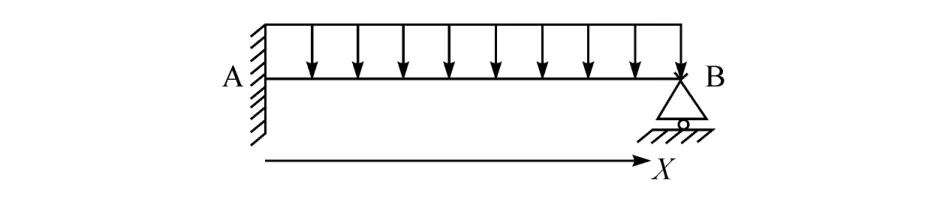
图3 梁模型示意图

定义轻量化率为

式中：W0为结构的原始质量；Wc为改变截面或材料后的质量。

2.2 模型求解

图3所示的梁模型是超静定结构。根据平衡方程，设梁上任一点处到A点距离为x，为计算该梁的挠度，将其分为只考虑均布载荷和只考虑简支处支反力作用两个部分进行计算，再叠加得出实际挠度，得出梁的总挠度为

式中：q为作用在单位长度上的力；E为弹性模量；I为截面极惯性矩；l为梁长度。

式（2）中，当 w′＝0时，x＝0.579 m，即可求得实心梁的最大挠度w＝5.4 mm。考虑商用车结构一般为塑性材料，根据Von Mises强度理论［9］进行强度计算，即

对梁模型而言，σmax＝M／Wz，其中 Wz为抗弯截面系数。

式中：b为截面宽度；h为截面高度。

可以求得，最大值σr3＝131 MPa。

假设3种截面的减重模式如图4所示。可归纳为两种，第1种为整体向内缩小，第2种为外轮廓不变，厚度减薄。其中，实心梁和工字梁采取第1种模式减重，空心梁属于第2种。

图4 3种截面梁减重模式

3 不同截面钢制固支-简支梁结构的强度和轻量化效果分析

3.1 实心截面梁结构强度和轻量化效果

计算实心梁各处应力值和挠度值，结果如图5所示。

图5 实心梁受力分析图

对于钢制实心梁，在均布载荷作用下，由式（2）和式（3）得，最大应力为131 MPa时，最大挠度为5.4 mm；取最大挠度的倒数作为结构刚度的表征值，而最大应力可表征结构所需材料强度。

假设设计时对结构要求是最大挠度不超过15 mm。根据图6可以得到，在此限制下能实现的最大轻量化率为39.94%，此时梁的最大应力为282 MPa，为保证安全应使用屈服强度不低于508 MPa的高强钢，即材料的经济强度为508 MPa。此工况下，若使用更高强度的材料，系统是安全的，但是强度裕量过大，导致成本提高、材料浪费。

图6 实心梁结构刚度、强度与轻量化率的关系

3.2 工字梁轻量化效果

如果改变截面形式，使用工字梁，由于截面惯性矩增大，将可在实心梁减重的基础上进一步减重。在上述载荷如边界条件下，相同质量的工字梁（所用截面尺寸如图2所示），原最大挠度均为1.7 mm，明显低于实心梁的最大挠度，当限制材料最大挠度仍为15 mm时，如图7所示，工字梁的最大应力为406 MPa，减重84.63%。因此对于该结构来说，轻量化率是84.63%，材料的经济强度为731 MPa。

图7 工字梁结构刚度、强度与轻量化率的关系

显然，使用工字梁具有更显著的轻量化效果，但材料的经济强度更高。

3.3 空心梁轻量化效果

如果进一步改变截面形式使用空心梁。由于与工字梁具有相同的抗弯截面系数和极惯性矩，改变其减重模式可进一步减重。在相同的载荷和边界条件下，与实心梁、工字梁初始质量均相同的空心梁（截面尺寸见图2），原最大挠度为1.7 mm，明显低于实心梁的最大挠度，当限制材料最大挠度为15 mm时，如图 8所示，空心梁的最大应力为530 MPa，轻量化率可达91.28%。因此改变梁的减重模式，提高了通过改变结构厚度达到轻量化的潜力，这样在满足刚度要求的前提下允许采用更高强度的材料实现更大程度的轻量化，此时所用材料的经济强度为954 MPa。