基于智能体理论的横向互联空气悬架控制研究*

2019-09-04李仲兴管晓星

汽车工程 2019年8期

李仲兴，管晓星，江洪

（1.江苏大学汽车与交通工程学院，镇江 212013； 2.江苏大学机械工程学院，镇江 212013）

前言

空气悬架以空气弹簧作为弹性元件，因其优良的性能在车辆领域得到了广泛的运用。互联空气悬架作为空气悬架的衍生结构，由Higginbotham于1961年提出［1］。Friendrich等建立了互联空气悬架数学模型并通过台架试验验证其准确性［2］；Dvais通过试验得出重型货车通过增大纵向互联管路内径能够有效减小车轴对底盘施加的动载荷，并提出悬架力相关度系数分析和T-test试验两种关于悬架动载荷分配的分析与评价体系，进一步论证了纵向互联结构的均载作用［3-4］；崔振建立横向互联空气悬架整车模型并搭建整车台架研究系统静动态特性［5］；钱宽对不同互联形式下悬架的振动特性和整车性能进行了仿真与试验研究［6］；琚龙玉提出了仿天棚互联状态控制策略，研究表明该策略在提升悬架隔振和消扭能力的同时保证了车辆的操纵稳定性［7］。

在现代控制系统中，人们对逻辑问题和决策问题越来越重视，因此对具有自治性和学习性的智能体技术的研究日益增多。慎思型智能体的代表BDI（belief-desire-intention）是一种较为成熟的模型，学术界普遍认为该模型是一种方便灵活、能够有效适应复杂动态环境的智能体结构［8］。Bratman在对理性与意图两者之间的关系进行哲学分析后提出了BDI模型［9］。Rao和 Georgeff提出了一个形式化理论和抽象BDI解释器，将BDI模型引入软件智能体［10］。传统的BDI模型存在一定的局限性，例如不存在内部的学习结构、不能处理不确定性下的决策等。因此，国内外学者结合研究需求，适当增加或者修改相应的概念，得到合适的BDI模型用于自身研究。Farias建立了模糊感知的BDI模型解决信息不完全环境下的决策问题［11］。Dominguez等利用BDI智能体系统解决无人机在空中移动的人机协作问题［12］。刘岳鹏基于BDI模型对空中仿真系统的管制员进行建模，提出并设计了管制员学习行为［13］。

从目前的研究情况来看，学者们对互联空气悬架的研究多集中在特性研究方面，对互联空气悬架的控制研究较少。为更加充分发挥横向互联空气悬架的优势，将智能体技术引入其互联控制研究中。本文中首先建立横向互联空气悬架整车模型并通过试验验证其准确性。在此基础上构建横向互联空气悬架互联状态控制智能体系统，其中具有自学习能力的仿天棚互联状态控制智能体是该系统的关键组成部分，它以仿天棚互联状态控制策略中关键参数滞回区间为控制对象，输出适合于当前环境状态的最优滞回区间，能够提高仿天棚互联状态控制策略对行车过程中动态环境的适应能力，充分发挥该策略的控制效果，使车辆在行驶过程中获得良好的整车综合性能。

1 横向互联空气悬架整车7自由度模型及试验验证

1.1 整车动力学模型

根据研究需求，对四轮车辆物理结构进行适当简化，建立包括车身垂向、侧倾、俯仰运动和4个车轮垂向振动的整车7自由度模型，简化后的横向互联空气悬架整车振动模型如图1所示。

图1 横向互联空气悬架整车模型

图中：Mb为车身质量；Zcg为簧上质量质心的垂向位移；Mt为轮胎质量；Zti（i＝1，2，3，4）为 4个簧下质量质心的垂向位移；lf，lr分别为前、后轴到质心的距离；Kt为轮胎刚度；qi（i＝1，2，3，4）为路面施加于 4个簧下质量的垂向激励；Ir为车身绕侧倾轴线（X轴）的转动惯量；θ为车身侧倾角，以车身右倾为正；Ip为车身绕俯仰轴线（Y轴）的转动惯量；φ为车身俯仰角，以车身前倾为正；Bf为前轴轮距；Br为后轴轮距。

其动力学方程为

其中

式中：Fi（i＝1，2，3，4分别对应前左、前右、后左、后右4个悬架位置）为4个悬架空气弹簧与减振器的合力；pa为大气压力；Aei（i＝1，2，3，4）为 4个空气弹簧有效承载面积；c为减振器阻尼；fdi（i＝1，2，3，4）为4个悬架动行程。

1.2 横向互联空气弹簧模型

将空气弹簧视为开口绝热系统，其气体运动方程为

式中：const为常数；pi（i＝1，2，3，4）为 4个空气弹簧内气体压力；Vi（i＝1，2，3，4）为 4个空气弹簧气室容积；mi（i＝1，2，3，4）为 4个空气弹簧中的气体质量；κ为绝热指数，对于空气，其值为1.4。

考虑互联管路的节流效应，将互联管路的节流效应等效为节流孔，其质量流量可表示为

式中：pup为上游气体压力；pdn为下游气体压力；Tup为上游气体温度；At为有效通流面积。

考虑互联管路沿程损失与时滞效应，互联管路不同位置处气体质量流量随时间变化的函数可表示为

式中：L为管路长度；pdn为管路末端气压；Tdn为管路末端温度；c为声速；Rt为连接管路内壁阻力系数；R为气体常数，对于空气，R＝287 N·m／（kg·K）。

1.3 仿真分析

在MATLAB／Simulink环境下建立7自由度横向互联空气悬架整车仿真模型，对车辆前左车轮施加阶跃激励，加速度响应如图2所示。对车辆施加侧向加速度，车身侧倾角变化如图3所示。

从图2可以看出，横向互联空气悬架能够更快衰减簧上质量加速度，提高行驶平顺性。从图3可以看出，转弯时空气悬架互联会降低车辆的操纵稳定性。因此进行互联控制研究有其必要性。

1.4 模型验证

图2 前左簧上质量加速度响应

图3 车身侧倾角随侧向加速度的变化

为验证所建立的模型的准确性，基于MTS-320 4通道液压伺服激振试验台，搭建横向互联空气悬架整车试验台架，如图4所示。对车辆前左轮施加振幅为15 mm的正弦扫频激励，激振频率为0.75～7.25 Hz，每秒提升0.025 Hz，并将试验结果与仿真结果进行对比，如图5所示。

图4 横向互联空气悬架整车试验平台

对四轮施加激励，模拟车辆以70 km／h的车速行驶于路面不平度系数为256×10-6m3的道路，试验时间为300 s，并将试验结果与仿真结果进行对比，如表1和表2所示。

由图5和表1、表2可知，仿真结果与试验结果吻合度较高，证明所建立模型准确可靠，可在此模型的基础上进行互联状态控制智能体系统的研究。

图5 前左簧上质量加速度均方根值随激励频率的变化

表1 非互联状态下簧上质量加速度均方根值

表2 互联状态下簧上质量加速度均方根值

2 基于BDI模型的仿天棚互联状态控制智能体系统构建

2.1 仿天棚互联状态控制策略原理及实现

横向互联空气悬架是在传统空气悬架的基础上，利用互联管路将同轴左右两个空气弹簧连通，实现左右空气弹簧中气体自由交换的一种悬架形式。横向互联空气悬架能提升车辆隔振、消扭能力，改善轮胎接地性，提升行驶平顺性，但是在高速转向时会加剧车身的侧倾，因此需要制定合理的互联状态控制策略，通过互联管路中电磁阀对互联状态进行控制，保证车辆的综合性能。

文献［7］中提出了仿天棚互联状态控制策略，该策略原理为：当簧上质量侧倾方向与其受到的总弹性回复力偶矩方向一致时互联状态开启，从而减小簧上质量侧倾运动的推力矩；当簧上质量侧倾方向与其受到的总弹性回复力偶矩方向相反时互联状态关闭，从而增大簧上质量侧倾运动的阻力矩。该策略监测参数为簧上质量侧倾角θ和簧下质量侧倾角θt，其中θt的定义为同轴左右簧下质量质心连线与水平面所呈夹角，如图6所示。

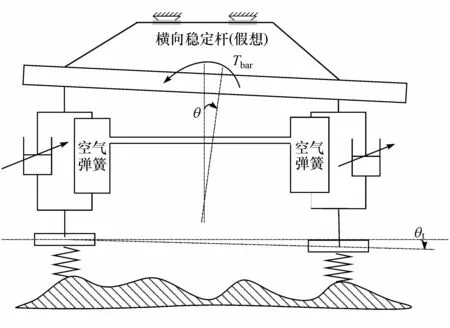
图6 仿天棚互联状态控制原理示意图

应用于互联状态仅有“开”、“闭”两种选择的横向互联空气悬架时，仿天棚互联状态控制规则退化为

式中：kroll＝krollmax，代表互联状态“关闭”；kroll＝krollmin，代表互联状态“开启”。

在仿真模型中，互联状态的开闭是通过改变互联管路的有效面积At来实现的。式（6）仿天棚控制规则在模型中变形为

式中：At-1为上一时刻的互联管路有效通流面积；δmin为滞回区间下边界；δmax为滞回区间上边界。

滞回区间对车辆行驶时的综合性能有着显著的影响，针对不同的行驶工况设置不同滞回区间，能够充分发挥仿天棚互联状态控制策略的优势。

2.2 横向互联空气悬架互联状态控制智能体系统结构

基于智能体理论建立仿天棚互联状态控制智能体系统，包括仿天棚互联状态控制智能体、传感器信息采集模块和互联状态控制模块，如图7所示。

图7 互联状态控制智能体系统

信念表示智能体对于环境的认知。仿天棚互联状态智能体感知环境状态信息，经过信念产生器生成行驶平顺性评价指标和操纵稳定性评价指标，以这两项评价指标作为自身信念并存入信念库中。

愿望表示智能体希望自身达到或者保持的状态。仿天棚互联状态控制智能体根据行驶平顺性指标和操纵稳定性指标建立综合评价指标，其愿望即为使车辆在行驶中达到更好的综合性能。

强化学习是智能体从环境状态到行为映射的学习，以使数值回报达到最大［14］。采用强化学习机制的智能体自身带有确定的动作集，感知环境状态，根据动作选择机制执行一个动作并做出评价，如图8所示。经过大量训练，最终能得到一套状态—动作映射关系。仿天棚互联状态控制智能体的学习问题可最终归结为“探索利用”（exploration-exploitation）问题。一方面，仿天棚互联状态控制智能体根据强化学习算法在动作集中选择目前为止回报最高的动作，称之为利用；另一方面，这个目前为止回报最高的动作不一定是最优动作，还需选择可能回报更高的动作，称之为探索。其关键是保持探索和利用的平衡，在有限的选择中使得仿天棚互联状态控制智能体的收益最大化。

意图表示智能体在愿望中选取的当前最需要或最适合完成的一个，即智能体下一时刻执行的动作。对于仿天棚互联状态智能体而言，其意图由学习模块和愿望模块共同决定。

2.3 横向互联空气悬架互联状态控制智能体系统的实现

图8 强化学习

在实际建模过程中，仿天棚互联状态控制智能体从传感器信息采集模块中感知环境状态信息至信念产生器，包括 4个簧下质量加速度 ati（i＝1，2，3，4）、车速 v、车身侧倾角 θ、车身侧向加速度 ays、车身前左簧上质量3个方向加速度ax，ay，az。智能体通过车速v、路面不平度Gq（n0）和车身侧向加速度ays对车辆所处环境进行辨识，其中路面不平度Gq（n0）可以由簧下质量加速度信息和车速信息处理后获得［15］。由于以上为连续变量，需将其进行离散化，综合考虑计算量与划分精度等，v离散化为F（F＝9）种状态，ays离散化为 G（G＝4）种状态，Gq（n0）离散化为H（H＝8）种状态，由此建立行驶平顺性信念矩阵RCbel、操纵稳定性信念矩阵HSbel和综合评价指标矩阵Zdes。

参考 GB／T4971—2009《汽车平顺性试验方法》，选取车身前左簧上质量x，y，z 3个方向的总加权加速度均方根值aw作为行驶平顺性评价指标：

式中 axw，ayw，azw分别为 x，y，z方向加权加速度均方根值。

考虑实际行车过程中的可实施性，选取侧倾因子R作为操纵稳定性评价指标［16］：

式中：m为总质量；mb为簧上质量；B为轮距；hR为侧倾中心的高度；hs为车身质心到侧倾中心的距离；ays为车身侧向加速度；θ为车身侧倾角。

信念产生器感知环境状态信息生成新的行驶平顺性信念aw_new和新的操纵稳定性信念Rnew，并进行信念修正：

式中：aw_i为修正后的行驶平顺性信念；aw_i-1为RCbel矩阵中相应环境状态下的行驶平顺性信念；Ri为修正后的操纵稳定性信念；Ri-1为HSbel矩阵中相应环境状态下的操纵稳定性信念；p为信念修正的权重系数，p∈［0，1］。

智能体将修正后的信念储存至信念库RCbel矩阵和HSbel矩阵对应坐标下，该坐标由当前车速、侧向加速度和路面不平度所处状态f，g和h决定。

愿望产生器利用信念库中的信念进行推理行为，将信念矩阵中同一环境状态坐标下的行驶平顺性信念和操纵稳定性信念进行归一化，消除行驶平顺性信念和操纵稳定性信念之间的量纲影响，随后建立综合评价指标并存入Zdes矩阵中作为强化学习的回报：

式中：J为综合评价指标；JRC为归一化后的行驶平顺性信念；JHS为归一化后的操纵稳定性信念；ω为权重系数，ω∈［0，1］。

汤普森抽样算法是Thompson于1933年提出的基于贝叶斯主义后验可信区间的随机算法，又称随机概率配对算法［17-18］。与UCB算法、MOSS算法相比，汤普森抽样算法具有更好的经验效果，模拟试验中其后悔最低［19］。仿天棚互联状态控制智能体需要在实际行车过程中进行在线学习，因此选择学习过程稳健的汤普森抽样算法作为其强化学习算法。

经典汤普森采样算法中假设回报为均匀分布，但在实际问题中，回报的分布不尽相同，若直接采用服从均匀分布的回报则具有一定的局限性。利用仿天棚互联状态控制智能体仿真模型，观察在不同环境状态下智能体信念库中行驶平顺性评价指标aw和操纵稳定性评价指标R所服从的概率分布，部分仿真结果如图9～图11所示。图9为C级路面直线行驶时评价指标分布随速度变化曲线，图10为50 km／h直线行驶时评价指标分布随路面等级变化曲线，图11为B级路面50 km／h行驶时评价指标分布随侧向加速度变化曲线。

图9 评价指标分布随速度变化

图10 评价指标分布随路面等级变化

图11 评价指标分布随侧向加速度变化

由图9～图11可知，随着车速、路面和侧向加速度的变化，评价指标基本服从高斯分布，因此仿天棚互联状态控制智能体最终采用高斯-汤普森抽样算法。

采用高斯汤普森抽样算法的仿天棚互联状态控制智能体抽样过程如图12所示。该算法利用智能体感知的离散化环境状态信息，将当前车速、路面、侧向加速度坐标下全部滞回区间进行抽样，选择其中回报最高的滞回区间输出至意图库作为本次执行的动作。最后由意图库输出至互联状态控制模块，改变互联状态控制模块中的仿天棚互联状态控制策略的滞回区间。

图12 仿天棚互联状态控制智能体抽样过程

3 仿天棚互联状态控制智能体系统控制效果分析

3.1 单一行驶工况下系统控制效果

设计单一行驶工况如表3所示。考虑到计算量与计算精度，仿真时间设为 100 s，仿真步长为0.001 s。

表3 行驶工况

为保证仿真曲线清晰，图13～图20展示前20 s变化情况。其中，“平顺性改善率”的计算方法为“（非互联状态下的aw值-智能体控制下的aw值）／（非互联状态下的aw值-互联状态下的 aw值）”；“操稳性改善率”的计算方法为“（互联状态下的R值-智能体控制下的R值）／（互联状态下的R值-非互联状态下的R值）”。

图13 行驶工况1下评价指标的变化

图14 行驶工况2下评价指标的变化

图15 行驶工况3下评价指标的变化

图16 行驶工况4下评价指标的变化

从图中可以看出，互联状态控制智能体系统在不同行驶工况的表现有所不同。当车辆为直线行驶时，智能体控制下车辆行驶平顺性优于非互联状态下，在行驶工况1和行驶工况6时，行驶平顺性甚至接近互联状态，且操纵稳定性绝大多数工况下接近甚至优于非互联状态。当车辆为转向行驶时，智能体系统控制下车辆牺牲部分行驶平顺性来获得更好的操纵稳定性，且随着侧向加速度的增大，行驶平顺性的牺牲也相应增加，车辆性能接近非互联悬架车辆，提高车辆行驶安全性。

图17 行驶工况5下评价指标的变化

图18 行驶工况6下评价指标的变化

图19 行驶工况7下评价指标的变化

3.2 混合行驶工况下系统控制效果

图20 行驶工况8下评价指标的变化

为进一步验证横向互联空气悬架互联状态控制智能体系统的控制效果，在混合行驶工况下进行仿真，对比智能体系统控制下与互联状态、非互联状态下车辆的性能指标，图21所示为混合工况。

图21 混合工况示意图

根据表4和表5可知，在混合工况下，与传统的非互联空气悬架相比，智能体控制下的横向互联空气悬架的平顺性改善了54.9%；与互联空气悬架相比，智能体控制下的横向互联空气悬架的操稳性改善了85.2%。结果表明：仿天棚互联状态控制智能体系统能够权衡车辆的行驶平顺性和操纵稳定性，在保证行驶平顺性的同时，获得良好的操纵稳定性。