矿 物 颗 粒 度 对 粉 末 颜 色 的 影 响
2019-09-03王心华许家奇
王心华, 钟 芬, 徐 跃, 许家奇
(兰州大学 a. 物理学国家级实验教学示范中心; b. 物理科学与技术学院, 兰州 730000)
0 引 言
材料在研磨前后其颜色的变化受多种因素的影响,除了与其所用原材料的化学组分、材料类型、吸氧量、研磨温度等一些因素有关外,研磨前后的粒径分布也是其中的一个重要方面。在社会生活中,材料、能源、医药、冶金、化工、电子、机械、建筑及环保等诸多领域都与材料的粒度分布有关[1-5]。从矿物颜料颗粒度对色貌的影响这一角度出发, 基于光学角度,分析随着颜料颗粒度的变化而导致的色彩属性的变化,也可为文化遗产真实的数字化典藏、艺术品的高保真复制以及历史文物色彩的真实虚拟再现提供理论支持。微米级别的矿物颗粒的许多性质与块状材料不同,研究其自然状态下的性质具有一定的实际意义[6-10]。即使是相同的材料,微米颗粒与块状的在很多方面的特性也有一定的差异,因此,采用一般的针对块状材料的颜色测定方法来测定微米矿物颗粒显然是不适用的。本文通过紫外-可见光谱仪测量粉末在一定范围内的漫反射系数,并采用Mie散射理论,从光学角度研究同种颜料不同颗粒度下的明度、色调以及饱和度的变化,以为它不同的应用提供理论基础。
1 基本理论
1.1 Mie理论[11]
Mie理论通过求解具有适当边界条件的Maxwell 方程组,得到均匀球形粒子的光散射描述。在一定条件下,也可以求解非球形粒子(主要为圆柱形、椭球形的颗粒)以及颗粒内部折射率不均匀粒子的光散射。Mie理论通常研究的粒径参数(x=2πr/λ)的范围为1左右。
1.2 CIE色度图[12]
国际照明委员会(Commission Internationale de L'Eclairage,CIE)制订了一系列色度学标准,一直沿用到数字视频时代,其中包括白光标准(D65)和阴极射线管(CRT)内表面红、绿、蓝3种磷光理论上的理想颜色。
2 实 验
(1) 实验原料。硅酸锆ZrSiO4,氧化铁Fe2O3,碱式碳酸铜Cu2(OH)2CO3,四氧化三铁Fe3O4。
(2) 实验设备。真空泵,行星式球磨机,X-射线衍射仪,Lambda950紫外-可见光谱仪,粒度分析仪。
(3) 实验方法。本实验采用球磨法制备不同粒径的样品[13-15]。每次称取相应的粉末样品12 g,装罐,首先进行3 min的抽真空处理,随后进行不同时间的球磨,最后取研磨不同时间后的样品进行XRD测试以分析球磨前后材料物相的变化情况,测200~700 nm范围内样品的漫反射光谱并计算在可见光范围内相对明度、色调及饱和度,以分析样品在研磨前后颜色的变化情况。所得样品分别为未研磨,研磨2、4、6 h。
3 结果与讨论
3.1 XRD结果分析
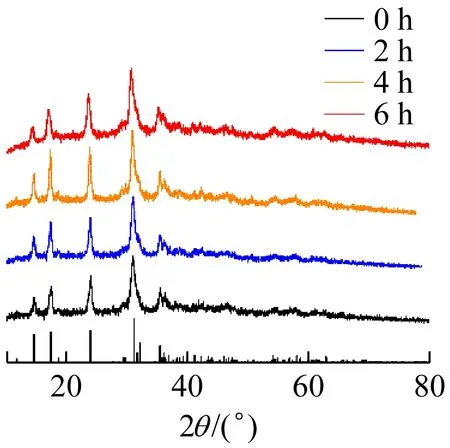
图1为ZrSiO4、Fe2O3、Cu2(OH)2CO3、Fe3O4的不同研磨时间所对应的XRD图。由图1(a)可以看出,未研磨的硅酸锆样品与研磨2、4、6 h样品的峰的位置相对应,强度也相同,且与国际标准卡片中该样品的峰的位置与强度也相匹配。因此可以确定硅酸锆样品在研磨前后的物相并没有发生改变,图1(b)~(d)也呈现出相同的变化规律。因此可以得出结论,各材料在研磨前后的物相均未发生改变,可以排除由于物相的改变导致其颜色变化这一影响因素。
3.2 反射光谱曲线与粒径分析
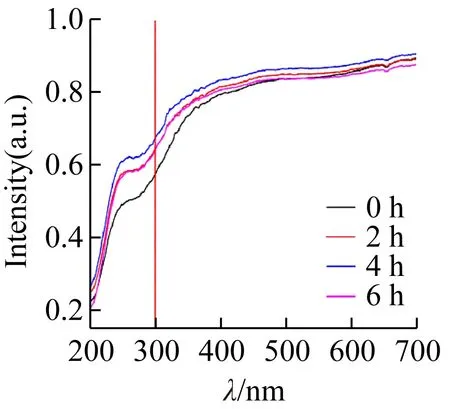
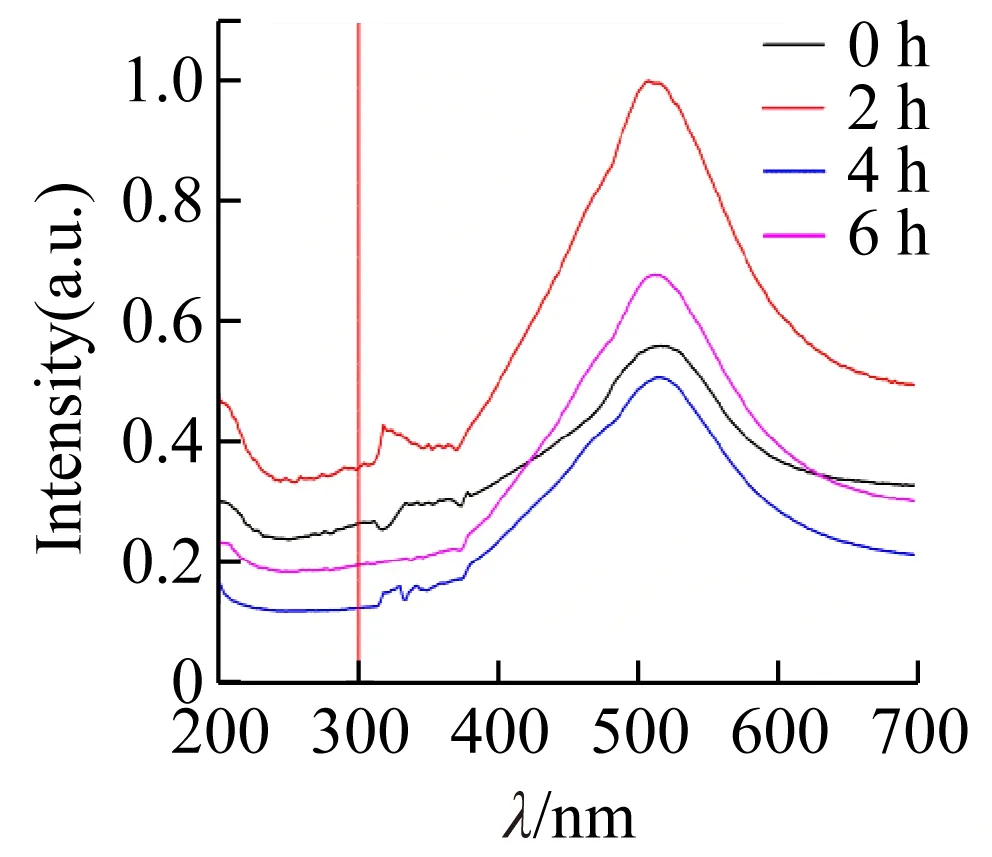
图2为ZrSiO4、Fe2O3、Cu2(OH)2CO3、Fe3O4的不同研磨时间所对应的200~700 nm范围内的漫反射光谱图。
(c) Cu2CO3(OH)2
(a) ZrSiO4
(c) Cu2(OH)2CO3
本文引入视见函数这一概念[16]:人眼对红、绿、蓝响应的视锥细胞数量比约为32∶16∶1,所以,人眼对不同波长的单色光产生相同的视觉效应,要有不同的辐射功率;在引起相同的视觉响应条件下,若光波长为λ的光所需要的光辐射功率为P(λ),而对光波长为555 nm的光(人眼对此波长的光最敏感)所需要的光辐射功率为P(555),则定义v(λ)=P(555) /P(λ)为波长λ的视见函数(见图3)。
取400~700 nm的可见光范围内的漫反射光谱曲线乘以视觉函数所对应明视觉相应范围内的值,得到各样品的相对明度值,如表1所示。
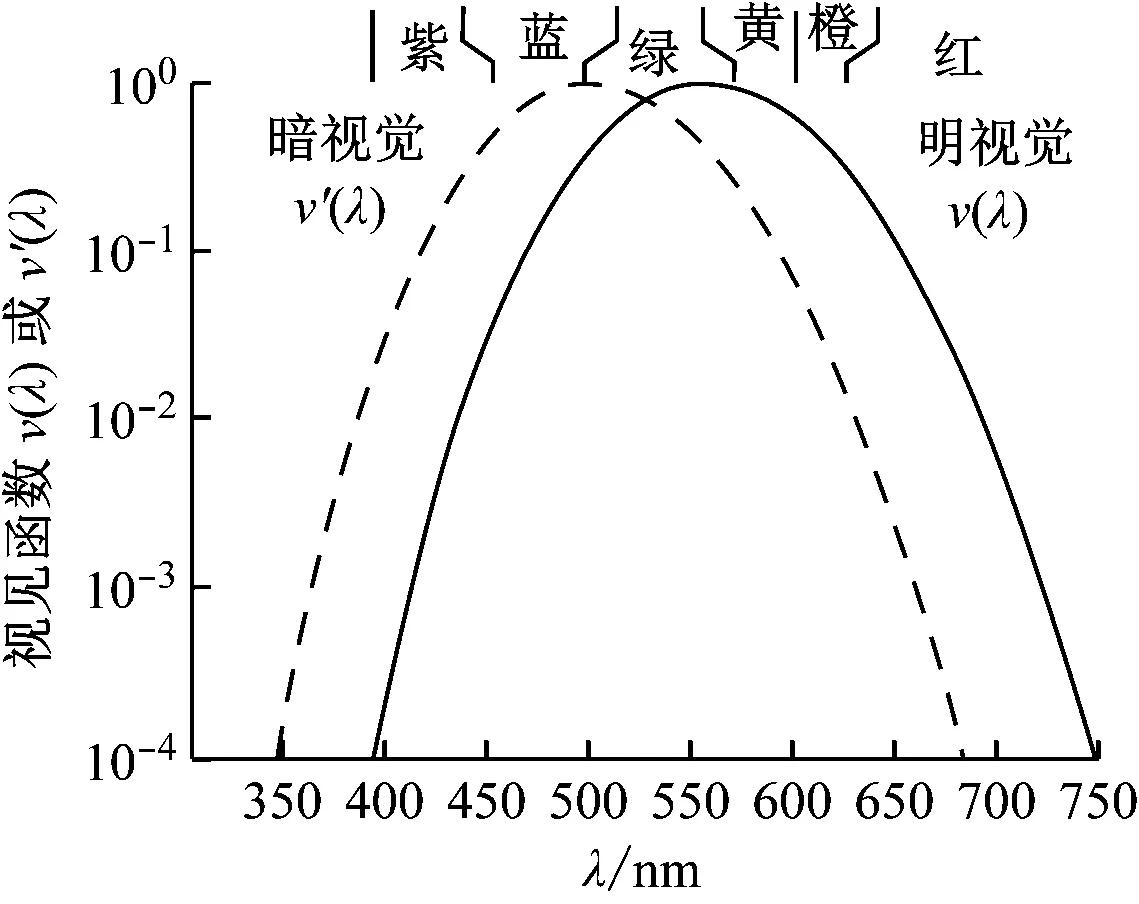
图3 视见函数
同时,选取其中一组样本 (Fe2O3) 通过粒度分析仪测量颗粒的平均直径,得到如下结果:0 h(2 509 nm)、2 h(3 531 nm)、4 h(4 456 nm)、6 h(2 459 nm);其中颗粒的平均直径呈现上下波动是由于团聚现象的产生。粒径在0.1~10 μm的粉末称为微粉体,粉体颗粒间存在凝聚力(附着力),包括范德华力、静电吸引力等,当颗粒尺寸变小时,颗粒的比表面积增大,表面能增加,使其成为不稳定的热力学体系,在凝聚力的作用下,颗粒自发团聚,以降低体系的吉布斯自由能[16]。通过对氧化铁样品计算出的相对明度值与粒径进行比较得出:粒径越大,明度也就越高,颜色也就越亮;粒径越小,明度也就越低,颜色也就越暗。同时由漫反射光谱数据得到的红色Fe2O3粉末的CIE色度图如图4所示。由图4可见,研磨前后的Fe2O3粉末的色调和饱和度均未发生改变,其他粉末的色度图也呈现出同样的结果。

(a) 0 h (b) 2 h (c) 4 h (d) 6 h
4 理论分析
4.1 定性理论分析
假设粉末颗粒呈球形,粉末平均直径为d,入射光波长为λ,记无量纲粒径参量
α≡πd/λ
(1)
对于红色Fe2O3粉末最小粒径可算得α≈13,适用于Mie散射模型[17]:当α≤1时,Mie散射可近似为瑞利散射;α≥1,Mie散射可近似为夫琅禾费衍射;α→∞,Mie散射可近似为几何光学理论。当入射光是自然光且光强I0时,散射光强为
(2)
式中:r是从球心到该点的距离;i1(θ)、i2(θ)是无量纲的散射光强度函数,与θ、α有关。由上述理论可知:
由计算机模拟可知[18],当其他变量一定时,α越大,球形颗粒的散射光强越强。对于颗粒群的多体散射,不同颗粒的散射光强非相干叠加,得到的总散射光强也应与α呈正相关。
4.2 计算机模拟
利用MiePlot软件选取模拟参数如下:入射光波长λ=589 nm,入射光强I0=1 W/m2,Fe2O3对于589 nm光的折射率n=3.01,环境折射率n0=1,散射角度θ=180°,观测点距球心距离r=1 m,颗粒直径变化范围d=2.4~4.5 μm(步长0.002)。
颗粒群数量和形态分布:球形颗粒50个,满足对数正态分布[19],直径标准差为粒径的20%。得到结果如图5所示。由图可见,散射光强大致与平均粒径呈正相关,只是有所波动罢了。

图5 计算机模拟结果
但实际情况,入射光通常为自然光,所以做了自然光条件下的模拟。在模拟参数中,入射光选太阳光谱,直径取4个值,都为粒度分析仪测得的粒径平均值,其他参数保持不变模拟图如图6所示。
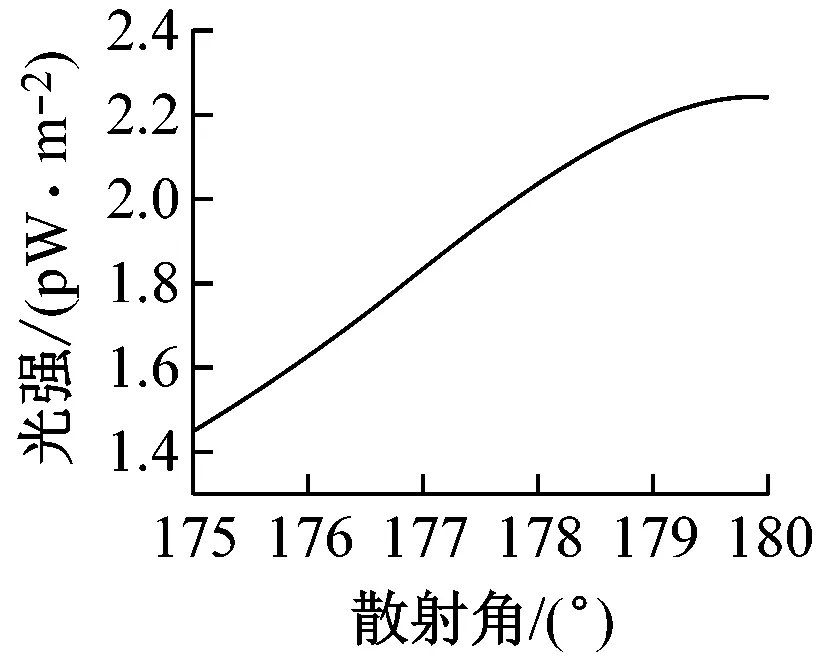
(a)d=2.459 μm
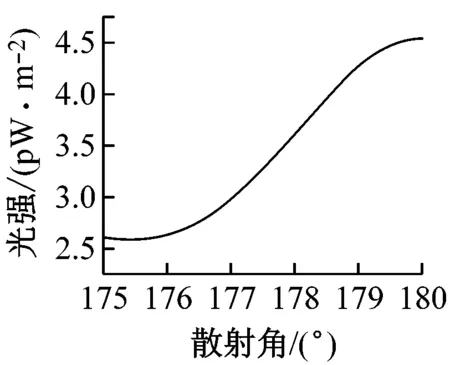
(b)d=3.509 μm
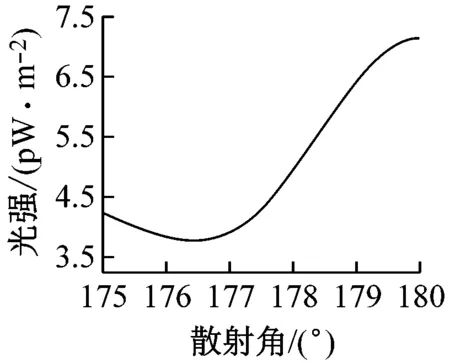
(c)d=3.531 μm

(d)d=4.456 μm
图6 模拟图
图7为模拟的180°散射光强与之前实验算得的相对明度相比较。可以看出,两者变化趋势一致,随着粒径增大,相对光强和明度都增大;这说明计算机模拟结果和我们的实验、理论分析相符。
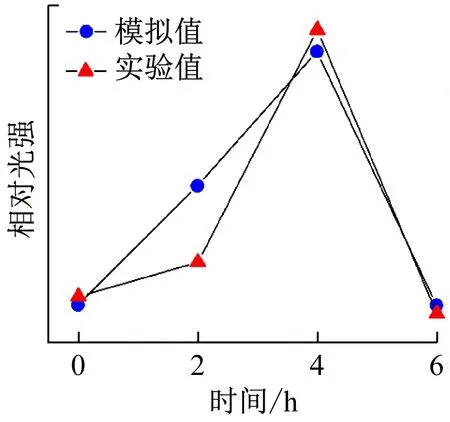
图7 180°散射光强模拟与实验对比
实际情况下,粉末颗粒为非球形,可利用椭圆截面处理任意形体颗粒群的重散射问题。通常情况下,非球形颗粒偏离球形程度越大,散射光的角分布越平坦,明暗分布也就越不明显;但是对总散射光强的影响较小[20]。在紫外可见漫反射光谱测量中其散射光强只与颗粒直径的呈正相关。由此可知,粉末粒径越大,漫反射进入人眼的光强越大,人感受到的颜色的明度越高。
对于等光强单色光入射,Mie散射不会改变其光的频率,只是不同波长光的散射强度可能会不同。我们知道,云呈现白色是因为Mie散射,散射光色调与饱和度基本与入射自然光相同。因此可以认为,Mie散射基本不会改变粉末的色调和饱和度。为证实此推测,又做了计算机模拟:图8、9是小粒径d=2.509 μm和大粒径d=4.456 μm的结果图;入射光强一定时,对于不同波长,其散射光强呈周期性波动,但由于颗粒形状不规则,波动范围会变小;同时,波动范围相比于物质对光的选择性吸收强度,可以忽略不计。
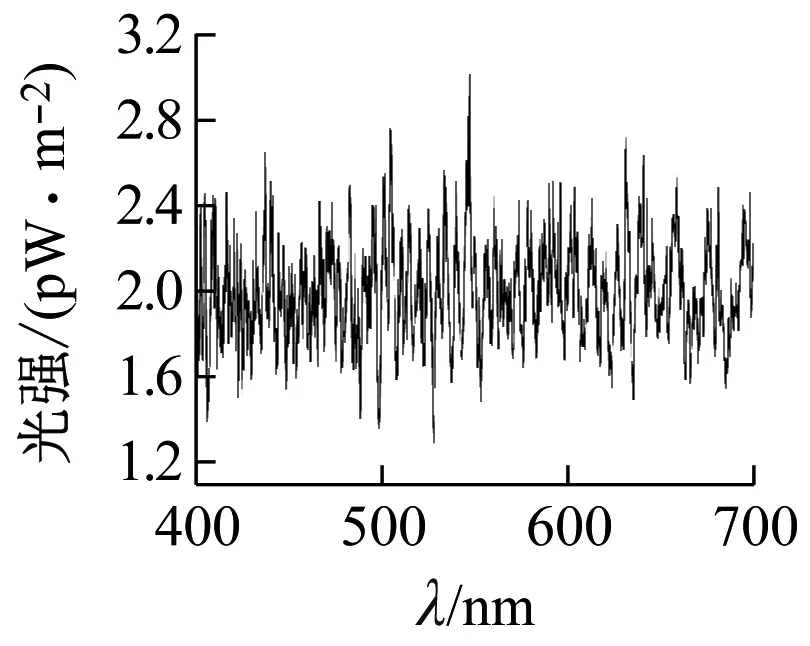
图8 小粒径模拟结果
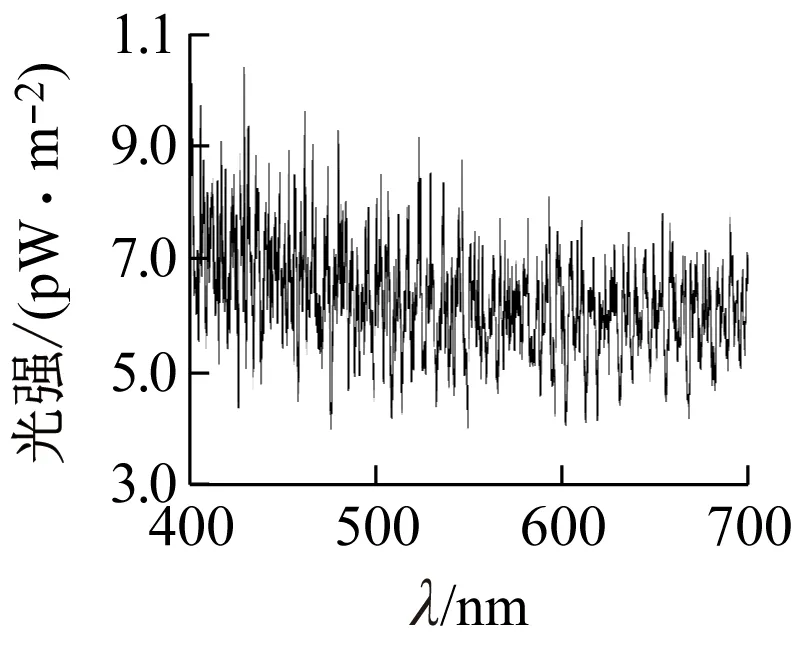
图9 大粒径模拟结果
5 结 语
本文制备并研究了级别的非金属粉末,通过研究,得出以下结论:研磨程度确实会影响粉末的颜色,研磨通过改变粉末的颗粒直径或物相来改变粉末的颜色。 粉末颜色的改变与颗粒的直径直接相关:粒径越大,明度越高,颜色越亮;粒径越小,明度越低,颜色越暗。粒径对色调、饱和度的影响很小。
