机翼结构试验杠杆系统位移计算和参数化建模

2019-09-03赵诗鸿于哲峰

实验室研究与探索 2019年8期

赵诗鸿，于哲峰

(上海交通大学航空航天学院，上海 200240)

0 引言

机翼作为飞机重要的承载部件，其承载能力决定了飞机结构的性能指标。机翼静强度试验根据不同载荷工况验证了飞机是否满足强度设计要求[1-2]。试验中通常采用作动器以及杠杆系统进行加载，首先将飞机飞行过程中可能受到的载荷(气动载荷、惯性载荷、集中载荷)简化为有限数量的集中载荷，并在试验件相应位置布置加载点；再通过多级杠杆系统将若干个加载点连接到同一个电液伺服作动器；根据各个加载点的载荷关系设计杠杆参数，在一个翼面上使用多个杠杆系统，即可模拟真实飞行情况下机翼的受载情况[3]。

近年来,陈江宁等[4]研究了加载系统与交互技术和加载系统配重优化设计方法。王正平等[5]探讨了飞机结构静力试验设计中的分布式载荷和集中式载荷的演算问题。刘金玉等[6]针对初教六机翼结构强度试验，使用VB语言在Visual Studio平台下计算了杠杆系统的载荷配重问题。侯峰[7]基于Microsoft Visual C++6.0开发了飞机结构试验设计软件的安装图设计模块，使用该软件可通过图形化人机接口进行加载系统中结构和设备安装关系的设计。巴塔西等[8]研究了基于CATIA二次开发的飞机结构试验加载杠杆系统参数化建模方法，利用Microsoft Visual Basic(MS-VB)实现了杠杆参数化建模以及杠杆加载系统的自动装配，可以快速地实现加载杠杆系统几何模型参数化生成。目前研究主要集中于结构试验前杠杆系统的设计和建模，对于在试验过程中杠杆位移的模拟并没有涉及到，而大型航空结构在试验中将产生显著的变形，如波音787客机在极限载荷试验中翼稍的位移超过7m.在该变形情况下，极有可能会发生杠杆系统之间或与其他试验设施之间的干涉现象，进而影响到整个试验进程。因此，有必要预测出结构大变形情况下杠杆系统的位移，并进行干涉情况检测，这对机翼结构验证技术的发展有重要意义[9]。

本文对杠杆系统进行受力分析，建立描述结构静力试验中机翼变形后杠杆系统位置方程组，求解出机翼结构发生大变形情况下杠杆组的位移，进一步可分析出随动加载方式下的杠杆位移。另外在巴塔西等[8]的基础上开发了机翼变形情况下的杠杆组系统CATIA参数化建模软件，可用于试验杠杆组设计。

1 杠杆系统位移求解模型

1.1 单个杠杆位置方程组

采用杠杆系统对飞机结构表面施加载荷时，将机翼表面上的两个加载点用加载杠杆连接起来。根据杠杆原理，按两个加载点分配的载荷大小计算出杠杆上的合力点位置，再使用高一级的杠杆给两个合力点施加载荷。故杠杆系统最基础的结构由两个加载点、杠杆、杠杆合力点、连杆与加载点的绳索组成。杠杆加载系统与结构表面加载点的定义如图1所示。

第i号杠杆进行受力分析见图2，其两端点为点i1(xi1,yi1,zi1)和点i2(xi2,yi2,zi2)，上级杠杆的一个端点为h1(xh1,yh1,zh1)。杠杆端点坐标在初始状态下

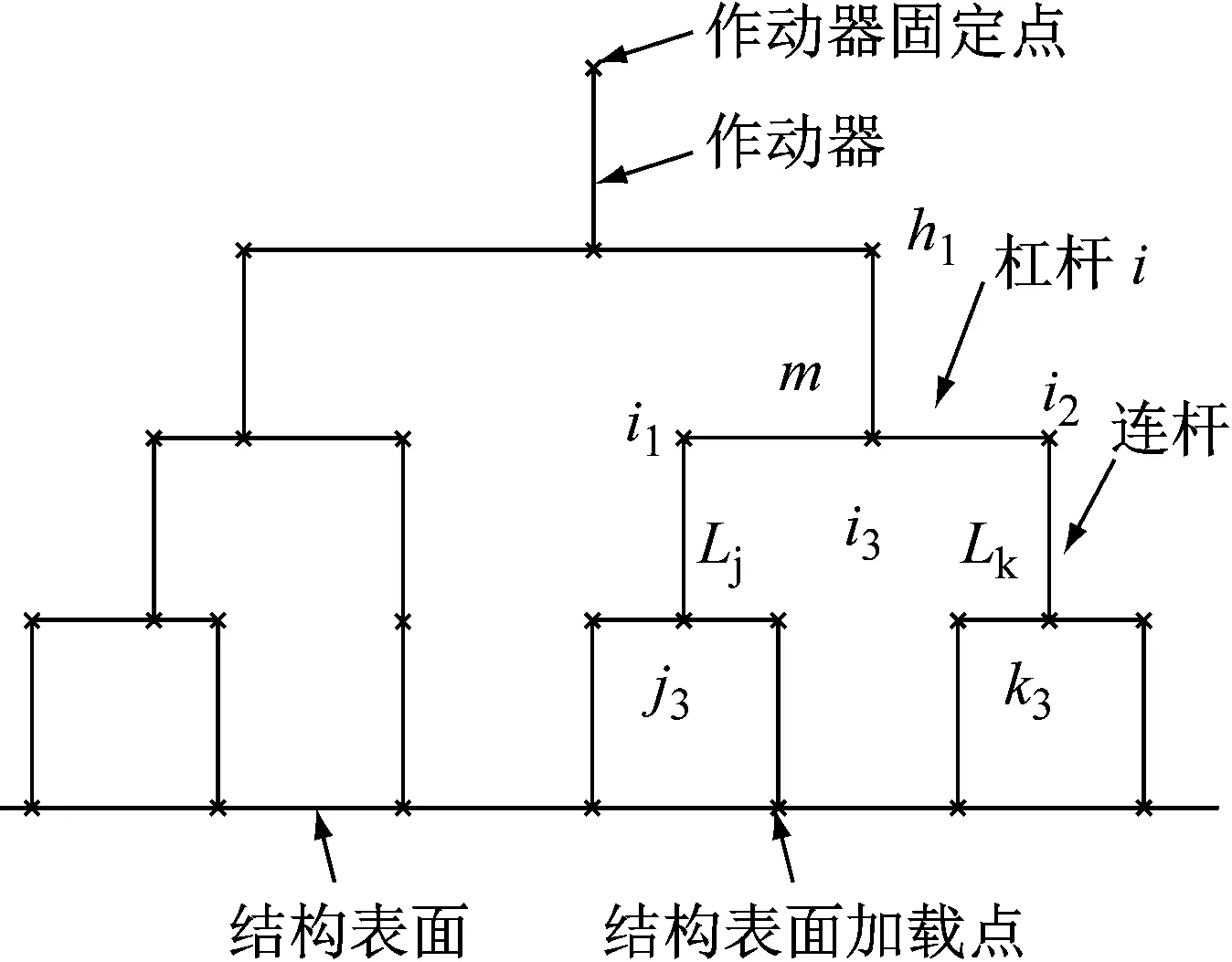
图1 杠杆系统示意图

为已知量，在结构表面发生变形后为待求量。杠杆中点距离两端点的长度分别为m和n，在试验方案确定情况下为确定值；杠杆上合力点为i3，其坐标为:

(1)

线段i1j3和i2k3分别代表杠杆的两个端点与低一级杠杆j和杠杆k中间点的连杆，其长度分别为Lj和Lk，在加载过程中保持不变。

图2 杠杆i受力示意图

结构静强度试验中杠杆和连杆(连接杠杆端点和加载点的吊索)变形可以忽略不计，故可作为刚体简化，其长度不变，可以得到:

(2)

在该杠杆系统的基本单元中，点i1、i2、j3、k3如不在同一平面内，杠杆两端力矩不平衡，将产生扭矩将4点扭回同一平面内，所以这4点必定在同一平面内，由i1i2、i1j3、i2k3这3条线段在一个平面内的条件可得：

(3)

再通过力的平衡关系建立方程，引入向量i1j3、i2k3及其单位向量a、b

引入系数R作为两个连杆i1j3、i2k3作用于杠杆上力的大小比值，当两个连杆平行时，其值即n和m之比，当连杆不平行时，则由力矩平衡得到：

再引入向量v1和v2。v1代表两连杆上合力矢量(见图2);v2代表合力点与上一级杠杆端点的连接方向，则有:

v1=Ra+b

(12)

(13)

由三力平衡关系，两连杆上力的矢量和方向与i3h1共线，得到最后一个约束方程：

v1×v2=0

(14)

方程组(2)、(3)以及式(14)给出了杠杆系统最基本单元的运动约束。以此为基础，进一步考虑多个杠杆组合的情况。

1.2 杠杆系统位移方程组

在结构静力试验中，通常有多个作动器对结构施加载荷，每个作动器下有一组杠杆，但各个杠杆组是独立的，因此只求解一个作动器下杠杆组的位移。

对每一个杠杆可以建立一个由式(2)、(3)和(14)构成的方程组。参考图1，对第1级杠杆而言，j3、k3点是机翼结构表面的加载点，合力点i3是第2级杠杆的加载点，h1是第2级杠杆的端点。以此类推，最后一级杠杆的h1点就是作动器的悬挂点。由力学推导可知，式(14)中系数R获得建立在式(3)共面约束的基础上，如果在方程组中去掉式(3)易导致式(10)中R取值错误，影响方程组的求解。所以，对单个杠杆，未知数的数目为6，但可以构建得到7个方程。假设系统共有p个杠杆，则方程总数为7p。令第i号杠杆的位移方程组为{f}i={0}(i=1,2,…,p)，则整个杠杆系统的位移方程组为：

{{f}1={0}…{f}i={0}…{f}p={0}

(15)

整个杠杆系统中，单个杠杆的几何参数,即m和n是定值，结构表面加载点坐标和作动器悬挂点坐标的初值是已知量；加载过程中，各个载荷下的结构表面加载点的坐标由结构分析得出，在模拟计算中作为已知量；如果是随动加载，各载荷状态下的作动器悬挂点的坐标也是作为已知量；加载过程中每一个杠杆两个端点坐标是待求的未知量。结构表面点和作动器悬挂点的坐标发生变化后，对式(15)的平衡产生扰动，求解每个杠杆两端点的坐标值，使式(15)平衡，即得到对应载荷下杠杆系统的位移。

式(15)是一个多元非线性方程组，本文采用Levenberg-Marquardt算法求该方程组的数值解，获得每一个杠杆端点的坐标。该算法能提供非线性最小化(局部最小)的数值解，通过执行时修改参数达到兼具高斯-牛顿算法以及梯度下降法的优点，并对两者之不足作了改善(比如高斯-牛顿算法之反矩阵不存在或是初始值离局部极小值太远)[10-11]。Matlab内置函数fsolve解方程函数就使用了这种算法。

1.3 机翼大变形情况下杠杆位移的求解

模拟机翼大变形情况时，直接将大变形状态下机翼表面加载点坐标代入式(15)容易导致计算结果不准确或者得不到收敛解。为得到较为精确的模拟结果，需将表面加载点逐步移动至最终状态，即模拟实际情况下静力试验中逐步加载载荷，通过不断迭代获得大变形下杠杆系统位移，计算流程如图3所示。

图3 计算流程图

机翼大变形过程中，其气动压力中心会随机翼变形发生变化，为了更真实地模拟飞行状态下翼面的受载历程，可采用随动加载方案，保证载荷大小和方向接近于真实状态[12-13]。随动加载方式在整个结构试验过程中，通过改变作动器的位置，使得机翼表面载荷的压心发生移动。计算思路可在机翼大变形情况基础上，将结构当前变形下作动器坐标输入到方程组中，按图3中的计算流程可得到随动加载情况下杠杆系统的位移。

2 杠杆系统几何模型的参数化建模

使用CATIA二次开发功能对加载杠杆进行建模，CATIA提供了多种二次开发的接口，应用最多的主要有两种方法。① 开放的基于构件的应用编程接口CAA V5技术;② 自动化对象编程CATIA Automation技术[12]。这些接口给用户提供了一系列工具，可以完成宏程序执行、用户界面定制以及模型生成等功能。

本文采用Automation API技术对CATIA进行二次开发。Automation API是CATIA预先编好的一组函数，用于与外界进行通信。在MS-VB环境下进行CATIA二次开发时，需先连接CATIA的API，连接后就可以直接调用CATIA中API的函数进行相关程序的编译。

使用VB开发的加载杠杆系统建模软件的操作界面如图4所示。

图4 杠杆建模操作界面

建模过程主要分为3个步骤：

(1) 数据输入。输入数据由表面点数据和杠杆点数据组成。机翼表面加载点的数据包括点的编号和点的3个坐标，如表1所示。表2中数据均为第1级机翼杠杆数据，例如编号为101的杠杆，其两端点编号分别为1001和1002，第4～第6列给出该杠杆中间连接点的坐标以及其m，n的数值。

表1 表面点数据表 mm

(2) 杠杆零件生成。通过第1步中杠杆m、n等数据输入，可以批量生成各个杠杆。并由连接点的坐标位置可以建立各杠杆的装配关系模型。图5给出了一个杠杆的模型和初始状态下一组杠杆几何连接关系模型。

(3) 模型装配。装配关系主要由3个约束确定：

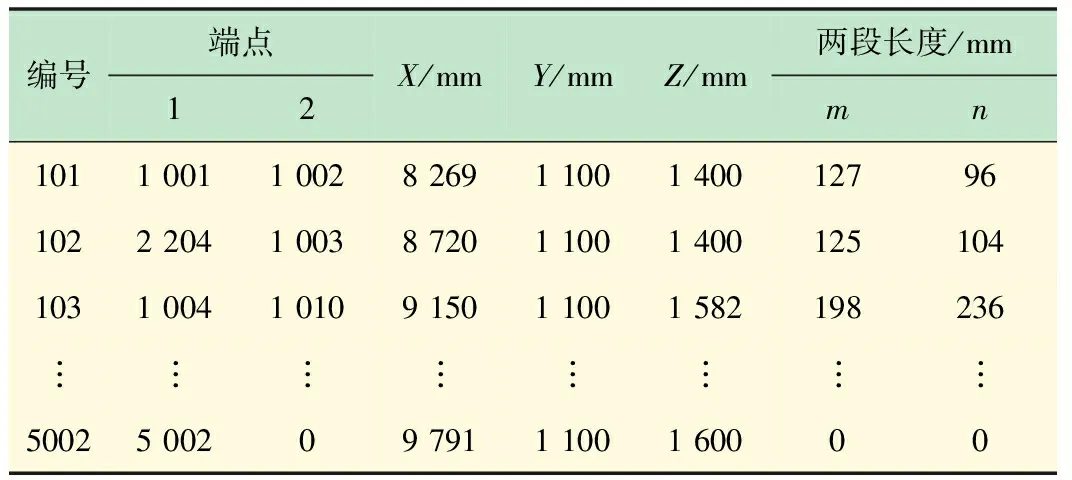
表2 一级杠杆点数据格式定义

(a) 杠杆模型

(b) 杠杆几何装配关系模型

杠杆模型中连接点与关系模型中对应点相合，杠杆零件轴线与杠杆装配关系模型中对应线段重合，以及杠杆中间螺栓的轴垂直于杠杆装配关系模型的连杆。图5(a)为杠杆零件模型，图5(b)为杠杆装配关系模型。通过装配功能，最终得到图5(c)所示的加载杠杆组的整体模型，此时模型处于初始状态，各杠杆于连杆保持垂直。表1中显示的就是该图中杠杆组的部分数据。

3 杠杆组位移计算和参数化建模算例

3.1 机翼表面加载点位移拟合

杠杆组模拟计算前应获得特定翼面的变形数据。为了计算的简便，本文假设机翼表面的变形满足等截面悬臂梁受到均布载荷时发生的变形。将假设的模型沿x轴方向分为t等分，每一等分的两端截面分别记作M、N(见图6)。当在T截面施加集中力F时，MN段变形到M′N′位置，N截面的位移有δ1、δ2、δ3三部分组成，δ1是由M截面的变形而产生的牵连位移，δ2是假设MN段是刚性不变形的情况下,M截面转过一定的角度之后N截面产生的位移，δ3是假设M截面固支的情况下,N截面受集中力之后的位移。

图6 等剖面悬臂梁[15]

于是对于悬臂梁的第t段，受载的一端和另一端的位移之差为：

yt-(t-1)=θt-1lt+yt

(16)

(17)

式中,载荷力F、E和惯性矩I假设均为常量。对式(16)积分可以拟合得到一条近似的机翼挠曲线。给定机翼末端最大变形数值，即可以模拟机翼表面各点的位移情况。使用图5(c)中的杠杆组作为算例，假设翼梢上翘位移500 mm，此时各点的位移如表3所示，作动器初始坐标位于最高一级杠杆连接点正上方1 m，随试验加载逐步沿展向(表中Z方向)移动249 mm。表3给出拟合后各表面点Y方向位移数值。

表3 翼梢上翘500 mm后表面坐标

3.2 CATIA杠杆变形拟合结果

由表1～3的数据作为输入，位移分为1 000步，通过Matlab程序计算可以得到机翼在大变形随动加载情况下杠杆组位移情况。图7所示通过Matlab绘图功能展示了机翼变形前后杠杆组位移情况。

(a) 侧视图

(b) 等轴视图

将该结果所得的杠杆信息以及坐标位置作为数据输入图4所展示的CATIA二次开发软件中，自动生成并装配得到机翼大变形情况下杠杆组的几何模型，如图8所示。与图7(a)Matlab的侧视图模型相比较，图8所示的杠杆组信息和坐标位置一致，表明CATIA二次开发软件模型建立正确。该结果是在方程组求解迭代收敛前提下得到的，说明满足方程约束条件。