双向偏心受压支座锚栓的简化计算方法
2019-09-03魏忠
魏 忠
(中国建筑西南设计研究院有限公司, 四川成都 610042)
支座锚栓的计算方法在现行规范中没有明确规定。国内外对单向偏心受压支座锚栓的设计基于不同的假定,有大约十种计算方法[1],其计算结果差异较大;对于双向偏心受压支座锚栓则没有成熟可靠的计算方法。随着空间结构越来越多的运用,结构中支座锚栓基本为双向偏心受压,设计时只能凭经验将轴压力分解到两个方向按单向偏心受压计算,再将锚栓面积进行叠加,其计算依据不足。为了能合理并快速地进行双向偏心受压支座锚栓的设计,本文提出了一种计算方法,可以方便地进行手算。
1 单向偏心受压支座锚栓的计算
目前国内工程设计实践中,对单向偏心受压支座锚栓的计算一般采用弹性设计,主要有以下三种方法。
1.1 弯矩平衡法
此方法在我国TJ 17-74《钢结构设计规范》中有明确规定,但在修订后的GBJ 17-88《钢结构设计规范》中及最新版的GB 50017-2003《钢结构设计规范》中均取消了此规定。这种计算方法简单方便,在设计中得到了较广泛的应用。
此方法假定支座底板与混凝土顶面的压应力为线性分布(图1)。
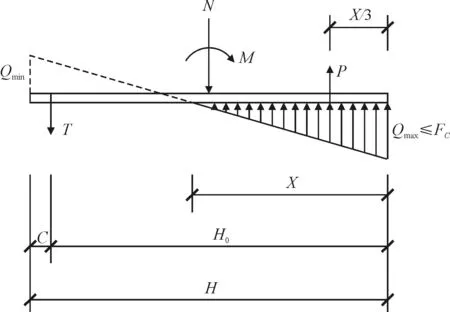
图1 锚栓计算简图一
可得:
(1)
(2)
式中:N、M为作用于底板形心轴处的轴压力(N)和弯矩(N·mm);B、h为底板宽度(mm)和长度(mm);fc为混凝土的轴心抗压强度设计值,当允许计入局部承压提高系数时以βfc代替。
当σmax小于0时,按下式确定混凝土受压区高度x:
(3)
根据弯矩平衡条件:
(4)
将式(3)代入式(4)中可求得锚栓拉力T。
此方法仅有单一未知数,求解简单,但不满足竖向力的平衡条件,且计算结果偏大,某些情况下显得不合理。
1.2 力与弯矩平衡法
此方法假定支座底板下混凝土应力分布为三角形,并取混凝土最大应力σmax=fc(图2)。
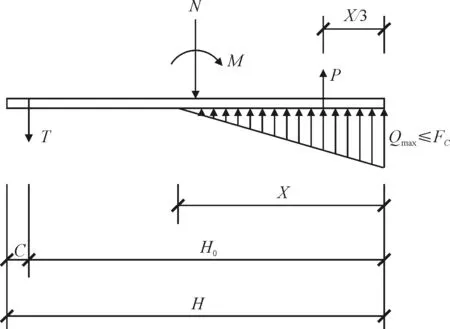
图2 锚栓计算简图二
由竖向力和力矩平衡条件,可得:
(5)
(6)
式中:P为混凝土受压区压力的合力(N)。
联立式(5)、式(6),解二次方程可得支座受压区高度x,代入式(5)中即可求出锚栓拉力T。
此方法满足两个静力平衡条件,仅需解一个联立方程,较为简单,结果比较合理,推荐使用。
采用无量纲形式,令:
由式(5)、式(6)可得:
(7)
1.3 平截面假定下的力与弯矩平衡法
此方法引入平截面假定,计算简图见图3。

图3 锚栓计算简图三
由平衡关系可得:
(8)
(9)
其中:
σc=Ecεc
(10)
σs=Esεs
(11)
式中:σc、σs为混凝土和钢筋的应力;εc、εs为混凝土和钢筋的应变;Ec、Es为混凝土和钢筋的弹性模量。
由平截面假定可得:
(12)
以上各式联立组成方程组,需要解关于x的三次方程,再求得锚栓拉力T。
此方法从理论上讲更为精确和合理,求得的锚栓面积较小。《钢结构设计手册》[2]中对按前两种法计算出的锚栓直径大于60 mm时,推荐采用此计算方法,但计算较为繁琐,需借助编程或表格求解。
其余单向偏心受压支座锚栓的计算方法不再赘述,综合考虑在工程设计中推荐使用第二种方法。
2 双向偏心受压支座锚栓的计算
对双向偏心受压支座锚栓的计算,可参照钢筋混凝土双向偏心受压构件的情况进行分析和简化近似计算(图4)。

图4 双向偏心受压截面
钢筋混凝土双向偏心受压构件的破坏曲面如图5所示,其等轴力线近似为一内凹的椭圆,即曲线方程的指数α小于2(椭圆方程指数为2),一般可表示为下面的无量纲形式:
(13)
式中:Mx、My为轴力N作用下截面的双向偏心破坏弯矩M在x、y轴方向上的分量;Mnx、Mny为轴力N作用下截面的单向偏心破坏弯矩。
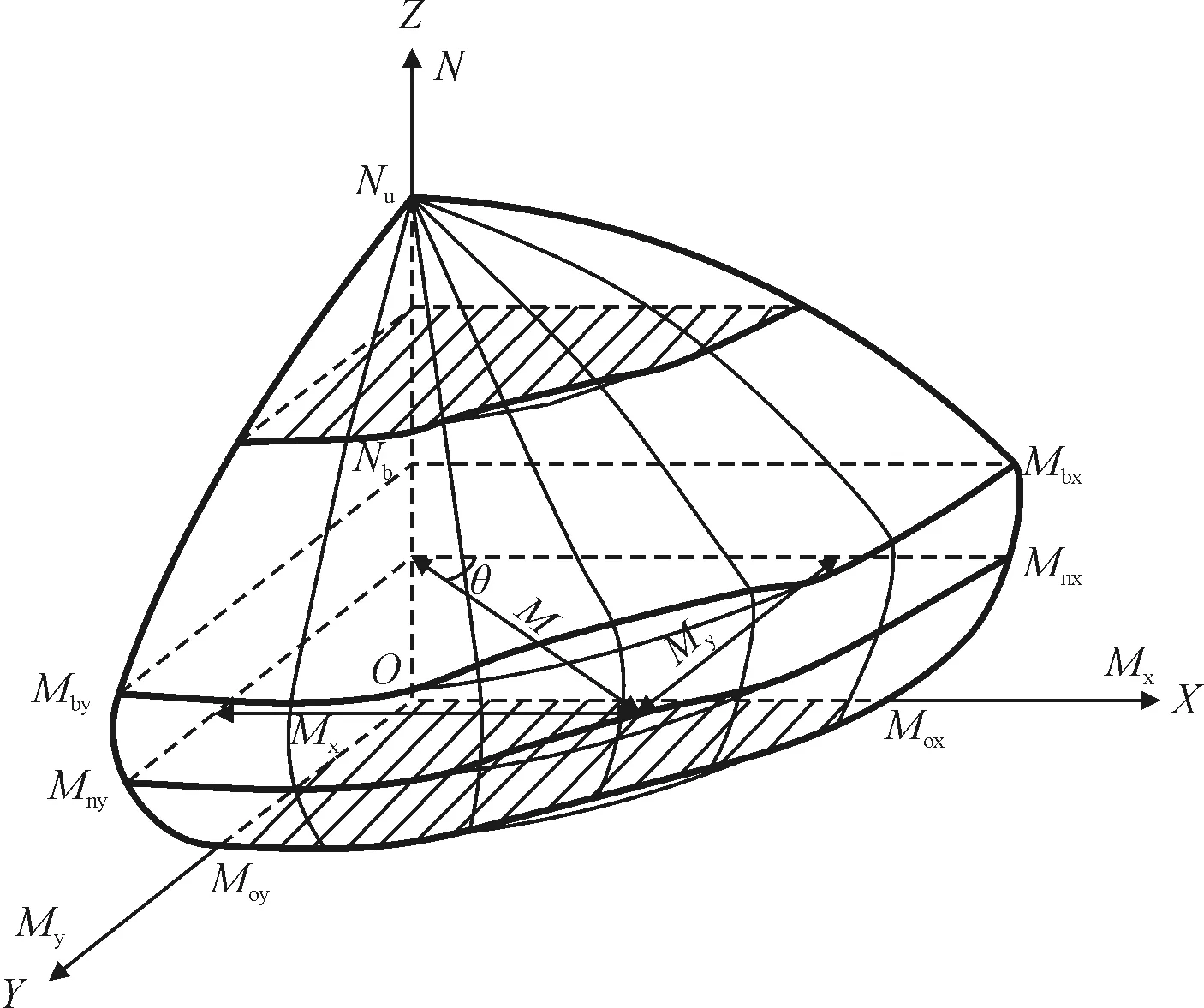
图5 双向偏心受压破坏曲面
周边均匀配筋的环形或圆形截面,其等轴力线为圆,但对称配筋的方形截面,其等轴力线是比圆凹进一些的曲线。当轴力作用在截面的对角线上时,与圆的偏离最大。同样,矩形截面双向偏心受压构件N-M相关曲面的等轴力线也不是椭圆,当轴力作用于对角线上时,它与椭圆曲线的偏离最大。当轴压力为0时,等轴力线与椭圆的偏离很小,即α接近2.0。随着轴压力的增大,等轴力线与椭圆的偏离逐渐增大,当N=Nb,即界限破坏时,等轴力线与椭圆的偏离达到最大值。当轴压力趋近于轴心受压的轴力Nu时,偏离逐渐消失[3]。
由图5可知,在某一给定轴力N作用下,双偏压内力组合(Mx,My)与两个方向的单偏压内力组合(Mnx,0)或(0,Mny)具有相同的截面配筋。因此,通过将双偏压的内力转化为两个单偏压内力,再分别进行截面的单偏压计算,就能比较方便快捷地得出配筋结果。另一方面,截面配筋不同,破坏曲线也不同,从理论上讲,过点(N,Mx,My)的破坏曲线可以有无数条,因此将Mx、My换算得到的Mnx、Mny也有无数组,可以分别求得对应的不同配筋。对换算结果产生影响的两个因素是曲线方程中的α以及比值Mnx/Mny,以下先对α的取值进行分析。
欧洲规范EN 1992-1-1:2004[4]规定:对于圆形和椭圆形截面α=2.0,对于矩形截面根据轴压比按表1取值。

表1 EN1992-1-1:2004矩形截面的α值
其余轴压比情况可按表1进行插值,或按下式确定:
α=0.926n2+0.093n+0.981
(14)
国内许多学者对α的取值进行了深入研究,一般是以GB 50010-2010《混凝土结构设计规范》[5]附录E的方法为标准,通过数值计算,回归拟合出满足式(13)的α值,其结果基本相似[6-7],如图6、图7。
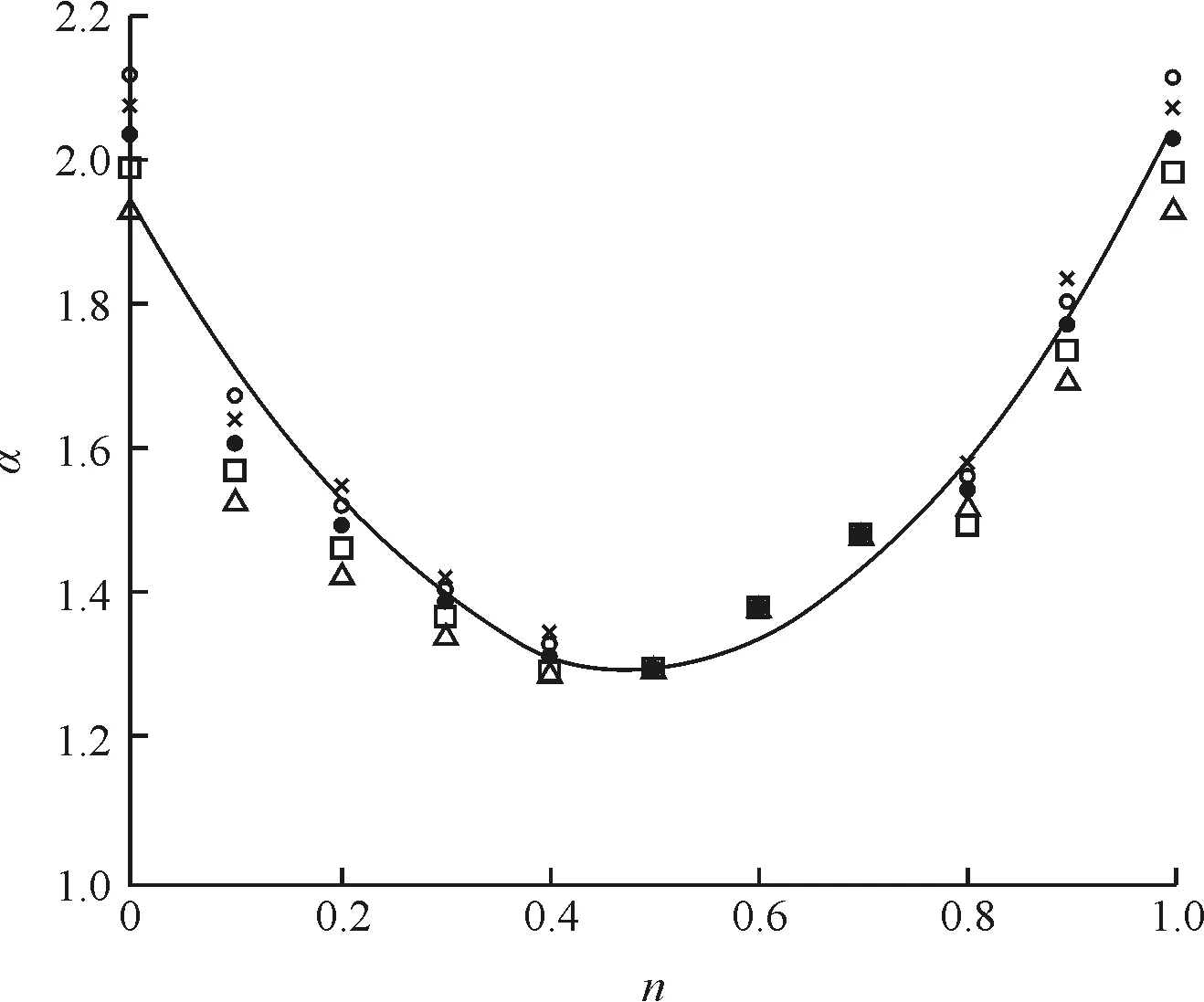
图6 α-n数据点及拟合曲线
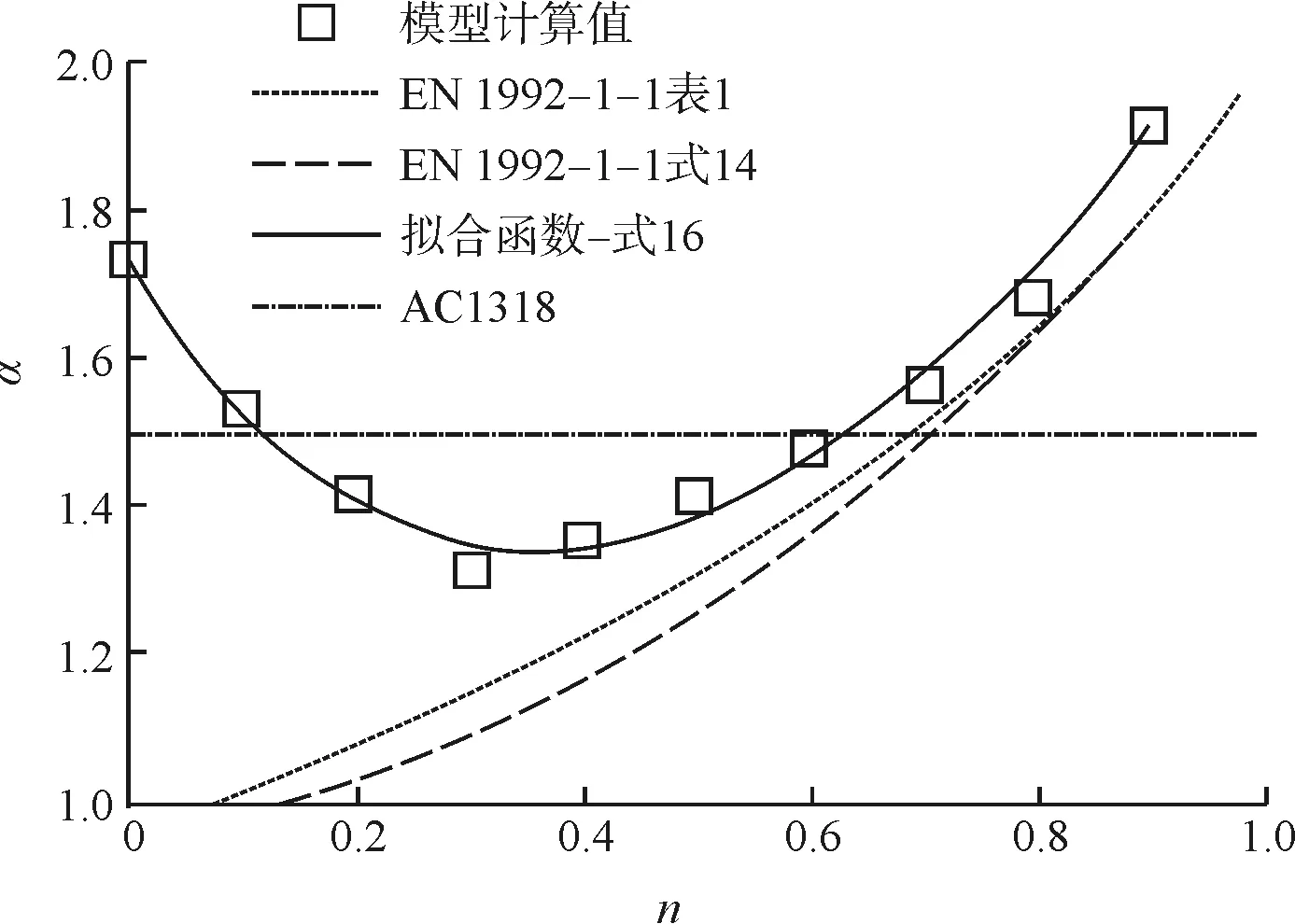
图7 α-n拟合曲线及对比结果
图6对应的拟合曲线函数为:
α=2-3n+3n2
(15)
图7对应的拟合曲线函数为:
α=1.74-2.91n+7.33n2-7.57n3+3.59n4
(16)
可以看出:与文献[3]中描述相似,α的最小值在大小偏压界限点附近取得;在小偏压阶段α值与欧洲规范EN 1992-1-1:2004[4]相似;但在大偏压阶段,曲线相差较大。这种大偏压下的偏离现象在Shin、Fossetti及Bajaj等的文献中也有出现。
综上,在锚栓的简化计算中建议α按表2取值。

表2 锚栓简化计算中的α值
其余轴压比情况可按表2进行插值。
为了将双向受压转化为单向受压以便于计算,可将双向受压的弯矩M分别投影到OXZ和OYZ平面,如图5,得到Mx和My,再将Mx和My分别乘以适当的放大系数Kx和Ky,将弯矩放大至单偏压破坏曲线上的Mnx和Mny,分别对两个方向按内力(N,KxMx)和(N,KyMy)进行单偏压计算,即可得到两个方向的锚栓计算面积。
令m=My/Mx,与式(13)联立,容易推出:
(17)
(18)
式中:μ为轴力N作用下支座截面两个方向的抗弯承载力之比,按下式确定:
(19)
单偏压破坏曲线上轴向力为N时的截面抗弯承载力Mnx或Mny可按下列公式计算:
当N≤ξbfcbh0时,
(20)
当N>ξbfcbh0时,
(21)
(22)
式中:ξb为相对界限受压区高度。
由式(5)可知,在锚栓设计中,N≤0.5fcbh0,否则锚栓将受压,按构造设置即可。而ξb>0.5,因此Mnx或Mny的计算采用式(20)。
在锚栓面积未知的情况下无法求得截面抗弯承载力Mnx或Mny,此时可采用如下方法对μ进行近似计算。因等轴力线在OXY平面的投影近似为相似的曲线,即Mnx/Mny的值基本不变,所以可以用轴向压力N=0时双向受弯构件的抗弯承载力比值Mox/Moy近似,即:
(23)
式中:Asx、Asy为支座截面x、y方向的单侧锚栓面积。
(24)
(25)
可以看出,当b与h相差不大时,γb≈γh。
一般情况下支座锚栓均为相同规格,此时式(23)可进一步简化为:
(26)
式中:nx、ny为支座截面x、y方向的单侧锚栓个数。
计算时假定锚栓取相同规格,根据支座每边预设的锚栓数量即可按式(26)求得μ值。考虑到计算比值μ时分子分母舍了相同的项γbN(γhN),为使μ值计算相对更准确,当ny
因为μ值是近似计算得出的,所以按照上述方法计求得的x、y两个方向的锚栓面积比与预设的锚栓面积比不一定相同。因为双偏压的计算结果有多解,按此结果(或取大值)配置锚栓是可行的。若想得出与预设的锚栓面积比更接近的计算结果,可以根据计算结果对μ值乘以修正系数ku,得到修正后的μ值,按上述步骤重新计算一次。一般情况下只需重算一次即可得出与预设的锚栓面积比相近的结果。修正系数ku按下式确定:
(27)
式中:Asx、Asy为计算得出的支座截面x、y方向的单侧锚栓面积。
3 计算实例
根据以下数据进行双向偏心受压支座锚栓的计算:
柱脚底板尺寸:b=540mm(x方向),h=800mm(y方向)。
混凝土采用C30,fc=14.3N/mm2,不计局部承压提高系数;锚栓采用Q345,fta=180N/mm2;asx=90mm,asy=100mm。
内力1:N=921kN,Mx=208kN·m,My=552kN·m,Vx=86kN,Vy=152kN。
内力2:N=465kN,Mx=208kN·m,My=552kN·m,Vx=86kN,Vy=152kN。
单向受弯锚栓的计算均采用前述1.2的方法。
方法1先在x方向考虑轴力N和弯矩Mx的作用进行锚栓计算,然后在y方向仅考虑弯矩My的作用进行锚栓计算,再将两次的计算结果相加求得锚栓面积。
方法2先在x方向仅考虑弯矩Mx的作用进行锚栓计算,然后在y方向考虑轴力N和弯矩My的作用进行锚栓计算,再将两次的计算结果相加求得锚栓面积。
方法3先将轴力N按x、y向的剪力Vx、Vy的比值分解为Nx、Ny,然后在x方向考虑轴力Nx和弯矩Mx的作用进行锚栓计算,在y方向考虑轴力Ny和弯矩My的作用进行锚栓计算,再将两次的计算结果相加求得锚栓面积。
方法4采用本文推荐的简化计算方法。采用本文方法进行计算的过程如下:
轴压比:
由表2得:α=1.55。
支座每边设置3颗锚栓,即nx=ny=3,可得:
另可得:
则:
于是:
Mnx=KxMx=2.056×208=428kN·m
Mny=KyMy=1.254×552=713kN·m
取N=921kN、M=457kN·m和N=921kN、M=692kN·m分别按1.2中的方法进行两个方向的锚栓计算,即可得到表3方法4括号中的锚栓面积。计算结果见表3、表4。
方法4括号中的锚栓面积为只进行第一次计算的结果,对μ值进行修正后得到最终锚栓面积,结果相差并不大,因此只进行一次计算一般情况下是可行的。

表3 不同计算方法下的双向偏心受压支座锚栓面积(内力1)
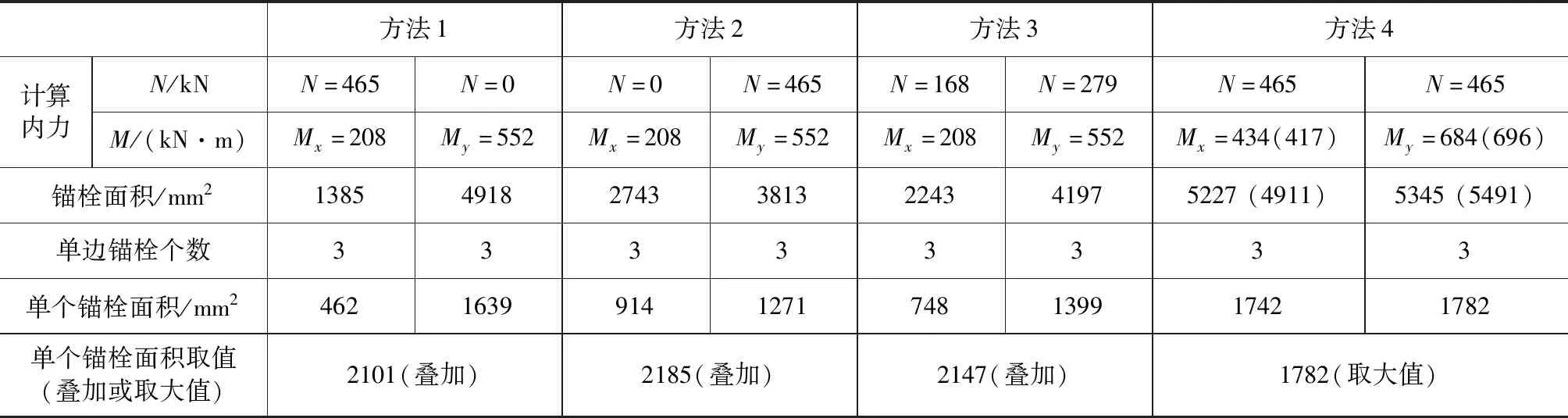
表4 不同计算方法下的双向偏心受压支座锚栓面积(内力2)
由表中可见,本文推荐的方法比常规的分解算法得到的锚栓面积小10 %~20 %,经济性更好,而且有理论依据。
4 结束语
目前国内工程设计中对双向偏心受压支座锚栓的计算没有简便而又有可靠根据的算法,本文通过对钢筋混凝土双向偏心受压构件受力特性的分析类比,推导出了一个较简便的计算方法,可以通过手算快速进行计算,得出的锚栓面积更为经济合理。
需要指出的是,由于国内工程设计中锚栓一般采用弹性设计,其混凝土的应力分布为三角形,且锚栓应力未考虑变形协调,因此本文提出的计算方法只是一种近似算法,但用于工程设计是可行的。
致谢:成文过程中,中国建筑西南设计研究院有限公司副总工程师刘宜丰提出了很多宝贵意见,特此致谢。
