页岩气压裂水平井控压生产动态预测模型及其应用
2019-09-03贾爱林位云生王军磊齐亚东贾成业
贾爱林 位云生 刘 成 王军磊 齐亚东 贾成业 李 波
1.中国石油勘探开发研究院 2.中国石油浙江油田公司 3.华能国际电力开发公司
0 引言
通常认为页岩气井产能下降是由于储层应力敏感导致介质传导能力下降而造成的[1-3]。根据有效应力与原地应力、孔隙压力之间的函数关系[4]可知,随着页岩气井的生产,地层压力逐渐衰减,地层/裂缝受到的有效应力逐渐增加,由于裂缝中支撑剂流失、嵌入和被压碎,页岩气流动的通道发生变形,导致其渗流能力降低。页岩气的开发实践表明,控压限产的生产方式可以有效提高页岩气最终可采量(以下简称为EUR)[5-7]。在北美地区,相比于Barnett、Marcellus等页岩气藏,Haynesville页岩由于地层压力较高,储层应力敏感性特征显著,在气藏的实际开发过程中广泛采用控压限产的生产方式,实践证明该方式较放压生产方式,单井EUR可普遍提高28%[8];国内长宁—威远、昭通等页岩气示范区的地质条件与Haynesville页岩气藏相似,经过几年的现场试验后也逐步在推广控压限产的生产方式[9-10]。
与放压生产相比,控压限产有利于降低压裂液返排率,更重要的作用在于保持人工裂缝的长期开启,缓解渗流场的应力敏感效应[4,11]。裂缝系统的应力敏感效应直接受有效应力场控制,当原地应力场的变化幅度很小时,利用线性关系,有效应力可近似转换为孔隙压力,将压力场的模拟结果与应力敏感曲线相结合可用于气井生产动态的分析[12-14],该方法虽简洁有效,但有效应力估计值偏低,导致单井EUR预测值偏高,同时由于无法模拟井底压力对有效应力场的直接影响,使得放压和控压两种生产方式所引起的产量差异不明显。尤其对于页岩等非常规储层,压力场变化会引起原地应力场发生显著变化,国内外学者较多利用流固耦合数值模型[4,15-16]、应力解析模型[17-18]来精确表征生产过程中压力场—应力场的耦合变化,虽然能模拟不同控压制度下单井的开发指标,但模型过于复杂且计算代价巨大,难以推广应用。
为了理清页岩气压裂水平井采取控压生产制度延缓裂缝闭合与提高单井EUR的内在联系,明确控压生产的气藏工程意义,笔者以有限导流裂缝为基本流动单元,引入变应力敏感系数,建立地层—裂缝耦合的压裂水平井生产动态预测模型并求解,并与经典模型、Saphir软件数值模型的计算结果进行对比,在此基础上,采用所建立的模型分析了应力敏感性特征参数、控压生产制度等因素对压裂水平井生产动态的影响,进而对某两口实例井在不同控压制度下的生产动态进行拟合和预测。
1 裂缝—地层耦合流动模型
1.1 假设条件与参数
水平井进行水力压裂改造后,流体从地层到井筒的流动分为从地层到裂缝和裂缝内部这两个部分。裂缝与地层中的流量及压力在裂缝壁面处相等,由此将这两个部分流体的流动进行耦合,然后通过计算得到不同时刻地层中任一点的压力。具体假设如下:①矩形地层均质、等厚,四周及上下均封闭;②压裂裂缝纵向上穿透地层,裂缝垂直于水平井筒且关于井筒呈不对称分布,且由跟端到趾端依次排列第1, …, n,…, nf条裂缝;③气井以定井底压力进行生产,整个流动过程均符合达西定律,不考虑井筒管流的影响;④气井生产引入拟压力,将气体流动问题等效转换为液体流动问题;⑤考虑人工裂缝具有强应力敏感性,未考虑储层基质的应力敏感性[4-6]。
拟压力表达式为:
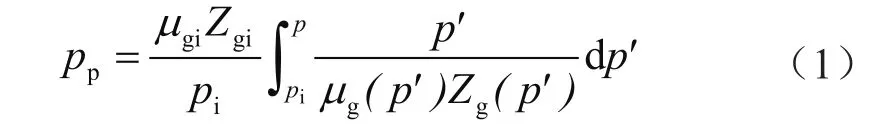
式中pp表示拟压力,Pa;μg表示气体黏度;Pa·s;Zg表示气体偏差因子;p表示地层压力,Pa;p'表示压力积分符号,Pa;下标i表示初始状态。
相对于渗透率的应力敏感性,孔隙度的应力敏感性通常可忽略[19]。随着裂缝承受的有效应力不断增加,裂缝发生闭合,渗透率/导流能力降低,这里设定裂缝渗透率与有效应力呈指数关系,如式(2)所示;同时,由于不同区域有效应力变化的速率不同,导致裂缝的闭合程度也不同,且随时间变化裂缝的导流能力将发生变化。
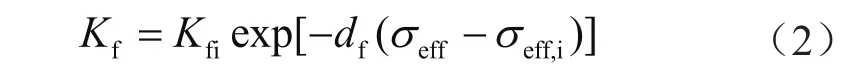
式中Kf表示裂缝渗透率,1012D;df表示渗透率模量,Pa-1;σeff表示有效应力,Pa;下标f表示裂缝。
由于裂缝壁面粗糙度较大,即使裂缝已经不再随有效应力增加而闭合,裂缝仍具有一定渗流能力,此时所对应的最小裂缝渗透率(Kf,min)仍远高于基质渗透率[20]。将式(2)改写为:
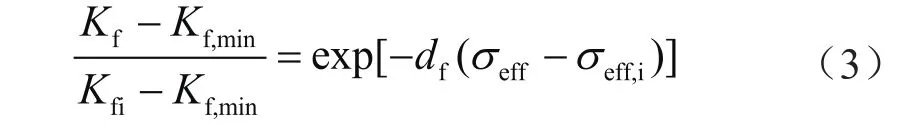
式中下标min表示最小值。
为方便与渗流模型相结合,需将式(3)与孔隙压力建立起函数关系。由于有效应力、原地应力和孔隙压力满足的关系式为:

式中σ表示原地应力,Pa;α表示Biot系数。
应力差与孔隙压力差的关系式为[17]:
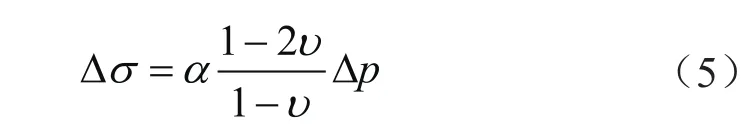
式中υ表示泊松比。
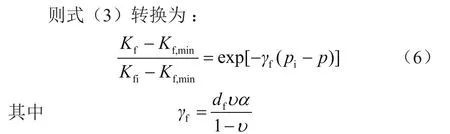
式中γf表示应力敏感系数。
df为常量或是与有效应力相关的变量,具体形式取决于介质类型。通常,对于硬地层,df为常量,而对于软地层,df则为变量。Alramahi和Sundberg[20]提供了不同硬度地层中裂缝导流能力的实验数据,并进行最优拟合,结果显示对于硬地层,裂缝渗透率的自然对数与有效应力呈线性关系,而对于软地层,二者满足二项式关系。由长宁地区龙马溪组页岩人工裂缝的应力敏感性实验的测试结果,显示裂缝渗透率的自然对数与有效应力满足二项式关系(图1),渗透率模量是有效应力的函数,而不是常量。
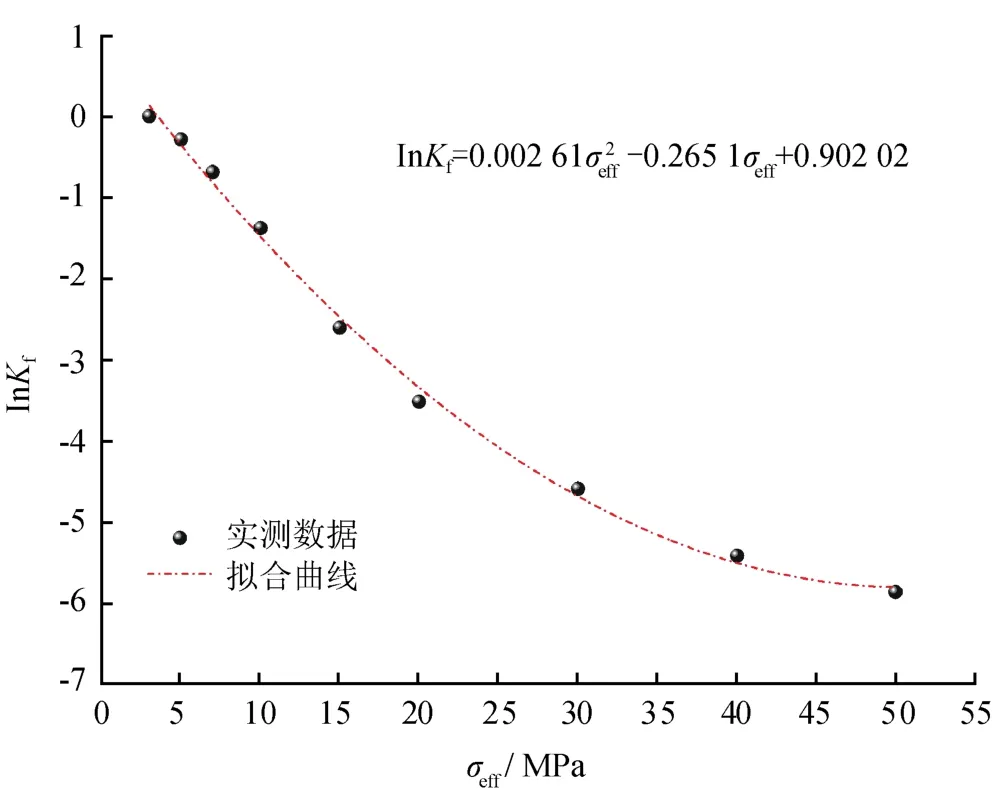
图1 Kf与σeff的半对数拟合曲线图
基于渗透率模量与有效应力的函数关系式,再结合有效应力与孔隙压力的关系式,应力敏感系数的表达式可转换为:

式中a、b分别表示应力敏感特征系数;pf表示裂缝压力,Pa。
为便于研究,定义无量纲时间(tD)、裂缝长度(LD)、导流能力(CfD)和应力敏感系数(γfD),具体表达式为:
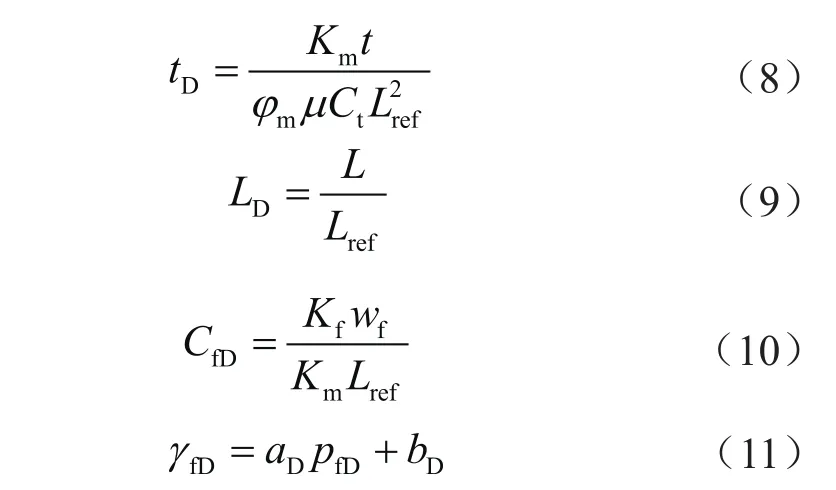
式中Km表示储层渗透率,1012D;t表示时间,s;φm表示储层孔隙度;μ表示流体黏度,Pa·s;Ct表示综合压缩系数,Pa-1;Lref表示参考长度,m;L表示裂缝长度,m;wf表示裂缝宽度,m;aD、bD分别表示无量纲应力敏感特征系数;下标D表示无量纲。
在定产量条件下,针对裂缝无量纲压力(pfD)、应力敏感系数(γfD)、流量(qwfD)及流量密度(εfD)的定义式为:
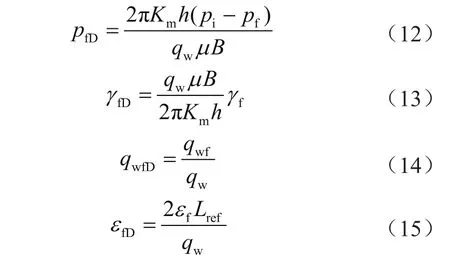
式中h表示储层厚度,m;qw表示水平井流量,m3/s;B表示流体体积系数;qwf表示裂缝流量,m3/s;εf表示裂缝流量密度,m2/s。
在定井底压力条件下,针对裂缝无量纲压力、应力敏感系数、流量及流量密度的定义式为:
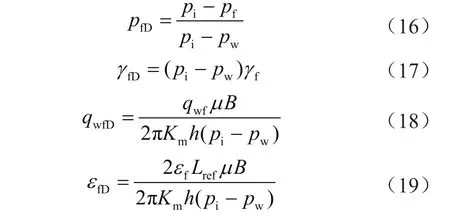
式中pw表示井底压力,Pa。
对于气井生产而言,需将式(12)、(16)~(19)中的压力替换为拟压力,相应式(8)、(12)、(18)~(19)中的 μ、B 替换为 μgi、Bgi。
1.2 数学模型的建立
地层中流体在裂缝中的流动为变流量密度线性流,而后由裂缝汇入到井筒中的流动为近井筒径向流。因此,可将裂缝和井筒视为两个独立的流动空间(图2)。
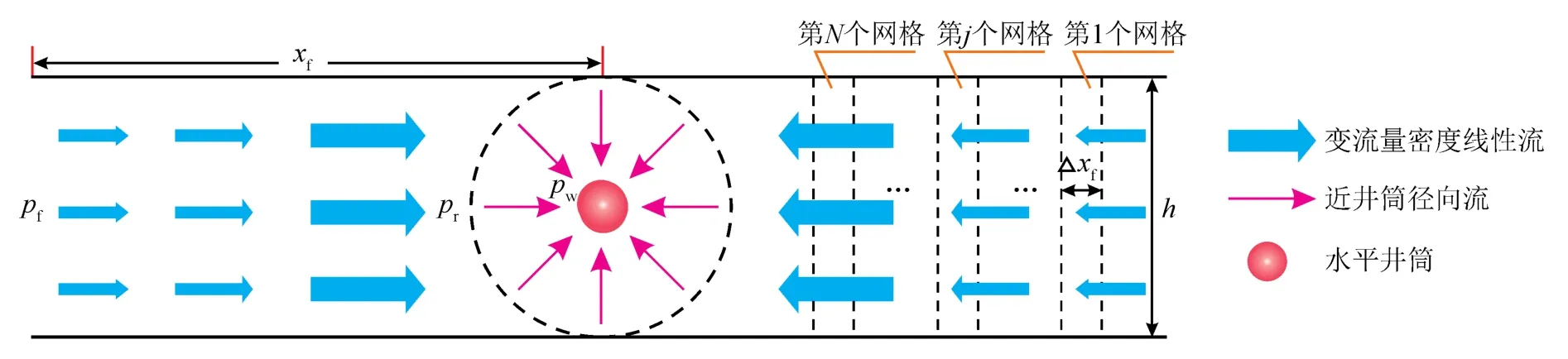
图2 流体在裂缝和井筒中的流动模式示意图
将裂缝内流体的流动简化为一维稳态流动[21],使用流量密度函数εf(x)描述流体沿裂缝的流动。点源函数δ描述井筒的采出,则第n条裂缝内流体流动的无量纲方程为:

式中xD表示无量纲裂缝坐标;xwfD表示无量纲井筒位置坐标;qcD表示无量纲截面流量;LfD表示无量纲裂缝长度;表示长度积分符号;下标n表示第n条裂缝。
无量纲动态导流能力计算式为:
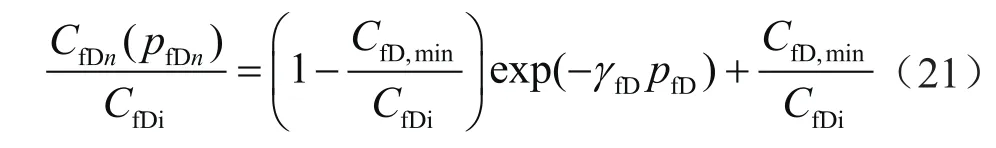
式中CfD,min表示最小无量纲导流能力。
式(20)是典型的非线性微分方程,无法直接求解。笔者采用坐标转换法进行线性化处理,转换式为:
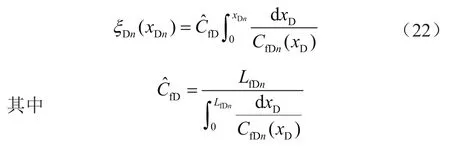
将式(22)代入式(20),再进行偏导数转换,可得新的压力控制方程,即
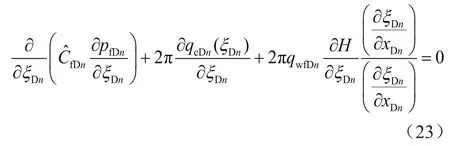
式中H表示Heaviside阶跃函数。
式(23)符合线性微分方程的形式,对该式进行双重积分,同时考虑近井筒附近的聚流效应,可以获得裂缝内的无量纲压力方程,即
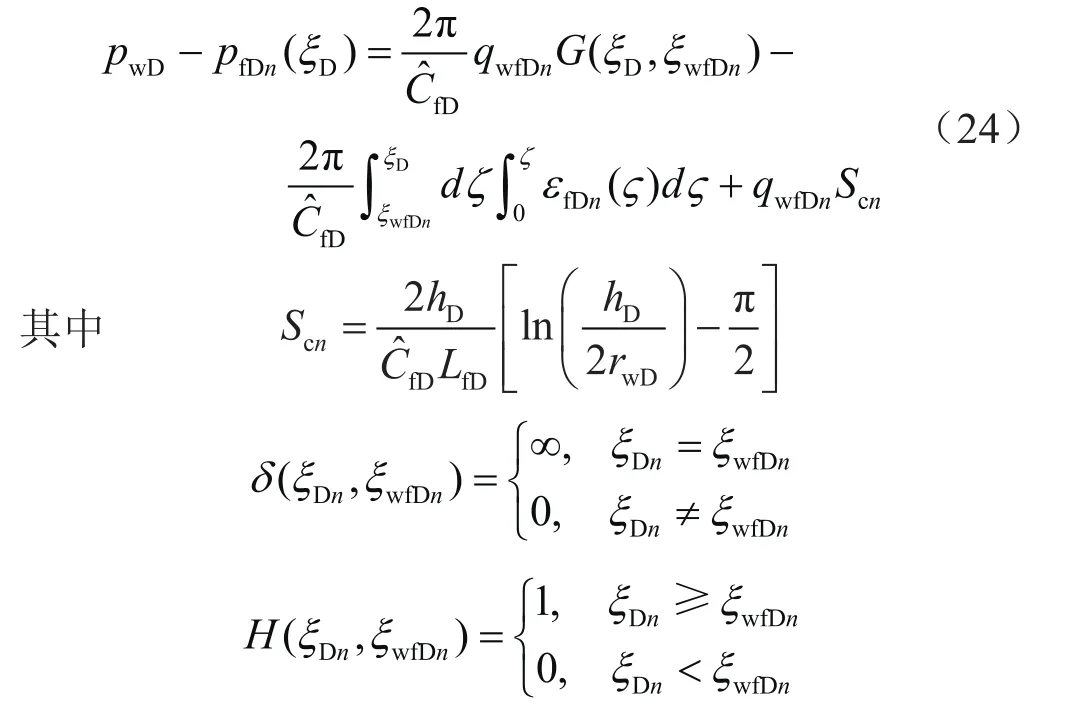
式中pwD表示无量纲井底压力;G表示Heaviside阶跃函数的积分函数;ξwfD表示转换坐标下的无量纲井筒位置坐标;Sc表示裂缝内聚流表皮因子;hD表示无量纲储层厚度;rwD表示无量纲井筒半径。
对式(24)进行离散化处理,认为流体流量在裂缝网格上均匀分布,对应离散形式为:
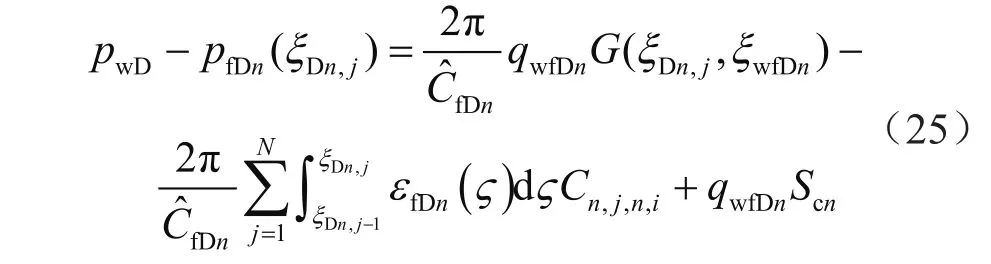
式中C表示裂缝导流影响函数;下标i、j表示裂缝网格序号。
地层边界Γ满足的封闭条件为:
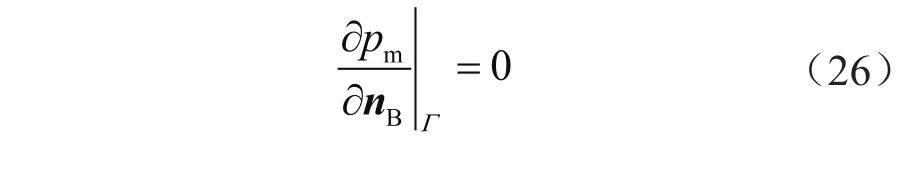
式中pm表示储层压力,Pa;nB表示沿边界的法向量,m。
以每个裂缝网格几何中心为计算点,根据位势叠加原理可以得到第n条裂缝第j个网格内的压力分布,即
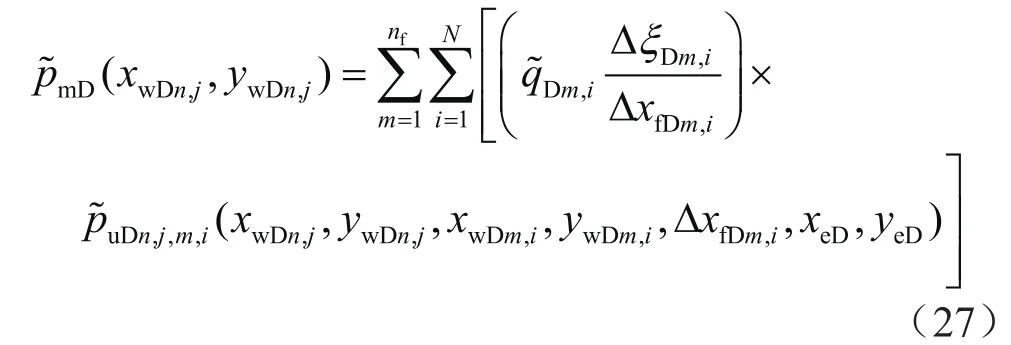
利用Green函数和Newman乘积法[22]计算裂缝微元对应的压力扰动解。在裂缝面上对储层与裂缝系统进行压力与流量的耦合,即
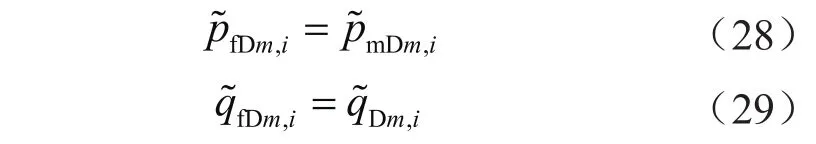
分别将式(25)、(27)代入式(28)、(29),得耦合流动方程组为:
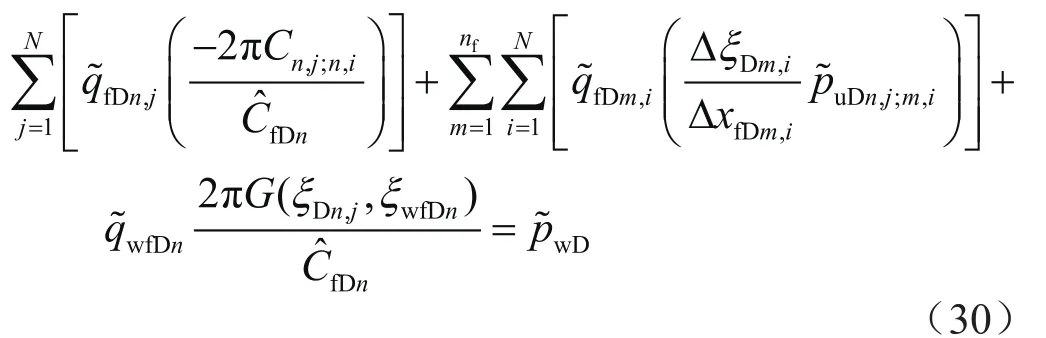
式(30)是关于裂缝网格流量密度、裂缝流量和井底压力的方程组,可写成如下复合矩阵形式,即
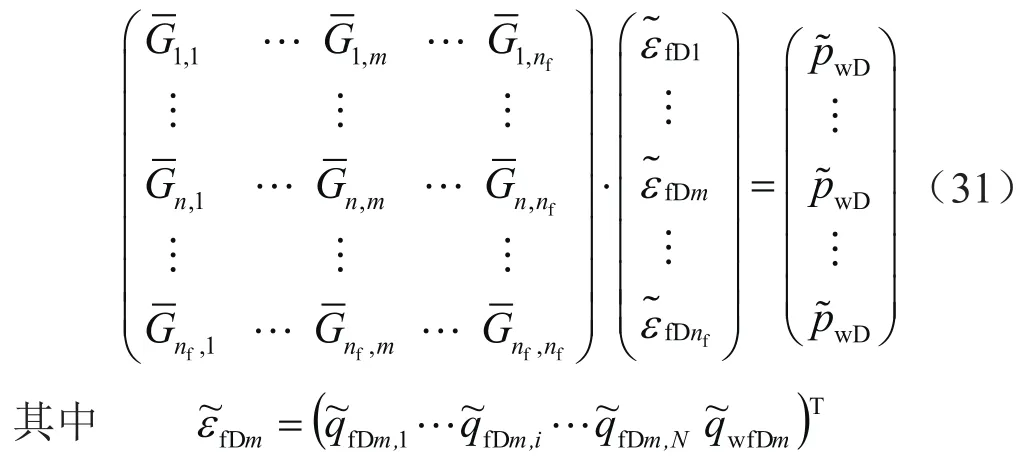
第n条裂缝对第m条裂缝产生的子矩阵为:
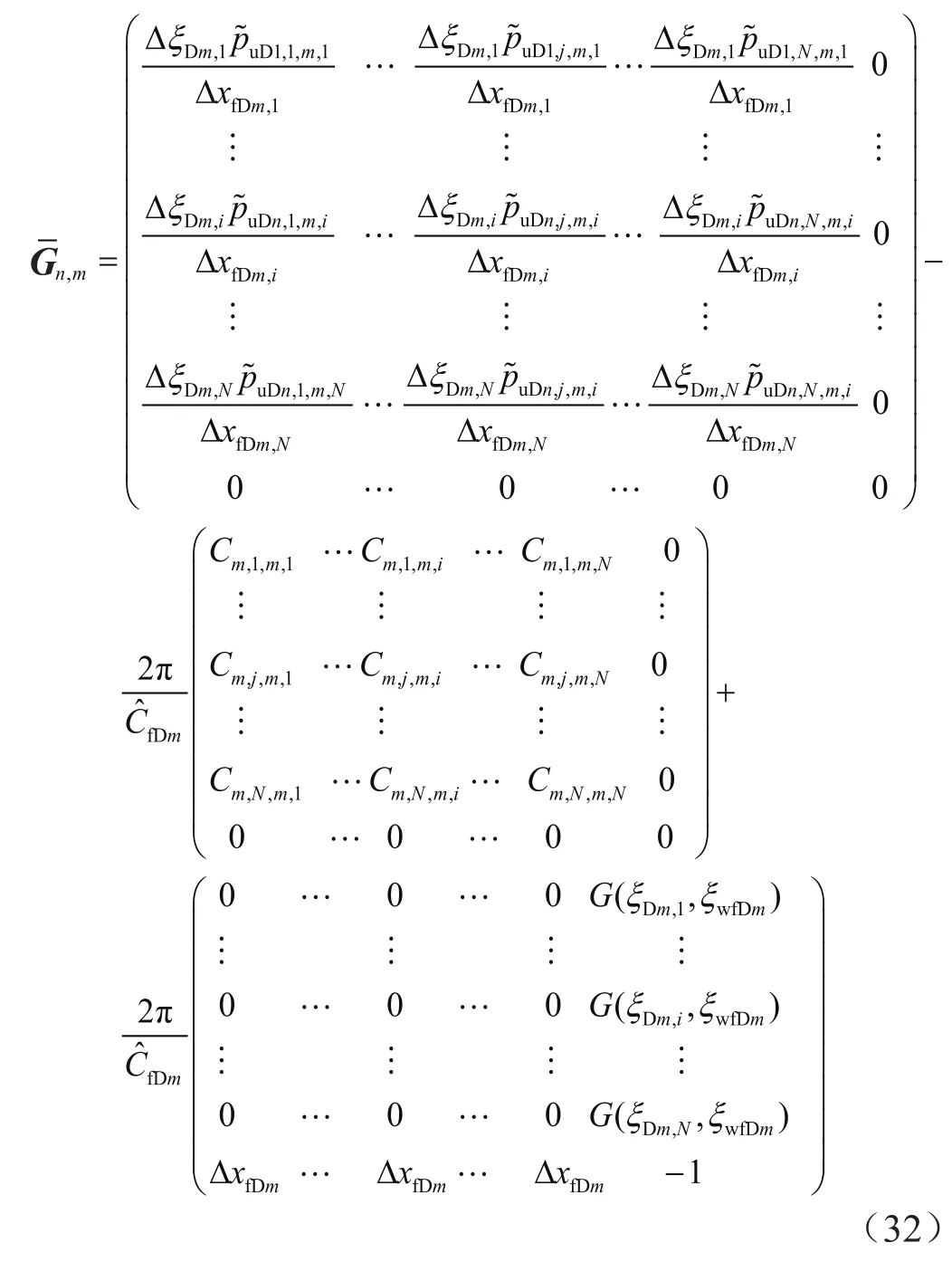
式(32)等号右侧第1个矩阵为地层流动矩阵,只与裂缝网格空间位置有关,第2个矩阵为裂缝内部流动矩阵,第3个矩阵为井筒流出矩阵。
2 模型求解及验证
式(22)表明ξD是裂缝方向上与压力分布相关的函数,若给定第k个时间步的压力分布,则可获得该时间步下沿裂缝方向的导流能力分布。因此,可以由式(31)、(25)分别计算得到第k个时间步沿裂缝的无量纲流量与压力,然后根据式(33),在新坐标系[由式(22)转换得到]下计算第(k+1)个时间步沿裂缝的无量纲压力,结果由所编制的程序通过迭代计算得到。
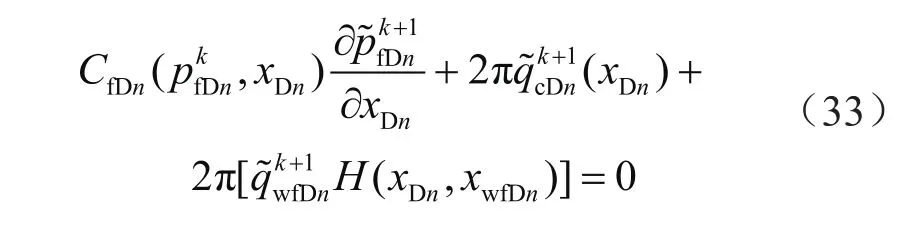
本文所提出的半解析模型的优势在于能够快速模拟封闭地层中变应力敏感系数影响下的压裂井生产动态。将本文模型的计算结果与经典模型的计算结果进行对比,对于有限导流的对称裂缝,采用Cinco-Ley等[21]建立的模型进行计算,对于有限导流的非对称裂缝,采用Berumen等[22]建立的模型进行计算,均不考虑聚流表皮因子的影响,裂缝条数设为1,地层为无限大。如图3所示,本文模型与经典模型的计算结果基本吻合。
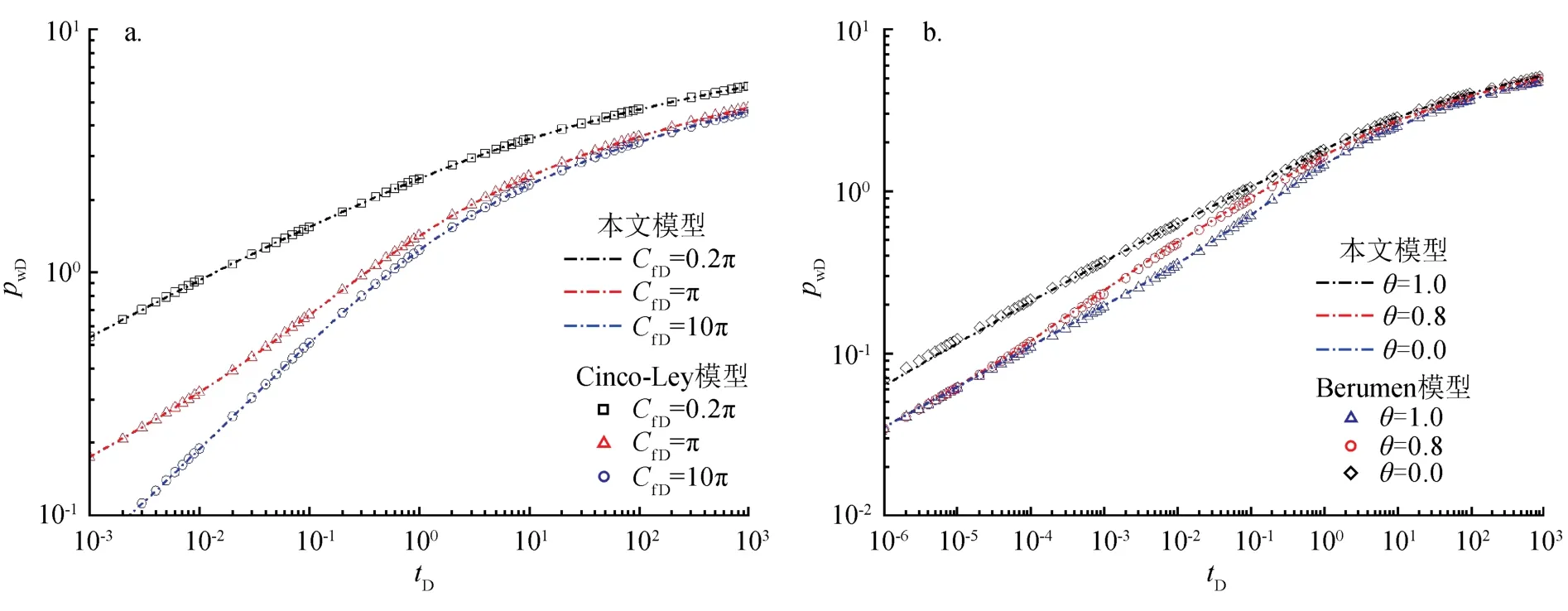
图3 本文模型与经典模型计算结果对比图
对于存在多条裂缝的情况,将本文模型的计算结果与Saphir软件数值模型的计算结果进行对比,设置储层厚度为2.9 m,基质渗透率为0.001 mD,基质孔隙度为10%,裂缝宽度为0.012 7 m,裂缝半长为114.95 m,裂缝孔隙度为35%,原始地层压力为50 MPa,流体黏度为1 mPa·s,综合压缩系数为4.35×10-4MPa-1,裂缝条数为15条,初始无量纲导流能力为10π,最小无量纲导流能力为0.1π,模型长度为4 598 m,宽度为2 299 m,aD、bD选取4种不同的组合,其中组合1(aD=0、bD=0)对应于不存在应力敏感性的裂缝模型,组合3(aD=0、bD=1)对应于常应力敏感系数裂缝模型,组合2(aD=1、bD=1)、4(aD=1、bD=0)对应于变应力敏感系数裂缝模型。通过对比,发现本文模型与Saphir软件数值模型的计算结果基本吻合(图4)。
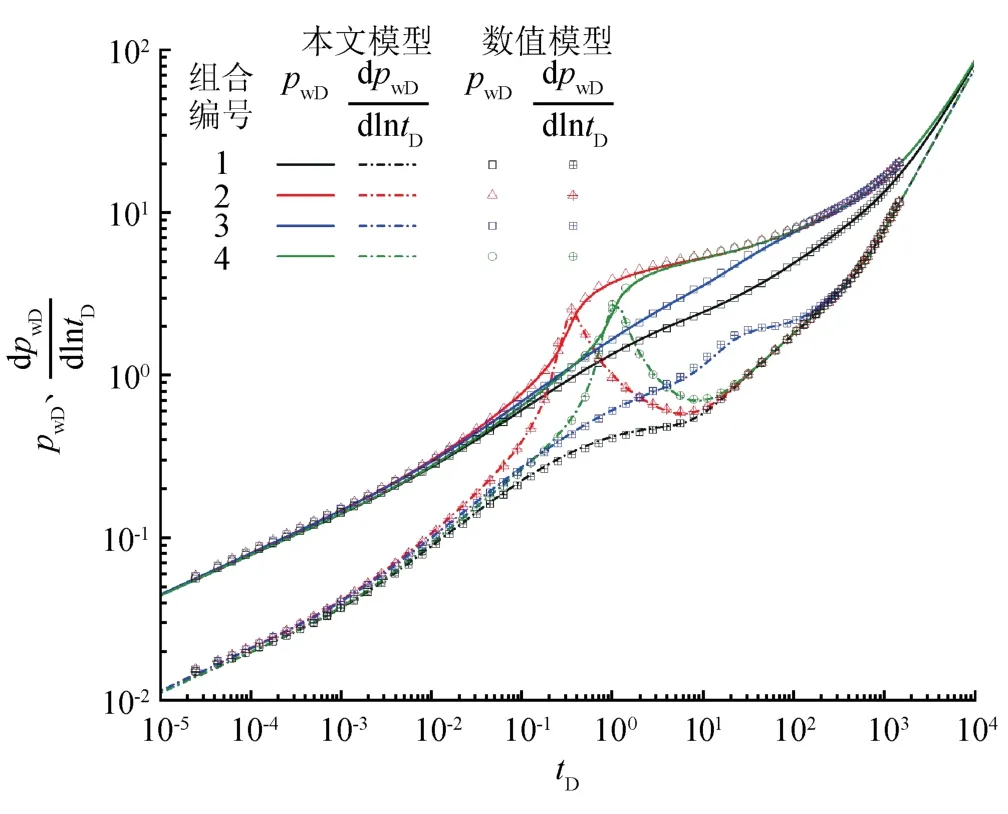
图4 本文模型与Saphir软件数值模型计算结果对比图
3 影响因素分析及实例应用
3.1 影响因素分析
影响压裂水平井生产动态的因素可分为裂缝参数(包括裂缝初始导流能力、长度、条数及空间位置等)和应力敏感性特征参数(包括aD、bD及最小导流能力)。本文建立一种理想模式,即在泄流区域的中心位置均匀部署等长、等导流能力、等应力敏感特征参数的多条裂缝进行影响因素分析。若aD、bD都等于0,对应裂缝则为常导流能力裂缝(简称常导流缝),否则为动态导流能力裂缝(简称动态导流缝)。
对于动态导流缝,随着气井的生产,裂缝发生闭合,裂缝导流能力降低,压力波的传播受到抑制。相同时间内常导流缝压力波的传播速度要快于动态导流缝压力波的传播速度(图5);随时间的延续,裂缝导流能力逐渐降低,且趋近于井点处的裂缝导流能力(图6)。
如图7所示,随着tD增加,气井的无量纲产气量qwD(由前述qwfD求和得到)不断递减;对于动态导流缝,aD、bD的不同组合决定了qwD的下降幅度不同;应力敏感系数较小(aD=1、bD=1)时,qwD曲线趋近于常导流缝(CfD=100π)对应的qwD曲线,应力敏感系数较大(aD=1、bD=10)时,qwD曲线趋近于常导流缝(CfD=0.1π)对应的qwD曲线。
如图8所示,在气井的整个生产周期内,aD=1、bD=1组合下,动态导流缝的CfD都维持在较高水平(介于42.780~314.000),与常导流裂缝(CfD=100π)影响下气井的无量纲累计产气量(GpD)曲线基本重合,这是由于高导流能力(CfD>300)与中导流能力(30<CfD<300)裂缝对气井累计产气量的贡献接近;aD=1、bD=10与aD=10、bD=1组合下,动态导流缝的导流能力较低,且最后趋近于0.315,相应GpD曲线与常导流裂缝(CfD=0.1π)影响下的GpD曲线接近。
另外,裂缝参数(裂缝条数、缝长、缝宽等)也会对气井生产动态产生影响,尤其增加裂缝条数、缝长能够有效提高气井累计产气量的增长幅度,因此,合理设计裂缝参数以指导页岩气水平井的压裂实践意义重大。
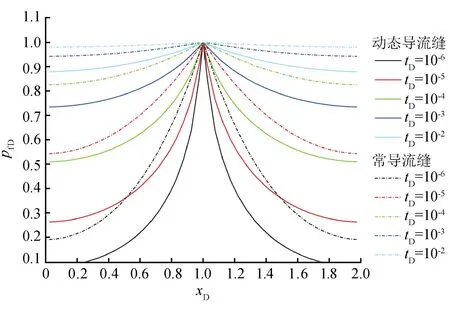
图5 裂缝应力敏感性影响下沿裂缝pfD分布图
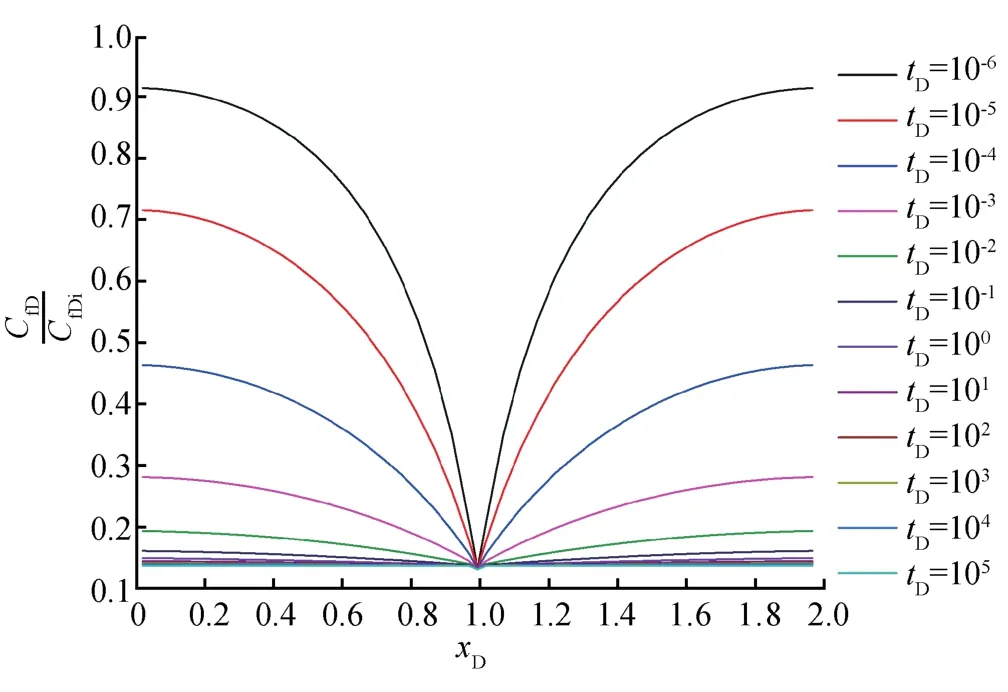
图6 裂缝应力敏感性影响下沿裂缝分布图
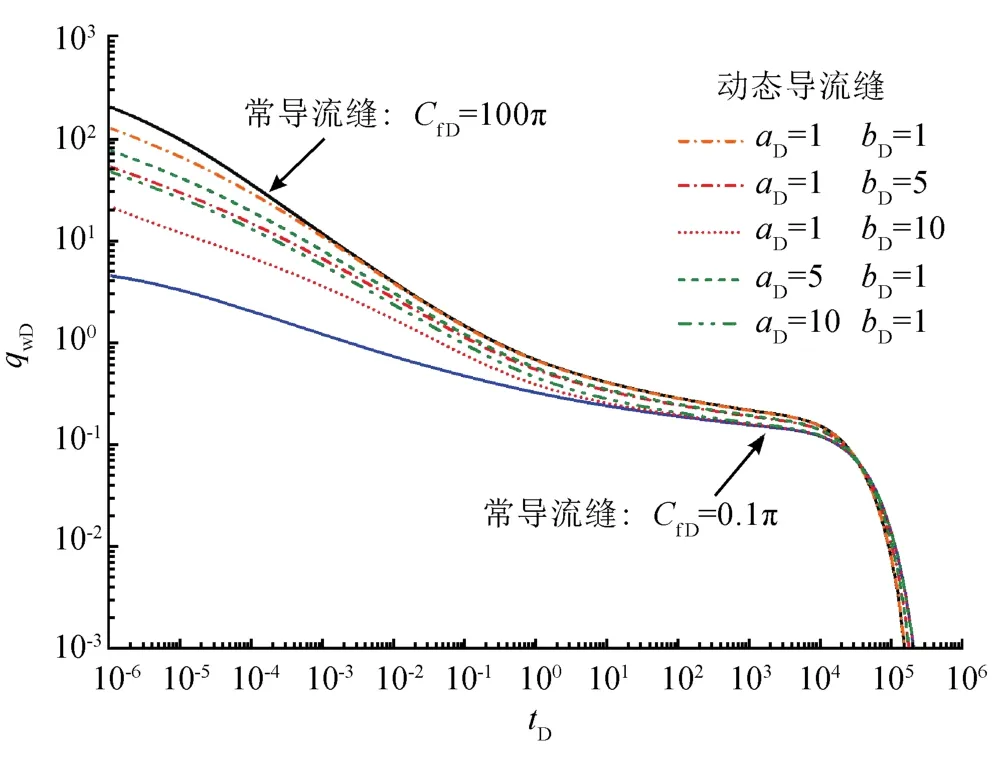
图7 考虑裂缝应力敏感性影响的气井qwD曲线图
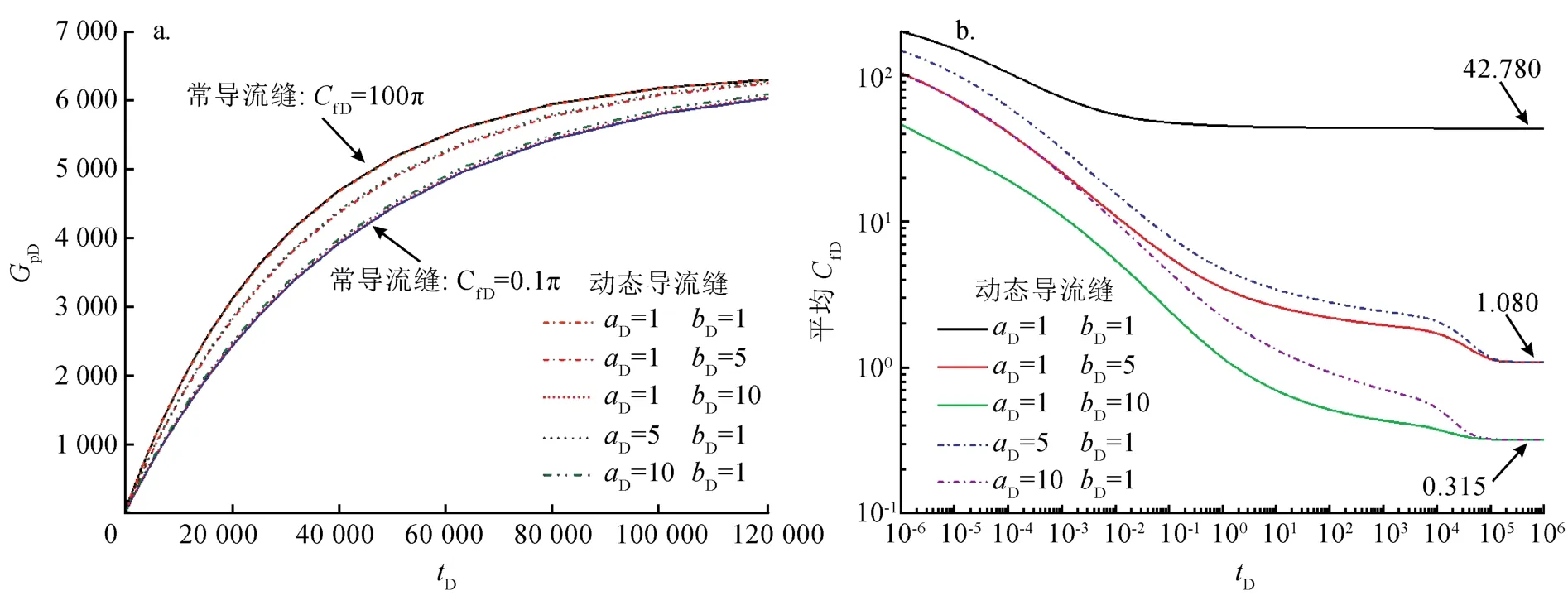
图8 考虑裂缝应力敏感性影响的气井GpD及平均CfD曲线图
3.2 控压增效潜力分析
气井生产采取控压方式时,对于存在动态导流缝的情况,气井的无量纲压力随着时间增加逐渐偏离存在常导流裂缝情况下气井的无量纲压力;而气井生产采取放压方式时,自开井伊始动态导流缝的导流能力即发生大幅度衰减,产量即偏离常导流缝存在时的气井产量,且定压时间越早,偏离程度越大。当无量纲井底压力较小时,累计产气量也较小,且无论裂缝导流能力为常量还是变量,对气井累计产气量的影响基本一致。(图9)
因此,制订合理的井底压力,可以控制裂缝的闭合,缓解产量降低的幅度,进而提高气井的累计产气量。本文采用式(31)来表征控压生产中井底压力的变化,当平均衰减寿命取无穷小时,即相当于气井一开井则进入定压阶段。
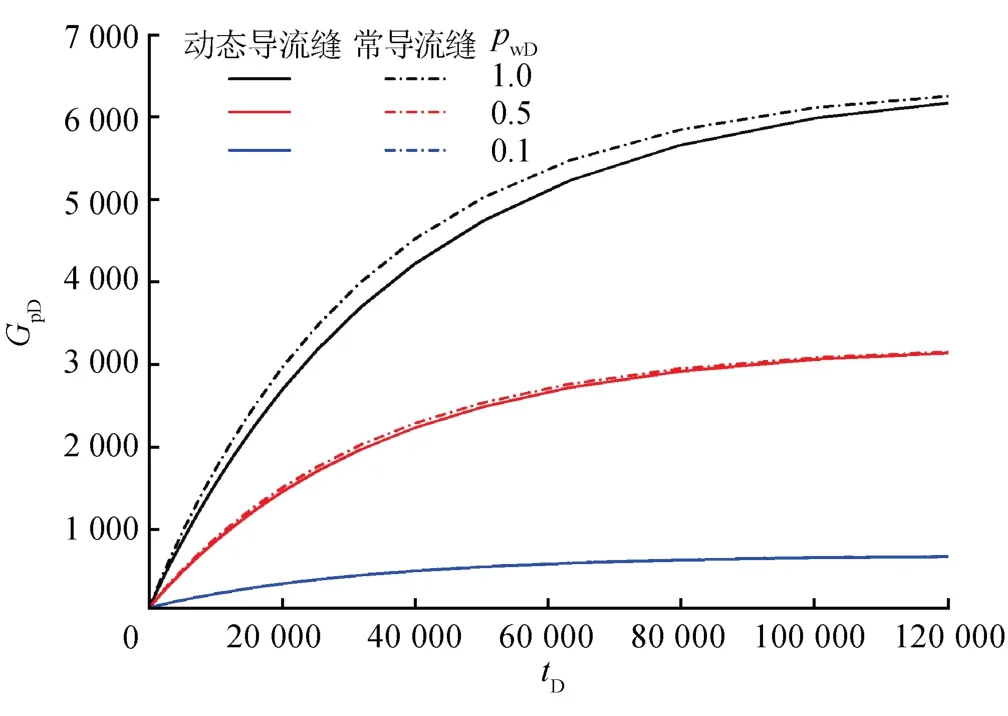
图9 不同pwD下气井GpD曲线图
井底压力与平均衰减寿命的关系式为:
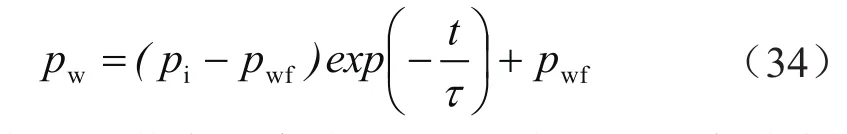
式中pwf表示定井底压力值,Pa;τ表示平均衰减寿命,s。
由式(7)定义应力敏感系数,模拟不同τD下气井的累计产气量,结果显示与放压方式相比,控压方式下的累计产气量虽在生产早期低于放压方式下的累计产气量,但最终的累计产气量更高,该结果也与采用流固耦合模型模拟的结果[4,15,17]趋势一致(图10);同时,使用变应力敏感系数模型计算的累计产气量要低于常应力敏感系数模型计算的结果,这与Mirani等[16]使用流固耦合模型计算的结果也一致,进一步验证了所建立模型的正确性。
如图11所示,在放压方式下,由于裂缝闭合严重,导致裂缝导流能力迅速递减至最小值,而气井一开井产气量即为最高,随后逐渐递减,无稳产期;在控压生产方式下,井底压差逐渐增加至最高值,延缓了裂缝导流能力衰减的速度,气井产气量呈现为逐渐增加至最高值后,再逐渐递减的变化趋势;在某个时间点后控压方式下的气井产气量将超过放压方式下气井的产气量,若控压制度制订合理,气井的生产将出现明显的稳产期。
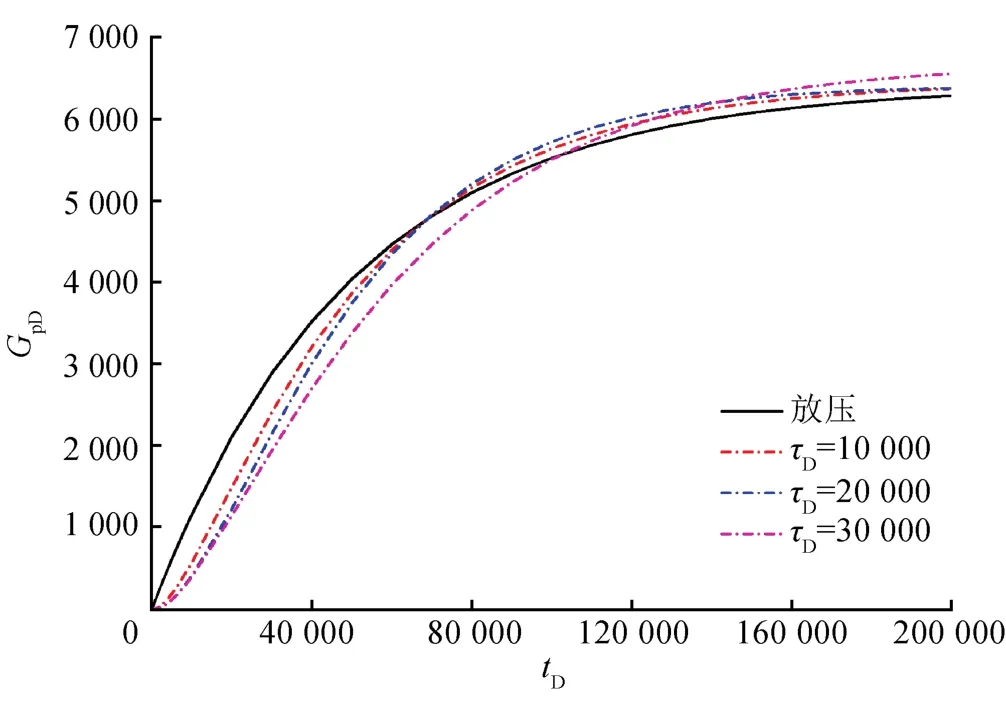
图10 不同τD下单井GpD曲线图(aD=1、bD=1)
3.3 实例应用
压裂水平井的开发效果取决于地质条件、工程条件和生产制度等因素。此次选取某建产区地质参数和工程参数相近、生产制度不同的两口井进行分析,其中HD井采用短期控压方式生产,MD井采用长期控压方式生产。在地质方面,龙马溪组的优质页岩段为龙一1亚段,其中又以龙和龙小层为最优,是水平井钻进的最优靶位,如表1所示,HD井钻遇龙和龙小层的长度合计为717.7 m,而MD井仅钻遇龙小层513.6 m;在工程方面,HD井的压裂段长度和压裂段数虽低于MD井,但其压裂加砂量是MD井加砂量的1.5倍(表2)。总体判断,若无其他因素的影响,HD井的开发效果应优于MD井。
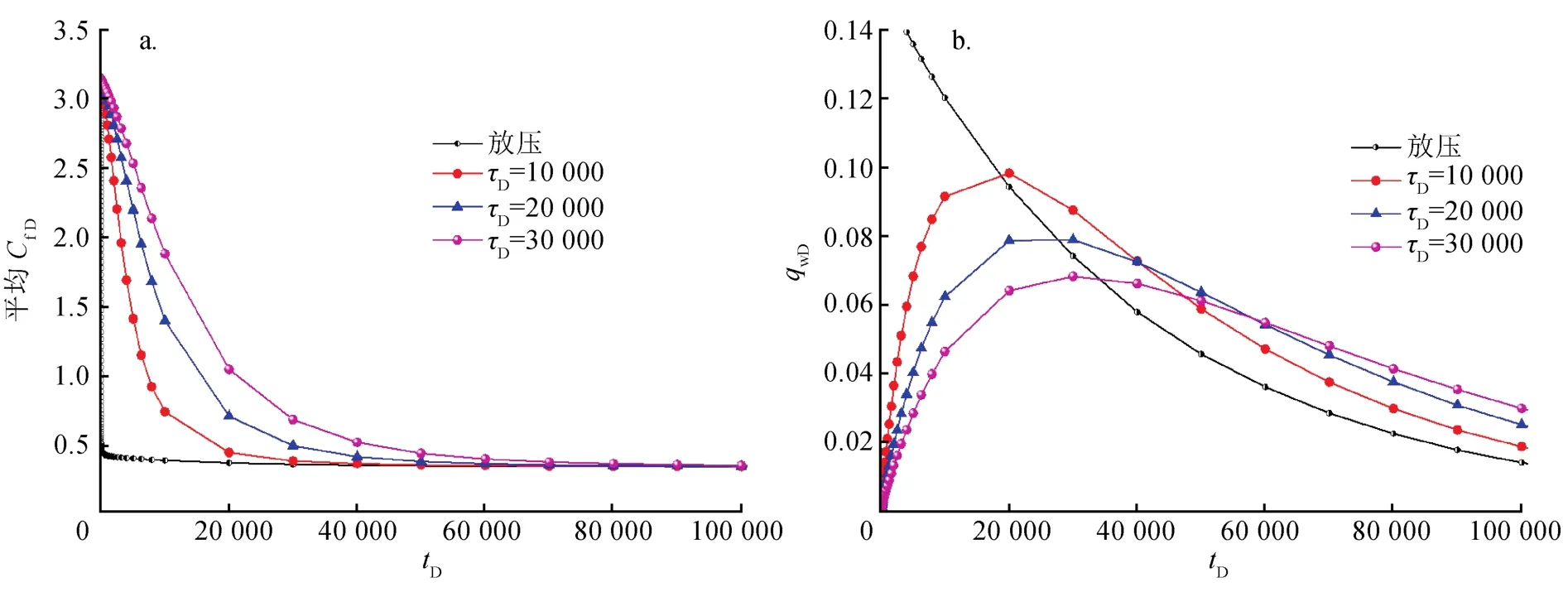
图11 放压、控压方式下平均CfD、qwD曲线图
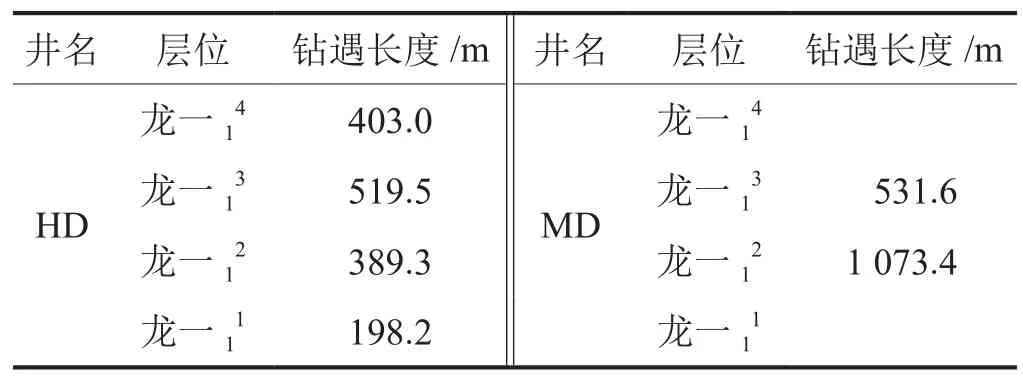
表1 水平井页岩层位钻遇情况统计表
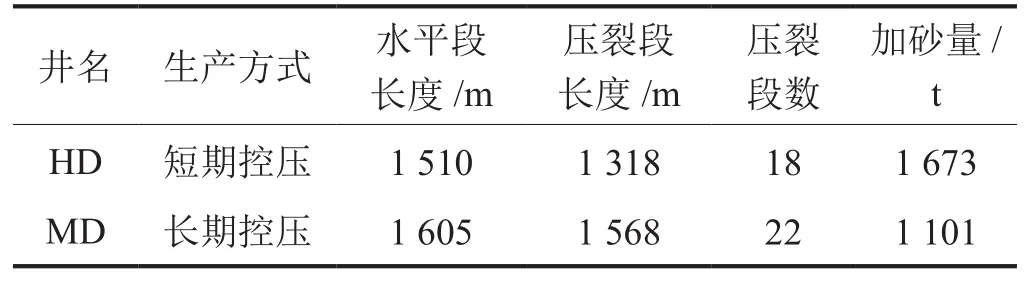
表2 水平井工程参数对比表
但从气井的实际生产动态来看,HD井前3个月的压降速率为0.278 MPa/d,MD井仅为0.13 MPa/d,但MD井前3个月单位压降采气量为64.7×104m3/MPa,远高于HD井的37.8×104m3/MPa,前者是后者的1.7倍;从目前生产情况来看,HD井的日产气量已低于MD井(图12)。造成此种差异的一个重要原因即在于HD井采用短期控压制度进行生产,而MD井采用长期控压制度进行生产。
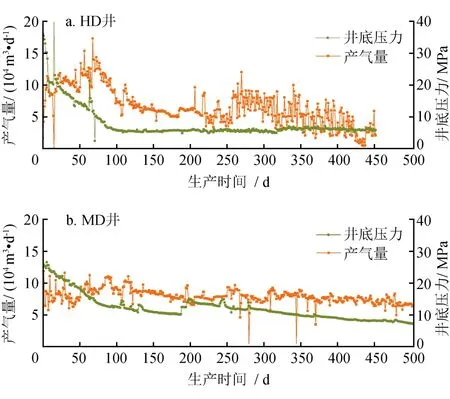
图12 HD井与MD井采气曲线图
通过比较单井EUR更能体现出生产制度差异带来的影响。使用Laplace正演算法将实时空域上井底压力转换为Laplace空间值[23],代入本文模型,对气井产气量进行拟合,获取裂缝动态参数,在此基础上进行产量预测。如图13所示,生产时间在4年以内HD井累计产气量要高于MD井,而5年以后长期控压生产的优势逐渐显现,20年末MD井的累计产气量为0.805×108m3,而HD井的累计产气量为0.636×108m3,前者是后者的1.27倍。可以看出,合理的控压生产制度可以使气井累计产气量增加25%以上。
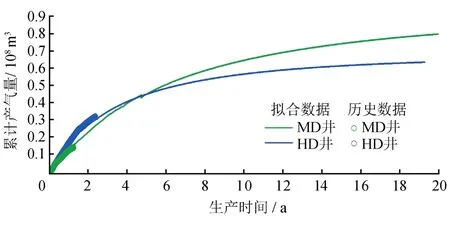
图13 HD井与MD井累计产气量拟合及预测曲线图
4 结论
1)所建立的模型与经典模型、Saphir软件数值模型计算的结果基本吻合;
2)应力敏感性的存在使得裂缝导流能力随着气井生产而递减,从而导致气井累计产气量减低,且应力敏感性越强,累计产气量减低的幅度越大;
3)与放压方式相比,采用控压方式生产的页岩气压裂水平井的初期产气量及累计产气量虽偏低,但最终累计产气量却更高,可以看出页岩气压裂水平井采取长期控压生产的方式更具合理性。
