声速分布对浅海低频声场空间相关的影响研究
2019-09-02朱军祝捍皓屈科郑广学胡佳臣
朱军 ,祝捍皓 ,屈科 ,郑广学 ,胡佳臣
声速分布对浅海低频声场空间相关的影响研究
朱军1,祝捍皓2,屈科3,郑广学2,胡佳臣2
(1. 浙江海洋大学船舶与机电工程学院,浙江舟山 316022;2. 浙江海洋大学海洋科学与技术学院,浙江舟山 316022;3. 广东海洋大学电子与信息工程学院,广东湛江 524088)
针对浅海低频环境下水中声速分布对声场空间相关性的影响问题,利用基于抛物方程方法的RAM程序,仿真分析了声场空间相关特性在浅海不同声速梯度、不同阵元间隔下的变化规律。研究结果表明:在浅海低频环境下,正声速梯度值越大,垂直相关系数衰减越慢,水平纵向相关系数则相反;随着正声速梯度值的增大,垂直相关长度和水平纵向相关长度均呈现剧烈波动。负声速梯度值越大,垂直相关系数衰减越快,水平纵向相关系数则相反;随着负声速梯度值的增大,两类空间相关长度均缓慢波动。
浅海声场;抛物方程法;声速分布;空间相关
0 引言
在当前水声工程中,就标量水听器的应用而言,使用标量水听器阵列比单个水听器有明显的优势,其中一个重要原因是水听器阵列中各个阵元接收的相关信号,可获得单个水听器不具备的阵增益性能,以此得到更佳的应用效果。而阵列中阵元间的空间相关系数则是度量阵增益的一个重要指标[1]。
因此,充分了解声场的空间相关性及其变化规律,对声呐基阵的合理设计、性能预报具有重要的理论指导意义。此外,随着水声工程研究的不断发展,基于声场空间相关性的海底声参数反演、海洋噪声场等研究成果不断涌现,也促进了研究者对水下声场空间相关特性物理机制深入探索。
考虑我国大陆架周围海域大部分属于浅海范畴,因此,国内对浅海低频声场空间相关性[2-3]的研究尤为关注,并已涌现了大量成果,如:苏晓星等[4]指出,在一定条件下声源深度是浅海低频水平纵向相关的一个敏感参数;宫在晓等[5]、邵炫等[6]证明了浅海低频纵向相关的起伏变化,是由各号简正波之间干涉的空间变化引起的,且随着接收距离的增加,对声场有贡献的有效简正波号数减少,声场的空间纵向相关半径趋于增大;赵梅等[7-8]分析了不同倾斜海底对声场空间相关系数的影响,同时还提出了利用声场垂直相关性来反演浅海倾斜海底声参数的方法。上述研究极大丰富了浅海低频声场相关性的研究内容,但其中声速剖面变化对浅海低频声场相关性影响的研究[9-10]内容则相对较少。
在浅海环境下,受温度、盐度等参数的影响,声速剖面复杂多变,将对声传播特性产生重要影响,进而导致声场相关性的变化。为此,本文在一类理想水平分层浅海环境模型下,利用基于抛物方程方法(Parabolic Equation, PE)的RAM程序进行数值模拟,分析了声场空间相关特性在不同声速分布下对垂直、水平纵向相关系数的影响规律,以期为声场空间相关性在浅海低频环境中的应用提供更加完备的理论基础。
1 空间相关系数定义
空间相关系数与空间相关长度是研究声场空间相关性的两个关键参数。声场空间相关系数是指在不同深度(或者水平)距离位置下,接收阵元和参考阵元接收到同一声源的信号波形之间的空间相关函数与信号能量的比值,表征空间上具有垂直间隔或水平偏移的两个接收点上声场的相似程度,其计算式为
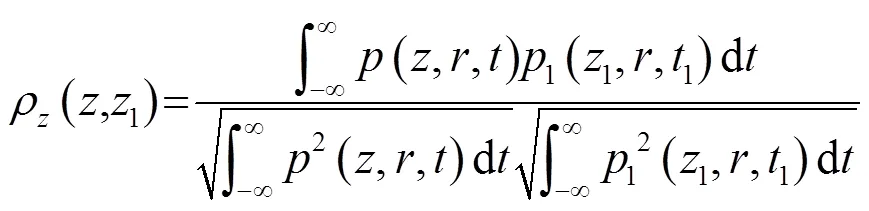
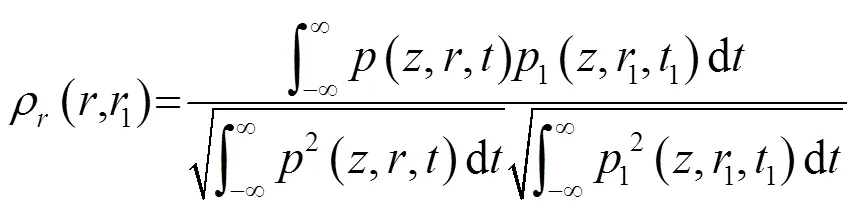
声场空间相关长度的定义是当声场空间相关系数第一次下降到0.707时,对应参考阵元与接收阵元的间距[11-12]。
由傅里叶(Fourier)变换的性质,可得到式(1)、(2)离散化后的空间相关系数的频域计算公式:


考虑现有声场仿真程序多是在频率域上进行求解,在下文的研究中将应用式(3)、(4)并结合抛物方程方法计算空间相关系数与空间相关长度。

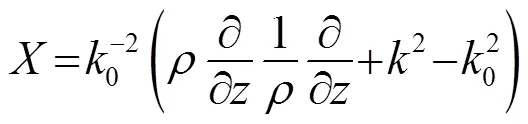
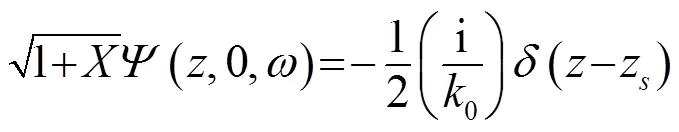
2 仿真分析

利用基于抛物方程方法的RAM程序[14]进行数值模拟,仿真分析了频率计算范围在100~200 Hz时,不同声速分布下声场空间相关系数与相关长度随着仿真参数变化的规律。
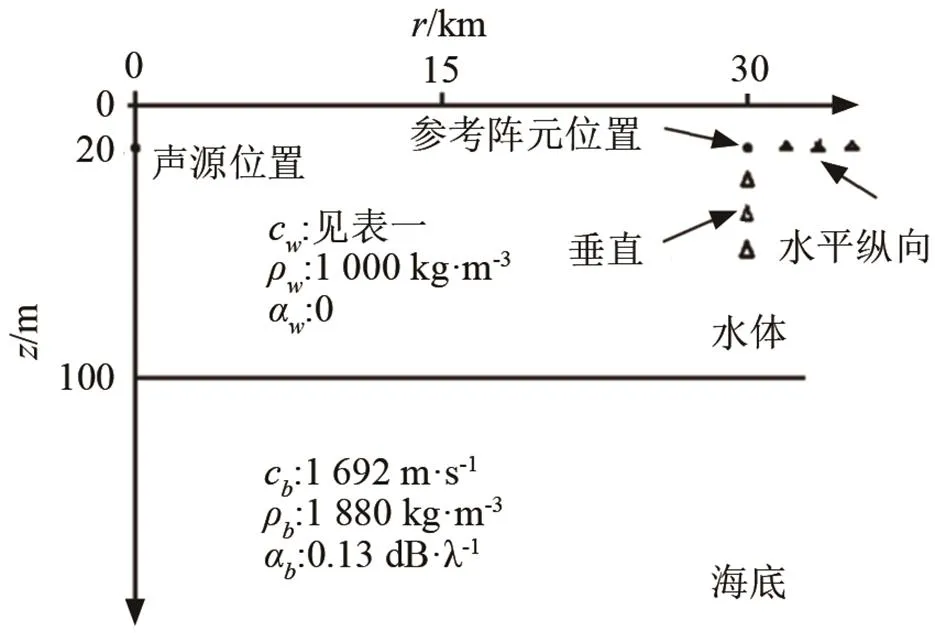
图1 数值仿真采用的浅海模型
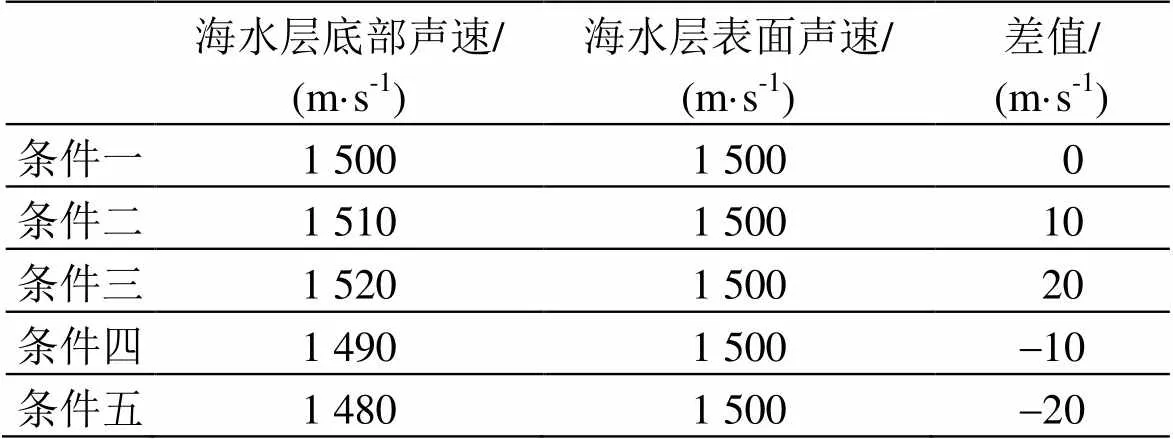
表1 数值仿真中的水体声速参数
注:表1中差值为海水层底部声速与海水层表面声速之差
2.1 声场垂直相关分析
2.1.1 不同声速分布下声场垂直相关系数分析
图2给出了在图1所示的仿真环境下,声速分布分别为表1中的仿真条件等声速、正声速梯度、负声速梯度时,声场的垂直相关系数随着接收阵元与参考阵元间垂直距离变化的曲线。

图2 不同声速梯度下垂直相关系数的变化曲线
观察图2可以发现,在图1所示的浅海环境与表1中不同声速梯度的仿真条件下,垂直相关系数衰减的速度由快至慢分别为负声速梯度、等声速和正声速梯度。在正声速梯度的浅海环境下,声线传播时会向海面偏转,使得在水体下层的声线分布相对分散,声场的干涉结构简单,使得对应接收点接收到声压的相位变化较等声速梯度环境下弱,在垂直方向上的相关系数衰减得较慢。而对于在负声速梯度的浅海环境下,声线传播时会向海底偏转,使得在水体下层的声线分布相对集中,声场的干涉结构复杂,在对应接收点接收到声压的相位变化相较于等声速梯度环境下更复杂,在垂直方向上的相关系数衰减得较强。
在得出不同声速梯度下,垂直相关系数随着参考阵元与接收阵元间垂直距离变化以及衰减的规律后,本文进一步讨论、分析了在不同的正声速梯度、负声速梯度下垂直相关系数的变化规律。图3、图4分别给出了图1所示的仿真环境下,声速分布分别为表1中的仿真条件一(等声速)、二、三(不同正声速梯度)下和仿真条件一(等声速)、四、五(不同负声速梯度)下,声场的垂直相关系数随接收阵元与参考阵元之间垂直距离变化的曲线。
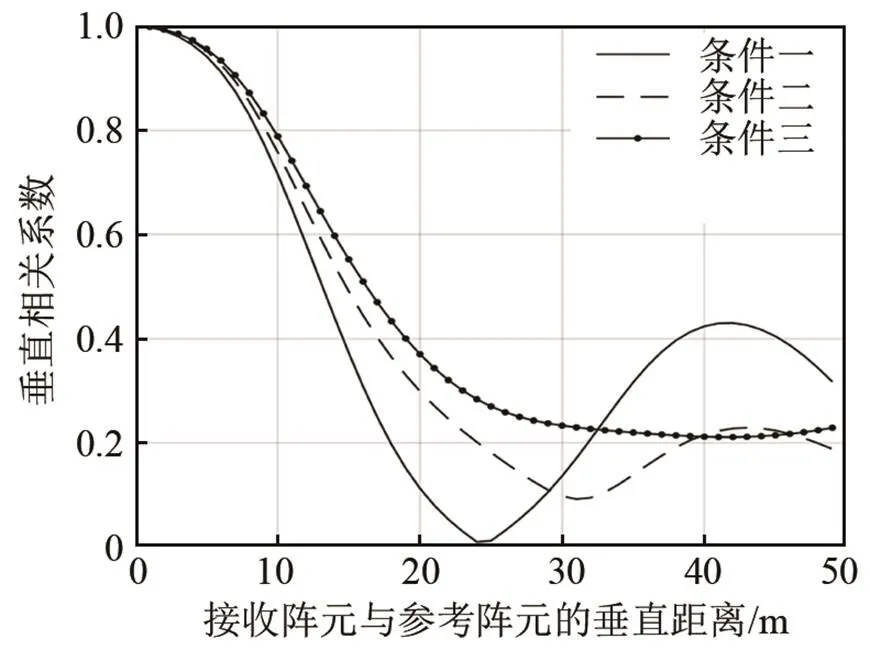
图3 不同正声速梯度下垂直相关系数的变化曲线
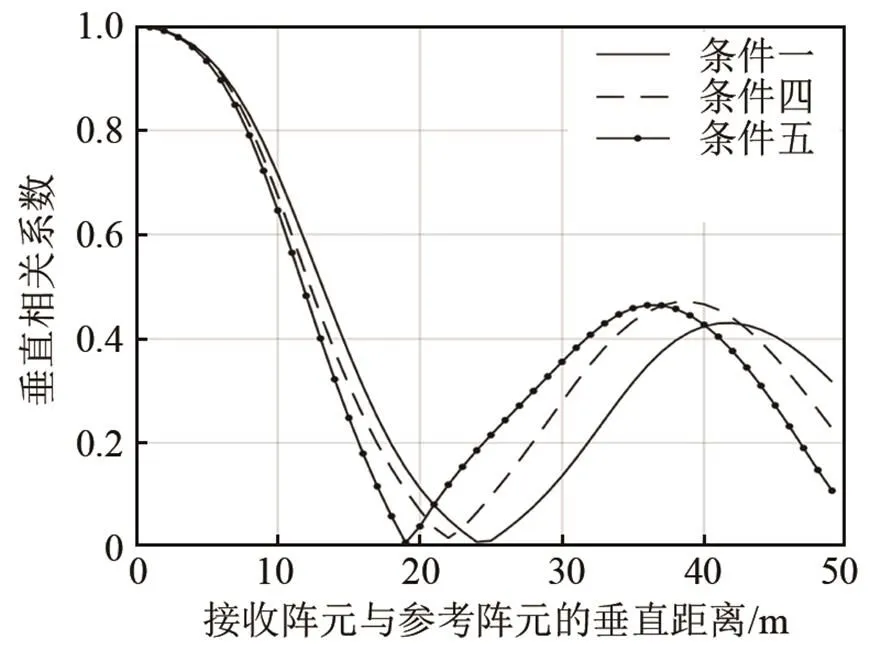
图4 不同负声速梯度下垂直相关系数的变化曲线
对比图3、4可以发现,在图1的仿真环境下,正声速梯度值越大,水体下层的声线分布越分散,声场的干涉结构越简单,使得垂直相关系数衰减越慢,垂直相关系数随阵元间隔的起伏周期越小;当声速分布在不同的负声速梯度时,负声速梯度值越大,在水体下层的声线分布越集中,声场的干涉结构越复杂,使得垂直相关系数衰减越快,垂直相关系数的变化曲线呈现相对一致的起伏变化规律。
2.1.2 不同声速分布下声场垂直相关长度分析
在讨论不同声速分布下声场垂直相关系数变化规律的基础上,图5、6讨论了在图1所示的仿真环境下,不同声速分布下声场垂直相关长度的变化规律。图5给出了海水层表面声速在1 500 m·s-1时,随着海水层底部声速变化(1 480~1 520 m·s-1),垂直相关长度的变化曲线图。图6给出了海水层表面声速在1 520 m·s-1时,随着海水层底部声速变化(1 500~1 540 m·s-1),垂直相关长度的变化关系。
图5、6中的横坐标代表海水层底部声速与海水层表面声速的差值。当横坐标数值为正数时,声速分布为正声速梯度分布,差值越大,说明正声速梯度越大;当横坐标数值为负数时,则声速分布为负声速梯度分布,差值越大,说明负声速梯度越大;当横坐标数值为0时,则声速分布为等声速分布。后面讨论分析水平纵向相关长度时亦是如此。

图5 海水层表面声速在1 500 m·s-1,在不同海水层底部声速下垂直相关长度的变化关系
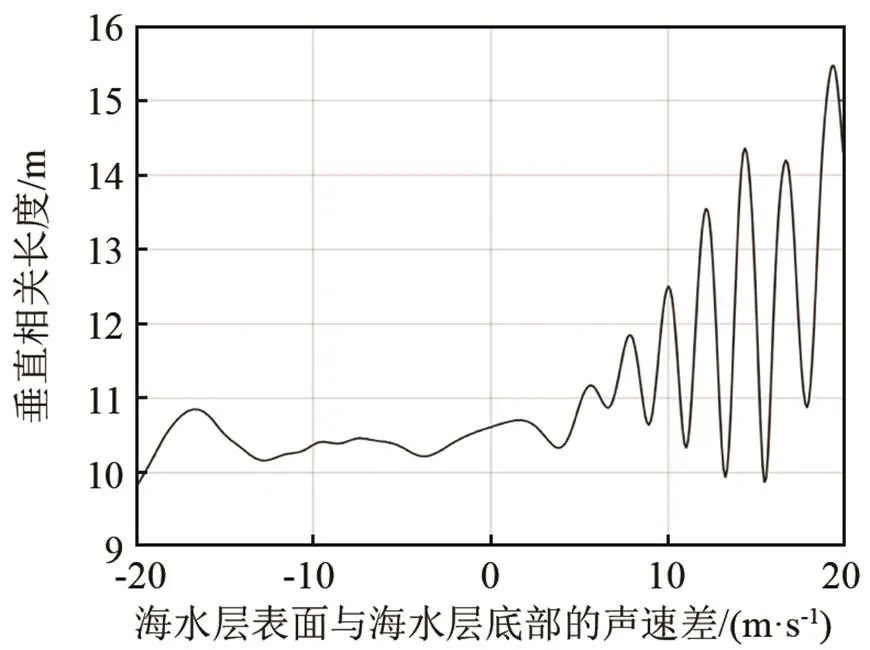
图6 海水层表面声速在1 520 m·s-1,在不同海水层底部声速下垂直相关长度的变化关系
通过图5、6的对比可以发现,当声速分布为正声速梯度时,随着正声速梯度值的增大,垂直相关长度呈现稳定的起伏增加,同时伴有强烈的起伏性;当声速分布处于负声速梯度时,随着负声速梯度值的增大,垂直相关长度逐渐减小,同时有一定的起伏,但起伏现象比较缓慢。当海水层表面声速在1 500 m·s-1时,正声速梯度的情况下,随着海水层底部声速的增大,垂直相关长度从10.2 m起伏上升到14.2 m;在负声速梯度下,随着海水层底部声速的减小,垂直相关长度从10.2 m起伏下降至9.2 m。而当海水层表面声速在1 520 m·s-1时,正声速梯度的情况下,随着海底声速的增大,垂直相关长度从10.6 m起伏上升到14.6 m;在负声速梯度下,随着海水层底部声速的减小,垂直相关长度从10.6 m起伏下降至10.1 m。可见当海水层表面声速较高时,垂直相关系数的变化范围也会有所抬高。
2.2 水平纵向相关分析
2.2.1 不同声速分布下的水平纵向相关系数分析
在2.1节讨论浅海声速分布对声场垂直相关特性影响的基础上,本节分析声场水平纵向相关系数在不同声速分布下的变化规律。图7给出了在图1的仿真环境下,声速分布分别为表1中的等声速、正声速梯度、负声速梯度时,声场的水平纵向相关系数随着接收阵元与参考阵元间水平纵向距离变化的曲线。
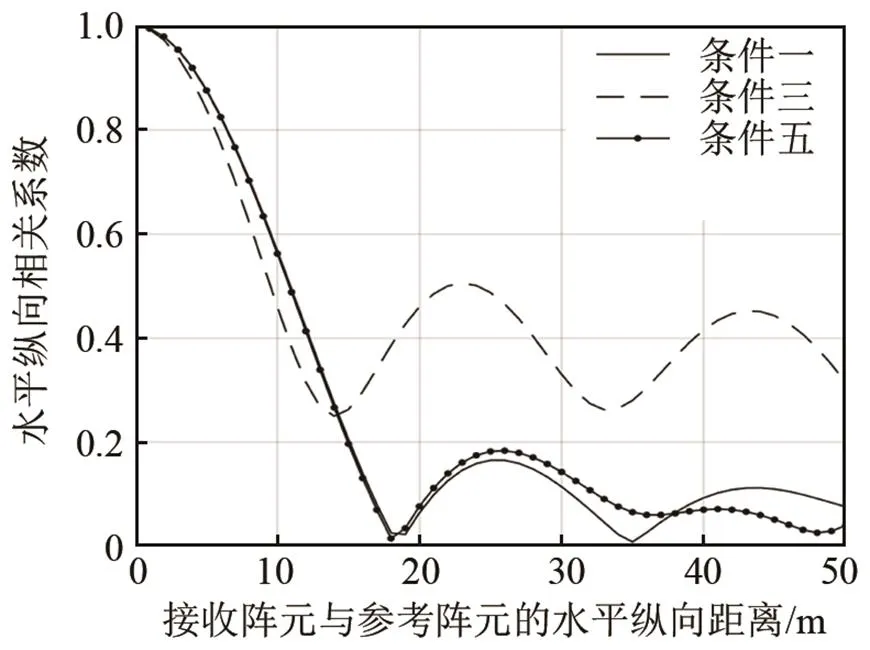
图7 不同声速梯度下水平纵向相关系数的变化曲线
观察图7可以发现,在图1所示的仿真环境与表1中不同声速梯度的仿真条件下,水平纵向相关系数的衰减速度由快至慢分别为正声速梯度、等声速/负声速梯度。在正声速梯度的浅海环境下,声线传播时会向海面偏转,使得在水体上层海表面处的声线分布相对集中,声场的干涉结构复杂。这导致对应接收点接收到声压的相位变化较等声速梯度环境下快,在垂直方向上的相关系数衰减得较快。同时,在一定参考阵元与接收阵元水平纵向距离内,水平纵向相关系数会保持一个较高的波动值。而在负声速梯度的浅海环境下,声线传播时会向海底偏转,使得在水体上层海表面处的声线分布相对分散,但对声场的干涉结构仅有微弱的影响,在对应接收点接收到声压的相位变化与在等声速梯度环境下相似,在水平纵向方向上的相关系数衰减较弱。在得出不同声速梯度下,水平纵向相关系数随参考阵元与接收阵元间水平纵向距离变化以及衰减的规律后,本文将进一步分析在不同正声速梯度、负声速梯度下水平纵向相关系数的变化规律。图8、9分别给出了在图1环境下,声速分布分别为表1仿真条件一(等声速)、二、三(不同的正声速梯度)下和声速分布为表1仿真条件一(等声速)、四、五(不同的负声速梯度)下时,声场的水平纵向相关系数随着接收阵元与参考阵元间水平纵向距离变化的曲线。
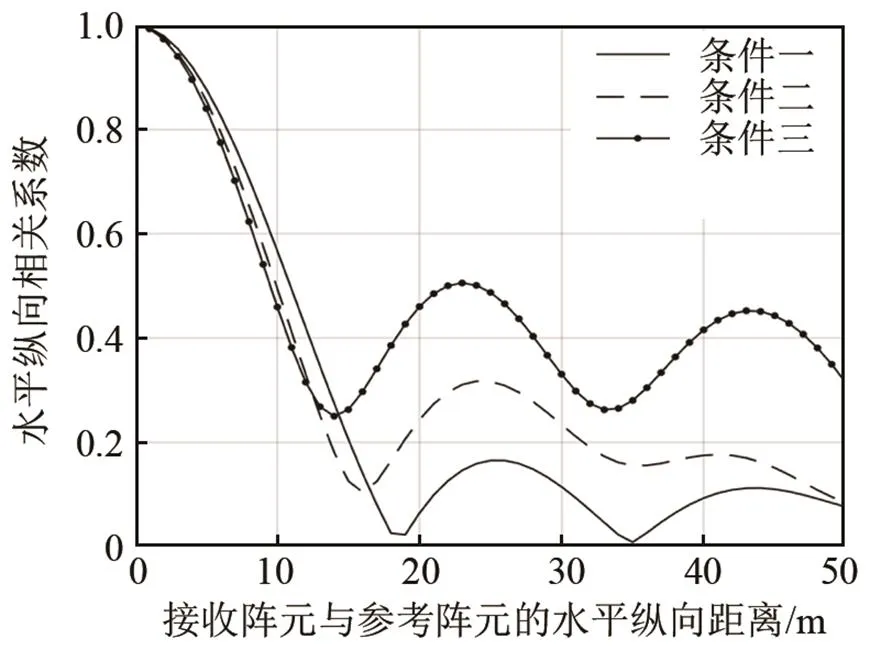
图8 不同正声速梯度下水平纵向相关系数的变化曲线

图9 不同负声速梯度下水平纵向相关系数的变化曲线
通过图8、9的对比可以发现,浅海声速分布在不同的正声速梯度变化下,正声速梯度值越大,在海水层上层处的声线分布越复杂,声场的干涉结构越强,使得水平纵向相关系数衰减越快,同时水平纵向相关系数在一定的纵向距离内会保持一个更大的数值波动;当浅海声速在不同的负声速梯度变化下,在水体上层海表面声线分布的变化相对于等声速梯度环境下变化微弱,使得负声速梯度值的大小对水平纵向相关系数的衰减无太大影响。
2.2.2 不同声速分布下声场水平纵向相关长度分析
在讨论不同声速分布下声场水平纵向相关系数变化规律的基础上,图10、11讨论了在仿真的浅海低频环境下,不同声速分布下声场水平纵向相关长度的变化规律。图10给出了海水层表面声速在1 500 m·s-1时,随着海水层底部声速变化(1 480~1520 m·s-1),水平纵向相关长度的变化曲线。图11给出了海水层表面声速在1 520 m·s-1时,随着海水层底部声速变化(1 500~1 540 m·s-1),水平纵向相关长度的变化曲线。
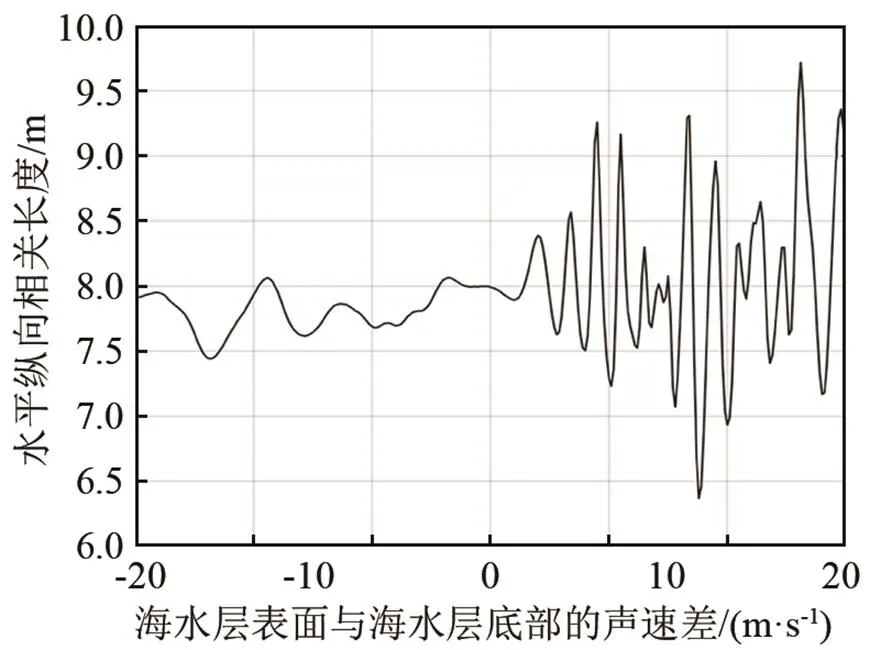
图10 海水层表面声速在1 500 m·s-1,在不同海水层底部声速下水平纵向相关长度的变化曲线
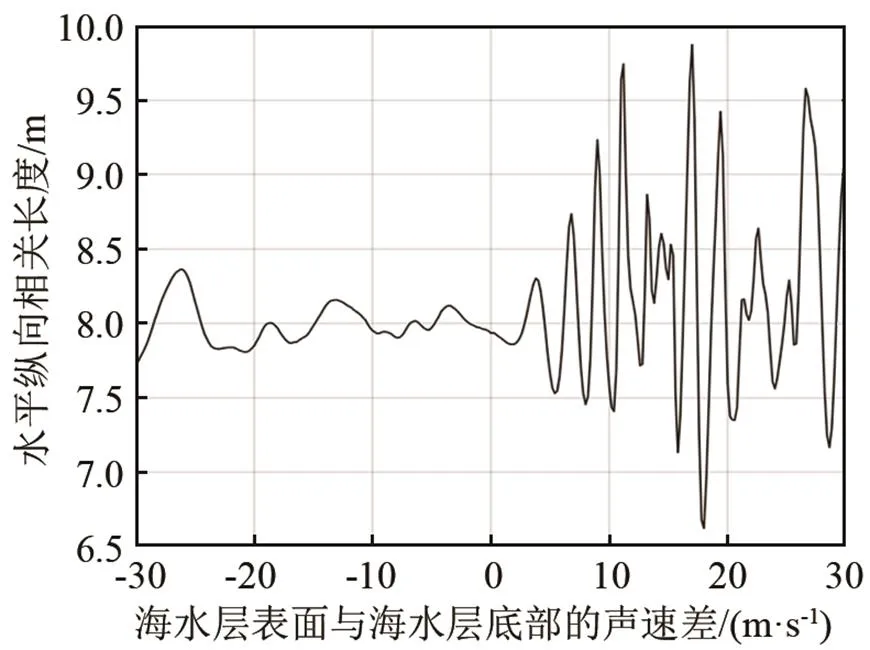
图11 海水层表面声速在1 520 m·s-1,在不同海水层底部声速下水平纵向相关长度的变化曲线
通过图10、11的对比可以发现,水平纵向相关长度的变化,均以在等声速海洋环境下的水平纵向相关长度数值为中心,呈现水平上下起伏;正声速梯度下的起伏频率比负声速梯度下更高,同时起伏幅度也比在负声速梯度更大。当海水层表面声速在1 500 m·s-1时,图10中正声速梯度情况下的水平纵向相关长度在6.4~9.8 m之间波动;在负声速梯度下的水平纵向相关长度在7.6~8.2 m之间波动。当海水层表面声速在1 520 m·s-1时,正声速梯度情况下的水平纵向相关长度在6.6~9.9 m之间波动;在负声速梯度下的水平纵向相关长度在7.7~8.4 m之间波动。可见,随着海水层表面声速的增大,水平纵向相关长度的波动范围会有所变化。
3 结论
本文采用基于抛物线方程的RAM模型,讨论分析了在所仿真的浅海低频环境下,频率范围在100~200 Hz,声源深度为50 m,参考阵元位置深度为20 m、距离声源30 km处,不同海洋垂直声速变化环境对浅海低频声场的垂直相关以及水平纵向相关的影响,得到的结论如下:
(1) 对于浅海低频声场的垂直相关性,当浅海低频声场处于正声速梯度时,声速梯度值越大,水体下层的声线分布越分散,声场的干涉结构越简单,垂直相关系数衰减得越慢;垂直相关长度随着正声速梯度的增加,呈现剧烈的起伏上升趋势。而当浅海低频声场处于负声速梯度时,负声速梯度越大,水体下层的声线分布越集中,声场的干涉结构越复杂,垂直相关系数衰减得越快;其垂直相关长度随着负声速梯度强度的增加,呈现缓慢的摆动下降趋势。
(2) 对于浅海低频声场的水平纵向相关性,当浅海低频声场处于正声速梯度时,正声速梯度越大,水体上层海表面处的声线分布越集中,声场的干涉结构越复杂,水平纵向相关系数衰减得越快,同时在一定的参考阵元与接收阵元距离内会出现较大的波动;其水平纵向相关长度随着正声速梯度的增加,呈现剧烈的水平上下波动。当浅海低频声场处于负声速梯度时,随着负声速梯度的增大,水体上层海表面处的声线分布越分散,声场的干涉结构越简单,水平纵向相关系数衰减得越缓慢;其水平纵向相关长度随着负声速梯度强度的增加,呈现缓慢的水平上下波动。
考虑在实际浅海环境实验中,由于风浪作用、海水温度变化、盐度改变等一系列原因,使得浅海的声速剖面在不同时期会呈现不一样的分布特征。而声速分布的变化,将明显影响水听器阵列在应用时的阵增益效果及抗干扰能力。本文的研究表明,对于垂直方向上布放的阵列,在正声速梯度环境下,阵列能获得相较于在负声速梯度以及等声速梯度环境下更强的阵增益,对噪声信号的抗干扰性更高;而对于水平纵向方向上布放的阵列,在正声速梯度环境下,阵列获得的阵增益相对于在负声速梯度以及等声速梯度环境下获得的阵增益要弱,但是能在较长的阵元间隔下保持一定的阵增益;梯度值越大,上述影响的规律性越强。在负声速梯度浅海环境下,当接收阵元间隔相同时,声速梯度对阵列工作性能的影响则相反。
[1] URICK R J, 洪申译. 水声原理[M]. 3版. 哈尔滨: 哈尔滨工程大学出版社, 1990.
URICK R J. Principles of underwater Sound[M]. 3rd. Translate: HONG S. Harbin: Harbin Engineering University Press, 1990.
[2] WANG Q, ZHANG R H. Sound spatial correlations in shallow water[J]. J. Acoust. Soc. Am., 1992, 92(2): 932-938.
[3] GALKIN O P, POPOV R Y, SEMENOV Y V, et al. Spatial correlation of the sound field in an ocean shelf zone[J]. Acoustical Physics, 2011, 47(5): 534-539.
[4] 苏晓星, 李风华, 简水生. 浅海低频声场的水平纵向相关性[J]. 声学技术, 2007, 26(4): 579-583.
SU Xiaoxing, LI Fenghua, JIAN Shuisheng. Horizontal-longitudinal correlations of low-frequency acoustic field in shallow water[J]. Technical Acoustics, 2007, 26(4): 579-583.
[5] 宫在晓. 浅海声信道的水平相关与声场匹配定位[J]. 声学技术, 2003, 22(s2): 95-97.
GONG Zzaixiao. Horizontal correlation and MFP in shallow water sound channel[J]. Technical Acoustics, 2003, 22(s2): 95-97.
[6] 邵炫, 孙超, 李明杨. 基于WARPING变换的宽带目标检测[C]//2014年中国声学学会全国声学学术会议论文, 2014.
[7] 赵梅, 胡长青. 浅海倾斜海底声场空间相关性研究[J]. 声学技术,2010, 29(4): 365-369.
ZHAO Mei, HU Changqing. Study of the sound spatial correlation in shallow water with inclined seafloor[J]. Technical Acoustics, 2010, 29(4): 365-369.
[8] 赵梅, 胡长青. 浅海低频声场垂直相关与海底参数反演[J]. 声学技术, 2010, 26(4): 579-583.
ZHAO Mei,HU Changqing. Sound vertical correlation and the sea-bed parameters inversion in shallow water with inclined seafloor. Technical Acoustics, 2010, 29(6): 112-113.
[9] RAFAELY B. Spatial-temporal correlation of a diffuse sound field[J]. J. Acoust. Soc. Am., 2000, 107(6): 32-54.
[10] 宋军, 张刚强. 浅海声场的垂直相关性及垂直阵的空间增益分析[J]. 声学技术, 2014, 33(5): 220-223.
SONG Jun, ZHANG Gangqiang. Analysis of sound field vertical corre-lation property and spatial gain of vertical array in shallow wa-ter[J]. Technical Acoustics, 2014, 33(5): 220-223.
[11] 季桂花, 李整林. 南海线性内波条件下的匹配场时间相关长度[J]. 声学学报, 2011, 36(1): 1-7.
JI Guihua, LI Zhenghlin. The coherence-time of matched-field processing with the presence of the linear internal waves in the South China Sea[J]. Acta Acustica, 2011, 36(1): 1-7.
[12] 邵炫, 孙超. 陆架斜坡海域信号水平纵向相关特性实验研究[J]. 中国科学: 物理学力学天文学, 2016, 46(9): 1-4.
SHAO Xuan, SUN Chao. Experimental study on horizontal longitudinal correlation of the signal at continental slope area[J]. Sin-Phys Mech Astron, 2016, 46(9): 1-4.
[13] COLLINS M D. User’s guide for RAM versions 1.0 and 1.0p[J]. Naval Research Laborator.
[14] 陈勃, 赵梅, KLUSEK Z, 等. 一种简单的浅海环境噪声场垂直相关模型[J]. 声学技术, 2015, 34(6): 127-130.
CHEN Bo, ZHAO Mei, KLUSEK Z, etc. A simple model of vertical coherence of ambient noise in shallow water[J]. Technical Acoustics, 2015, 34(6): 127-130.
Influences of velocity profiles on the spatial correlation of low-frequency sound field in shallow water
ZHU Jun1, ZHU Han-hao2, QU Ke3, ZHENG Guang-xue2, HU Jia-chen2
(1. Institute of Naval Architecture and Mechanical-Electrical Engineering, Zhejiang Ocean University, Zhoushan 316022, Zhejiang, China;2. Institute of Marine Science and Technology, Zhejiang Ocean University, Zhoushan 316022, Zhejiang, China;3. College of Electronics and Information Engineering, Guangdong Ocean University, Zhanjiang 524088, Guangdong, China)
Aiming at the influence of velocity profiles on the spatial correlation of low-frequency sound field in shallow water, the variation of spatial correlation under different velocity gradients and different array element intervals is simulated and analyzed by using the RAM program, which is based on the parabolic equation. Simulation results show that with the increase of positive velocity gradient, the vertical correlation coefficient decays more slowly and the horizontal-longitudinal correlation coefficient decays faster, both the vertical and the horizontal-longitudinal correlation lengths fluctuate violently; with the increase of the negative velocity gradient, the vertical correlation coefficient decays faster and the horizontal-longitudinal correlation coefficient decays more slowly, the correlation length of both types fluctuates slowly.
shallow water sound field; parabolic equation; velocity profiles; spatial correlation
TB566
A
1000-3630(2019)-04-0376-06
10.16300/j.cnki.1000-3630.2019.04.003
2018-03-07;
2018-04-16
国家自然科学基金资助项目(11704337);浙江省海洋观察-成像试验区重点实验室资助项目(00IT20170F01);浙江省教育厅科研项目(Y201738505)
朱军(1995-), 男, 广东深圳人, 硕士研究生, 研究方向为水声工程。
屈科,E-mail: quke09@mails.ucas.ac.cn
