基于四元十字阵的低频换能器指向性检测方法
2019-09-02郭世旭朱锰琪王萧博王月兵赵鹏杨民
郭世旭,朱锰琪,王萧博,王月兵,赵鹏,杨民
基于四元十字阵的低频换能器指向性检测方法
郭世旭1,朱锰琪1,王萧博2,王月兵1,赵鹏1,杨民3
(1. 中国计量大学,浙江杭州 318000;2. 浙江省计量科学研究院,浙江杭州 310018;3. 哈尔滨工程大学,黑龙江哈尔滨 15000)
针对大型低频换能器指向性难以测量的问题,提出了一种基于四元十字阵的测量方法以获取大型低频换能器的指向性。利用到达四元十字阵阵元的时延差信息,结合双曲面交汇法对换能器进行定位,并根据四元十字阵阵元测得的声信号实现大型低频换能器指向性的测量;对定位算法进行理论仿真,设计并进行了湖上试验以测量模拟声源的指向性;对湖上试验测量数据进行计算分析,并与模拟声源在消声水池中的测量结果进行比较,两者-3 dB波束开角的测量结果相差在10%以内。此方法可以用于低频换能器指向性的测量。
低频换能器;指向性;四元十字阵;双曲面交汇法;时延差
0 引言
海洋勘探是人们了解海洋的主要手段,低频换能器在海洋勘探领域中对探潜、测深、避障、探雷等方面起重要作用[1]。实际使用中低频换能器发射声波,并根据反射声波的时间延迟、方位和强度等信息实现对目标的识别和探测[2]。对于低频换能器而言,指向性是衡量其是否具有规定分辨率的重要指标[3]。指向性越尖锐,声能在声轴方向上的集中度越高,越有利于增加低频声波的作用距离。因此,准确获取低频换能器的指向性对其在海洋勘探领域中的应用具有重要意义。
低频换能器指向性测量通常是在实验室消声水池(或湖上)利用一个标准水听器与之配合,通过转动低频换能器改变其与标准水听器的方位关系,测量不同角度下的声压信号来测量低频换能器的指向性[4]。但是随着低频换能器向大功率、大尺寸的方向发展,标准测量方法不能满足其指向性测试的要求,进而出现近场测量法[5]、基于激光测振技术、赫姆霍兹积分法[6]和边界元法[7]的测量方法。近场测量法存在测量面较难选取和空间分辨力低的问题。基于激光测振技术和边界元法的测量方法在测水中换能器表面振动时,由于声光作用现象的存在,激光测振仪得到的测量结果并不能精确反映换能器表面真实振动的情况,从而造成误差。
为了解决大型低频换能器指向性难以测量的问题,本文提出了一种基于四元十字阵的测量方法,该方法将标准测量方法中待测换能器的转动改为平动,利用四元十字阵的时延差对换能器进行定位,确定十字阵阵元与换能器的相对方位关系,进而确定换能器的指向性。本文首先阐述了指向性图的测量方法以及基于四元十字阵双曲交汇法对换能器定位的原理;又依据设计的测量方案,对十字阵阵元间距的选取进行了理论仿真;对本文提出的方法进行了湖上测量实验,并对待测换能器进行了水池校准实验,分别得到了指向性图与波束开角,通过对比,验证了本文提出方法的可行性。
1 基于四元十字阵的指向性测量原理
1.1 指向性图与波束宽度
指向性图是描述一个换能器指向性响应的重要特征参量[8]。对于一个低频换能器而言,指向性图是表示其在自由场中辐射声波时,在其远场的声能空间分布图像,通常对单一平面内的指向性进行测量并绘制指向性图。指向性的测量示方法如图1所示,测量时以低频换能器为声中心,以测试距离为半径测量其圆周上测量点的声压值。以测量点到换能器中心的连线与主声轴的夹角为横坐标,以测量点的声压值为纵坐标,即可绘制低频换能器的指向性图。确定低频换能器与测量水听器的位置关系即可确定其在测量平面内的指向性。

图1 指向性测量示意图
波束宽度是指向性图的重要特征参量,也是换能器性能的重要参数。波束宽度是指主瓣或者主声束两侧的两个方向之间的夹角,通常取这两个方向上的声压级相对于声轴声压级下降3 dB时的夹角,称为-3 dB的波束宽度。根据指向性图,则可确定低频换能器-3 dB的波束宽度。


对应的角度可以表示为
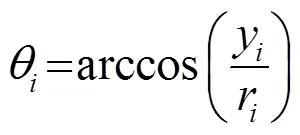

图2 换能器与水听器测量点之间的位置关系示意图
1.2 基于四元十字阵的双曲交汇定位法
常规的四元十字阵定位方法是基于准确的时延来进行定位[9],但在实际的测量中,由于难以保证信号发射端与接收端的脉冲同步,造成时延估计的误差较大,对定位的准确度影响较大。因此,采用一种利用时延差对声源进行定位的定向定位方法,即双曲交汇法来提高定位精度[10-11]。


通过将声源发出的声波传播到不同阵元的时间差转化为声源到不同阵元的距离差,依次建立双曲面方程。则3个双曲面相交必有一个交点。若声源坐标和时延差测量准确,则可求得准确点,但在实际测量过程中,由于时延差测量误差的存在,只能求得最近似的解,通常的方法是将该非线性方程组线性化求取最小二乘解,该算法必须要满足非奇异矩阵的要求,因此通常采用到阵列中心距离相等的四元十字阵。
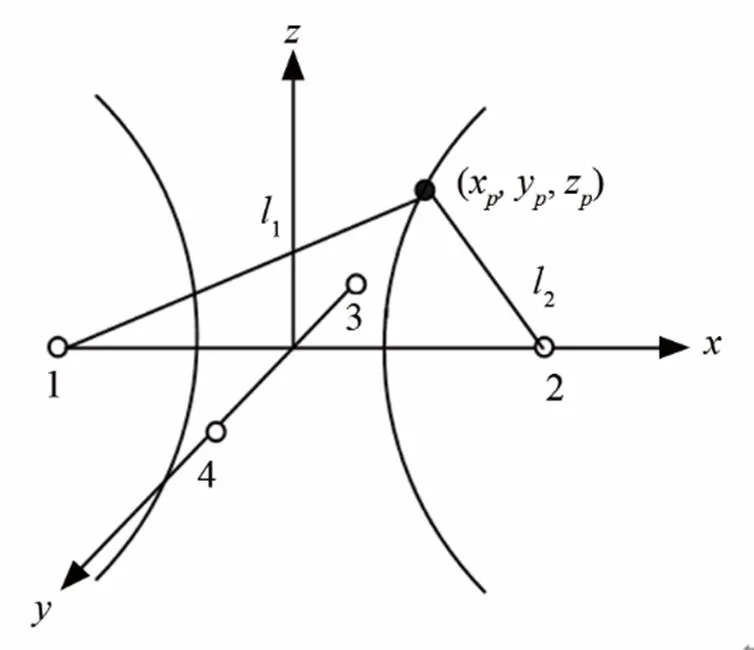
图3 双曲交汇示意图
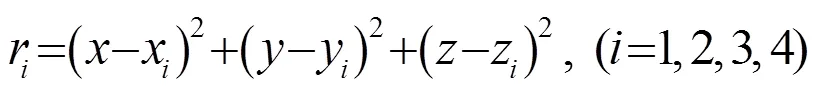
则声源到不同阵元和到参考阵元的距离差可以表示为
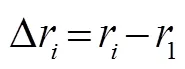
对式(5)整理,有:

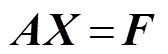
选择合适的阵元坐标,使A为满秩,利用最小二乘法求解则

2 理论仿真
四元十字阵的阵元间距对于定位算法的准确度存在影响,基于本文提出的测量方法,对定位算法进行仿真以确定四元十字阵的阵元间距。假设低频换能器在水下以1 m·s-1的速度匀速移动,四元十字阵固定不动,测试平面与阵元所在平面的距离为10 m,低频换能器与四元十字阵的中心处于同一高度,各测量点的空间坐标已知。选取不同的阵元间距,假定接收到的信号为10个5 kHz的脉冲信号,再结合80 kHz的采样率模拟每一个阵元的接收信号。对接收信号用修正的前沿检测法[13]进行处理获取精确的时延差,代入双曲面交汇定位算法中,仿真结果如图4所示。
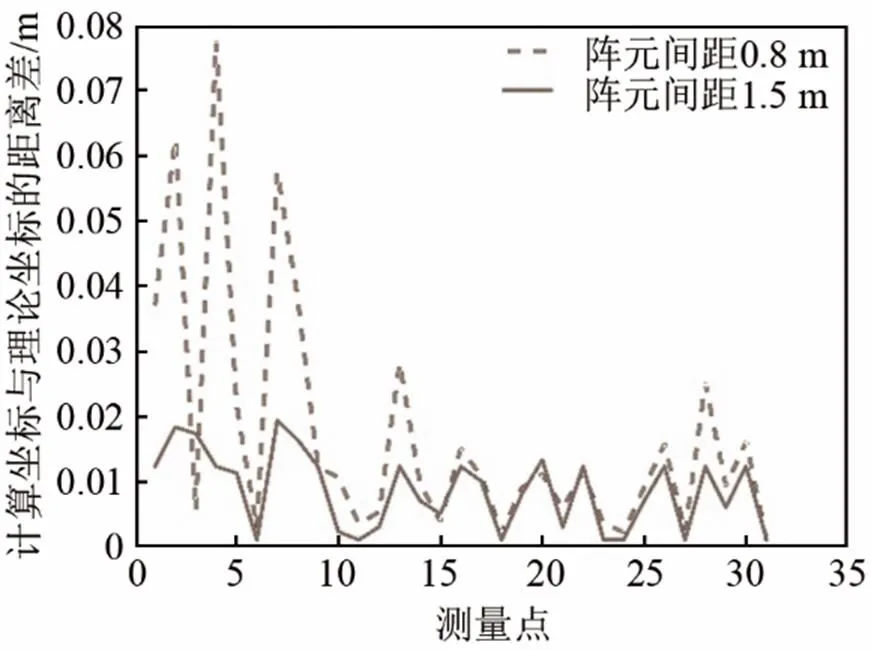
图4 不同阵元间距的仿真结果图
图4中虚线表示阵元间距为0.8 m时的误差值,实线表示阵元间距为1.5 m时的误差值。由仿真结果可以看出,阵元间距为0.8 m时采用双曲面交汇法产生的定位误差较小,计算值与理论值的最大距离误差为0.077 4 m,定位误差为0.77%。当扩大阵元的间距至1.5m时,计算值与理论值的误差进一步缩小,最大误差为0.038 5 m,定位误差为0.39%,可见阵元间距越大,定位精度越高。但在实际使用过程中,阵元间距过大会造成四元十字阵使用不便,因此,四元十字阵的间距选取1.5 m。
声源在水下沿直线匀速移动时,会随着水体流动而移动,且移动是无规则的,即可能上下波动,也可能朝四周移动。对于这种情况的仿真结果如图4所示。由仿真结果可以看出,计算值与理论值较为接近,最大误差为0.113 4 m,定位误差为1.1%,远小于水声定位10%的误差要求。从仿真效果可以得出,双曲面交汇法的定位精度较高,即使声源做无规则运动,定位也十分准确,也无需测量准确时延,可以用于实际测量。

图5 实际海况下声源出现颠簸的仿真结果图
3 试验研究
为验证基于四元十字阵的换能器指向性测量方法的效果,采用直径14 cm、高30 cm的圆柱形换能器作为待测换能器,分别在某水库和实验室消声水池(标准测量法)中对圆柱形换能器的指向性进行了测量,并对两种测量结果进行比较。
3.1 湖上试验
在湖试中用基于四元十字阵的换能器指向性测量方法对待测换能器的指向性和波束开角进行测量。
测量系统如图6所示,主要包括信号源、功率放大器、前置放大电路、FPGA采集存储电路等。试验时,计算机经Labview程序控制信号源每秒发出10个频率为5 kHz的正弦脉冲信号,经功率放大器放大,加载到待测低频换能器发射声波。四元十字阵阵元接收到的信号经放大,传输到FPGA中再传输到计算机。与标准测量法相比,本测量方法利用待测换能器的平动代替转动实现换能器指向性的测量,测量示意图如图7所示。四元十字阵竖直悬挂于水中固定不动,其阵中心位于水下5 m,待测换能器通过绳子从电瓶船的一端放至水下5 m并通过待测换能器底部吊装铅鱼保持其水下姿态稳定,测量时在正对四元十字阵15 m的平面内,载有待测换能器的电瓶船以最低速度(约1 m·s-1)沿直线匀速行驶,到达预定测量区域时进行数据采集,直至驶离测量区域。期间待测换能器每秒发射10个频率为5 kHz的正弦脉冲信号,四元十字阵阵元的采样率为80 kHz。
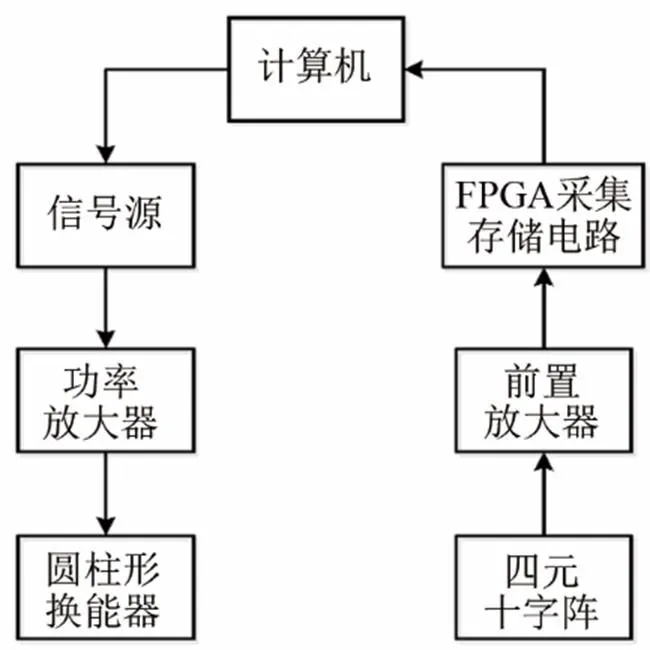
图6 测量系统流程图

图7 湖上试验测量示意图
3.2 模拟声源水池校准实验
在实验室消声水池中,对圆柱形换能器采用标准测量法(如图1)进行测量,测得圆柱形换能器5 kHz时的指向性图如图8中绿色曲线所示。其-3 dB的波束开角为61°。

图8 不同阵元测得指向性结果与实验室测得结果对比图
3.3 测试结果
图9为湖上试验时求得的圆柱形换能器的运动轨迹,将其代入指向性的计算公式测量结果中进行指向性图的绘制。
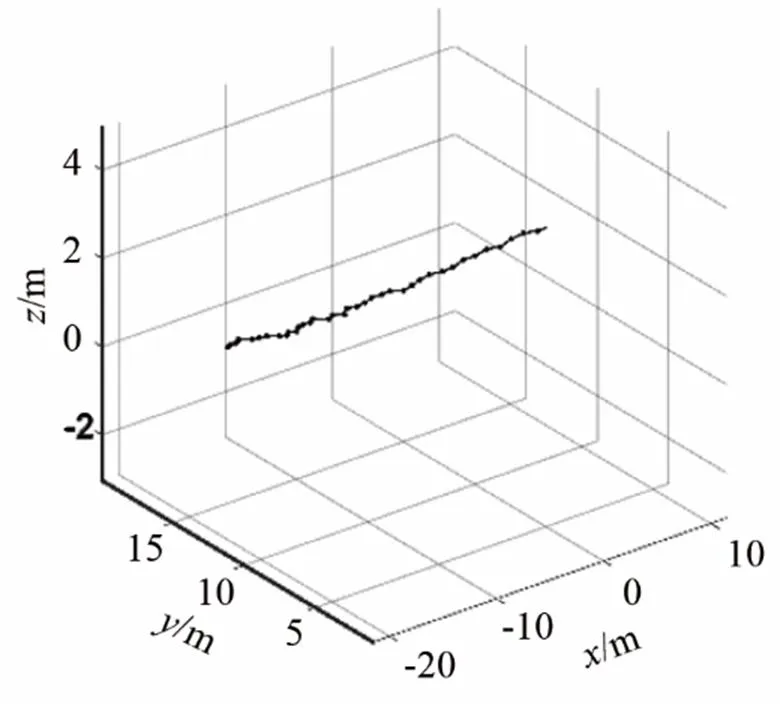
图9 圆柱形换能器运动轨迹图
图8中的1、2、3、4号阵元为湖试指向性测量结果,从图8中可以看出,1号阵元、2号阵元、3号阵元测得的声源指向性曲线较为接近,其-3 dB波束开角分别为58°、57°、57°,与在实验室消声水池中测的-3 dB波束开角为61°对比,计算得误差分别为4.9%(-0.436 dB)、6.5%(-0.584 dB)、6.5%(-0.584 dB),在《声学水声换能器测量》国标中对波束角不确定度要求的误差10%(±1 dB)之内[14]。图8水池测量结果中,当波束角为30°时,声压相对于主声轴上声压下降了2.5 dB,湖试实验中3个阵元测量结果与其相一致。
由测量结果可知,基于四元十字阵的指向性测量方法与标准测量方法相比,测量误差在6.6%之内。不同阵元测得的换能器指向性曲线和波束开角一致。测量结果并非偶然,初步判断测量方法是可行的。由试验结果图得出本测量方法与实验室标准测量方法存在一定的误差。经过分析,试验误差产生的主要原因有以下几点:
(1) 圆柱形换能器是由绳子吊放至指定位置,实际开船过程中,受到水流的影响,水下姿态发生改变,与测量阵列产生夹角,从而产生测量误差。
(2) 本文采用的定位方法是基于时延差的双曲面交汇法,时延差的准确测量是定位的关键,时延差测量不准会使建立的双曲面模型与实际模型发生偏差,造成定位误差,影响测量结果。
(3) 本试验中四元十字阵采取的是硬质金属杆连接,将阵列吊放至水下相应位置。由于金属杆会对声波进行反射,造成水听器测得的声压不只是直达波声压,对水听器测得的声压值产生影响,从而影响指向性的测量结果。而4号阵元与金属杆相邻,4号阵元测得的是直达波与反射波的叠加声压,造成4号阵元的测量结果与其余3个相比误差较大。
4 结论
与现有的换能器指向性测量方法相比,本文提出的测量方法有以下优点:将现有测量法中的转动换能器改为平动,解决了换能器实船安装后声学特性无法检测和换能器尺寸变大测量困难的问题。随着换能器向大尺寸、低频率方向发展,现有的水池测量环境很难满足换能器指向性的测量条件,本文提出的测量方法受传统测量方法的启发,通过双曲面方位交汇法测得换能器的位置,对换能器的指向性进行测量。与水池中换能器标准的校准方法相比,测量误差在10%之内,且本方法在测量过程中,不需要特殊的转动装置,仅需连续直线运动即可。本方法可应用于大尺寸低频换能器在装船后,在开阔水域的指向性测量,且测量效率较高。
本文提出的方法需要换能器保持较为稳定的姿态,因此对开阔水域的环境条件要求较高,如水下尽可能流场平稳,挂载换能器的小船尽可能以低速行驶;另外,本文仅在湖上验证了本方法的可行性,在实际的海洋区域,海水的密度、温度、海流等因素是否会对测量结果产生影响还不确定。本方法对低频换能器指向性的测量效果还有待海试的进一步验证。
[1] 靳建嘉. 低频换能器及校准技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
JIN Jianjia. Research on low frequency transducer and calibration technology[D]. Harbin: Harbin Engineering University, 2011.
[2] 刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010.
LIU Bosheng, LEI Jiayu. Principles of underwater sound[M]. Harbin: Harbin Engineering University Press, 2010.
[3] 卢逢春, 张殿伦, 田坦, 等. 高分辨图像声纳预成多波束的指向性湖上测量方法[J]. 哈尔滨工程大学学报, 2003, 24(5): 505-507.
LU Fengchun, ZHANG Dianlun, TIAN Tan, et al. Measurement of directivity on lake for multi-beam high resolution image sonar system[J]. Joumal of Harbin Engineering University, 2003, 24(5): 505-507.
[4] 赵鹏涛, 蒋世军. 某水下平台水听器的指向性计算与水池测试[J].声学技术, 2013, 32(S1): 293-294.
ZHAO Pengtao, JIANG Shijun. Numerical computation and experimental test of directivity of hydrophone[J]. Technical Acoustics, 2013, 32(S1): 293-294.
[5] 赵涵, 平自红. 近场测量方法研究[J]. 声学与电子工程, 1996(2): 39-43.
ZHAO Han, PING Zihong. Study of near-field measurement methold[J]. Acoustics and Electronics Engineering, 1996(2): 39-43.
[6] WILLIAMS E G. Regularization methods for near-field acoustical holography[J]. J. Acoust. Soc. Am., 2001, 110(4): 1976-1988.
[7] 王世全, 王月兵, 刘百峰. 基于激光测振技术和边界元方法的声源指向性计算[J]. 声学与电子工程, 2006(3): 14-18.
WANG Shiquan, WANG Yuebing, LIU Baifeng.Directivity calculation of acoustic source based on laser vibration measurement and boundary element method[J]. Acoustics and Electronics engineering, 2006(3): 14-18.
[8] 郑士杰. 水声计量测试技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 1995.
ZHENG Shijie. Underwater acoustic metrology and measurement technology[M]. Harbin: Harbin Engineering University Press, 1995.
[9] 王伟. 基于时延估计的被动声定位研究[D]. 长沙: 国防科学技术大学, 2010.
WANG Wei. Acoustic location based on time dealy estimation[D]. Changsha: National University of Defense Technology, 2010.
[10] LIU C F, YANG J, WANG F S. Joint TDOA and AOA location algorithm[J]. Journal of Systems Engineering and Electronics, 2013, 24(2): 183-188.
[11] 徐菲. 基于时延估计的四元十字阵被动定向近似误差分析[J]. 电子测量技术, 2014, 37(12): 29-31.
XU Fei. Approximate error analysis of acoustic passive localization with cross array based on time delay estimation[J]. Electronic Measurement Technology, 2014, 37(12): 29-31.
[12] 王玲, 魏星, 万建伟, 等. 基于TDOA定位算法的模糊解消除方法[J]. 计算机工程与科学, 2006, 28(3): 74-75.
WANG Ling, WEI Xing, WAN Jianwei, et al. A method of elimination ambiguous solutions based on the TDOA algorithm[J]. Computer Engineering and Science, 2006, 28(3): 74-75.
[13] 薛夫连, 梅继丹, 孙大军. 被动声呐脉冲检测时延估计方法研究[J]. 声学技术, 2015, 34(2): 376-378.
XUE Fulian, MEI Jidan, SUN Dajun. A study on time delay estimation method of passive sonar pulse detection[J]. Technical Acoustics, 2015, 34(2): 376-378.
[14] 中华人民共和国国家质量监督检验检疫总局. GB/T7965-2002声学水声换能器测量[S]. 北京: 中国标准出版社, 2002.
A method of directivity measurement based on four-element cross array
GUO Shi-xu1, ZHU Meng-qi1, WANG Xiao-bo2, WANG Yue-bing1, ZHAO Peng1, YANG Min3
(1. China Jiliang University,Hangzhou 318000, Zhejiang, China; 2. Zhejiang Province Institute of Metrology, Hangzhou 310018, Zhejiang, China;3.Harbin Engineering University,Harbin 150001, Heilongjiang, China)
Aiming at the problem that the directivity of large low frequency transducer is difficult to measure, a measurement method based on four-element cross array is proposed in this paper. By measuring the time delay differences between the four-elements of the cross array and combining with the hyperboloid intersection method to locate the transducer, the measurement of the directivity of large low frequency transducer can be realized by measuring the acoustic signals received by the four-elements of the cross array. The transducer locating algorithm is simulated according to the measurement method, and the corresponding lake experiment is designed for measuring the directivity of the simulated sound source based on this method. The measurement results are analyzed and compared with the results of the laboratory measurement method in anechoic tank. It is shown that the difference between both measurement results of -3dB beam width is within 10%, and so this method can be used for testing the directivity of large low frequency transducer in modern sonar equipment.
low frequency transducer; directivity; four-element cross array; hyperboloid convergence method; time delay
TB565.1
A
1000-3630(2019)-04-0464-06
10.16300/j.cnki.1000-3630.2019.04.018
2018-08-15;
2018-10-19
国家重点研发计划(2017YFF0206403)
郭世旭(1987-), 男, 河南平顶山人, 硕士生导师, 研究方向为为海洋声学计量检测技术研究。
朱锰琪,E-mail: 934302321@qq.com
