仿生复眼系统的子眼安装孔对准误差检测方法

张 广，王新华，李大禹

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.吉林大学 计算机科学与技术学院，长春 130012)

1 引 言

随着光学成像技术的不断发展，实现大视场和高分辨率的信息收集与记录一直是光电成像系统追求的目标。由于光学系统的复杂程度与系统传输的总信息量成正比，因此对传统光电成像系统而言，不可能同时大幅提高成像视场和分辨率。受昆虫复眼结构的启发，仿生复眼光学系统应运而生，并逐渐成为国内外的研究热点，此类系统由多个独立的子眼成像系统构成，每个子眼对目标物分别成像，彼此之间相互独立互不干扰，最后将所有子眼图像进行拼接融合处理，即可获得大视场无缝拼接图像。这种系统可以很好地解决传统光学系统存在的大视场、长焦距、小体积和高分辨率的矛盾，并广泛应用于航空侦查、舰载预警、边海防、广场校园监控等诸多领域[1-4]。

针对广域范围内微小目标快速获取和精准跟踪的应用需求，本课题组设计了由一级同心物镜和二级子眼镜头阵列组成的大视场高分辨率仿生复眼成像系统。为实现全视场高分辨率图像的精准无缝拼接，必须严格保证所有子眼镜头的安装孔轴线与同心物镜球心的对准误差在光学设计允许公差范围内，否则极有可能遗漏部分图像信息[5-7]。目前针对多孔多光轴系统的对准误差，暂无特定的检测设备和方法。对于传统的多孔结构，可使用位置量规对孔的尺寸和位置公差进行检测，但检测精度低，无法衡量孔的轴线与参考中心的对准情况。三坐标测量机可对孔的尺寸及形位公差进行精确测量与分析，但若用于仿生复眼系统的子眼安装孔对准误差检测，则需要建立特定的坐标系并将同心物镜球心作为坐标系原点，选择合适的探针获取安装孔内壁多个位置的三维坐标值，最后通过多点测量拟合出每个子眼镜头的光轴。整个检测方法复杂，而且同心物镜的真实球心与三坐标测量机定义的原点即虚拟球心不可避免地存在安装误差，此项误差难以准确衡量，这将严重影响各子眼安装孔对准误差检测结果的准确性[8-9]。近年来，长春理工大学通过两个高精度徕卡经纬仪互瞄的方法实现了仿生复眼系统各子眼光轴夹角的测量[10]，但若将其用于本文基于同心物镜式的仿生复眼系统的对准误差检测，必须配合高精度二维直线导轨以保证发光经纬仪出射光充满每个子眼的入瞳，从而导致检测硬件造价昂贵。此外，还要将成像系统与经纬仪转换到同一坐标系下，并综合考虑坐标转换误差、导轨直线度误差、导轨与经纬仪配合误差等多种误差源对总体误差的影响，整个数学建模和评价过程过于繁琐复杂。

为解决仿生复眼系统子眼镜头光轴对准难题，本文基于PSM(point source microscope)装调定位仪的自准直原理，通过转接器将PSM分别固定在球形穹顶的所有子眼镜头安装孔中，计算经同心物镜反射后像点质心偏离量与安装孔轴线对准误差的关系，并利用Lighttools软件仿真检测光路，实现对所有安装孔对准误差的检测。该检测方法简单实用，可为所有子眼镜头光轴与同心物镜球心的对准情况提供参考，从而实现所有子眼图像的高精度无缝拼接。

2 系统的构成及其工作原理

2.1 仿生复眼系统的构成

图1为仿生复眼系统结构示意图，第一级成像系统是一个三胶合同心物镜光学系统，由它将大视场的探测目标完全一致地成像在一个球形焦面上(第一像面)，再由38个子眼镜头构成的第二级成像系统将球形焦面成像到相应的CMOS探测器上。由于这种仿生复眼结构的特异性，第一级同心物镜系统可被看作一个无光轴系统，即每一条通过球心的直线都可看成物镜的光轴。为保证整个视场范围内成像的一致性，使得每个子眼所成图像都能有足够且准确的重叠区域进行计算拼接，从而获得无缝拼接的大视场高分辨率图像，每个子眼镜头的光轴必须精准地穿过同心物镜的球心。

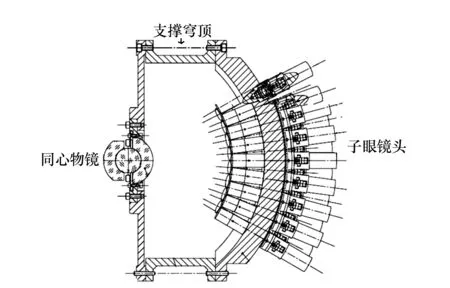
图1 仿生复眼系统示意图 Fig.1 Diagram of bionic compound eye system

2.2 PSM系统的构成及工作原理

PSM装调定位仪是美国亚利桑那大学光学中心研制的高精度辅助装调工具，可帮助确定光学元件各个表面的曲率中心位置，从而完成光学系统各元件与基准轴的校准，校准精度可达亚微米级，其对仿生复眼成像系统子眼安装孔对准误差检测的影响可忽略不计[11]。本课题组在2014年采购了该仪器，并用于复杂3D光学系统的辅助装调。PSM的结构及工作原理如图2所示，其中激光二极管作为点光源(Point light source)，准直后经反射镜(反射镜)折转到分光镜(Splitter)上，由物镜(Objective lens)将准直平行光汇聚到物镜焦点处。理想情况下，当待测球面的曲率中心与物镜焦点重合时，光线经待测表面反射沿原路返回，由管镜(Tube Lens)汇聚在成像器件(CCD camera)靶面中心。而当待测表面曲率中心与物镜的焦点不重合时，光线经待测面反射后无法原路返回，通过管透镜汇聚在CCD相机的靶面，会形成偏离靶面中心的返回像光斑。由于PSM在实际加工和装配过程中，无法精确保证点光源、分光镜、管镜、物镜和CCD相机都处于同一基准轴线，这样即使待测表面曲率中心与物镜的焦点重合，返回像光斑也不可能成像在CCD靶面中心。因此，必须首先确定PSM返回像的基准零位，消除PSM内部元件加工和装调误差对待测元件检测结果的影响。

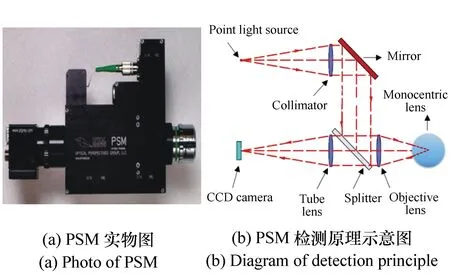
图2 PSM实物图及原理示意图 Fig.2 Photo of PSM and detection principle diagram

PSM的辅助装调过程与激光偏心测量仪类似[12]，利用激光偏心测量仪进行光学系统装检时，光学系统通过三爪卡盘固定于高精度气浮转台上，通过旋转气浮转台，使返回像光斑作划圆运动，通过拟合划圆直径即可获取每个光学表面相对于最佳拟合光轴的偏心量[13]。然而，当利用PSM进行仿生复眼系统的子眼镜头安装孔对准误差检测时，由于同心球透镜无法精确旋转，检测过程无法通过传统方法实现。因此，需要研究一种利用PSM作为辅助工具，实现对子眼安装孔对准误差进行检测的有效方法。

3 检测方法

3.1 PSM基准参考零位的确定

基于PSM的结构特点和仿生复眼系统的成像原理，确定子眼镜头安装孔对准误差的检测方法如下：首先将PSM分别固定在支撑穹顶的所有子眼镜头安装孔中，然后在CCD相机上获取经同心物镜反射后的返回像点，并求取该像点的质心位置，计算其与基准参考零点的偏离量，再推导此偏离量与子眼安装孔轴线对准误差的几何关系，并利用Lighttools软件对检测光路进行仿真分析和实验验证。

确定PSM基准参考零位的实验如图3所示。此处有必要说明的是，在理想情况下，PSM物镜的焦点应与待测同心物镜的球心重合，如图2(b)所示。因此，需要根据子眼镜头支撑穹顶的半径，确定合适焦距的物镜，保证检测过程中返回像弥散斑直径最小。由于仿生复眼结构的支撑穹顶半径为260 mm，选择通光孔径为25.4 mm，焦距为300 mm的双胶合透镜作为PSM的物镜，并设计加工与之匹配的转接器。需要注意的是通过转接器将PSM固定在穹顶安装孔时，要在轴向保留一定的微调余量，以保证利用自准直法产生的PSM返回像点最小。实现对子眼安装孔轴线对准误差的精确检测，原则上即便无法满足精确检测的共焦条件，转接器加工的高精度和后续质心探测算法的高精度也足以保证返回像点的质心位置偏差不会影响测量结果的准确性。

图3 返回像点基准参考零位实验图 Fig.3 Experiment of determining the reference zero position

在确定PSM基准零位的实验中，调节位移台和升降台，将物镜的焦点调节至漫反射镜的大致中心位置，在CCD相机中观测光线经漫反射镜返回像点。根据PSM的出厂参数，在光学软件Lighttools中进行建模分析，如图4(a)所示。无论如何转动漫反射镜的角度，只有近轴光线会经过漫反射镜反射后再次进入PSM，最终由CCD接收到返回像点。理想情况下所有元件都处于同一基准轴线上无偏心，这样返回像点将落在CCD靶面中心，而实际情况下PSM存在加工及装配偏心，导致返回像光斑不在靶面中心，而且弥散斑尺寸较大且分布较离散，如图4(b)所示。因此，需要一种高精度方法确定光斑的质心位置坐标。

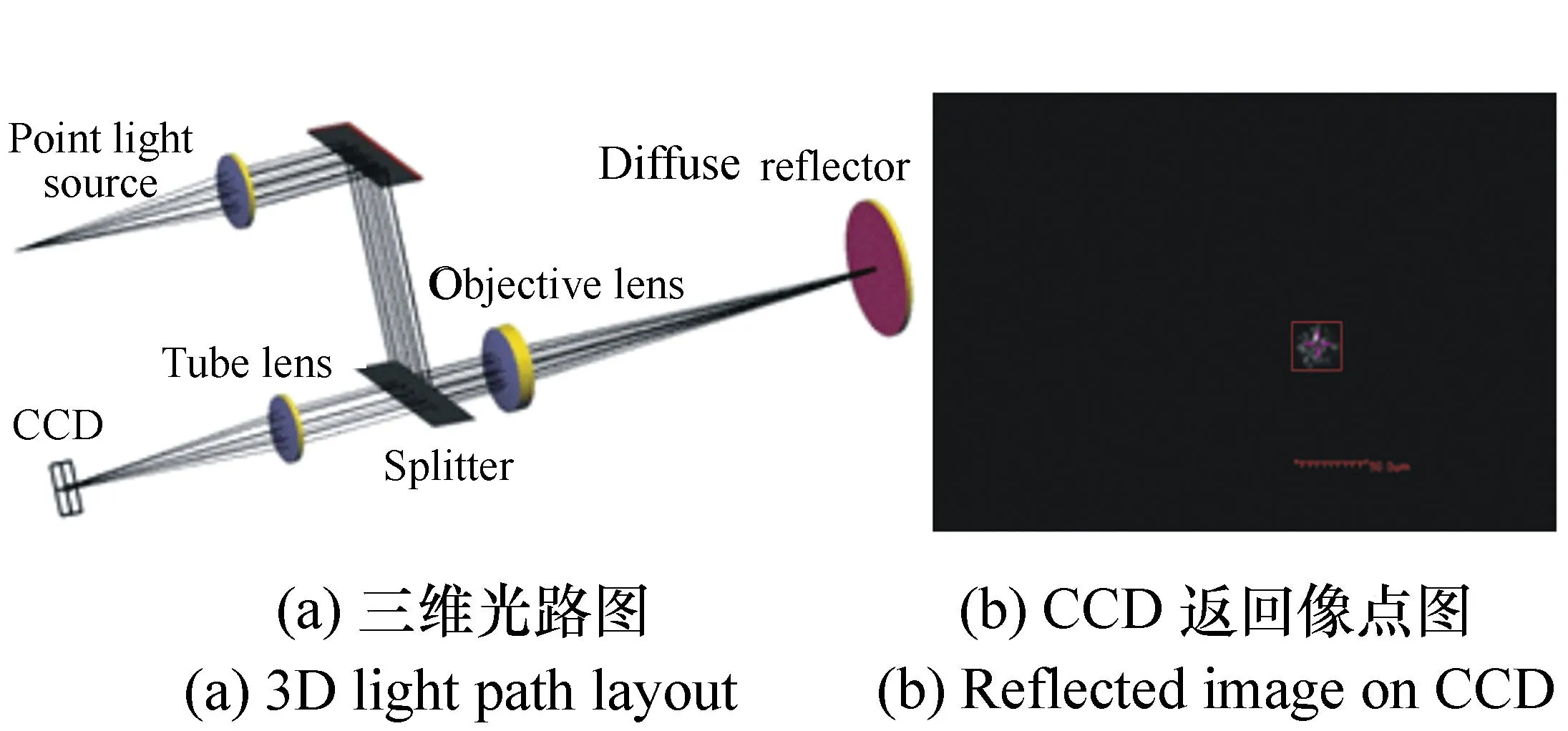
图4 基准零位仿真及实际返回像点图 Fig.4 Diagram of reference zero position simulation and real reflected image

通常情况下，理想的光斑质心坐标是探测器所对应区域S内对各个点的光强与坐标乘积的连续积分与光强在此区域内的积分比值，可表示为：

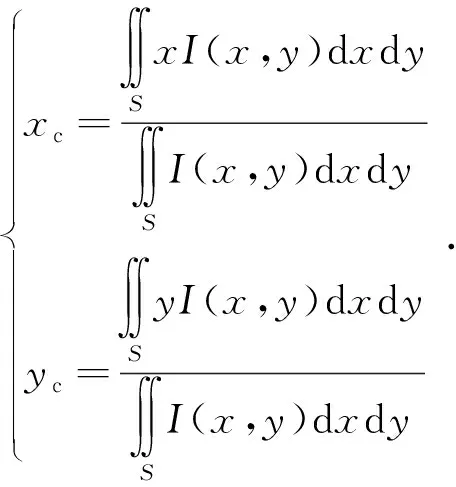
(1)

而CCD探测信号的总误差可表示为：

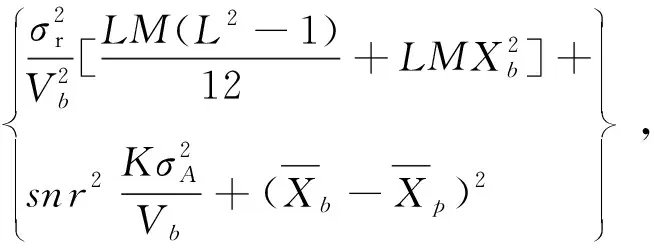
(2)

(3)

其中，M，N分别为探测窗口内图像行和列的像素数，xi,yj分别为对应像素点的横纵坐标，I为对应像素点的强度值，ω为加权函数，此处采用幂指数加权质心算法，其加权函数为ω=I3。同时将探测窗口选取与加权质心算法组合起来最大程度地提高质心探测精度，具体实现过程为：选取光斑尺寸稍大(1个像素)的模板，将模板置于光斑图像的左上角，按左上-右上-右下-左下的方式依次扫描并求取模板覆盖下光斑各像素强度和，将强度最大的模板位置作为实际光斑质心的探测窗口位置，利用该方法可将质心探测精度提升到亚微米级的0.15 pixel[14]，最终返回像光斑的质心如图4(b)矩形探测窗口内十字位置，该标注点即作为PSM的基准零位。

3.2 对准误差的求取

确定PSM的基准参考零位后，需要计算经同心物镜反射后像点质心位置与子眼安装孔轴线对准误差的几何关系式。如图5所示，图中样品为三胶合同心物镜的第一片透镜，由于同心物镜是各光学表面共心的球形透镜，若存在偏心量a，同心物镜球心位置偏离光轴a，可等效为物镜发生α角度倾斜，此时，返回光线将偏转2α，经物镜、分束器和管透镜成像在CCD靶面，设返回像点质心偏离基准零位的距离为d。

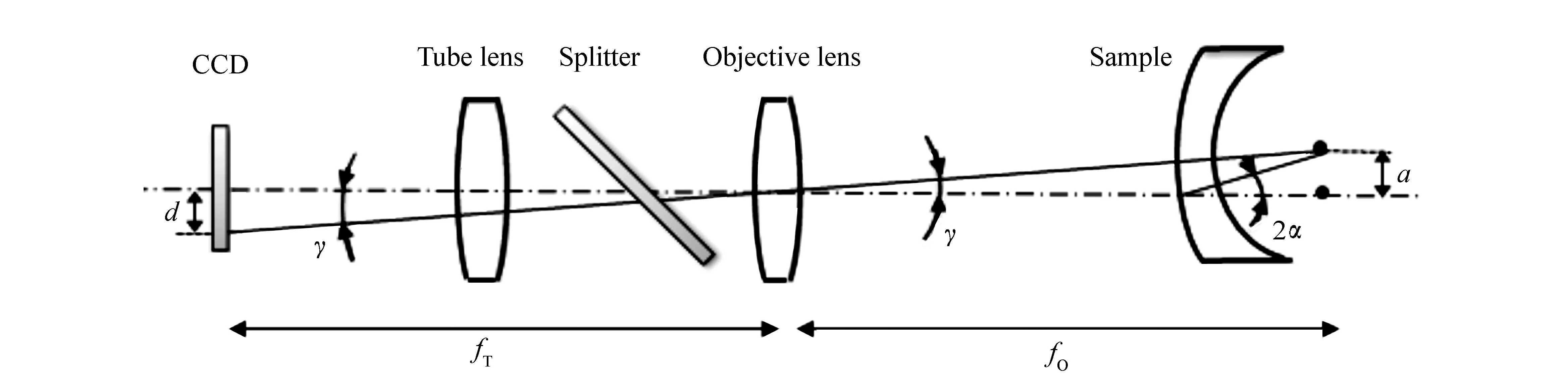
图5 子眼镜头安装孔对准误差与返回像点偏离量关系图 Fig.5 Diagram of relationship between alignment error of sub-eye mounting holes and deviation of reflected image

则有如下关系式：

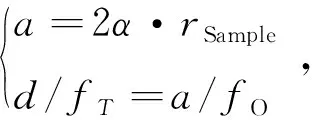
(4)

其中，fT为管透镜的有效焦距，由PSM出厂参数表给出，fO为物镜的有效焦距，rSample为同心物镜第一光学表面的曲率半径。利用 Lighttools对检测光路进行如图6(a)所示的模型建立。图6(b)为点光源发出光线经同心物镜第一表面反射后在CCD像面处接收的返回像点图。在对准误差检测过程中，PSM点光源发出的光线经同心物镜的第三、四胶合表面并反射后，返回像点能量很微弱，实际观测中返回像点只受第一、二胶合表面的影响，而第一、二胶合表面的偏心量可用定心仪控制在探测器的两个像元内，对子眼安装孔与同心物镜球心对准误差的影响基本可忽略。根据多次偏心量仿真结果，拟合出返回像点偏离量d与同心物镜球心偏离量a的函数曲线，如图6(c)所示，仿真结果与理论推导一致，因此可用式(4)进行所有子眼安装孔对准误差的检测实验。

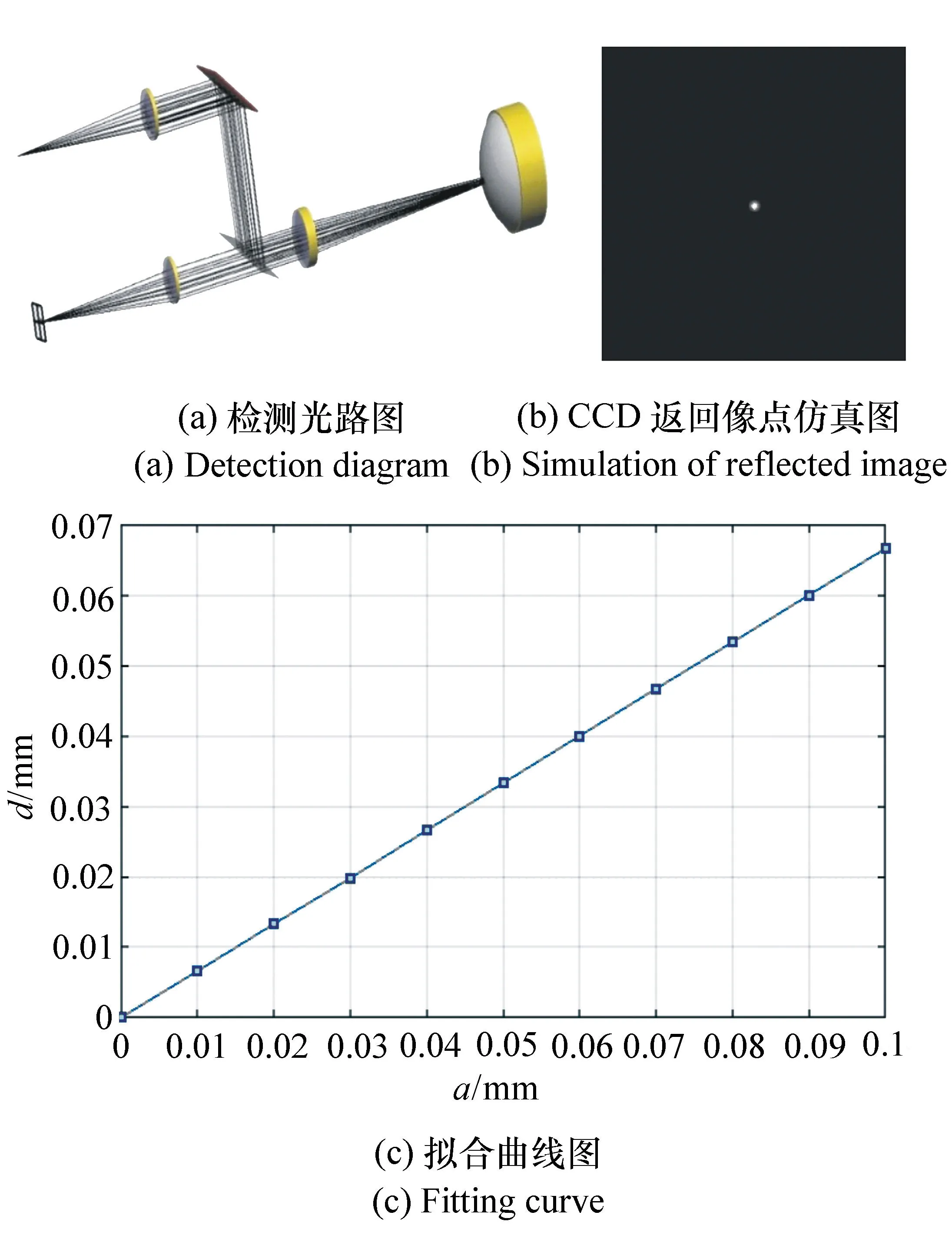
图6 检测光路建模仿真分析 Fig.6 Simulated analysis of detection model

4 检测实验与结果

采用上述仿真分析结果进行子眼安装孔轴线与同心物镜球心的对准误差检测实验，如图7(a)所示。实验选择穹顶奇数行的所有1-18号子眼镜头安装孔为样本进行检测。首先通过转接器将PSM分别固定在子眼安装孔中，理想情况下，转接器的外径与安装孔的内径完全一致以保证配合的紧密性。但在实际加工和检测过程中，间隙配合的安装方式必然导致在某些孔位置存在松动情况。仿生复眼系统的穹顶安装孔、转接器以及子眼镜筒均采用同型号德国哈默高精度五轴机床加工。这能够将子眼安装孔与转接器，以及子眼安装孔与子眼镜筒的安装配合误差通过间隙配合方式控制在5 μm范围内，设备的加工精度可保证子眼镜筒与转接器在安装时具有可互换性，对准误差的衡量只需在后期将加工精度引起的安装误差叠加到实际检测结果中，即可用转接器与子眼安装孔轴线的对准误差替代子眼镜筒与安装孔轴线的定位误差。由于支撑穹顶厚度为30 mm，根据式(4)可计算出安装孔与转接器，以及安装孔与子眼镜筒配合误差引起的对准误差最大偏离量为6 μm，并将其叠加至后续的检测结果中以评价最终对准误差。为获取更精确的检测结果，对于每个孔位置均进行多次测量，实验过程中将转接器分别绕安装孔轴线旋转，并采集10组数据取平均值，然后利用式(3)的加权质心算法求取CCD返回像点的质心坐标，并计算与PSM基准零位的距离d，最后再利用式(4)获取每个安装孔轴线与同心物镜球心的对准误差a。

图7 子眼镜头安装孔对准误差检测实验 Fig.7 Alignment error detection experiment of sub-eye mounting holes

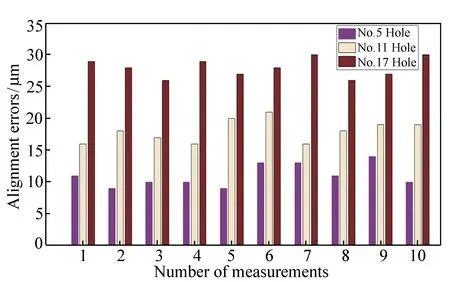
图8 5、11、17号安装孔对准误差多次检测结果 Fig.8 Detection results of alignment error for NO.5、11、17 mounting holes

考虑到子眼安装孔与转接器的配合误差，第 5、11、17号安装孔的最终检测结果如图8所示，其中横坐标表示测量次数，对每个安装孔均进行10次检测，纵坐标表示对应安装孔轴线与同心物镜球心的对准误差值。

所有18个安装孔位置的最终对准误差检测结果如图9所示，其中横坐标表示安装孔编号，纵坐标表示对应安装孔轴线与同心物镜球心对准误差的平均值。

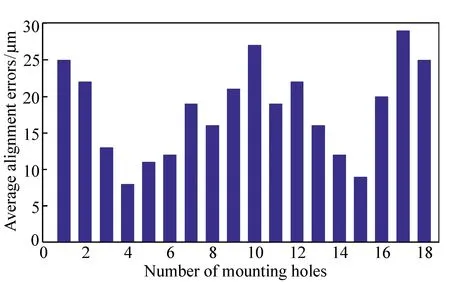
图9 18个安装孔位置对准误差平均检测结果 Fig.9 Detection results of average alignment error for 18 mounting holes

从检测数据可知，第 5、11、17号安装孔的对准误差平均值分别为11.2、17.9、28.1 μm，算术平均值标准差分别为0.68、0.66、0.62。由于每个安装孔的检测次数较少，为衡量检测数据的可信程度，按t分布计算极限误差[15]：

δlimx=±tσ,

(5)

其中，δlimx为极限误差，t为置信系数，σx为算数平均值标准差，根据t分布表，当置信概率为0.99时，每个样本安装孔分别进行10次测量，t=3.25，此时3个安装孔的极限误差分别为±2.21、±2.15、±2.02，所有检测数据与平均值的偏离量均在极限误差范围内，保证了检测结果的可靠性。参照图9可知，所有子眼安装孔轴线与同心物镜球心的对准误差均小于30 μm。上述结果表明，利用此对准方法可实现仿生复眼成像系统的子眼装调和标定工作，并获取了三亿像素无缝拼接图像，如图10(a)所示，其中(b)、(c)为500 m处目标的不同等级放大图像。

5 结 论

由于仿生复眼成像系统的结构特异性，传统检测方法难以快速准确地衡量各子眼镜头安装孔轴线与同心物镜球心的对准误差，从而无法严格保证全视场无缝拼接图像的获取。本文基于PSM定位仪的自准直反射原理，通过确定PSM的基准参考零位，推导经同心物镜反射的像点质心偏离量与子眼安装孔轴线对准误差的关系，建立了检测光路的Lighttools仿真模型，可精确衡量所有安装孔轴线与同心物镜球心的对准情况。该检测方法简单实用，适用于大尺寸复杂多孔类结构的轴线对准误差检测。实验结果表明，所有子眼安装孔轴线与同心物镜球心的对准误差均小于30 μm，即便考虑同心物镜的胶合偏心、PSM转接器与子眼镜筒的不一致性引起的微小影响，测量结果也完全满足光学设计中子眼镜头光轴与同心物镜球心对准误差小于50 μm的公差要求，从而保证了仿生复眼成像系统大视场高分辨率无缝拼接图像的获取。