数学化归法的运用——以“函数与角度”为例

☉湖北省武汉市二桥中学 张 蓓

有这样一个故事，一天，数学家波利亚碰到一个物理学家，他问这个物理学家：“给你一个煤气灶，一个水龙头，一个空水壶，让你烧一满壶开水，你应该怎么做？”物理学家回答：“把空水壶放到水龙头下，打开水笼头，灌满一壶水，再把水壶放到煤气灶上，点燃煤气灶，把一满壶水烧开.”

波利亚说：“对，这个问题解决得很好.现在再问你一个问题：给你一个煤气灶，一个水龙头，一个已装了半壶水的水壶，让你烧一满壶开水，你又应该怎么做？”物理学家说：“把装了半壶水的壶放到水笼头下，打开水龙头，灌成一满壶水，再把水壶放到煤气灶上，点燃煤气灶，把一满壶水烧开.”但是波利亚的回答是：“把装了半壶水的水壶倒空，就化归为刚才已解决的问题了.”

化归的数学方法是在研究和解决有关数学问题时，采用某种手段，将问题转化，进而得到解决的一种方法，一般将问题由难化易，由简化繁，由复杂化简单.下面就以武汉市中考第24题为例，针对函数与角度问题，运用数学化归思想解决这类问题.

一、课堂前置

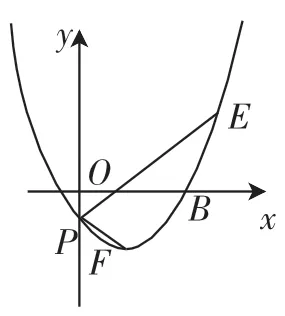
图1

选择学生比较熟悉的四个函数与角度的问题，让学生自己动手解决，并尝试发现四个题目的内在联系.

题目1：如图1，抛物线y=x2-2x-1交y轴于点P，且经过点E（3，2），点F为抛物线上一点，且PF⊥PE，求点F的坐标.

解题过程：过点E、F分别向y轴作垂线，交y轴于M、N两点.

由PF⊥PE，得∠EPF=90°.易得△EMP △PNF.

则-1-a=a2-2a-1，则a1=1，a2=0（舍去）.

则点F（1，-2）.

思考：学生利用垂直这个条件，得到两个角互余的相似直角三角形，从而得到线段关系，进而转化成点的坐标，最后求出结果.

题目2：如图2，抛物线y=x2-4x+3交x轴于A、B两点，与y轴交于点C，连接AC，点P为第一象限内抛物线上一点，且∠ACP=45°，求点P的坐标.

解题过程：过点A作AM⊥AC交CP于点M，过点M作MN⊥x轴，交x轴于点N.

思考：这一题与上一题有什么区别呢？没有垂直的条件，所以要把这个问题转化成上个垂直的问题，因此，过点A作AM⊥AC，通过构造，就将此问题化归为第一个数学问题了.

下面，我们再来看第三题（武汉市中考第24题），方法是不是就很明显了呢？

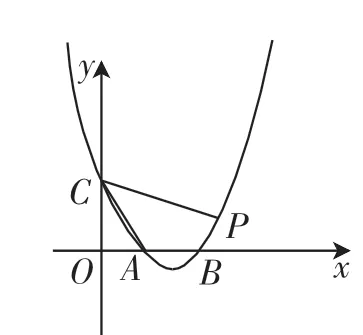
图2

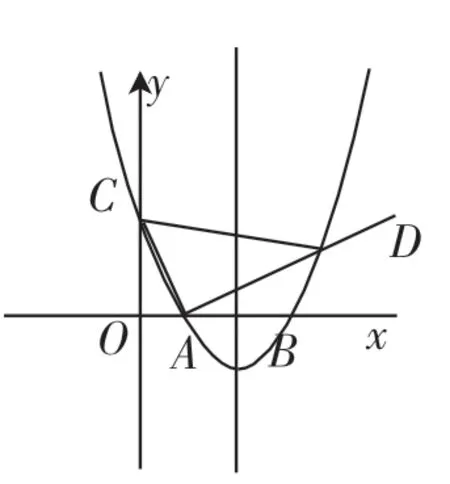
图3

题目3：如图3，已知抛物线与x轴交于A、B两点，与y轴交于点C.P为抛物线的对称轴上的动点，且在x轴的上方，直线AP与抛物线交于另一点D，连接AC、DC，若∠ACD=60°，求点D的横坐标.

解题过程：（化归为第一个数学问题）过点A作AM⊥AC，交CD的延长线于点M，过点M作MN⊥x轴于点N.

最后来看：这个问题是否也能化归为第一个数学问题呢？请主动尝试一下.

题目4：如图4，已知抛物线与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，连接AC、BC，点P是第一象限内抛物线上一点，连接PC，tan∠PCB=3，求点P的坐标.

解题过程：过点B作BM⊥CB交CP的延长线于点M，过点M作MN⊥x轴交x轴于点N.

直线CM的解析式为y=x+2.

则点P（7，9）.

那么，是不是所有函数与角度问题都可以化归为第一个数学问题呢？我们继续往下看.

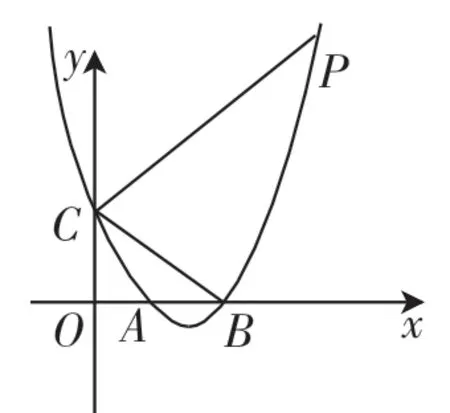
图4

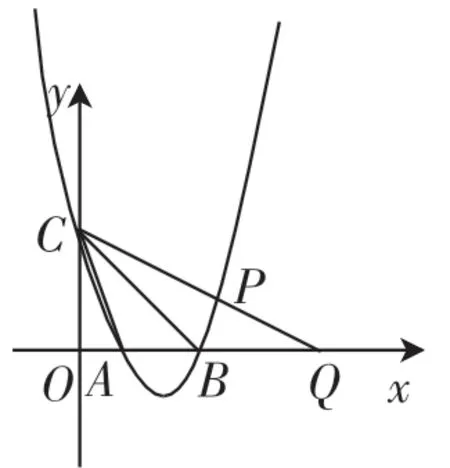
图5

题目5：如图5，已知抛物线y=x2-4x+3与x轴交于A、B两点，与y轴交于点C，连接AC，过点C作直线交抛物线于点P，交x轴于点Q，且∠PCB=∠OCA，求点P的坐标.

这题的解法有多种，可化归为第一个数学问题解决.

方法1：过点B作BM⊥CB交CQ于点M，过点M作MN⊥x轴于点N（化归为第一个数学问题），得到两个相似的直角三角形，从而得到线段比，进而求出点的坐标.最后通过直线与抛物线的解析式，求出交点的坐标.

方法2：过点A作AM⊥CA交CQ于点M，过点M作MN⊥x轴于点N，（化归为第一个数学问题）得到两个相似的直角三角形，从而得到线段比，进而求出点的坐标.最后通过直线与抛物线的解析式，求出交点的坐标.

总结：函数与已知角（特殊角度、已知三角函数值的角度、可求三角函数值的角度等）的问题都可化归为第一个数学问题，从而解决问题.

那么，如果是函数与未知角，又该如何解决呢？我们一起来看看.

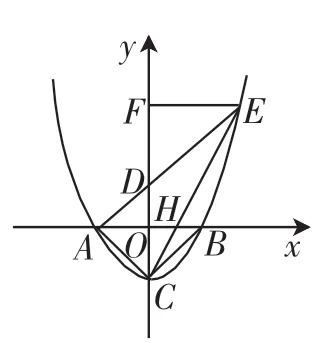
图6

题目6：如图6，抛物线y=x2-n2（n＞0）与x轴交于A、B两点，交y轴于点C.

（1）当∠ACB=90°时，求抛物线的解析式；

（2）E为第一象限内抛物线上一点，连接AE、CE，AE交y轴于点D，CE交x轴于点H，过点E作EF⊥y轴于点F，若∠EAO=∠ECO，求DF的长.

分析：这个问题显然不能化归为第一个数学问题，我们可以创造一个新的模型解决这一类动角（未知角）问题.

∠EAO=∠ECO，找这两个角所在的三角形（直角三角形），由相似得到线段关系，进而得到点的坐标，从而解决这类问题.

图7

通过以上总结，你可以自己来解决函数与角度问题了吗？其实，只需要区分角度是哪一类，我们就可以用化归法将问题转化，从而解决好函数与角度问题.下面我们来检测一下吧.

［素养提升］

练习题1：抛物线y=-x2+bx+c与x轴交于A、B两点（点A在点B的左边），与y轴的正半轴交于点C.

（1）如图8，若点A（-1，0）、B（3，0），

①求抛物线的解析式；

②P为抛物线上一点，连接AC、PC，若∠PCO=3∠ACO，求点P的横坐标.

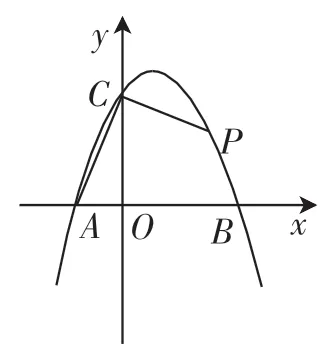
图8

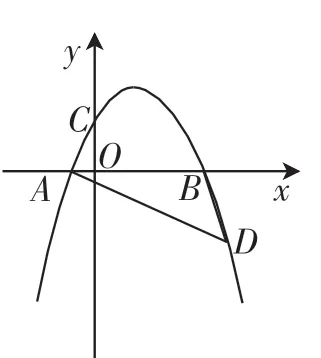
图9

（2）如图9，D为x轴下方抛物线上一点，连接DA、DB，若∠BDA+2∠BAD=90°，求点D的纵坐标.