海上搜救辅助决策技术研究进展

朱 岿，牟 林，2，王道胜，2，孙均楷

（1.中国地质大学（武汉）海洋学院，湖北 武汉430074；2.中国地质大学深圳研究院，广东 深圳518057）

我国是一个拥有300万平方公里蓝色国土以及1.8万公里海岸线的海洋大国。2017年我国海洋生产总值77 611亿元，其中海洋交通运输业全年总值6 312亿元，比上年增长9.5%［1］。海上运输贸易持续发展的同时，海难事故的风险也日益增长。据中国海上搜救中心统计，2017年全国各级海上搜救中心共核实遇险事故2 053起，搜救遇险船舶1 081艘，搜救遇险人员14 983人。为了及时应对日益频繁的海难事故，保障人民生命和财产安全，国家相关部门对海上搜救工作给予了高度重视。海上搜救包含了搜寻和救助两个部分，而海上搜寻是进行海上救助工作的前提，也是搜救工作中最复杂、最关键的部分。近年来，我国专业搜救力量不断加强，救助能力不断提升，但是在搜寻过程中的决策规划仍然过多的依赖经验。为了避免行动组织的盲目性，提高海上搜救指挥和协调工作的效率和准确性，对海上搜救辅助决策关键技术进行研究至关重要。

海上搜救辅助决策的研究是为了辅助决策者在最短的时间内利用有限的搜寻资源制定搜寻方案以提高海上遇险目标搜寻工作的成功概率（Probability of Success，POS），而POS主要依赖于搜救区域包含搜寻目标的概率（Probability of Containing，POC）和目标在搜救区域中时能够被成功探测到的概率（Probability of Detection，POD）［2］。因此海上搜救辅助决策涉及到两个关键问题：一、海上搜救区域的最优确定，其本质是通过综合考虑并量化遇险目标漂移过程中的所有影响因素（遇险位置、目标类型、影响目标漂移的风场、浪场以及流场等）来计算目标漂移轨迹及其最终位置的概率分布，进而确定最优的搜救区域；二、海上搜寻方案的最优规划，即在搜救区域确定的基础上，寻求一种搜救资源在时间和空间上的最优分配方案以提高成功探测概率。本文从这两个问题入手，介绍了海上搜救辅助决策关键技术的相关研究：针对于问题一，讨论了遇险目标漂移模型的发展，分析了漂移轨迹和搜救区域的两种经典计算方法；针对于问题二，分别对静止和运动目标最优搜寻策略的研究进行了介绍。进而，总结了国内外相关的应用情况，探讨了相关技术未来的发展方向，以期对该领域研究人员有所裨益。

1 海上搜救区域的最优确定

遇险目标搜救区域的最优确定需要保证选取的区域尽可能包含搜寻目标（即包含概率POC接近于1），同时搜寻区域面积不能过大从而避免成功探测概率过低。该问题通常被分解为遇险目标漂移建模和建立在其基础上的漂移轨迹及搜救区域计算建模。前者从遇险目标海上漂移的动力机制出发研究其运动特征和驱动力的关系，后者以前者为基础，着重从迭代计算和误差分析的角度通过求解运动轨迹方程来确定搜救区域。

1.1 海上遇险目标漂移模型

海上遇险目标漂移模型的研究可以追溯到1944年。之后，众多学者针对海上遇险目标的漂移运动进行了实验，试图构建遇险目标的运动和海洋环境动力的关系模型。根据Anderson等（1998）对海面漂移物体的运动受力分析［3］，遇险目标在海上漂移的过程中，水下部分主要受到表层流和波浪的影响，而水上部分主要受到风的影响。因此，海上遇险目标漂移速度V→可以近似表达为：

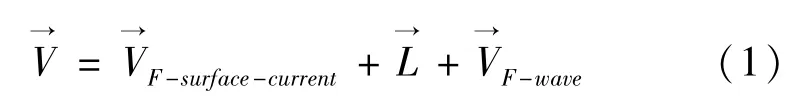
以下对流、海面风和波浪对海上遇险目标漂移运动影响的相关研究进行概述。

1.1.1 流致漂移模型 流可以分解为密度流、风生流、潮流等几部分。其中海水表层部分在水平方向上的运动对海上遇险目标漂移的影响占据了主要部分。流致漂移速度可用下式表示：

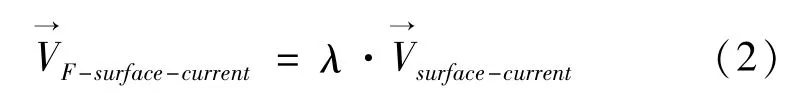
一般模型对流致漂移的处理较为简单，认为流致漂移速度近似等于海水表层流速［3］，而众多实验［4-5］也从侧面证明了流致漂移系数λ近似为1.0。

1.1.2 风致漂移模型 Hodgins等（1995）提出风致漂移（LEEWAY）的定义［6］：由于风作用于物体的水上部分而导致其相对于周围海流的运动。Allen等（1999）首次基于大量海上实验的结果建立了定量化的LEEWAY模型［7］，认为对于大多数搜救目标（长度小于海浪波长），波浪作用力可以忽略，并对LEEWAY进行了严格的定义：LEEWAY是指由于海面风（10 m高）和表面流（0.3～1.0 m深）引起的物体漂移运动。模型以风速和风致偏移角为参数（图1）为进行海上实验的63类搜救目标建立了风致漂移方程。

早期的LEEWAY模型在风速较小时无法准确的解释风致偏移角的波动性。Allen（2005）将风致漂移速度分解了为更具鲁棒性的沿风向速度（DWL）和侧风向速度（CWL）两个分量［8］（图1），重新建立了风致漂移方程（式3）。其中，侧风向速度CWL左偏（-CWL）和右偏（+CWL）的概率相同。

图1 LEEWAY模型风致漂移速度分解示意Fig.1 Schematic diagram for the decomposition of wind induced velocity in LEEWAY model

LEEWAY模型：

式（3）中：L为风致漂移速度，a、b为拟合系数，ε为拟合标准差，下角标d，c+，c-分别对应顺风、右偏、左偏风向；W10为海面10 m高度风速，Lα为风致偏移角。

改进的LEEWAY模型为海上遇险目标的漂移预测研究提供了更为精确的理论基础，目前已经被应用至挪威［9］、美国［10］、葡萄牙［11］等多个国家的海上搜救系统中。国内外众多学者基于LEEWAY模型对不同类型的搜救目标进行了风漂系数率定和应用研究工作。

Allen等（2010）和Breivik等（2012）基于LEEWAY模型针对不同体积的漂移物体提出了直接和间接观测的实验方案［12-13］，对油桶、二战时期LMK2水雷和落水集装箱等多类目标进行了现场实验，并研究了不同载荷比下落水集装箱的风漂系数。

Brushett等（2014）率定了太平洋岛屿群落常见的3种小型船舶的顺风和侧风向风漂系数并且针对不同载荷下划艇（5.8 m）进行多组实验［14］，实验结果表明划艇在载荷1～13人范围内，风漂系数介于7.71%～4.40%之间。

徐强强等（2017）基于实测资料利用谱投影梯度法对海上搜救目标的风漂系数进行了优化实验［15］。陈海涛等（2017）基于东方红2号船漂移实测数据利用最小二乘法拟合得到了船舶顺风和侧风向风漂系数［16］。此外，旷芳芳等（2017）、黄娟等（2014）也对落水人员等遇险目标进行了风致漂移的研究［17-18］。

1.1.3 浪致漂移模型 波浪对遇险目标运动影响的作用机制比较复杂，其对漂移物体的影响主要通过波浪的直接作用力和风生波浪引起的Stokes漂移。由于风生波浪引起的Stokes漂移作用主要集中在水体表层且不易从风漂速度中分离，因此其影响通常被假定存在于经验风漂系数中而不再考虑［11］。而波浪直接作用力对物体运动的影响则与物体尺寸相关，通常认为对于多数遇险目标（长度小于30 m），波浪作用力的影响可以忽略不计［10］。

Tanizawa等（2009）的实验研究表明由波浪驱动的目标漂移速度大小与波长及目标尺寸相关［19］。胡志武等（2007）推导并建立了由波浪引起的漂流速度的表达式［20］，具体为：

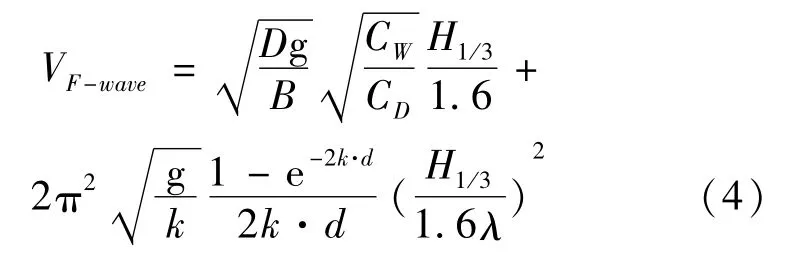
式（4）中：D为目标尺寸，B为目标水下的投影面，CD为流体阻力系数，CW为波浪漂流力的作用系数，H1/3为有效波高，d为目标吃水深度，λ和k为波长和波数，g为重力加速度。

在前人的研究基础上，Röhrs等（2012）通过在动量方程中加入科里奥利力和Stokes效应来分别研究了考虑和去除LEEWAY作用下Stokes漂移对目标运动的直接影响［21］。徐江玲等（2017）和刘同木等（2017）基于海上实验分别研究了浪致漂移对大型浮标和落水人员的漂移运动影响［22-23］，结果表明考虑浪致漂移能够在一定程度上提高漂移轨迹预测精度。

1.2 漂移轨迹及搜救区域计算模型

在漂移模型的基础上，理论上只要给定了遇险目标的类型、风场、浪场和流场等足够的信息即可计算任意目标的运动轨迹：

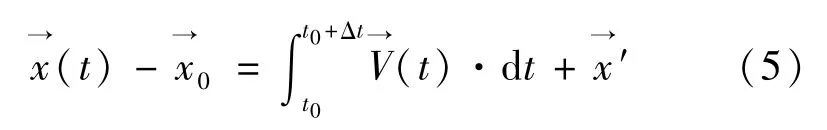
实际上，由于真实目标物的几何结构是不规则的，动力场也存在误差，计算净运动十分困难，因此搜救区域的计算需要对各项误差进行简化或仿真模拟。搜救区域计算模型主要分为两类：解析法和蒙特卡洛法。

1.2.1 基于解析法的搜救区域计算模型 解析法模型发展较早，早期模型以手动解析计算为主，1970年前后手动计算开始逐渐被计算机取代。1999年，国际海事组织和国际民用航空组织联合出版了《国际航空和海上搜寻救助手册》［24］，手册统一和规范了各国航空和海上搜救规划的解析方法。解析法将目标物的失事位置作为模型起算点，利用建立的漂移模型将风和流致漂移的矢量进行迭加以计算各时刻目标的位移。模型中的搜寻范围由搜寻基准区域和误差区域相叠加得来，如图2所示。

图2 解析法搜寻基准区域示意Fig.2 Schematic diagram of reference area by analytical method

搜寻的基准区域为椭圆形式，其长轴与风向平行，长短半轴的长度为时间的函数：

式（6～7）中：R1和R2分别表示椭圆长短半轴的长度，Lα表示风致偏移角，V风表示风速，Δ风向、Δ风速表示风向和风速误差，B表示载荷情况误差。

《国际航空和海上搜寻救助手册》中推导了遇险目标在搜寻区域中关于长、短半轴的概率密度分布函数［24］。Burciu等（2002）采用Fokker-Planck方程对基准区域中遇险目标的概率分布情况进行了作图［25］，将该概率分布做成了概率椭圆。

解析法尽管在一定程度上建立出了目标漂移运动与海流、风等相关影响因素的关系模型，但由于其只是模拟了基于基准点的一条或者几条漂移轨迹，对于目标漂移运动过程中产生的所有随机误差的估计只能通过扩大概率椭圆半径的方式来进行模拟，以致最后计算的搜救区域面积往往过大而降低了成功探测概率。

1.2.2 基于蒙特卡洛法的搜救区域计算模型 早期的搜救辅助决策系统多数基于解析法。21世纪以来，以SARMAP、SARIS等为代表的经典搜救辅助决策系统都在各自的系统中添加了基于蒙特卡洛法的搜救区域计算模块，以期提高系统预测精度。

①蒙特卡洛法基本介绍 蒙特卡洛法又称统计模拟方法，是在20世纪中期由于电子计算机发明而被提出的一类非常重要的数值计算方法［26］。1972年，美国海岸警卫队首次将蒙特卡洛法应用至搜救作业系统CASP中［27］。蒙特卡洛法把目标抽象成一组相互独立的粒子集合，根据建立的漂移模型，由漂移速度来估算各粒子的运动轨迹。粒子在海面上的漂移运动满足马尔科夫过程，因此粒子集未来所处位置的概率密度函数仅仅依赖于海洋环境状态［9］：

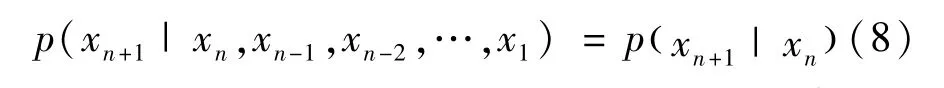
式（8）中：xi（i=1，2，3，…，n，…）表示第i时刻目标的位置，p表示条件概率。单个粒子的随机漂移过程可表示为：

式（9）中：d x为粒子单位时间内的位移，V为风、浪、流共同作用下的粒子漂移速度函数，dε为随机扰动项，表示风漂属性、海洋环境动力数据等存在的误差。

相比解析法，蒙特卡洛法运用了统计学的方法，通过引入粒子仿真法能够模拟目标漂移计算过程中所有不确定因素，同时能够有效的结合逐渐丰富且精确的海洋环境动力数据。此外当模型进行数值计算时，可以使用分布式运算使模拟过程分布独立进行，能够快速获取结果。肖方兵等（2011）利用美国弗罗里达州大西洋大学的落水人员漂移实验数据分别采用解析法和蒙特卡洛法对目标进行了搜救范围预测［28］，结果证明蒙特卡洛法能够大幅降低预测区域面积，并能准确的吻合目标漂移轨迹。

②基于蒙特卡洛法模型的研究 蒙特卡洛法模型通过扰动相关系数、驱动场和粒子初始分布，多次运行漂移轨迹预测模型进行拉格朗日粒子追踪来产生一系列集合，进而获取搜救区域的概率密度分布。风漂系数以及粒子初始分布的扰动相对简单，《国际航空和海上搜寻救助手册》［24］概述了几种基于参考点、线和区域的遇险场景来建立初始粒子概率分布的方法。Gao等（2018）蒙特卡洛法在疑似遇难海域设置了3组不同初始时刻均匀分布的粒子对马航MH370航班的残骸进行漂移轨迹预测［29］。Breivik等（2011）基于非约束性的LEEWAY模型对回归方程中的风漂系数添加了服从正态分布的不同量级的扰动项［9］。郑宏喆等（2016）利用蒙特卡洛方法扰动风漂系数的同时考虑了风压差翻转，建立了搜救区域计算模型并进行了仿真实验［30］，结果表明代入风压差翻转率的计算方法可以在一定程度上提高模型精度。

随着海洋数值模型发展，基于蒙特卡洛方法对于驱动场的扰动出现了不同方案。目前多数蒙特卡洛法模型采用的是确定性（单一模式）的海流、风矢量场配合随机走动系数［31］或者更复杂的二阶随机飞行模型［32］来实现驱动场中海流和风速的扰动。

而海洋模型集合的研究已经提供了一个利用矢量场集合来估算海上粒子扩散和漂移的可能性［33］。Melsom等（2012）基于TOPAZ海洋预报系统利用不同的初始场和扰动条件生成了100个模拟场集合［34］，实验比较了漂流示踪器在集合平均矢量场和确定性矢量场中加入随机飞行扰动的漂移模拟结果。然而实验结果表明，利用集合平均矢量场进行轨迹预测的结果并不优于在确定性矢量场中添加随机飞行扰动系数的方案。Rixen等（2007、2008）采用多模型集合建立了另一种海洋模型集合的方案［35-36］。Scott等（2012）集合了5个海洋模型对赤道大西洋区域分布的粒子进行了模拟并将计算加权平均值得到的轨迹和实测轨迹进行了对比［37］。实验结果表明多模型集合平均预测精度优于单个模型预测精度。Brushett等（2017）利用4个海洋模型的计算结果作为随机粒子漂移的环境强迫来预测小艇的漂移轨迹和搜救区域［38］，实验结果发现4个强迫场下计算得到的搜救区域的公共重叠区域面积约为单个模型平均搜救区域面积的三分之一，并且公共区域能较好的覆盖搜寻目标漂移轨迹。

2 海上搜寻方案的最优规划

海上搜寻方案的最优规划是在海上搜救区域确定的基础上，寻求一种搜救资源在时间和空间上的最优分配方式以提高成功探测概率（POD）。

搜寻理论属于运筹学研究的一个分支，它的研究主要起源于二战时期盟军应对德国潜水艇威胁的需要。Koopman（1946）公开了搜寻理论的第一份研究报告，总结了二战期间反潜战的研究成果，并建立了早期的搜寻模型［39］。二战后，搜寻理论得到了进一步发展。搜寻理论根据搜寻目标的状态分为静止目标搜寻和运动目标搜寻［40］。早期研究建立的搜寻模型将搜寻目标假设为静止状态，这类模型在实际海上搜救应用中的适用性有限；运动目标搜寻问题相对复杂，但更符合海上搜救工作的实际需求。

2.1 静止目标搜寻问题

静止目标搜寻问题通常伴随着两点假设（即搜寻目标的概率分布密度函数已知，并且搜寻资源在搜救区域无限可分）来规划理论最优搜寻方案，再通过近似方法构建可执行的搜寻资源分配方案来逼近理论最优搜寻方案。

Koopman（1956、1956、1957）相继发表了关于搜寻论的3篇论文［41-43］，首次提出了静止目标搜寻问题的基本理论。Koopman假定静止目标位置符合二元正态分布，探测函数为指数形式，在此基础上提出了横向距离曲线和扫视宽度等概念，建立了基于视觉发现的反立方律探测模型，并且提出了在目标连续的空间中、搜寻资源连续可分的情况下进行搜寻的最优资源分配方法。视觉反立方律探测模型中假设搜寻单元距离海面高度h探测搜寻目标尾迹，则某时刻发现目标的概率P与搜寻单位距离目标尾迹的平面距离r的立方成反比：

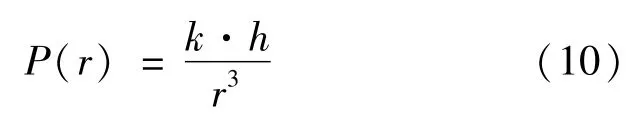
式（10）中：k为比例系数，与目标尾迹面积、目标性质和海况条件等相关。

对于符合反立方率的探测单位，使用有序平行线搜寻方式的发现概率和覆盖因子的关系为：

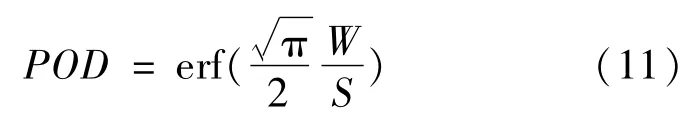
式（11）中：erf表示误差函数：

式（12）中：W表示扫视宽度，S为平行线搜寻的航线间距。

搜寻资源的最优分配模型可以表示为：

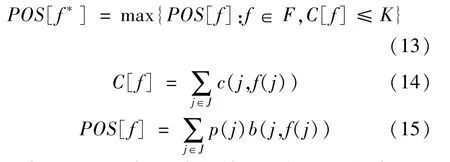
式（13～15）中：F表示搜寻空间J上的分配函数f：J→ ［0，∞）的集合，c（j，f（j））表示成本函数，K表示成本限额，p（j）b（j，f（j））表示目标位于单元j同时被搜索资源f（j）成功探测的概率。此时，分配f*即为对于成本K，在分配集合F中的最优分配方案。

Koopman的研究成果为搜寻理论的发展奠定了基础，然而他的搜寻理论仍然存在很多局限性，例如反立方规律的前提是在理想情况下目标在搜救区域内静止且随机均匀分布，并且搜寻单元沿直线以均匀速度进行搜寻。

之后，众多学者对搜寻理论进行了优化和改进。Charnes等（1958）将最优搜寻资源分配的问题转换为凸多边形规划问题进行了研究，并基于理论开发了算法获取搜寻资源的最优分配方案［44］。De Guenin（1961）在Koopman搜寻模型的基础上进一步研究了连续空间里包含正规探测函数的搜寻问题，并针对探测函数建立了约束条件［45］，De Guenin的研究使得成功搜索到目标的总概率能够达到最大。Stone（2006）通过研究一类具有可分离约束条件的极值问题的非线性泛函的最优解，解决了搜寻问题中“最优搜寻资源配置存在的充分必要条件”，研究了渐进式最优配置和整体最优配置的关系［46］。

2.2 运动目标搜寻问题

Stone（1975）首先将运动目标分成马尔可夫和有条件的确定性运动两类形式并进行了研究［47］，该研究改进了搜寻理论中的探测函数以适应任意离散时间的运动搜寻目标，利用拉格朗日乘子法将有条件约束的最优搜寻力量配置模型转换为无约束的最优搜寻力量分配问题。

之后，众多学者围绕着这两类性质的运动目标对最优搜寻进行了研究。有条件的确定性运动目标一般被简化为静止目标的搜寻问题进行求解［48］，Pollock（1970）对离散空间中两个格子的搜寻问题进行了研究［49］。

此外，运动目标搜寻问题根据搜寻目标能否主动响应搜寻工作的性质可以分为单向和双向搜寻。而在实际海上搜救工作中，多数搜寻目标无法有效对搜寻工作做出反应，因此单向搜寻是运动目标搜寻问题主要研究方向，它可以进一步细化为两类问题：最优搜寻密度和最优搜寻路径。

最优搜寻密度研究是针对搜寻资源的相对理想状态，即搜寻资源可以任意划分，且各时间、空间上的搜寻资源之间没有相互限制。Brown（1980）利用指数形式的探测函数针对离散空间、时间上作马尔可夫运动的目标最优搜寻问题提出了最优搜寻的充分必要条件，并设计了规划最优搜寻方案的迭代算法［50］。Brown的研究在运动目标探测算法上实现了一定的突破。Washburn（1983）在Brown的算法基础上进行了改进和推广，提出了“向前向后”搜寻算法［51］。

最优搜寻路径问题的研究适用于搜寻时段的资源配置对其后续时段的搜寻资源配置产生一定约束的情形，其目的是在约束条件下求解某时刻成功探测目标概率达到最大的搜寻算法。Trummel等（1986）把最优搜寻路径问题转化为了NP（Non-Deterministic Polynomial）完备性问题［52］。Ohsumi（1989）把海上搜寻目标的运动抽象为一个扩散过程［53］，利用指数形式的探测函数和最优随机控制理论的思想研究了连续时间及空间上的搜寻问题，把最优搜寻方案的问题转换为了对动态规划Hamilton-Jacobi-Bellman方程的求解问题。

3 国内外相关应用

国外对海上搜寻和救助问题的研究起步较早，以美国、英国等为代表的发达国家已经建立起了较为成熟的海上搜救辅助决策业务化系统。国内海上搜寻和救助的研究发展时间较短。近年来，罗永宏（2004）、于卫红等（2005）、肖方兵等（2013）对海上搜救辅助决策系统的功能、关键技术和系统框架进行了深入探究［54-56］。下文列举国内外具有代表性的模型应用。

SAROPS系统（搜救最优规划系统）由美国海岸警卫队开发［57］，采用了LEEWAY模型中率定的63类搜救目标的参数集，并使用一个环境数据服务器，从多个来源获取风和流场的预测数据。模型为多个搜索单元推荐搜索路径，最大限度地增加了从搜索增量中检测到目标的概率。系统结合ARCGIS技术，采用向导式的用户界面（图3），可以实现漂移动画的显示，并且能够结合算法优化成功概率（POS）。

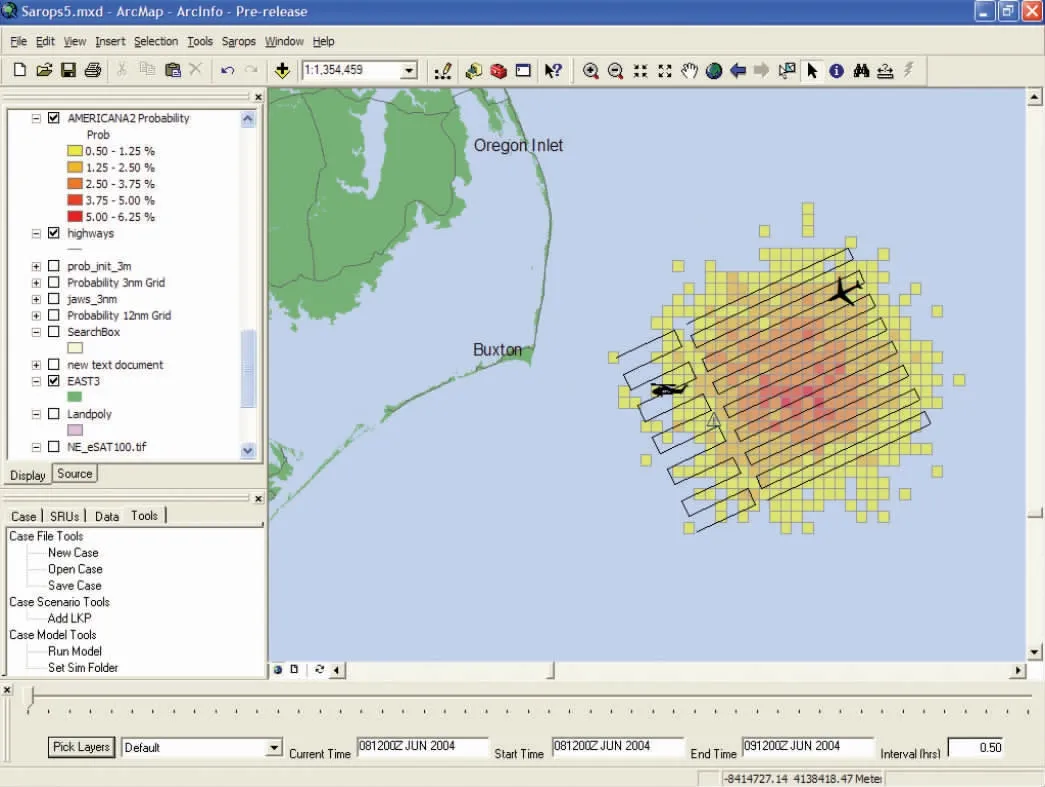
图3 SAROPS系统的操作界面Fig.3 Operation interface of SAROPS

英国BMT公司开发的SARIS搜救辅助决策系统（图4）应用广泛［58］。该系统可以使用解析法和蒙特卡洛方法来计算搜索区域，包含了搜救区域确定工具（SAD）和搜救区域覆盖工具（SAC）。SAD使用向导式的遇险位置推测和天气参数建模来确定最佳搜救区域，SAC集合了平行线搜寻、扇形搜寻和扩展方形搜寻等多种搜寻方式，采用UK CG3搜寻规划方法，是目前较为先进的海上搜救决策支持系统。

国家海上搜救环境保障服务平台（http：//marinesar.cn/，图5）由国家海洋局北海分局、东海分局、南海分局、国家海洋环境预报中心和国家海洋信息中心联合研制。该平台基于SOA架构和S57电子海图，集成了多模型和多环境数据源交互式专业预测、多用户协同预测、海洋环境预报场动态展示、数据下载、漂移预测简报制作、高频地波雷达观测同化数据集成、最优搜寻范围和搜寻计划智能规划等功能，不仅改进了现有的中国海和海区级海洋预报系统，还建设了针对12个海难事故易发区的精细化预报系统，实现了对中国海级、海区级和海难事故易发区的三级精细化数值预报系统优化，并投入了业务化运行。该平台系统的建设使我国海上搜救应急保障体系得到了全方位提升。

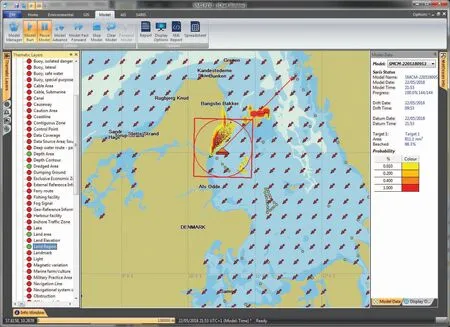
图4 SARIS系统的操作界面Fig.4 Operation interface of SARIS

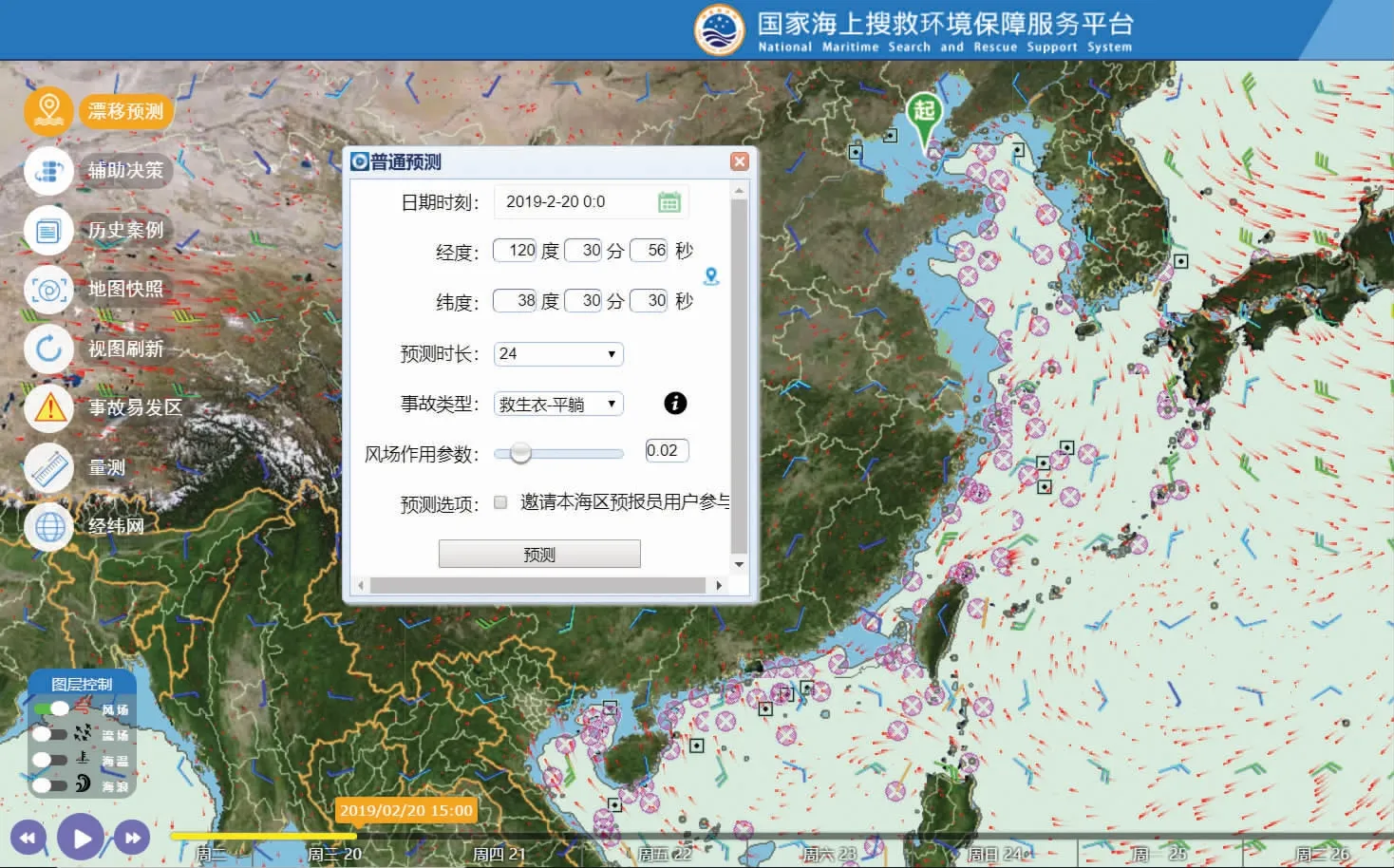
图5 海上搜救环境保障服务平台的操作界面Fig.5 Operation interface of National Maritime Search and Rescue Support System

4 总结和展望

本文总结了海上搜救辅助决策关键技术发展过程中的主要研究成果，从海上搜救区域的最优确定和海上搜寻方案的最优规划两个方面对海上搜救辅助决策关键技术进行了系统的介绍。在海上搜救区域的最优确定方面，基于对风、浪和流致漂移问题进行的研究，从解析法和蒙特卡洛法两类模型出发介绍了漂移轨迹及搜救区域的计算方法；在海上搜寻方案的最优规划方面，分别概述了运动和静止目标的最优搜索问题。最后，总结了国内外相关应用情况。笔者认为，海上搜救辅助决策技术的未来发展主要集中于以下几个方面：

（1）海洋模式的改进和多模型集合预报技术。局部高分辨率模型的研究可以提高中尺度特征和近海岸涡旋活动的模拟精度，而近海岸涡旋活动是大部分搜救作业所必需模拟的。同时多模型集合预报的方案也为进一步提高遇险目标漂移预测精度提供了可能。

（2）近岸高频地波雷达数据同化和预报技术。近岸地波雷达能够连续监测关注海域，因此基于高频雷达场的数据同化和短期（12～24 h）流场预报技术在近岸海上搜救工作中具有巨大的发展潜力［59］。

（3）风漂系数集的完善。海上遇险目标的风漂系数是一个相当重要的参数，目前广泛使用的风致漂移系数集主要由美国海岸警备队通过海上实验率定得到。此数据集质量各异，误差方差很大，各个国家需要结合自身区域特征的搜救目标重新进行实验。

（4）海上搜救单元搜救能力及适航条件评估。建立完善的搜救能力评估系统、科学制定各类搜救单元的适航条件等级评判集，是精确进行海上搜寻方案规划的前提。