关于四色猜想
2016-04-25沉潜
沉潜
中图分类号:O157.5 文献标识码:A 文章编号:1009-914X(2016)02-0374-01
证明:
【一】:在一个平面上最多只能有四个平面区域两两相邻。
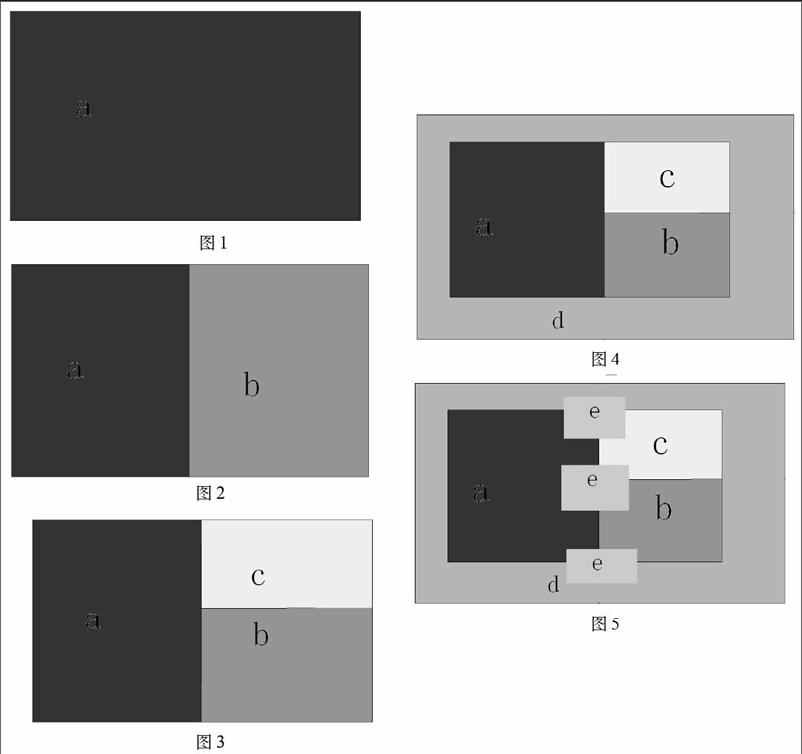
①在一个无限的连续的平面上,用一条直线将平面分割为两个区域,分别记为区域a、区域b。此时两个区域公共部分为一条直线。(见图1、图2)
②再用一条直线将两区域公共直线分割,直线同一侧的区域a区域b合为同一个区域c。此时三个区域公共部分为一个点。(见图3)
③由于点无法继续分割,要使第四个区域d与前三个区域都相邻,则需要第四个区域d将原三个区域包围。(见图4)
④此时四个区域已无公共部分,接下来要使第五个区域e 与前四个区域都相邻。先使区域e与三个区域相邻。而区域e无论与哪三个区域相邻,要与第四个区域衔接时都会被那三个区域阻挡。(见图5)
也就是说,在一个平面上最多只能有四个平面两两相邻,即四色猜想。
【二】:在一个空间上最多只能有五个立体区域两两相邻。
(个人能力有限,图略)
①在一个无限的连续的空间上,用一个无限平面将平面分割为两个区域,分别记为区域a、区域b。此时两个区域公共部分为一个平面。
②再用一个平面将两区域公共平面分割,平面同一侧的区域a区域b合为同一个区域c。此时三个区域公共部分为一条直线。
③继续用一个平面将三个区域公共直线分割,平面同一侧的区域a区域b区域c合为同一个区域d。此时四个区域公共部分为一个点。
③由于点无法继续分割,要使第五个区域e与前四个区域都相邻,则需要第五个区域e将原四个区域包围。
④此时五个区域已无公共部分,接下来要使第六个区域f与前五个区域都相邻。先使区域f与四个区域相邻。而区域e无论与哪四个区域相邻,要与第五个区域衔接时都会被那四个区域阻挡。
也就是说,在一个空间上最多只能有五个立体区域两两相邻。