电容角位移编码器电场仿真分析
2019-08-30崔小强曹国华丁红昌
崔小强,曹国华,丁红昌
(长春理工大学,长春 130022)
0 引言
容栅传感器是一种利用电容耦合作用,通过测量不同电容器上的电信号相位来精密测量位移的电子器 件[1]。对于传感器而言,无论是精度、分辨率、体积和成本都成为传感器在市场上竞争的热点。电容式角位移编码器具有较高的精度、分辨率和灵敏度,能够适应恶劣环境和实现非接触测量,并且低功耗、结构简单、对机械结构装调要求低等优点,广泛应用于各种需要测量角度的高精度平台[2,3]。但由于电容传感器存在量程小、输出阻抗高、存在寄生电容、抗干扰能力差、测量值受环境和外界电磁场的影响很大。国内外大多数学者对电容式角位移传感器从结构参数、电路设计等方面进行大量研究,尤其测量微小电容量的电路设计和敏感元件的设计[4,5]。
本文通过Ansys workbench和Ansoft maxwell软件对电容式角位移传感器进行有限元仿真分析,得到在不同情况下,电势的分布情况和电场强度分布情况。仿真不同结构参数的电容式角位移传感器,分析极板间的电容的变化、较为详细的模拟了电容式角位移传感器的工作情况,为后续研制更好鲁棒性能的高精度的电容式角位移传感器提供一些参考。
1 传感器结构选择
电容式角位移编码器主要由三个同轴且互相平行的极板组成,两个定板和一个动板组成,分布着发射电极和接收电极的为定板,固定在两侧,由覆铜的高精密印刷线路板构成。动板在两个定板之间,与外界轴相配合,其材料为高分子聚合物,具有较大的介电常数。其整体结构如图1所示。
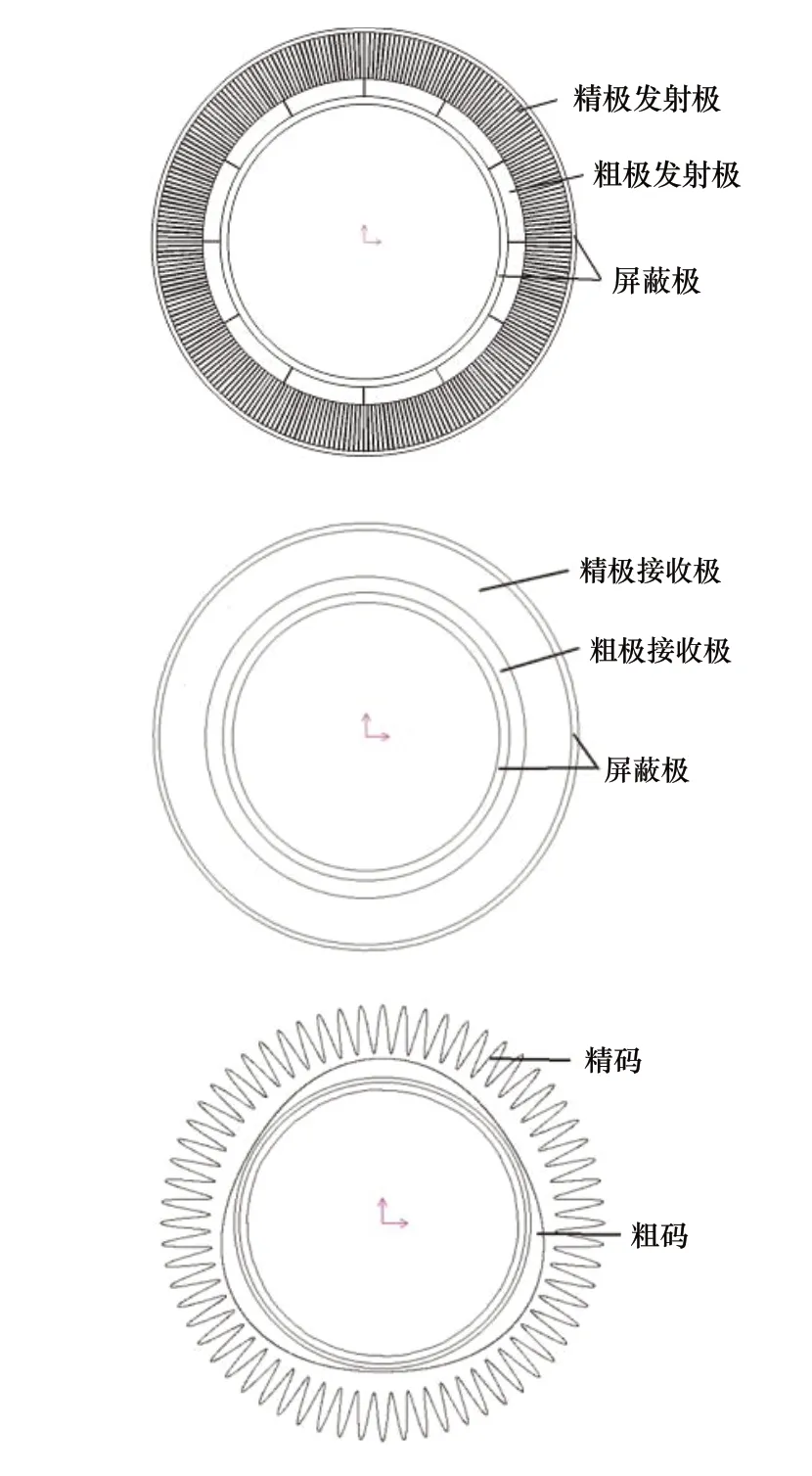
图1 传感器结构图
根据电容式角位移传感器的组成与工作原理,选定有限元分析的模型基本尺寸为:其基本尺寸为:极板外径φ1=84mm,孔径φ2=53mm,定板与动板之间间距d=0.2mm,动板厚度h=1.4mm。

图2 电容角位移传感器截面示意图
2 有限元分析
利用有限元分析的方法,求解电场、电压和电容值伴随着参数的变化的分布情况。
2.1 二维有限元分析
选用ansoft maxwell二维静电场有限元分析法,对传感器进行简化分析求解电势分布,截面图如图2所示。因此基于以下假设[6]:
1)传感器中电解质是各项同性,而且是均匀分布的。
2)介质的介电常数为恒定并且不依赖于电场。
2D有限元分析网格划分模型选用三角形单元,二维静电场具有对称性,场内的电势函数满足拉普拉斯变化,构造边界问题[7]:
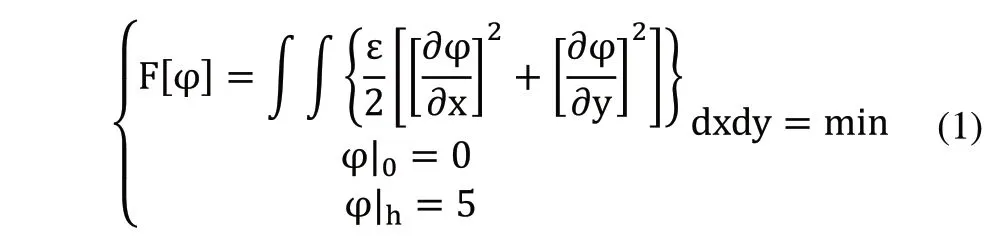

图3 三角形单元
将模型离散化,划分为有限个切互不重合的三角形单元,求得离散的电势方程:

式子中 为三角形单元顶点电位矩阵,

[K]e为三角形单元电场能系数。
2.2 三维有限元分析
3D有限元分析模型网格划分单元为最稳定的四面体单元,模型电场具有对称性,maxwell三维静电场边界条件较为简单,仅有Symmetry对称边界条件和 Master、Slave主从边界条件。场内的电势变化与二维模型类似,满足拉普拉斯方程构造三维电场电位边界 问题:

其边界条件为:
1)接收定板电位:0=0V
2)发射极板中施加电位:1=5V
其等价变分问题为:
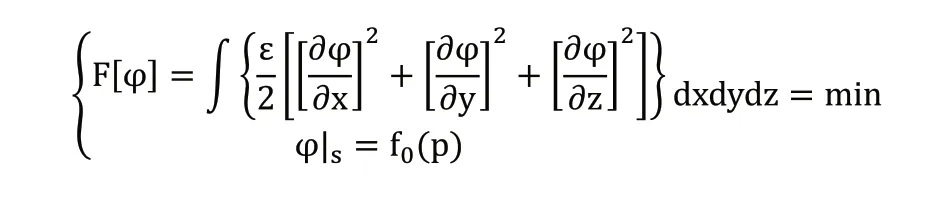
如图4所示,将三维场域剖分,剖分单元用四面体,变分问题离散化,则有矩形表示的电位离散表达式[8]:

图4 四面体单元结构
四面体是个顶点坐标为别为:(xI,yI,zI),(xJ,yJ,zJ),(xK,yK,zK),(xL,yL,zL)。四个顶点的场量通过四个顶点坐标表示。

经过矩阵变化可求出a,b,c,d,经过变量替换的方法得到:

基于ansoft maxwell和ANSYS有限元分析,对传感器2D和3D模型进行分析仿真得到电势分布和电容值随着传感器参数的变化产生的影响,对于边界条件的分析,选用气球边界条件来模拟绝缘系统,研究传感器内部电势分布和电容值的变化,选用Voltage,模拟静电接地系统。在发射极静板的发射极上施加5V电势,接收极的接收电势为0V。其模型如图5所示。

图5 仿真模型
3 仿真结果与分析
基于有限元分析,对电容传感器建模、有限元分析,得到2D、3D电势分布图和电场强度分布图,如图6和图7所示。
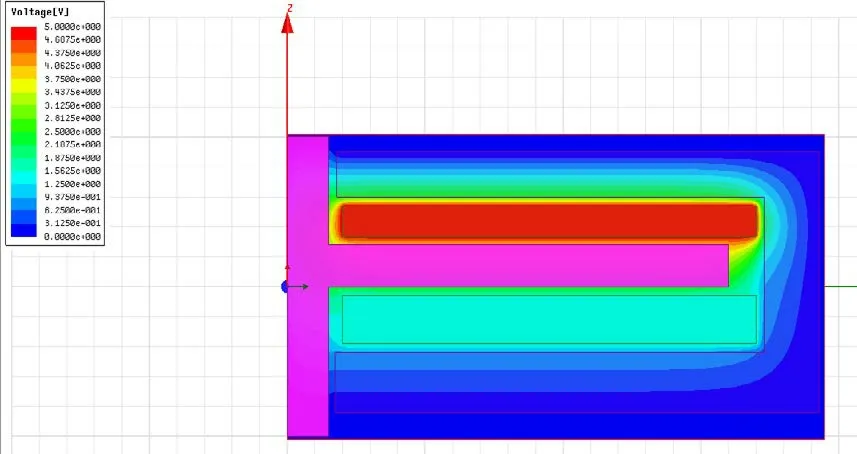
图6 二维电势分布图

图7 电势分布图
从图6和图7可看出,在接收极板电势分布比较弱,而且在极板边缘处电势分布和电场强度分布不均匀,电场的边缘效应对传感器输出信号有较大的影响。本文从改变板间间隙和屏蔽措施两个方面来研究其对电容式角位移传感器电势和电场的影响。
3.1 板间距的仿真研究
改变动板和静板之间的间距,只改变其单一变量,研究对传感器点式分布图的影响。由电容求解公式:

ε0真空介电常数
ε介质相对介电常数
A相对正对面积
d板间距离
由式(7)可知,当改变板间距离,电容值会发生变化,本实验当板间距在原来基础上从0mm扩大到0.2mm,来仿真电容值的变化。如图8所示。
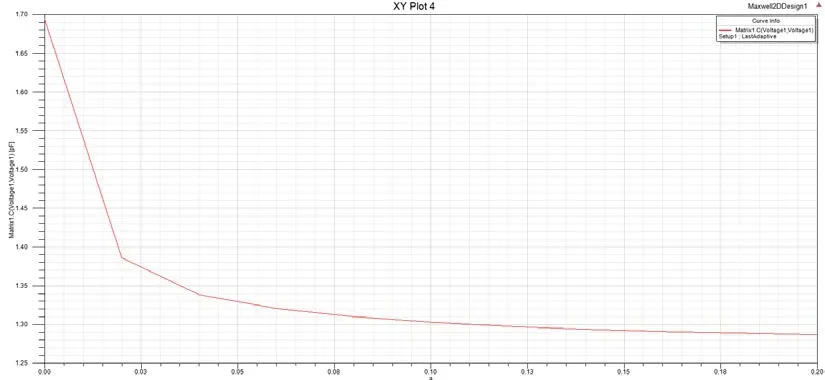
图8 改变板间距仿真电容值

图9 改变板间距仿真电场分布
由图8和图9可以看出,电容随着板间距的变大,电容值逐渐减小,电场强度也逐渐减小。当间距增大范围在0~0.024mm之间时,电容值成线性变化,极板间距离继续扩大,电容变化幅度减小,近似于反比关系,由式(7)可知,电容值C于板间距d成反比关系,计算值是在忽略掉边缘效应、寄生电容和外界干扰的情况下得到的,因此仿真结果会在某种程度上跟计算值存在差异。由仿真可知,当板间距离增大到0.05mm后,呈现出和电容C成反比,也就是当板间距离取值为2.05mm时候,边缘效应、寄生电容和外界干扰对电容的影响小,计算值和仿真值的变化趋势相同。接收板的电场强度趋近于直线,分布均匀。
3.2 不同屏蔽下仿真研究
电容角位移传感器的电容变化较小,灵敏度高,极易受到外界电磁场的干扰,外界环境的变化都会影响电容值的精度和传感器电势的变化[9],因此从屏蔽措施方面来研究电容角位移传感器。
图10(a)为未加屏蔽极的电势图,图10(b)是在极板间屏蔽极的电势图,比较两图,可以明显看出当加入极间屏蔽后,电势明显的集中在极板间和发射极板,有效的避免了板间不必要的电容耦合。图10(c)为加极板间屏蔽、外部防干扰屏蔽时的电势图。由于电容角位移传感器是通过测量敏感区域介质的变化,间接测量电容值的变化,当电场强度集中在两静板间,可增加电容的储能能力,提高传感器灵敏度。由图10(a)看出:电场线不仅通过敏感区域,而且还有一部分通过基板到达检测电极,加入极间屏蔽后将这部分电场线切断,而对敏感区域内的电场不造成影响。加入外围屏蔽后,可使得电场集中于敏感区内,消除外部电场的干扰。由图10可明显看出: 加载屏蔽后可有效消除外部电场干扰,减小极间静态电容,提高了传感器的检测精度。
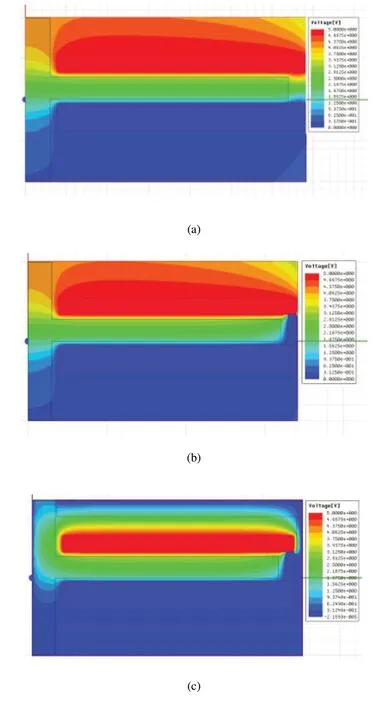
图10 不同屏蔽对电势的影响
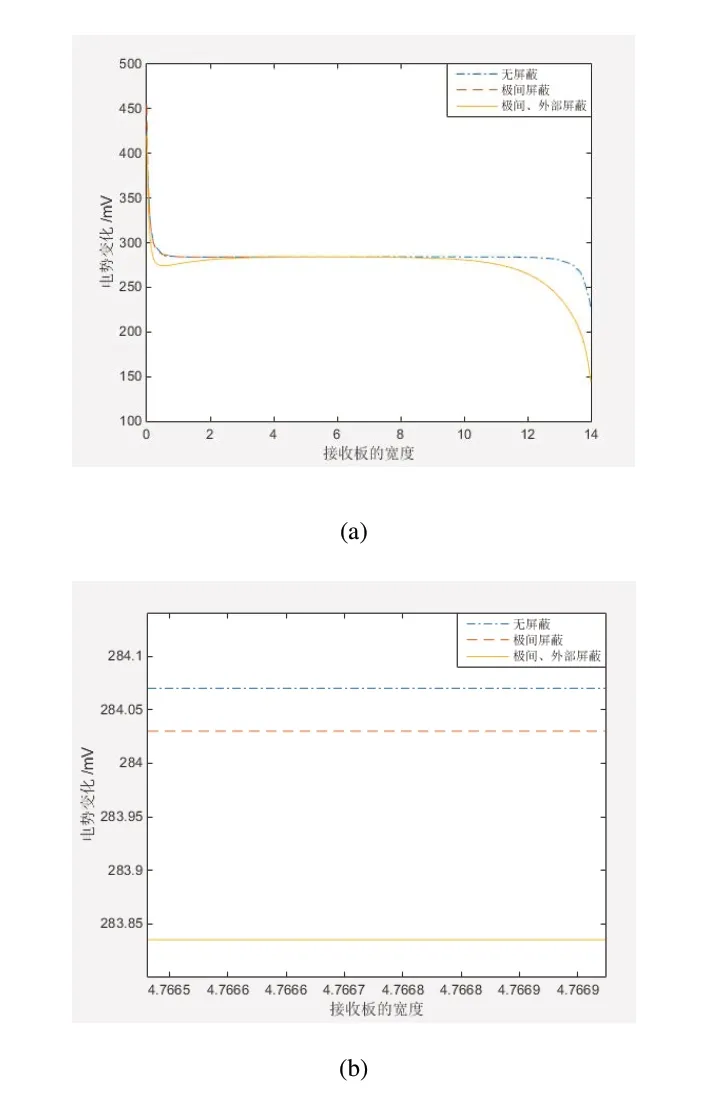
图11 改变介电常数电容变化
图11(a)是在不同屏蔽措施下,接收极板电势分布图曲线图,在接收极两侧存在边缘效应,电势发生突变。图10(b)是图10(a)的局部放大,由图10(b)可以看出,随着屏蔽极的存在,在接收极上的电势发生变化,未加屏蔽时,测出的电势值高于屏蔽后的电势值。图12是电容值的变化曲线分布图,在电容角位移传感器上施加屏蔽措施时,可减少板间敏感区受外界的影响,消除外部电场的干扰,电容的储能能力也随之增强,电容值也逐渐 变大。
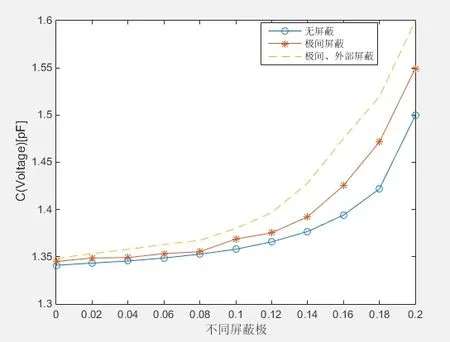
图12 电容变化分布图
4 结论
本文使用ANSYS和MAXWELL电磁场仿真软件,仿真构建了二维、三维电容角位移传感器。根据上述仿真,得出角位移传感器的最佳参数。通过仿真分析传感器在不同状态下电势和电容值的分布情况,可以得出在板间距为0.25mm时,边缘效应的影响对电容角位移传感器的干扰可以忽略。存在极板间屏蔽、传感器外部屏蔽时,可以有效地减少环境对传感器内部的干扰,增大电容的储能能力,增强电容角位移传感器的灵敏度。为高精密传感器的设计提供了依据。
