一种悬吊式恒拉力系统的间接力控制策略设计与仿真验证
2019-08-29孙光耀高海波牛福亮
刘 振,孙光耀,高海波,牛福亮
(哈尔滨工业大学机器人技术与系统国家重点实验室,哈尔滨150001)
1 引言
发射任务之前需要在地面对航天员进行微重力模拟训练[1],悬吊法因为其模拟的失重环境时长不受限制,模拟精度高并且可以实现空间内3自由度的模拟,在目前的微低重力模拟方面应用较多,并取得了诸多成果[2-3]。悬吊式微低重力模拟系统中的恒拉力子系统为航天员提供时时刻刻的恒定补偿力,其恒力精度和抗扰动能力决定了重力补偿的效果[4]。恒拉力子系统的方案目前主要有配重式、弹簧缓冲式、电机+卷筒式和电机+恒拉力机构+卷筒式。配重式的配重物惯量会引起较大的拉力误差,目前应用较少。弹簧式的拉力精度受限于弹簧刚度而无法做到很高。电机+卷筒的主动控制式可以实现较高的拉力精度,但抗冲击效果较差。因此目前应用最为广泛的是电机+恒拉力机构+卷筒式,电机提供主动的拉力控制,恒拉力机构实现对力冲击的缓冲[5]。本文研究的恒拉力系统即为此类恒拉力系统。
目前在恒拉力控制策略研究方面大多采用直接力控制,易于保证较高的拉力精度[6],但力信息可以发生突变,瞬态冲击力需要电机付出瞬间的响应来抑制,对电机提出了很高的要求,增大了系统硬件成本;间接力控制思路为利用位置或速度闭环进行力的控制[7-9],应用最多的为阻抗控制。位置信息无法发生突变,从而保证了控制系统的稳定性,并降低了对电机的要求和控制难度。但对于转角和力的映射比例关系很小的恒拉力机构,因其等效刚度低,故现有的直接用位置或速度对力产生控制的算法无法直接使用。对此,本文提出一种将电机控制恒拉力机构的内部转角对0°的位置跟随来实现对力的恒定控制策略。
2 恒拉力系统方案
用于吸收被控对象的高频扰动的恒拉力机构如图1所示,主要由输入轴、压簧、扭杆和输出卷筒4部分组成。在力矩的传递过程中,如图布置形式的压簧弹性元件表现出负刚度的力矩特性,扭杆元件表现出正刚度的力矩特性,将两种力矩进行叠加,从而在卷筒输出端得到恒定的拉力。
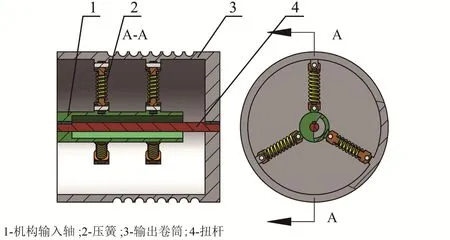
图1 恒拉力机构原理图Fig.1 Schematic diagram of constant-force mechanism
基于恒拉力机构搭建得到图2所示的恒拉力系统,主要由电机传动轴系和电气系统组成。电机传动轴系包含电机、减速器和恒拉力机构。恒拉力机构的输入端和输出端均安装编码器,在输出卷筒上缠绕吊索,并在末端设置拉力传感器。电气系统主要用来完成电机供电和实时控制功能。整个系统可在1.5 m范围内,提供最大1000 N的恒拉力需求。
3 动力学建模
恒拉力系统可简化为图3。电机是整个系统的动力来源,输出力矩为τ;抱闸主要在系统断电后进行制动,并锁住当前位置。恒拉力机构输入端直接和减速器的输出轴相连,等效转动惯量为J1;输出端和卷筒吊索相连,等效转动惯量为J2。吊索拉力大小为F;令恒拉力机构的输入转角为θ1, 输出转角为θ2,θ2同时也是已经承载负载后的角位移。

图2 恒拉力系统主要构成图Fig.2 Main components of constant-force system
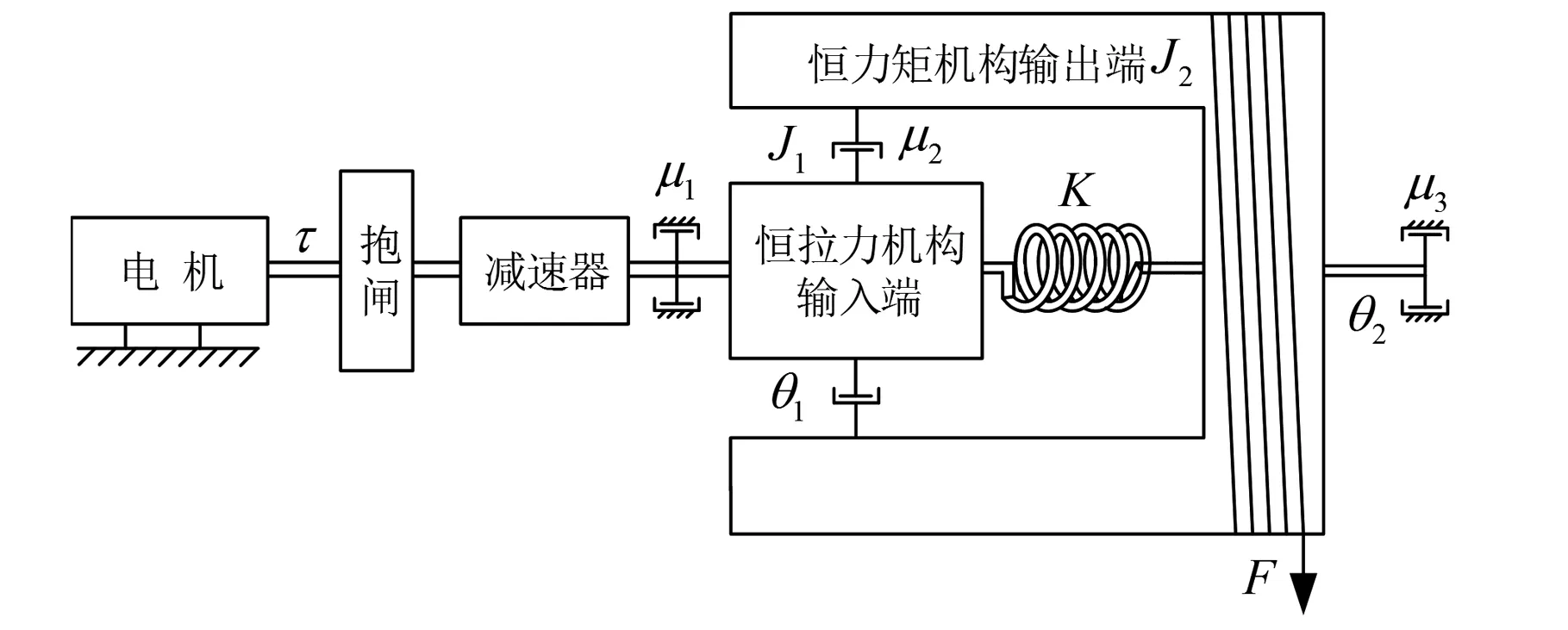
图3 恒拉力系统原理简图及参数标注Fig.3 Schematic diagram and parameter marking of tensioning constant-force system
基于牛顿第二定律,建立恒拉力系统的动力学模型。电机驱动方程如式(1):

式中:μ1、μ2分别为为电机轴和恒力机构输入端、恒力机构输入和输出端的等效粘滞摩擦系数;τtorsion为恒拉力机构等效扭簧提供的扭转力矩。式(1)中的J可以表示为式(2):
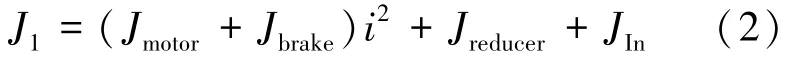
式中:Jmotor、Jbrake、Jreducer和JIn分别为电机、抱闸、减速器和恒拉力机构输入端的转动惯量;i为减速器的减速比。
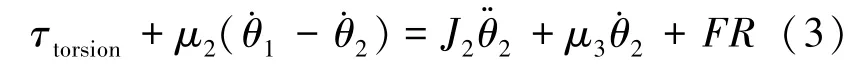
恒拉力机构方程为式(3):式中:μ3为恒拉力机构输出端和基座之间的等效粘滞摩擦系数;R为输出卷筒的半径。
假设理想扭矩为τd,通过实验拟合得到恒拉力机构的等效扭簧提供的扭转力矩τd,通过实验拟合得到恒力机构的等效扭簧提供的扭转力矩τtorsion,忽略高次微小项得到式(4):
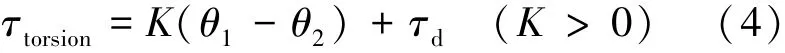
式中:τd为力矩设定值。假设期望绳索拉力为Fd,实际绳索拉力可表示为式(5):
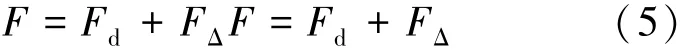
将式(4)代入式(3)可以得到式(6):
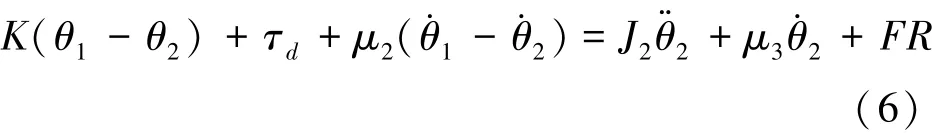
将式(5)代入式(6),化简得到式(7):
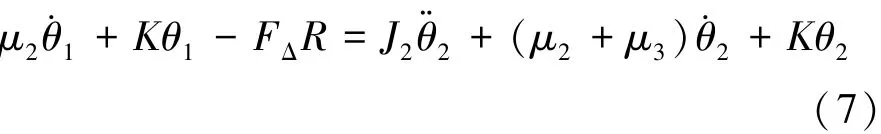
将电机转角θ1和恒拉力机构输出转角θ2作为系统的输入,输出为吊索力误差FΔ,解得系统传递函数如式(8):
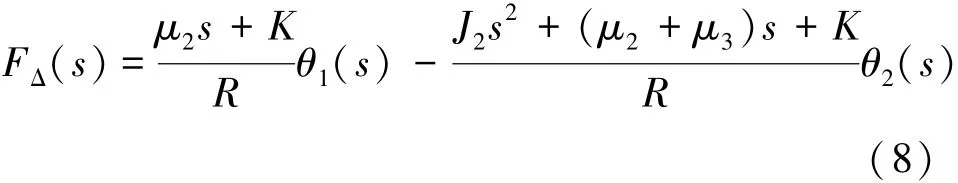
4 间接力控制策略设计
串联张紧式恒拉力系统的控制目标为让末端吊索的拉力稳定在允许误差范围内,吊索力和串联张紧式恒拉力机构输入输出端转角差在静态工作点附近有近似线性的关系,因此理论上通过控制转角差为0°即可实现拉力在设定点附近的恒定控制,即间接力控制方式。
由于串联张紧式恒拉力系统的动力学建模只建立了低频特性传递函数,忽略了高频模型误差、非线性项等的影响,系统辨识也很难准确测量其各项参数,基于模型的控制器设计较为复杂,很难取得较好效果。因此控制器选用不依赖模型的不完全微分PID控制器,配合矫正环节实现对串联张紧式恒拉力系统的控制[10-11]。
电机驱动器有力矩、速度和位置3种控制模式。从力控制角度考虑,直接基于驱动器的力矩环进行上层算法的设计是比较直接的方式,力矩环的闭环速度在3环中最快,速度环次之,位置环最慢。力矩环状态下电机轴的转角和转速都将不受控,力矩环严格按照控制器指令执行,无法保证恒拉力机构输入输出端转角差始终在0°附近,会导致机构受干扰后跳出恒拉力机构的最佳工作区,因此力矩环不宜采用。速度环快于位置环,并且进行电机的调谐后,驱动器的速度环将电机轴到恒拉力机构输入端之间的摩擦等成分全部进行闭环,调谐好的电机在低频区可看做特性很好的速度源,综合考虑后选择驱动器速度环作为控制闭环的内环[12]。
恒拉力机构的输入角和输出角之间的差值在±15°范围之内;为了增大负载的移动行程,利用电机带动整个恒拉力机构旋转。为了使吊索力稳定在设定的拉力上,恒拉力机构应该始终工作在静态工作点附近,即 Δθ=(θ1-θ2)=0。 因此,将吊索的拉力控制转换为电机的转角控制。因为吊索力的反馈信息是容易出现尖峰突变波动的,而机构的转角信息是力信息的二重积分,其不具备尖峰突变的特点,因此更易保证系统的稳定性。
假设电机的跟踪控制效果较好,取极限情况θ1=θ2, 将式(8)化简得到式(9):
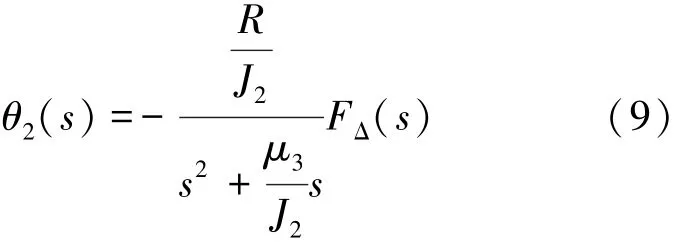
从式(9)可知,在该控制策略下,恒拉力系统的拉力误差值为恒拉力机构输出端的惯性力和动摩擦力,其量值相对于负载载荷很小,因此可以接受。
当θ1=θ2时,,从式(4)得出式(10):

即串联张紧式恒拉力机构内部的力矩是恒定的,从式(3)得出式(11):
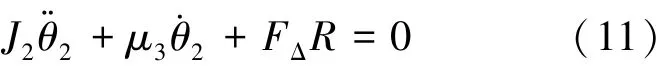
如果扰动FΔ一直存在,类似于用恒定力推动摩擦面上的一个物体。对于系统如果给定一个恒定扰动FΔ(s),系统会一直加速最后匀速,最终匀速速度为式(12):

如果摩擦足够小,输出端将一直加速下去,加速度(角加速度)为式(13):

由式(13)可知,串联张紧式恒拉力系统是一个对吊索悬吊的负载来说完全失重的系统。吊索力仍然满足F=Fd+FΔ,如果FΔ属于一个作用了一段时间就消失的量,则其消失后F=Fd,吊索力依旧等于设定值,这也符合失重下负载有扰动后上下运动,扰动消失后匀速运动的现象。
基于驱动器速度环的位置闭环控制框图如图4所示。控制器输入信号为位置误差信号,输出为电机转速指令,机构输出端的位移θ2(s)到吊索力误差FΔ的传递函数G(s)由式(9)得出。
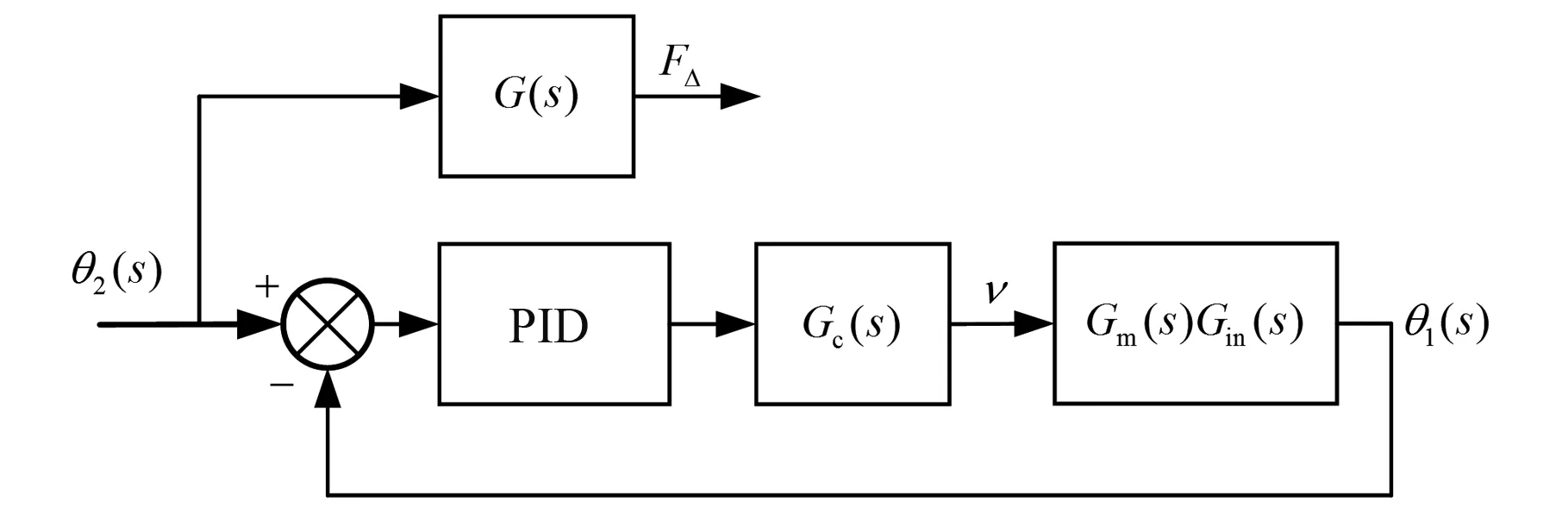
图4 基于电机速度环的位置闭环控制框图Fig.4 Position closed-loop control block diagram based on motor speed loop
5 联合仿真验证
通过MATLAB和ADAMS的进行间接力控制的联合仿真验证。将恒拉力机构三维模型导入ADAMS,添加弹簧、扭杆等弹性环节和摩擦阻尼环节,用一个大的质量球(100 kg)表示运动负载,上面的一个轻质小球(0.01 kg)表示吊索的上端,大球和小球之间添加与位移相关的相互作用力。刚度设置到足够大,代表刚度很大的钢丝绳吊索。ADAMS仿真模型如图5所示。

图5 ADAMS仿真模型Fig.5 ADAMS simulation model
使用MATLAB建立控制系统如图6。向ADAMS模型输入有负载大球的竖直方向运动速度信号,将恒拉力机构的输入输出端的转动角度进行做差后作为PID的输入偏差信号。该闭环中设置了前馈环节,将负载的运动输入信号进行前馈,同时给负载增加白噪声的扰动,扰动的信息当做纯干扰,因此不做前馈。最后的输出量为吊索的力。
输入信号为2000sin(2π10t)mm的正弦激励信号,最大速度为2 m/s,频率为10 Hz,并且加入能量较大的白噪声作为干扰,这是一个对于恒拉力系统来说较为恶劣的工况。经过10 s的联合仿真后得到的力曲线如图7所示。从图中可以看出,最大的吊索拉力误差为5 N,相对于1000 N的负载拉力来说,该误差较小,可以满足要求。
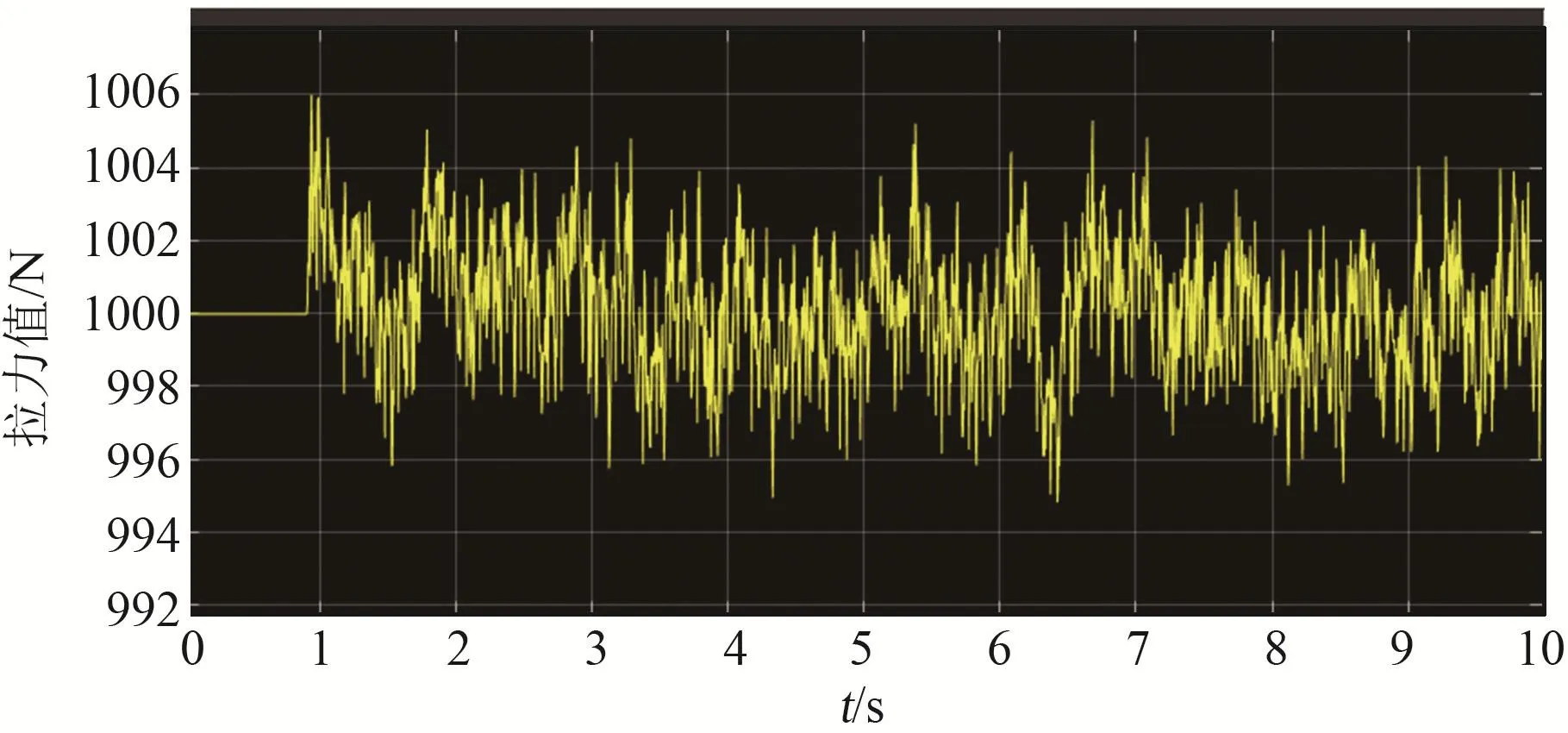
图7 正弦激励仿真力曲线Fig.7 Simulated force curve under sinusoidal velocity
对负载输入2 m/s的匀速运动信号,得到的力曲线如图8所示。从图中可以看出,最大的力误差为70 N3σ,大于正弦运动的误差值,造成此结果的原因是速度较大,前面的正弦信号只有峰值能达到2 m/s,而这个实验是一直2 m/s,同样也存在白噪声的激励,在本来就高速的基础上加噪声,就造成了较大的拉力误差。该误差值虽然较大,但是考虑到2 m/s的速度已经是很恶劣的工况,并且存在较大的扰动,因此该拉力精度可以满足要求。

图8 匀速激励仿真力曲线Fig.8 Simulated force curve under uniform velocity
6 结论
1)所设计的间接拉力闭环控制策略,可实现系统的稳定和拉力的抖动抑制;
2)通过联合仿真验证了控制策略的抗干扰性,幅值2 m/s,频率10 Hz的正弦激励下,拉力误差为0.5%;恒速2 m/s的激励下,拉力误差为7%。可以满足微低重力模拟的要求。
