复合材料编织带平面承力层结构有限元模型

刘 敏,袭建人,房光强,刘 钰

(1.山东大学土建与水利学院,济南250061；2.山东大学材料科学与工程学院,济南250061；3.上海宇航系统工程研究所,上海201108)

1 引言

2016年4月美国太空探索技术公司将Bigelow公司的BEAM充气太空舱成功与国际空间站完成对接,并顺利完成太空舱充气膨胀,这种可充气膨胀展开太空舱重量轻、发射成本低,并可提供较大的居住空间和更好的空间防护[1]。可充气太空舱通常采用多层复合材料制造,满足不同的功能性和结构性要求,如图1所示[1]。

可充气太空舱结构的核心部分是其承力层,要满足整个太空舱的结构性能要求,同时要求具有折叠和膨胀展开功能。为达到这一目的,承力层通常设计为由高强度纤维带交叉编织在一起,如图2所示[2]。

图1 BEAM太空舱结构示意图[1]Fig.1 Schematic diagram of BEAM space cabin structure[1]

图2 承力层结构示意图[2]Fig.2 Schematic diagram of load bearing layer[2]

纤维织物本身由纤维束按照编织模式由经纱和纬纱编织而成,在承受力的作用时,由于经纱和纬纱相互作用,而使其力学性能具有复杂的几何非线性和接触非线性特征,导致承力层的结构计算难度大大增加。将平面编织纤维织物等效为单层均质膜可以实现圆柱面的折叠和展开的模拟[3],而将平面编织纤维织物简化为薄板或壳,按照正交各向异性的均质连续体进行计算是前期该领域研究的普遍做法[4-6],基于编织物的细观结构特点建立的织物膜理论则进一步体现了纤维织物的力学特性[7]。从纤维束的细观结构入手,Parsons等[8]通过将每束纤维视为连续体,考虑各纤维束间的接触,并允许纤维束之间具有滑动特性,更真实地反映了平面编织纤维织物特性,更好地实现了力学性能的模拟[8]。然而将文献[8]中的方法应用于实际的工程结构,将会由于计算规模太大而难于实际应用。

鉴于现有的计算能力,本文尝试将平面的编织纤维带视作连续的壳体,考虑各纤维带之间的相互接触作用和承受载荷作用下的相互之间的滑动,并根据编织纤维带的力学特性,探讨更适于解决编织纤维带构成的承力层结构力学计算模拟方法。

2 理论与建模

2.1 平面壳单元的有限元理论

根据平面壳单元理论[9],空间壳单元在其局部坐标系中,每个节点有5个自由度,单元任一点的位移向量f写为式(1)。

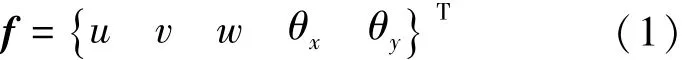
式中,u,v,w分别为x、y和z坐标轴方向的平动位移分量,θx和θy分别为绕x、y坐标轴的转动位移分量。若采用4节点矩形的壳单元,则节点i的位移向量fi及其对应的位移分量为式(2)。

壳单元中位移分量ui和vi对应的薄膜效应的单元刚度矩阵为式(3)。

壳单元中位移分量wi、θi和θi对应板单元的用于表示弯曲效应的单元刚度矩阵为式(4)。

式(3)和(4)中上标m、b分别表示对应薄膜效应和弯曲效应的单元刚度矩阵。将式(3)和(4)分别扩充为20×20的矩阵,式(3)和(4)中的分块矩阵和按照式(1)右端项的位移分量顺序对应放置扩充矩阵中,在没有对应分块矩阵的位置填充O并将两式相加得到式(5)。

按照式(5)的单元刚度矩阵得到的有限元方程,可以求解包含薄膜效应和弯曲效应的力学问题,而在式(5)中去掉弯曲效应对应的刚度矩阵,即将带有字母b的分块矩阵置为O,则可用于求解只考虑薄膜效应的力学问题。但在进行如图2所示编织带结构的力学分析中,因可充气式太空舱的承力层,需要折叠和充气膨胀展开,其弯曲刚度一定很小。对这样的编织带构造的结构进行力学模拟,传统做法常只考虑膜应力的壳单元,从而低估了编织带的抗弯曲性能。而采用式(5)的壳单元进行力学模拟,由于将编织带的厚度完全计入其弯曲刚度,则明显过高地计入了编织带的弯曲刚度,与实际情况相差较大。因此本文提出基于薄膜效应壳单元附加一定弯曲刚度的混合单元来解决可充气膨胀展开式太空舱的承力层结构的力学计算。

2.2 平面编织织物壳单元的有限元理论

为求解编织带结构的力学问题,在节点自由度和单元刚度矩阵元素维数不变的条件下,将式(5)修正为式(6)。

上式中右边的第1项为按照编织带几何尺寸和材料参数建立的只考虑薄膜效应的单元刚度矩阵,第2项则为修正项,使原有单元增加一定的弯曲刚度。根据壳单元理论,增加弯曲刚度的同时,也带来一定的薄膜效应。因此为便于对比分析弯曲刚度的影响规律,弯曲刚度的修正是基于编织带的厚度,再缩减一定百分比来实现,在此基础上探讨弯曲刚度的修正量对编织带结构力学性能的影响。对于像编织带这样的结构,由于弯曲刚度很小,其给出厚度的缩减百分比较大。

为了减少计算量,原本由经纱和纬纱交织而成的具有离散结构特点的编织带,将其宏观性能简化为用表观宽度和厚度表示的平板。编织带实际上具有一定的各向异性的宏观特性,但其各向异性参数的测试十分困难,考虑到编织带在实际承载中以承受单向拉伸为主,因此将编织带简化为各向同性材料,其弹性模量按照实际的测试数据选取。

2.3 平面编织承力层结构有限元模型

图3为平面平纹编织带结构,依此方式建立有限元模型,模型中横竖方向各采用7条编织带,编织带的横截面尺寸为25 mm宽,1 mm厚,长度为265 mm,材料的弹性模量为30 GPa。编织带的4个外边缘,全部平动位移约束,转动自由度自由。编织带的相互接触面不考虑摩擦效应。承力层结构主要承受内部压力,因此只在中心的3×3共9个上表面施加0.1 MPa的均布压力。由于只考虑薄膜效应的有限元计算涉及到几何非线性,因此按照软件的要求,将单元网格划分为三角形单元,即将单元中的4节点中的2个节点合并(图3(b))。计算采用ANSYS软件进行,弯曲刚度的调整取不同编织带厚度的百分比进行,混合单元的形成是用同一位置的一组节点同时生成只考虑薄膜效应的单元和具有较小弯曲刚度的壳单元。有限元模型单元参数的计算分组见表1。

3 结果与讨论

3.1 计算结果

3.1.1 薄膜单元计算结果

图4为只采用薄膜单元的垂直位移和应力分布图。图5为中心编织带的x方向和z方向的应力分布图。

从图4(a)中可以看出,尽管编织带结构是交叉编织而成,但垂直方向的变形就像是一张带有孔的平板变形一样,具有很好的整体性。最大的垂直位移为-5.999 mm,位于编织带的中心。从图4(b)编织带中x方向的应力分布可以看出薄膜应力呈现出较为均匀的分布,最大数值为36.31 MPa,从中心向边缘方向,应力数值逐渐减小。图5结果进一步显示,x方向的应力沿x方向和z方向,应力数值均呈现小幅的变化,最小33.73 MPa,最大36.31 MPa。编织带中z方向的应力数值均很低,在±0.5 MPa之内,这说明编织带相互之间的接触作用并没有改变其单向应力状态的性质,这样的结果与传统编织带单向承载能力的设计一致。

图3 平面平纹编织带结构及其有限元网格图Fig.3 The geometry and FEM meshing diagram ofwoven fabrics structure

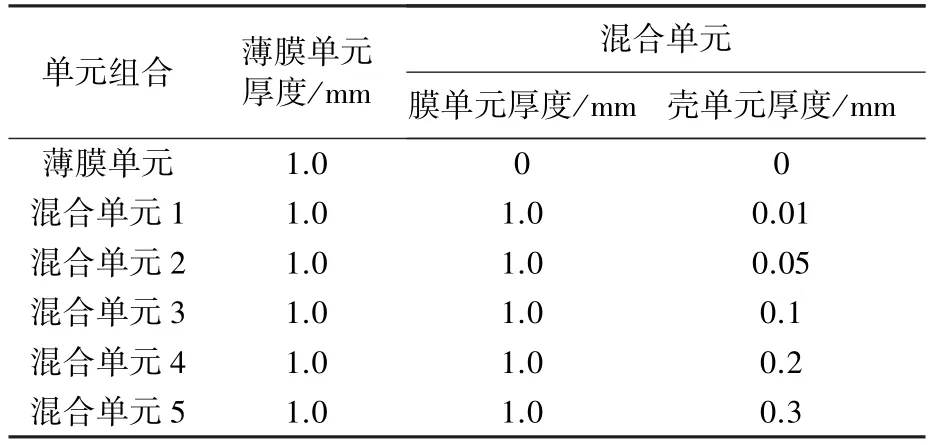
表1 单元厚度情况分组Table 1 Thickness of the membrane and hybrid elements

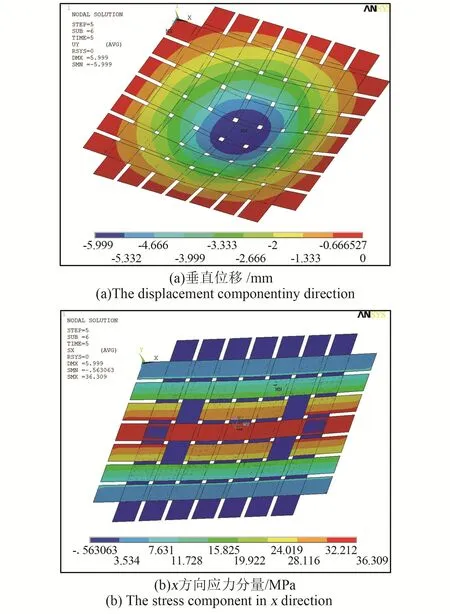
图4 平面编织结构在0.1 MPa压力作用下的位移和应力分布图(薄膜单元)Fig.4 Distribution contour of displacement and stress in the plain woven fabrics structure at 0.1 MPa(only membrane element)

3.1.2 混合单元计算结果

图6为采用薄膜单元加0.1 mm厚度的壳单元,即采用混合单元模型得到的x方向应力分布图,图中看出编织带的正面和背面的应力数值不同,最大应力值在背面,数值为50.23 MPa,而同一点的正面,数值为45.63 MPa。图7(a)为中心编织带的x方向应力分布,最大应力值是位于中心部位的临近区,而图5(a)应力最大值则在中心部位。

图7(b)为中心编织带z方向应力分布,其应力数值相对于只采用薄膜效应单元的计算值要大得多,中心部位的 2个边缘数值最高,达到20.63 MPa。

不同弯曲刚度的混合单元的应力分布与图6所示的规律相似,只是在数值有一定的差异(表2)。由于对称关系,另一个方向的编织带,亦即沿z方向布置的编织带的z方向的应力分布与图6和图7中的x方向应力分布相同。

图5 中心部位编织带在0.1 MPa压力作用下应力分布图(薄膜单元)Fig.5 Distribution contour of stress in the center of plain woven fabrics at 0.1 MPa(only membrane element)

图6 平面编织结构在0.1 MPa压力作用下的应力分布图(混合单元)Fig.6 Distribution contour of stress in the plain woven fabrics structure at 0.1 MPa(hybrid element)

为分析壳单元的弯曲刚度对混合单元计算结果的影响,选取壳单元的厚度值从0.01～0.3 mm之间变化,即壳单元厚度的变化是编织带厚度的1%～30%。从表2可以看出,壳单元的弯曲刚度越大,其垂直位移越小,从薄膜效应单元的-5.999 mm,减少到混合单元的-5.209 mm,垂直位移数值的绝对值减少了13.2%。相对于垂直位移影响来说,混合单元的采用对x方向和z方向应力的影响较大。混合单元中,当弯曲刚度较小时,同等条件下产生数值为52.62 MPa的x方向应力增加幅度高达45%。同样z方向应力尽管数值在20 MPa左右,但增加幅度较大。因此只采用薄膜效应单元会高估结构的静态承载能力。

表2中的数据也表明,壳单元的厚度值从0.01～0.3 mm变化,以0.01 mm的计算结果作为参考,则垂直位移的变化幅度的绝对值为8.412%,x方向应力变化幅度的绝对值为11.78%,z方向应力变化幅度的绝对值为15.92%。

3.2 讨论分析

1)对于像编织带这样的平面织物来讲,传统上为计算简化常忽略其弯曲刚度,利用只考虑薄膜效应的薄膜单元进行结构的计算分析,这样做是可表征其主要承载特性。从计算结果中可以发现(图5(a)),平面织物结构承受局部压力载荷会造成编织带的局部薄膜应力增加,这一点与将编织结构进行均匀简化的计算结果不同。同时可以注意到,局部的承压会导致织物在受压处产生较大的局部下凹,且这种局部下凹不仅沿编织带长度方向存在,同时沿编织带平面内的横向也有一定程度的存在,从而造成其薄膜应力不均匀分布,但应力状态基本处于单向应力状态。

2)编织带由于采用经纱和纬纱交叉编织在一起,具有较高的单向承载拉伸的能力,同时也具有较小的弯曲刚度,以便折叠弯曲之用。这个较小的弯曲刚度尽管对编织带结构的刚度影响较小(13.2%以内),但对工作应力会带来较大的影响。如果壳单元的厚度只取原薄膜单元厚度的10%,即壳单元的弯曲刚度只取原厚度刚度的千分之一,则沿编织带纵向的最大应力计算值会增加45%,而编织带横向的最大应力计算值会从很小数值增加为20 MPa左右(表2)。同时应力分布规律也与只采用薄膜效应单元的完全不同,纵向应力数值较高的区域并不位于中心编织带的中心区域,而是在相互垂直编织带交叉重叠区域,且最大纵向应力位于长方形的交叉重叠区的4个角点处,而中心区域的应力值低于4个角点处的应力值(图7(a))。横向应力较大的区域仍位于中心编织带的中心区域,但最大的横向应力出现在相互垂直编织带交叉重叠区域的2个边缘上(图7(b))。

图7 中心部位编织带在0.1 MPa压力作用下应力分布图(混合单元)Fig.7 Distribution contour of stress in the center of plain woven fabrics structure at 0.1 MPa(hybrid element)

表2 不同单元计算结果比较Table 2 Comparison of calculation results of different elements

3)对比图5和图7,可以看出编织带的整体变形规律基本相同,即压力作用区出现明显的下凹,中心区域较为平坦,垂直位移数值较大,但其局部曲率较小；压力作用区的边缘垂直位移数值较小,但其局部曲率较大,这也是具有弯曲刚度的编织带其应力的高水平点位于中心编织带重叠区的边缘的原因,而只采用薄膜效应单元则无法模拟这种力学特性。

以上分析表明,对于编织带构成的平面织物结构,采用不同的单元类型对结构静态应力变形模拟计算有较大的影响,采用混合单元更能反映编织带的受力特点。从混合单元的计算结果可以看出(表2),垂直位移和应力计算值对壳单元厚度值的敏感性较低,其变化幅度在16%以内。在编织带的弯曲刚度无法准确获知的条件下,利用基于混合单元的有限元模型进行编织带结构的静态力学分析可更准确地反映出编织带固有的力学特性。由于壳单元厚度值不仅增加弯曲刚度,同时增加薄膜刚度,会对编织带中的薄膜应力计算带来较大的影响,所以取相对较小的壳单元的厚度值更接近编织带的实际承载状态。

因此对于像编织带这样的结构件而言,目前用于结构分析的弯曲刚度的实验方法测定仍属空白,在此条件下,选取具有较小弯曲刚度的混合单元有限元模型进行其结构力学计算分析是值得推荐的可行方法,可以更准确地模拟编织带结构的力学响应。

4 结论

1)采用薄膜效应单元并考虑编织带之间相互接触的有限元模型,在非均匀承载条件下,每根编织带内会呈现不均匀的纵向应力分布,更准确体现膜的受力特征。但由于薄膜效应单元不能精确地反映编织带的弯曲刚度,导致编织带基本呈现单向应力状态,无法真实地反映局部接触区域的应力状态,从而高估编织带的静态承载能力。

2)采用以薄膜效应单元为基础,叠加具有较小弯曲刚度的壳单元形成混合单元来建立有限元模型,更能准确地反映编织带的实际承载效应,更真实地评定其静态受力状况,在目前缺少编织带弯曲刚度实验方法的条件下,是一种更好的评估编织带织物结构的静态力学性能的有限元模型。

3)基于混合单元的有限元模型,对壳单元弯曲刚度取值的敏感性较低,可采用较小数值弯曲刚度的混合单元有限元模型进行编织带结构力学分析,以更准确地模拟编织带结构的静态力学响应。