复杂富水地层下盾构机掘进速度模型建立与参数优化
2019-08-28王强
王 强
(山西小浪底引黄工程有限公司,山西 太原 030002)
近年来,国家对基础建设越来越重视,盾构施工法因其针对性强、机械化程度高、劳动强度低、施工进度快、对周围环境影响小等诸多优点,被广泛应用于各大城市地铁隧道建设中[1- 2],盾构机作为隧道建设的主要施工设备,其综合掘进性能直接影响隧道施工的质量与工期,主要掘进参数的合理设置能够提高掘进效率,降低施工成本,对改善施工状态起到良好的作用。
国内外学者对掘进参数进行了大量研究,Krause和Maidl等[3- 4]建立了盾构机刀盘总推力及刀盘扭矩的经验计算公式;Rehm[5]推导出组成刀盘扭矩的四部分;朱现磊等[6]研究了煤巷掘进速度的影响因素,并提出解决方案;路平等[7]结确定了盾构机掘进参数的最优取值范围并制定控制地表沉降的措施;张厚美[8]建立了软土地层下刀盘扭矩及掘进速度的数学模型;王洪新[9]等推导出刀盘总推力、土仓压力、掘进速度的数学表达式;管会生[10]分析了盾构机刀盘总推力、刀盘扭矩的各个组成部分,给出理论分析公式,并利用盾构机施工实测数据进行验证;李潮[11]分析了刀盘总推力及刀盘扭矩各部分组成及各参数对计算结果的影响度,并建立力学模型;陈仁鹏[12]等对复杂地层下盾构机的刀盘总推力与刀盘扭矩的影响因素,提出二者的计算修正公式,并通过试验验证计算公式的正确性;杨全亮等[13]对复杂地层中盾构机掘进参数间的规律进行深入研究,对部分掘进参数进行定量预测;李金锁[14]通过控制复杂线路下盾构机参数,进而控制建筑物的沉降;杨旸[15]基于南宁地铁2号线,确定了圆砾地层土仓压力取值范围的计算方法。
可以看出,对于盾构机掘进参数的确定和优化一般根据具体项目的工程地质和设备参数来确定,而对于复杂富水地层掘进参数的研究目前较少。本文以山西小浪底工程为背景,研究盾构机掘进参数间的关系,在复杂富水地层掘进中调整合理的盾构机参数,以获得较高的工作效率。采用多元非线性分析方法,分别以掘进速度和刀盘扭矩为因变量,建立掘进速度和刀盘扭矩与其他主要掘进参数之间的数学模型,并对掘进速度的数学模型进行参数优化,得到复杂富水地层下盾构机掘进的最优速度,对提高盾构机掘进效率及降低施工综合成本具有重要意义。
1 工程概况
山西省小浪底引黄工程引水干线盾构隧道施工工程采用盾构施工法,本标段隧洞起始于小浪底水库库区,终止于闻喜县内的吕庄水库,线路全长5516.9m,隧洞外径为5.22m,内径为4.52m,管片环宽1.5m,设计纵坡1/3000。盾构施工段地形总体向隧洞出口方向逐渐降低。主要掘进工作区域包括:盾构机正常掘进段、盾构机始发竖井、发射区、盾构机后配套段及盾构机拆卸段。
工程区位于黄河一级支流涑水河的左岸,区内地下水类型可分为变质岩类裂隙水和松散岩类孔隙水,本段洞线多位于地下水位以下,由大桩号向小桩号方向水位逐渐降低,地下水位高出洞底最大约105m。场区大部分地段为富水地段,包括断层破碎带、砂土层,特别是粉土、中细沙、圆砾土等主要含水层,富水性较好,具有中等-强透水性,局部地段地下水与地表水具有一定的水力联系,基岩裂隙水在构造碎裂带中非常发育,水量丰富,连通性好。水头压力大,属高承压水。沿线范围内上覆第四系全新统冲洪积层、晚更新世冲洪积层,下伏基岩为震旦系混合花岗岩。隧道围岩为山前冲洪积物,地层结构复杂,地层分布韵律差,沉积杂乱。
依据盾构机本身性能和隧道工程地质情况,经过各种类型盾构机进行比较,该项目将使用德国Φ5530mm泥水平衡盾构机,刀盘采用中间支撑方式,主轴承外径Φ2600mm,刀盘开口率为28%,刀盘后壁设置搅拌棒,如图1所示。
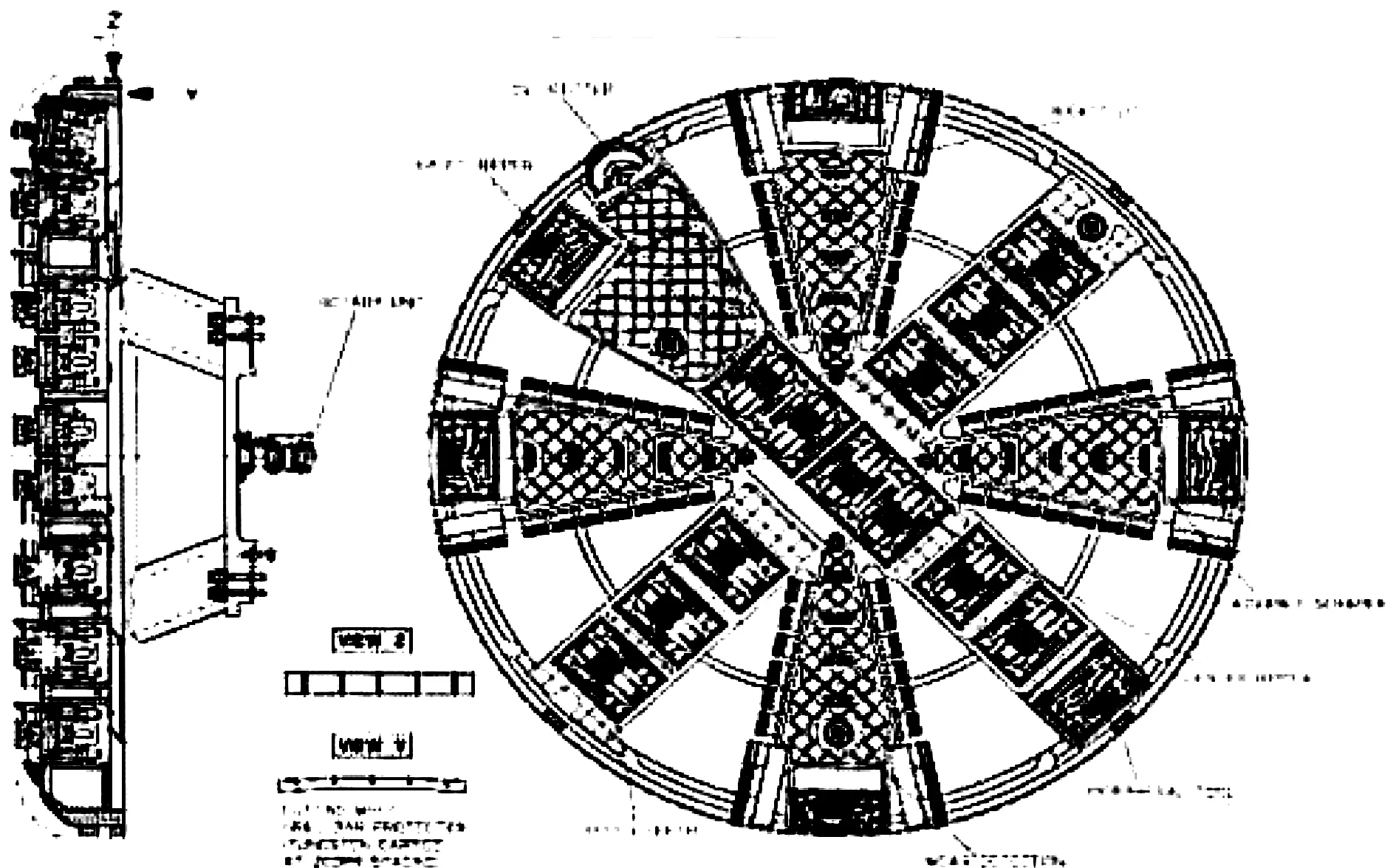
图1 刀盘结构示意图
2 数学模型建立与分析
盾构机掘进系统通过有线和无线网络对盾构机数据进行实时采集并传输,掘进数据包括:刀盘转速、刀盘扭矩、土仓压力、刀盘总推力、掘进速度、盾体铰接总力度。
掘进过程将产生海量数据,为减少人力、物力和财力的浪费,选取每推进一环的数据均值作为采集点数据,本文使用采集的1549—1869环的推进数据进行处理分析。
2.1 掘进速度数学模型建立与分析
掘进速度表示盾构机在单位时间向前开挖的距离,单位mm/min,将直接反映出盾构机掘进地层的难易程度。由于掘进速度影响因素的复杂性,本文以掘进速度为因变量,刀盘扭矩、刀盘转速、刀盘总推力和盾体铰接总力度为自变量建立掘进速度的多元非线性回归模型。
多元非线性回归方程的一般表达式为:
(1)
式中,y—掘进速度,mm/min;x1—刀盘转速,r/min;x2—刀盘总推力,kN;x3—刀盘扭矩,kN;x4—盾体铰接总力度,kN;βi—回归系数;ε-N(0,σ2)。
2.1.1掘进速度与刀盘转速之间曲线拟合模型
利用统计学软件SPSS做曲线拟合,根据非线性函数模型[16],将掘进速度与刀盘转速进行拟合处理,选择拟合度最高的回归模型及对应参数,见表1和图2。
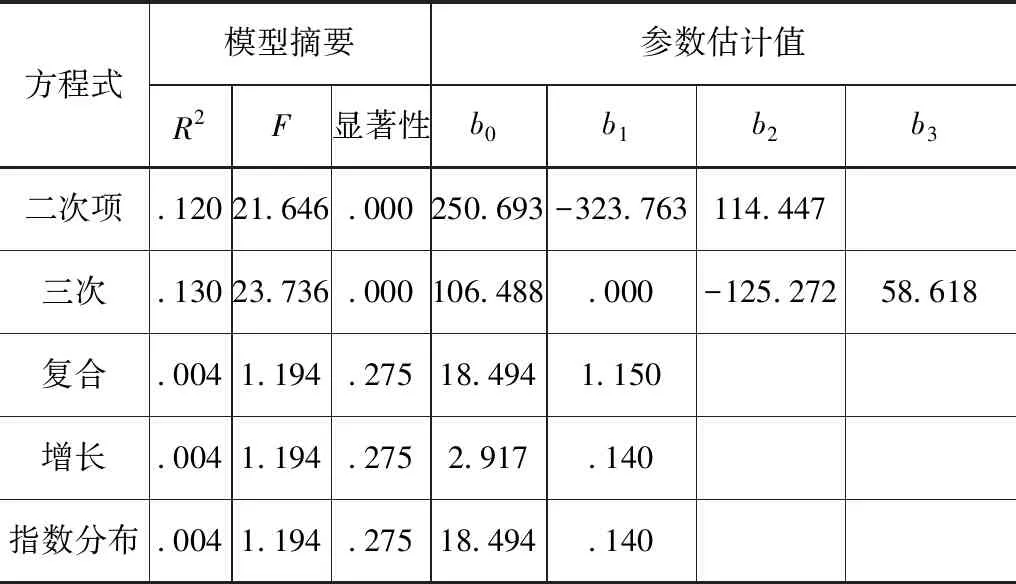
表1 掘进速度-刀盘转速模型摘要和参数估算
注:R2—拟合程度;F—检验值;b0—常数;b1,b2,b3—回归系数。
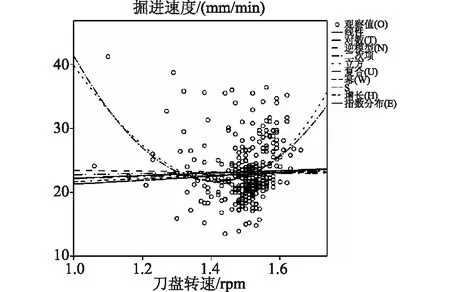
图2 掘进速度-刀盘转速曲线估计拟合图
由表1得,R2的最大值为0.130,对应的检验值F为23.736,检验概率为0.000。
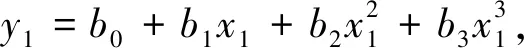
(2)
式中,y1—刀盘转速影响下的掘进速度。
2.1.2掘进速度与刀盘总推力之间曲线拟合模型
将掘进速度与刀盘总推力进行拟合处理,选择拟合度最高的回归模型及对应参数,见表2和图3。
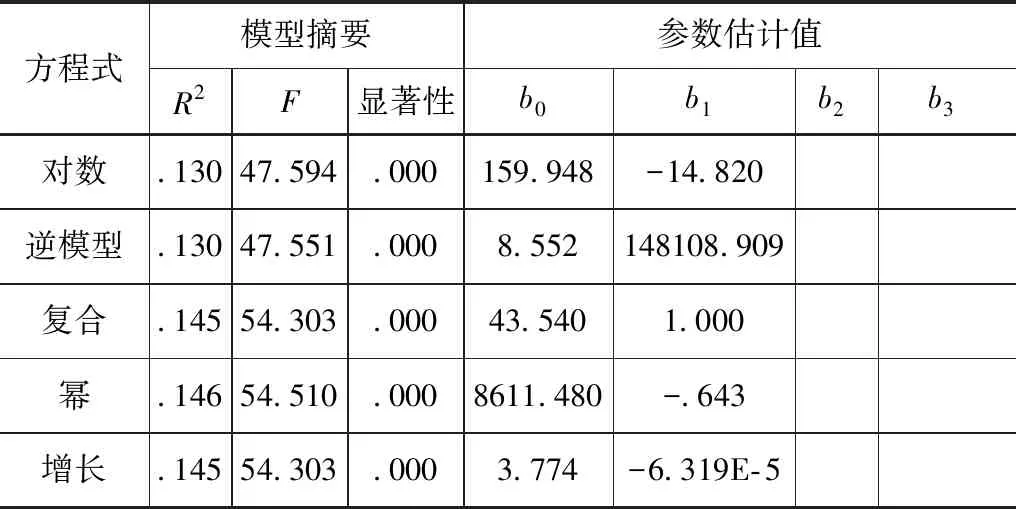
表2 掘进速度-刀盘总推力模型摘要和参数估算
由表2得,R2的最大值为0.146,对应的检验值F为54.510,检验概率为0.000。
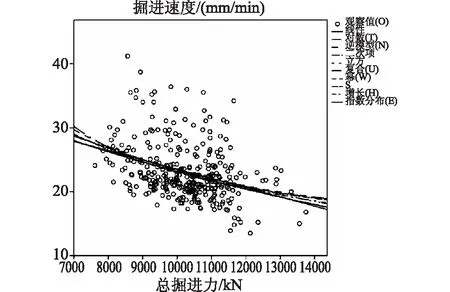
图3 掘进速度-刀盘总推力曲线估计拟合图
由图3得,以刀盘总推力为自变量,掘进速度为因变量进行回归分析,拟合度最高的曲线模型为幂函数y2=b0x2b1,即
(3)
式中,y2—刀盘总推力影响下的掘进速度。
2.1.3掘进速度与刀盘扭矩之间曲线拟合模型
将掘进速度与刀盘扭矩进行拟合处理,选择拟合度最高的回归模型及对应参数,见表3和图4。
由表3得,R2的最大值为0.036,对应的检验值F为11.839,检验概率为0.001。
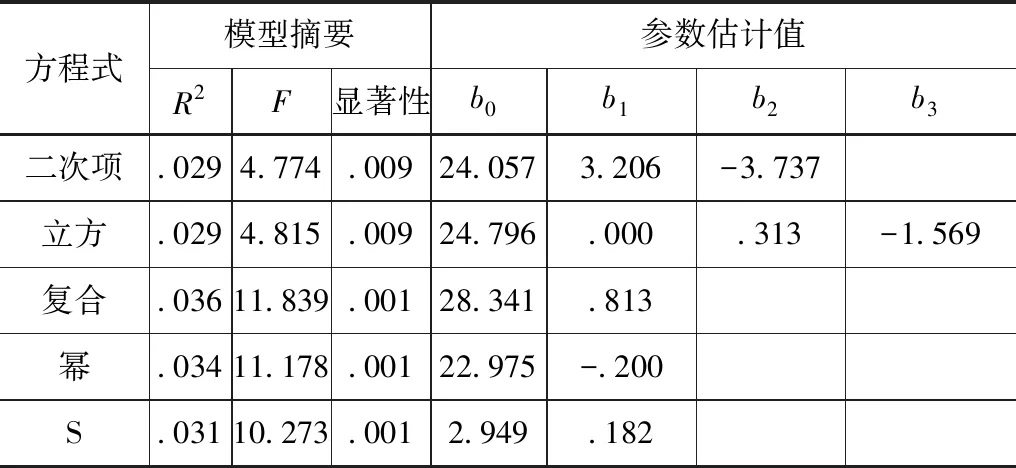
表3 掘进速度-刀盘扭矩模型摘要和参数估算
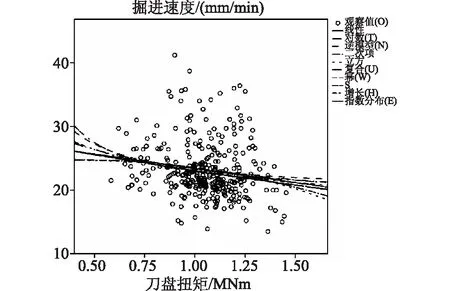
图4 掘进速度-刀盘扭矩曲线估计拟合图
由图4得,以刀盘扭矩为自变量,掘进速度为因变量进行回归分析,拟合度最高的曲线模型为复合函数y3=b0b1x3,即
y3=28.341×0.813x3
(4)
式中,y3—刀盘扭矩影响下的掘进速度。
2.1.4掘进速度与盾体铰接总力度之间曲线拟合模型
将掘进速度与盾体铰接总力度进行拟合处理,选择拟合度最高的回归模型及对应参数,见表4和图5。
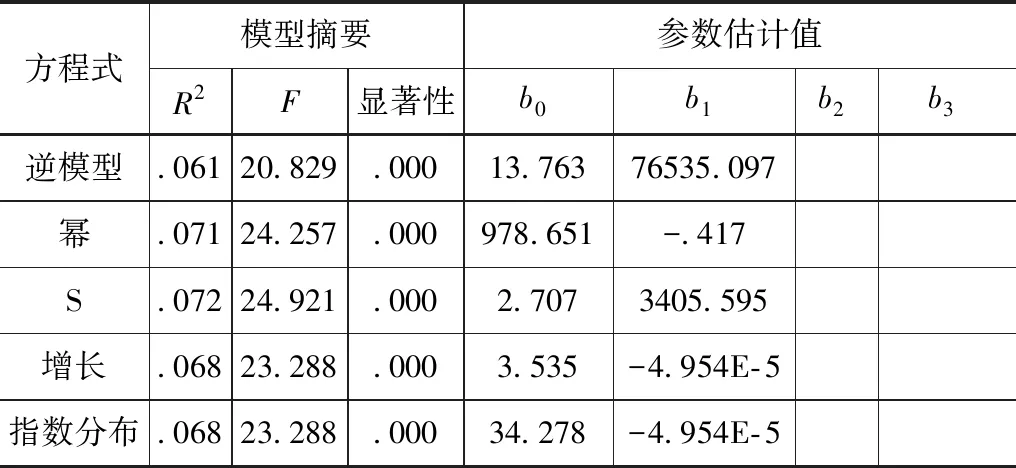
表4 掘进速度-盾体铰接总力度模型摘要和参数估算
由表4得,在所有曲线模型中R2的最大值为0.072,对应的检验值F为24.921,检验概率为0.000。
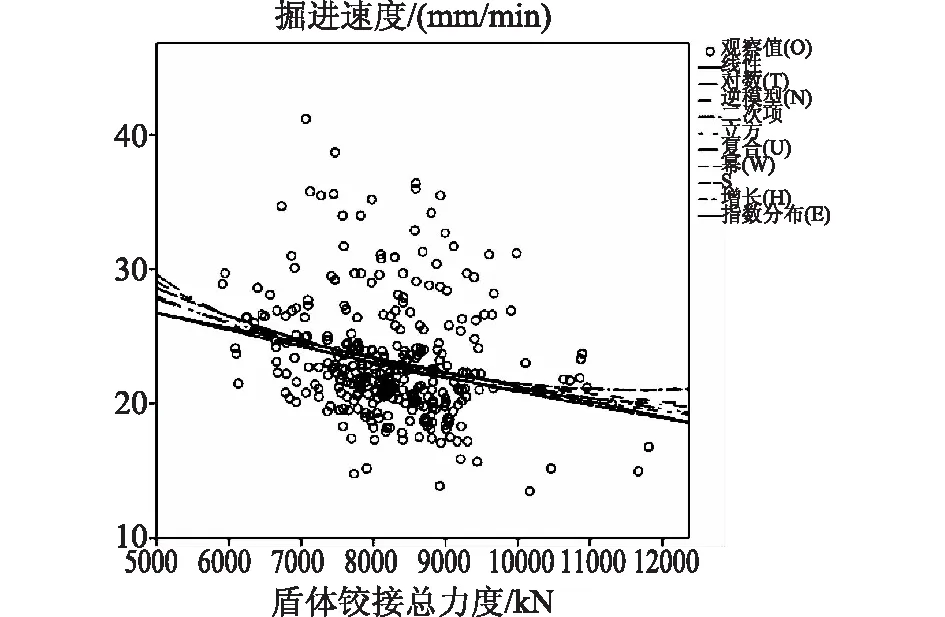
图5 掘进速度-盾体铰接总力度曲线估计拟合图
由图5得,以盾体铰接总力度为自变量,掘进速度为因变量进行回归分析,拟合度最高的曲线模型为S曲线y4=eb0+b1/x4,即
y4=e1.196-9402.123/x4
(5)
式中,y4—盾体铰接总力度影响下的掘进速度。
式(5)中,r0跟踪微分器的快速因子;h0为跟踪微分器的滤波因子;为 v0期望摆角信号;fhan(v1-v0,v2,r0,h0)为最速跟踪控制综合函数[14].
依托y1、y2、y3、y4,采用“逐步”法拟合分析,得到3种模型摘要,见表5。
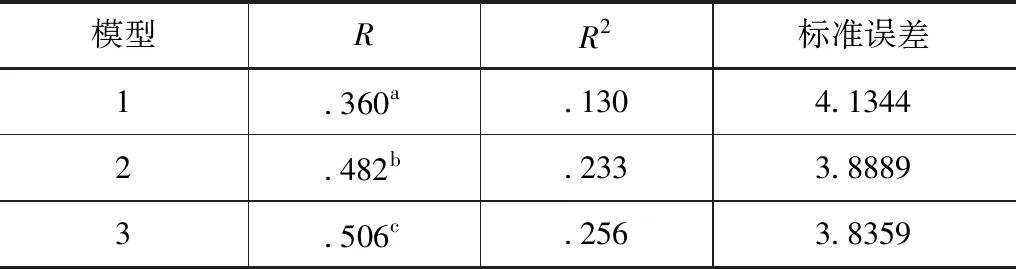
表5 回归模型摘要
模型1的预测变量是刀盘总推力;模型2的预测变量是刀盘总推力和刀盘转速;模型3的预测变量是刀盘总推力、刀盘转速和盾体铰接总力度。模型3的相关程度(R=0.506)及拟合程度(R2=0.256)均较高,掘进速度与刀盘总推力、刀盘转速和盾体铰接总力度间存在显著的非线性关系,第3种模型回归系数见表6。
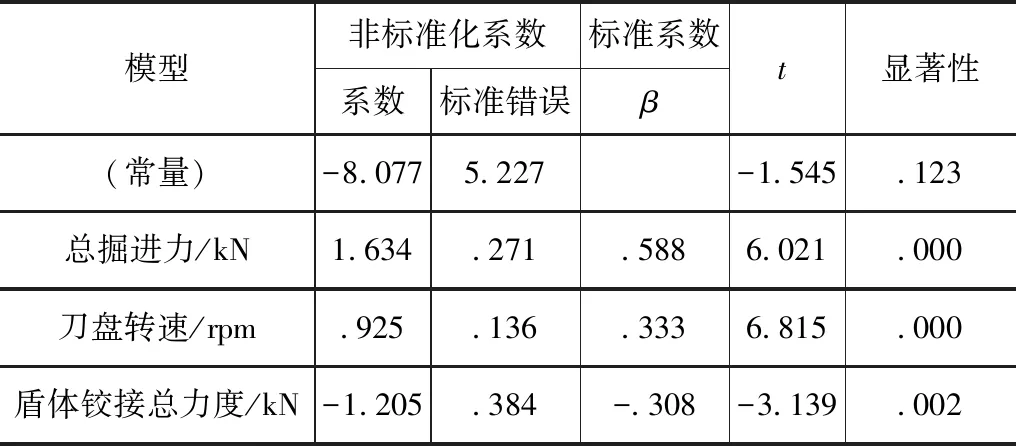
表6 掘进速度模型回归系数
拟合处理后的结果为:
y=-8.077+0.925y1+1.634y2-1.205y4
(6)
将y1、y2、y4代入(1)式整理,得到掘进速度数学模型为:
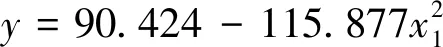
(7)
由式(7)得,刀盘总推力、刀盘转速和盾体铰接总力度是影响掘进速度的主要因素,由于刀盘扭矩的回归系数t检验结果不显著(P=0.797>0.05),所以刀盘扭矩对掘进速度的影响不予考虑;刀盘总推力、刀盘转速和盾体铰接总力度三者与掘进速度成比例关系,刀盘总推力对掘进速度的影响最大。
2.2 刀盘扭矩数学模型的建立与分析
刀盘扭矩是刀盘切削前方土体,所克服的全部阻力之和,单位为kN·m。刀盘扭矩为被动调节参数,反映刀盘切削土体的难易程度。
刀盘扭矩与刀盘转速:
(8)
刀盘扭矩与刀盘总推力:
T2=e1.020-9937.188/x2
(9)
刀盘扭矩与盾体铰接总力度:
T4=e1.196-9402.123/x4
(10)
刀盘扭矩与土仓压力:
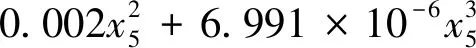
(11)
刀盘扭矩与掘进速度:
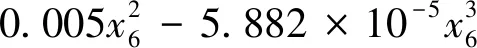
(12)
式中,x5—土仓压力;x6—掘进速度;Ti—各因素影响下的刀盘扭矩。
依托T1、T2、T4、T5、T6,采用“逐步”法拟合分析,得到3种模型摘要,见表7。
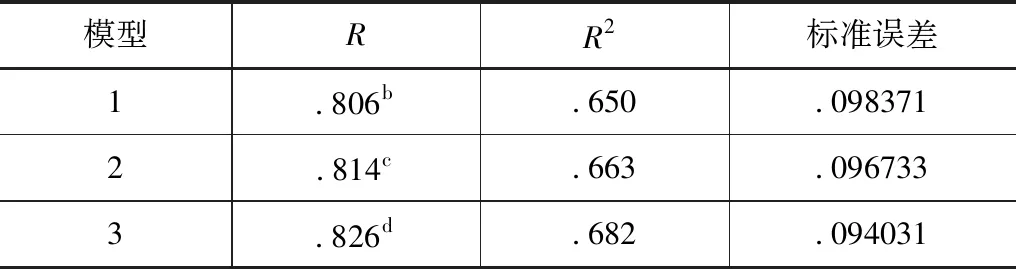
表7 刀盘扭矩回归模型摘要
模型1的预测变量为盾体铰接总力度和土仓压力;模型2的预测变量为盾体铰接总力度、土仓压力和刀盘总推力;模型3的预测变量为盾体铰接总力度、土仓压力、掘进速度和刀盘总推力。模型3的相关程度(R=0.826)及拟合程度(R2=0.682)均较高,盾体铰接总力度、土仓压力、掘进速度和刀盘总推力与刀盘扭矩间存在显著的非线性关系。
拟合处理后的结果为
T=0.22-0.507T2+1.09T4-0.013T5+0.214T6
(13)
将T2、T4、T5、T6代入(13)整理后结果为
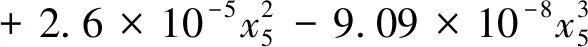
(14)
基于实测盾构机掘进数据,建立刀盘扭矩数学模型为式(14)。由于刀盘转速的回归系数t检验结果不显著(P=1.356>0.05),所以刀盘转速对刀盘扭矩的影响不予考虑;铰接总力度、掘进速度、刀盘总推力及土仓压力为刀盘扭矩的主要影响因素,刀盘总推力和盾体铰接总力度影响因子较大;刀盘总推力越大,盾体铰接总力度越小,刀盘扭矩就会随之减小。
3 掘进参数优化
掘进参数优化的意义在于土压平衡盾构机在复杂富水地层下掘进时,通过调整掘进参数,以达到最优盾构施工掘进速度,提高掘进效率保证工期。盾构机掘进速度的影响因素十分复杂,对掘进速度的控制需要通过调整盾体铰接总力度、刀盘转速和刀盘总推力等参数,最终在保证安全施工的前提下,达到最快掘进速度。因此以掘进速度数学模型为目标函数,盾体铰接总力度、刀盘转速及刀盘总推力为设计变量,建立有约束非线性规划数学模型如下:
(15)
本文采用局部优化法对掘进速度进行优化,将式(15)利用MATLAB软件编程。初值的设定对优化结果起到重要影响,所以设定初值为刀盘转速1.50r、刀盘总推力10237kN和盾体铰接总力度8587kN。
对掘进速度进行优化处理,优化结果见表8:

表8 优化结果
从表8可以看出,当调整盾体铰接总力度5000kN、刀盘转速为1.05r及刀盘总推力为25000kN时,该优化结果为掘进速度的最大值,该最大值为66.9mm/min,优化结果与盾构机在实际掘进过程中的掘进速度基本吻合,即证明了优化结果的正确性及可行性。在实际掘进过程中,可以根据所建立的数学模型,参考优化结果,合理调整掘进参数,使盾构机在复杂富水地层下获得较优的掘进速度,保证施工安全的同时提高掘进效率。
4 结论
本文通过分析掘进速度与刀盘扭矩和其他掘进参数之间的关系,得出以下结论:
(1)盾构机在富水、粘土及卵石地层下工作时,刀盘总推力和刀盘转速与掘进速度成正比,盾体铰接总力度与掘进速度成反比。复杂富水地层下刀盘扭矩对掘进速度的影响非常小,可忽略。刀盘总推力对掘进速度的影响最为明显,刀盘总推力越大,掘进速度越大。
(2)盾体铰接总力度、掘进速度、刀盘总推力和土仓压力为刀盘扭矩的主要影响因素,刀盘总推力越大、盾体铰接总力度越小,刀盘扭矩则越小。为提高刀盘寿命,应尽可能的减小刀盘扭矩。
(3)合理调整掘进参数以获得最优的掘进速度,在保证安全施工的同时提高工作效率,并对盾构机在复杂富水地层下掘进参数的设定具有理论指导意义,对盾构机寿命延长有一定的参考价值。
