盾构接收掘进中有限土体划分及土仓压力设定研究
2020-12-11刘军,陈达,韩旭,马烁
刘 军,陈 达,韩 旭,马 烁
(1.北京建筑大学土木与交通工程学院,北京 100044; 2.中国机械设备工程股份有限公司,北京 100055)
引言
随着城市地下轨道交通的发展,盾构法隧道施工的应用越来越广泛。盾构法施工过程中,土仓压力的设定是盾构施工设计的重要环节,合理的土仓压力在与开挖面水土压力相平衡的同时,能实现对周边土体的较小扰动,从而对地表沉降和周边建(构)筑物影响较小。关于土仓压力的设定方法已存在很多研究成果[1-4]。赵文等[5]详细比较了两种楔形体模型的开挖面支护压力,得到了较精确的简化计算公式。李潮[6]比较了常用的3种掌子面土压力计算模型,针对砂卵石地层给出理论建议。侯永茂等[7]根据对刀盘前土体挤压状态的分析,提出以变形控制为准则的土仓压力设定方法。杨永强[8]通过模型分析,指出土仓压力的设定值可根据土体性质和沉降要求设定在不同的土压力区间内。鞠鑫[9]、郑刚等[10]研究了土仓压力等掘进参数对地表沉降的影响。现有盾构土仓压力的研究主要集中在正常掘进阶段,根据朗肯土压力确定土仓压力大小,对于接收掘进阶段土仓压力的设定一般根据工程经验和监测数据,没有确定的理论模型,这也是盾构在接收阶段容易出现较多工程事故的重要原因。
盾构接收掘进阶段,由于围护结构的存在,开挖面前方土体不能满足朗肯土压力理论中半无限土体的假设。因此,对于接收阶段土压力的计算应采用有限土体的理论来分析。目前,有限土体土压力的研究主要集中在邻近建筑物的基坑工程中。马平等[11]、王洪亮等[12]在库伦土压力的基础上建立有限土体受力模型,提出有限土体中滑裂面破坏角的确定方法。刘冬[13]、王闫超等[14]利用不同模型得到有限土体中主动土压力的计算公式,并与朗肯土压力计算作对比分析。胡卫东等[15]、韩同春等[16]、应宏伟等[17]建立有限土体模型,在考虑围护结构摩擦力的条件下计算被动土压力值。马继才[18]根据有限土体实际受力状态得到土压力计算模型和临界宽高比修正模型。王磊[19]将有限土压力理论应用到异型基坑设计中,获得了良好的经济效益。黄鑫[20]根据主应力迹线分析了有限土挡墙上的土压力分布。杨明辉等[21]通过模型试验,研究了有限宽度的无黏性土在3种变位模式下的破坏规律和主动土压力值。万励等[22]通过离散元模拟,得到有限土体滑裂带倾角的变化规律。
在盾构接收掘进阶段,利用有限土压力理论计算开挖面前方土体受力的模型是符合实际状态的,目前这方面的研究还较少。通过建立有限土体模型,根据滑裂面理论确定了从半无限土体进入有限土体的界限位置,并按照控制土体扰动的原则给出了合理的土仓压力设定值,这一设定原则对控制地表沉降和围护结构变形均较有利,可为无障碍接收的工程安全提供保证。这一方法已在北京地铁16号线某区间盾构无障碍接收的工程中得到验证,可以为同类工程提供参考。
1 半无限土体到有限土体的划分界限
盾构正常掘进阶段,土仓压力和前方水土压力相平衡,以保证开挖面稳定。水土压力的计算多使用朗肯土压力的计算方法。这种方式可以降低对土体的扰动,对地面沉降的控制效果较好。随着盾构机的掘进,刀盘前方到盾构接收井之间的土体逐渐变小,前方土体不能满足半无限土体的假定。同时,朗肯土压力理论中计算的滑裂破坏面将穿过围护结构。因此,对于这一土体状态,需单独建立有限土体模型分析受力和破坏性质。
土体在复合应力状态下,某一部分土单元由于剪应力过大出现剪切破坏,随荷载的增加,最终形成连续的滑裂破坏面造成土体失稳。在破坏过程中,滑裂破坏面的位置是一个重要参数。对于开挖面前方的土体,假设土体为均质土,滑裂破坏面是一个平面。当土仓压力不足时,前方土体失稳,将在盾构刀盘下边缘到地表之间形成滑裂面。滑裂面上方土体滑移,引起地表沉降,会带来诸多工程事故。
当盾构前方土体进入有限土体状态时,滑裂破坏面顶端会与围护结构相交,且滑裂面面积和角度也将发生变化,对于土仓压力的设定来说,这种变化带来的影响是巨大的。因此,在这一阶段,需重新建立和实际状态相符的模型进行计算。基于这种分析,将滑裂破坏面和围护结构的位置关系,作为半无限土体到有限土体的分界标准。当滑裂面顶端恰好位于围护结构顶端时,土体将从半无限状态进入有限状态,绘制盾构即将进入有限土体时的示意,如图1所示。滑裂面与水平面的夹角为θ,在有限土体状态中,朗肯土压力的基本假定不成立,因此滑裂面倾角要采用新的方式来计算。取盾构恰好进入有限土体状态时,破坏面上方的土体受力分析,如图2(a)所示。
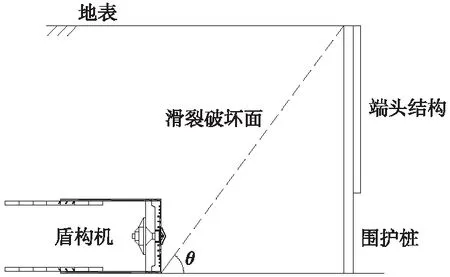
图1 盾构进入有限土体示意

图2 土体受力分析简图
地面到盾构机底端的垂直距离为z,刀盘位置到围护结构的水平距离为b,土体的重度为γ,黏聚力为c,内摩擦角为φ。为保证围护结构的安全,并遵循与盾构掘进的真实状态接近的原则,取上方滑动土体处于主动土压力的临界状态分析。滑动体ABCD每米宽度范围的重力W=γb(z-0.5btanθ),左侧受到盾构土仓压力的合力E作用。在滑裂面上存在下部土体对滑动体的支持力R,支持力方向和滑裂面法线方向的夹角为内摩擦角φ,滑裂面摩阻力K=bc/cosθ。该受力状态同时不考虑两侧土体和围护结构对有限土体的作用,把盾构扰动带来的有限土体受力变化交给土仓压力承担。将摩阻力K分解为水平和竖直两个方向,由于土体处于平衡状态,可得到封闭三角形如图2(b)所示,支持力R和竖直方向的夹角为θ-φ。根据力的三角形法则,土仓压力合力E的表达式为
E=[γb(z-0.5btanθ)-bctanθ]tan(θ-φ)-bc
(1)
当深度z、水平距离b和土体参数c、φ确定时,土仓压力合力E是关于θ的函数。根据极限平衡理论,当dE/dθ=0时,E取极值即为主动土压力合力值,此时角度θ即为滑裂面倾角。将土仓压力合力E对θ求导得
0.5γb2(1+tan2θ)tan(θ-φ)-
0.5γb2tanθ[1+tan2(θ-φ)]-
bc(1+tan2θ)tan(θ-φ)-
bctanθ[1+tan2(θ-φ)]
(2)
令dE/dθ=0,整理得滑裂破坏角θ的表达式
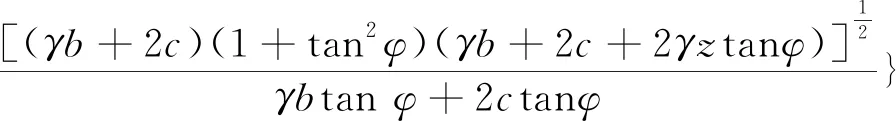
(3)
表达式中刀盘位置到围护结构的水平距离b是未知量。另外,当盾构机恰好进入有限土体时,由图2中的几何关系可知
θ≈arctan(z/b)
(4)
联立式(3)、式(4)两式,即可求得b值。当盾构掘进至刀盘前土体宽度为b时,采用有限土体极限平衡理论计算的滑裂破坏面将与围护结构相交,此时前方土体的水土压力不能再按照朗肯土压力来计算,土仓压力的设定要做出调整。盾构到达这一临界位置时,称前方土体由半无限状态变为有限状态,也即盾构施工由正常掘进阶段进入接收掘进阶段。这种方法可以对盾构前方土体所处的状态进行划分,从而合理地调整土仓压力等掘进参数,保障土体和围护结构安全。
2 有限土体中盾构土仓压力的设定
土压平衡盾构机掘进过程中,土仓压力的设定对于控制盾构施工对周围环境的影响意义重大。土仓压力设置过大或过小,都会对周围土体中存在的既有结构和地面上的建(构)筑物造成很大影响。[7]在盾构的无障碍接收过程中,这种影响更为严重。这是因为洞口处围护结构使用的玻璃纤维筋是脆性材料,且在接收井开挖过程中,围护结构已经产生朝向临空侧的变形,若土仓压力过大,可能会使围护结构变形过大,提前达到极限状态发生破坏,威胁人员和财产安全。
盾构正常掘进时,工程中以开挖面前方的静止土压力为依据,根据地层条件设定土仓压力。在接收掘进过程中,实际工程中主要根据经验或现场试推进的方法确定土仓压力的控制值,同时根据监测结果实时进行调整,这样的方法缺少理论支持,且特定工程的方法不具备推广使用的能力。另外,由于监测结果往往有时间上的滞后性,监测到的影响已经发生,无法提前预防。因此,关键还是要控制土仓压力的大小,以保持开挖面稳定。现有的研究表明,可根据地层状态和沉降要求选择土仓压力的设定范围,地层稳定性较好且地表沉降要求不高时,可设置土仓压力值介于主动土压力和静止土压力之间;地层稳定性较差或地表沉降要求较高时,可设置土仓压力为静止土压力值;地层稳定性较差且地表沉降要求较高时,可设置土仓压力略高于静止土压力值[8]。本文将按照这样的设定原则,结合有限土体的土压力理论,给出盾构接收掘进时有限土体中的土仓压力设定依据。
2.1 土仓压力的下限值
盾构土仓压力较小时,开挖面前方的土体产生朝向刀盘方向的微小位移,并在土体中形成滑裂面。开挖面前方土体为有限土体时,滑动土体截面呈梯形。根据库伦土压力的计算原理,对滑动土体进行受力分析,这与第一章中分析滑裂面倾角时的受力状态相同。因此,根据力的平衡三角形,得到土仓压力合力E的表达式(式(1)),根据极限平衡理论,将E对滑裂面倾角θ求导,当求导等于零时,得到滑裂面倾角θ的表达式(式(3))。从θ的表达式中可以看出,滑裂面倾角和土体参数有关,且和盾构机所处的位置有关。在开挖面前方土体进入有限土体状态后,前方土体宽度是已知量,因此,我们可以取接收阶段每环管片距围护结构的距离为不同的土体宽度b,将垂直距离z和土体宽度b代入式(3),求出盾构机到达各位置时前方土体的滑裂面倾角值。将倾角θ代入式(1),即可得到盾构机处于该位置时土仓压力合力E的大小,也就是有限土体主动土压力合力的大小,进而可以得到土仓压力值。
理想状况下,取土仓压力为有限土体主动土压力大小,可以最大程度减小盾构掘进对围护结构附加应力的影响,保证围护结构的强度和稳定性。但实际工程中由于各种未知因素的存在,结合盾构接收时对地表沉降的控制要求,可将主动土压力值作为土仓压力设定的下限,接收掘进过程中土仓压力的设定应高于主动土压力值。
2.2 土仓压力的参考值
盾构掘进必然会对周围土体产生影响,土体受到扰动之后土颗粒发生移动,重新排列到新的稳定状态。当土仓压力最接近原始地层应力状态时,盾构施工对土体的影响最小。因此正常掘进状态中,取库伦土压力理论的静止土压力作为土仓压力设定的依据。对于有限土体而言,静止土压力系数不再适用,需选定一个静止状态的受力情况作为依据,分析此时土仓压力合力的数值关系。为了尽可能减小对土体原有状态的扰动,选取土体仅受自身重力、滑裂面支持力和土仓压力合力的状态进行受力分析,如图3(a)所示。在该状态下,开挖面前方土体既无向前滑动的趋势,也无向后滑动的趋势,对地表沉降和围护桩受力的影响均较小。此时,有限土体重力为W,土仓压力合力为E,滑裂面上支持力为R。由于土体处于平衡状态,可得到封闭三角形如图3(b)所示,支持力R和竖直方向的夹角为θ-φ。

图3 静止状态下土体受力分析简图
根据力的三角形法则,土仓压力合力E的表达式为
E=[γb(z-0.5btanθ)]tan(θ-φ)
(5)
与主动土压力的计算同理,根据极限平衡理论,当dE/dθ=0时,E取极值,此时角度θ即为滑裂面倾角。将土仓压力合力E对θ求导得
0.5γb2(1+tan2θ)tan(θ-φ)-
0.5γb2tanθ[1+tan2(θ-φ)]
(6)
令dE/dθ=0,整理得滑裂面倾角θ的表达式
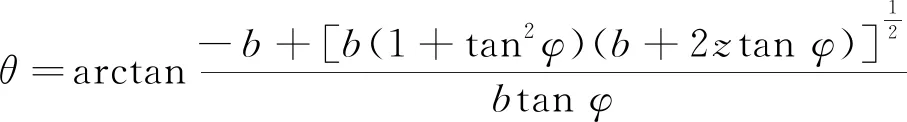
(7)
实际工程中,代入已知的参数b、z和内摩擦角φ,即可求出滑裂面倾角。将求出的滑裂面倾角代入式(5)中,即可求出土仓压力合力,进而求出土仓压力参考值。
2.3 土仓压力的上限值
土仓压力设置过大时,开挖面前方土体朝向接收井方向滑移,对接收井围护结构产生不利影响。此时围护结构的作用力不可忽略,可取围护结构对有限土体的作用力为被动土压力值[23],分析该极限平衡状态时的土体受力。与有限土主动土压力状态相比,滑裂面支持力和摩阻力的方向改变。在该状态下,土仓压力的合力与围护结构作用力、滑裂面摩阻力、支持力的水平分量相平衡,受力状态如图4(a)所示。若土仓压力的设定超过该值,滑裂面摩阻力、支持力的水平分量不足以与土仓压力合力相平衡,剩余的土仓压力将直接作用于围护结构,再叠加土体对围护结构的侧压力,洞口处围护结构的安全性无法得到保障。
有限土体重力为W,土仓压力合力为E,滑裂面上支持力为R,支持力方向和滑裂面法线方向的夹角为内摩擦角φ,围护结构对土体的合力为P,P=Kpγ(z-btanθ)。由于土体处于平衡状态,可得到封闭三角形如图4(b)所示,支持力R和竖直方向的夹角为θ+φ。

图4 被动状态下土体受力分析简图
则土仓压力合力E的表达式为
E=[γb(z-0.5btanθ)+bctanθ]tan(θ+φ)+
bc+Kpγ(z-btanθ)
(8)
与主动土压力的计算同理,根据极限平衡理论,当dE/dθ=0时,E取极值为被动土压力的合力值,此时角度θ即为滑裂面倾角。将土仓压力合力E对θ求导得
0.5γb2(1+tan2θ)tan(θ+φ)-
0.5γb2tanθ[1+tan2(θ+φ)]+
bc(1+tan2θ)tan(θ+φ)+
bctanθ[1+tan2(θ+φ)]-Kpγb(1+tan2θ)
(9)
从求导结果可以看出,在有限土体被动状态下,土仓压力合力E为关于θ为单调增函数,求导不存在等于零的θ值。有限土体被动土压力状态的滑裂面倾角和有限土体的宽高比有关,倾角大小随着土体宽高比的减小而增大,且增大趋势逐渐平缓,当有限土体宽高比小于1.5时,滑裂面倾角基本为一个稳定值[23]。针对盾构接收阶段而言,进入有限土体后土体宽高比即小于1.5,因此有限土体被动土压力状态的滑裂面倾角,可取一个固定值。根据其研究成果,当不考虑围护结构对土体的摩擦力时,可选择滑裂面倾角θ为45°-φ/2值,由此可将其他参数代入式(8)计算盾构机处于各位置时的土仓压力合力,进而求出土仓压力上限值。
3 实际工程验算
北京地铁16号线某盾构区间使用土压平衡盾构机,直径6 m,辐条式刀盘。管片为预制钢筋混凝土结构,环宽1.2 m。盾构埋深14 m,盾构穿越的土层主要为粉质黏土。具体的土层物理力学参数见表1。盾构接收端采用接收井进行无障碍接收,洞门范围内围护结构为玻璃纤维筋混凝土桩,其他范围内围护桩体为钢筋混凝土桩,钢筋和玻璃纤维筋做有效搭接,满足承载力要求。

表1 土层物理力学参数
对于计算用的土层参数,根据每个土层的厚度对土层的整体物理力学性质进行简化。取土体的重度为20 kN/m3,内摩擦角为24°,黏聚力为16 kPa。根据有限土体界限位置的确定方法,联立式(3)和式(4)可得,b=16.3 m时盾构前方土体进入有限土体状态,此时盾构机位于距洞口13~14环位置,前方有限土体的宽高比是0.815。针对该工程的盾构施工过程建立Flac3D模型,如图5所示。围护桩体的模拟监测结果显示在盾构机距洞口14环位置时,洞口处围护桩体的桩身弯矩开始受盾构掘进影响,如图6所示。这也说明从该位置开始,开挖面前方土体宽度不足,盾构机对土体的作用力将会沿有限土体传递到围护结构中。为保护围护结构安全,土仓压力不应再使用正常掘进的设定标准,应判断盾构进入有限土体,采用接收掘进的设定方式确定土仓压力。
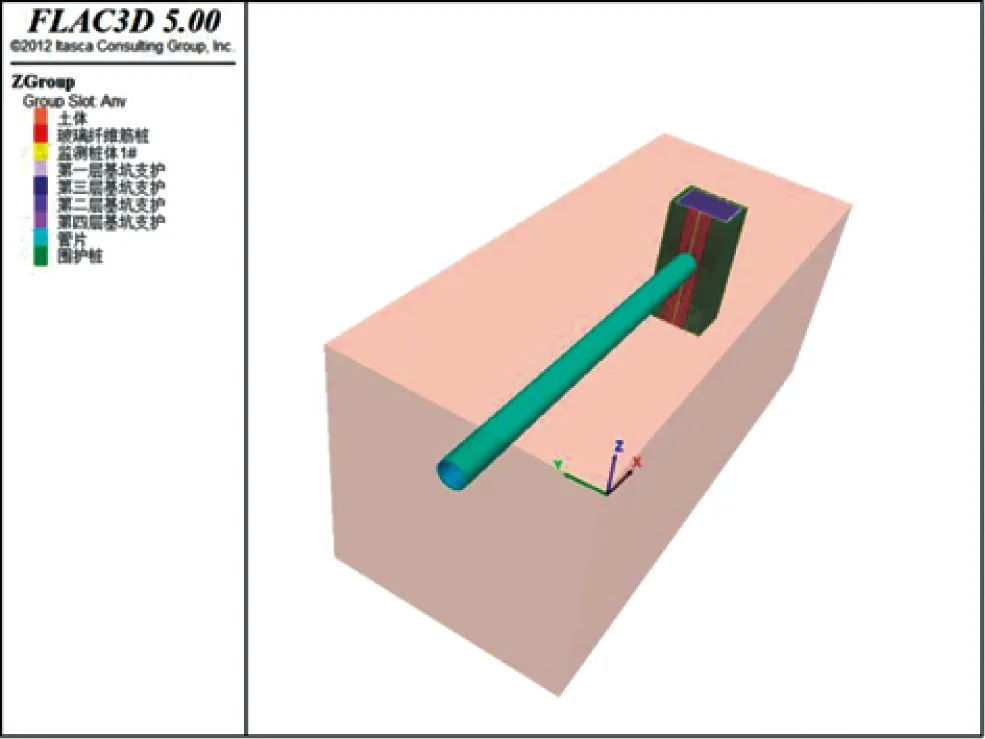
图5 盾构接收施工整体模型
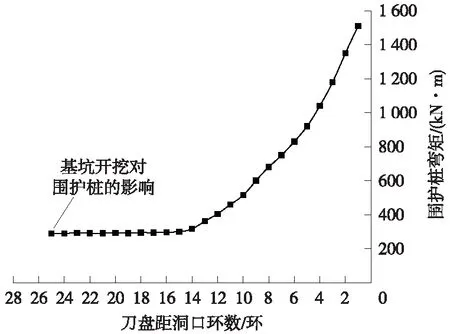
图6 围护桩弯矩模拟曲线
在盾构机进入有限土体状态时,根据有限土压力理论设定土仓压力,减小对围护桩的扰动。根据前述计算公式分别计算土仓压力设定的下限值、参考值和上限值,与工程实际的土仓压力设定相比较,如图7所示。从图7看出,理论计算结果与监测结果吻合较好,验证了理论公式的可行性。

图7 土仓压力计算与监测曲线
盾构机在距洞口14~6环位置时,实际土仓压力处于设定参考值和设定下限值之间,在6环之后,实际土仓压力基本处于设定下限值位置。基于有限土体被动土压力状态计算的设定上限值远大于其他值,这与正常掘进阶段被动土压力值的规律相同,设定土仓压力一般不会达到被动土压力值。设定上限值的大小随盾构机的掘进迅速下降,考虑不同土质状况对计算的影响,因此设定上限值的计算还是有必要进行的。该工程地质条件较好,且对地面沉降要求不高,因此选择土仓压力介于设定下限值和设定参考值之间是合理的,同时这也验证了理论计算的可行性。
盾构接收端现场设有3个断面对地表沉降进行监测,分别位于距离接收井3,8 m和15 m处,命名为DB-1、DB-2、DB-3,每个监测断面有7个监测点,监测点之间间距3 m,提取盾构机到达距洞口一环位置时的地表沉降,如图8所示。在Flac3D模型中,取土仓压力为计算参考值和下限值的平均值,得到地表沉降和围护结构变形的模拟值,并与工程现场的监测值相比较。如图9、图10所示。
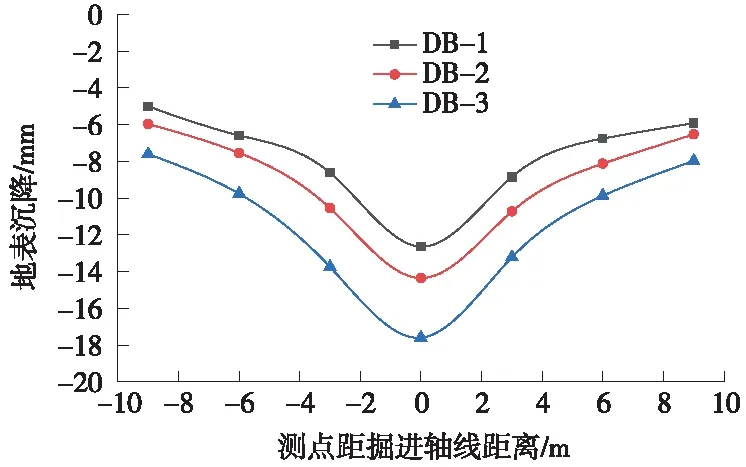
图8 地表沉降现场监测曲线
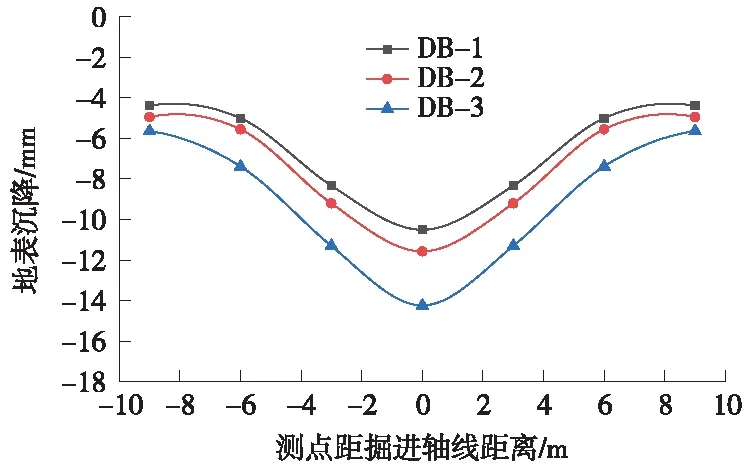
图9 地表沉降模拟曲线

图10 围护结构变形监测与模拟曲线
通过地表沉降和围护结构变形的监测、模拟图可以看出,采用有限土压力计算来设定土仓压力是有效的,地表沉降和围护结构变形都得到了较好的控制。
4 结论
结合有限土体土压力理论和土仓压力的设定原则,通过对有限土体极限平衡状态的分析,推导土仓压力设定的理论公式,并得到以下主要结论。
(1)开挖面前方土体由半无限状态到有限土体状态的划分界限,可按照有限土体的主动状态分析。取滑裂面顶端刚好处于围护结构顶端时盾构机所处的位置为界限位置。盾构机在该位置时前方土体由半无限状态变为有限土体状态,盾构掘进进入接收掘进阶段。
(2)盾构接收掘进阶段土仓压力的设定,可根据前方有限土体的实际状态分步计算,选择主动土压力状态计算设定下限值,选择特定的静止土压力状态计算设定参考值,选择被动土压力状态计算设定上限值。一般工程中可选择土仓压力位于设定下限值和参考值之间,对地表沉降和围护结构变形均有较好的控制作用。
根据北京地铁16号线某盾构工程实况,结合工程监测数据和数值模拟结果,验证了本文对盾构接收掘进阶段有限土体划分及土仓压力设定的理论分析是可行的,可为同类工程提供参考。
