地基与密肋复合墙结构动力相互作用测试分析*

2019-08-28卢俊龙

振动、测试与诊断 2019年4期

卢俊龙，张荫

(1.西安理工大学土木建筑工程学院西安，710048) (2.西安建筑科技大学土木工程学院西安，710055)

1 问题的引出

密肋复合墙结构是一种新型可装配式结构，适应我国建筑产业化及墙体改革的发展方向，其结构构造如图1所示[1]。在钢筋混凝土框格单元中填充砌块构成密肋复合墙板，砌块采用工业废料或农作物秸秆等制作，复合墙板通过连接柱、暗梁形成抗侧力构件，承担结构内力。密肋复合墙构造特殊，其动力计算及抗震设计方法与传统结构区别较大。

通过密肋复合墙结构的力学性能及简化计算模型研究，初步建立了结构抗震设计方法[2-4]。在此基础上，文献[5-6]建立密肋复合墙结构的恢复力模型，通过非平稳随机地震反应分析研究基于动力可靠度的设计方法。文献[7-8]等通过分析墙体承载特性及滞回性能，建立三道抗震防线量化设计方法。郭猛等[9-11]通过对比密肋复合墙结构和框剪结构的耗能性能，研究隐形框架与密肋复合墙的剪力分配关系。刘佩等[12]通过试验研究轻钢龙骨密肋复合墙结构的抗震性能。文献[13-14]通过1/6比例密肋复合墙结构振动台试验及数值模拟，研究结构动力特性、地震响应与破坏形态。

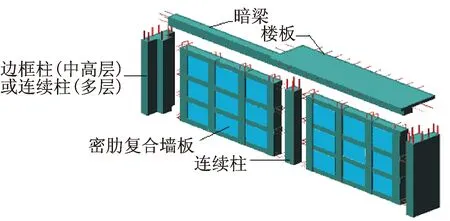
图1 密肋复合墙结构构造Fig.1 Constitute of multi-ribbed composite wall structure

因密肋复合墙结构抗震性能研究未考虑结构与地基动力相互作用的影响，相关结论存在局限性。为研究结构与地基的动力相互作用关系，易伟建等[15]考虑桩-土-结构相互作用，研究了脉冲型地震和常规地震作用下钢筋混凝土框架结构动力响应影响因素及规律。尚守平等[16]对比激振后刚性地基与设置土槽地基时钢框架模型的底部剪力，得到底部剪力折减系数。陈跃庆等[17]通过动力相互作用体系振动台模型试验，研究不同地基条件对相互作用的影响。

因密肋复合墙体力学性能、破坏模式均与传统结构区别较大，地震时与地基相互作用的规律较为复杂。为了研究二者动力相互作用关系，笔者设计制作了密肋复合墙结构模型及地基模型箱，分别进行刚性地基条件及相互作用条件下的振动台试验，分析结构动力响应的变化规律，研究密肋复合墙结构与地基动力相互作用及破坏机制，以完善密肋复合墙结构的抗震设计方法。

2 试件设计与制作

2.1 结构模型

以某大学7层密肋复合墙结构学生公寓为研究对象，原型结构为8度设防，Ⅱ类场地，黄土地基，底层结构高度为4.8 m，各层建筑层高均为3.0 m，建筑总高度为21 m，结构平面如图2所示。结构平面总尺寸为33.8 m×13.8 m，门窗洞口尺寸分别为900 mm×2 400 mm和1 500 mm×1 500 mm，密肋复合墙厚度为300 mm，楼板厚度为100 mm。该结构为平面规则结构，各开间单元横墙刚度及结构质量分布相同，因而各横向开间单元的动力特性与原结构接近。由于受到结构与地基相互作用系统中对结构模型尺寸的限制，故以1个横向子单元为对象来研究原结构的动力响应及破坏规律。

选取中间一榀代表性受力单元为原型结构(见图2阴影部分)，受到地基模型尺寸限制，几何相似系数设计为1/15，平面尺寸为0.54 m×0.45 m，总高度为1.52 m，采用质量配重满足质量相似，模型结构质量为212 kg，各层配重质量均为65 kg，总质量为0.97 t，复合墙体采用与原型材料类似的微粒混凝土，钢筋以镀锌铁丝模拟。主要控制参数的相似系数如表1所示。

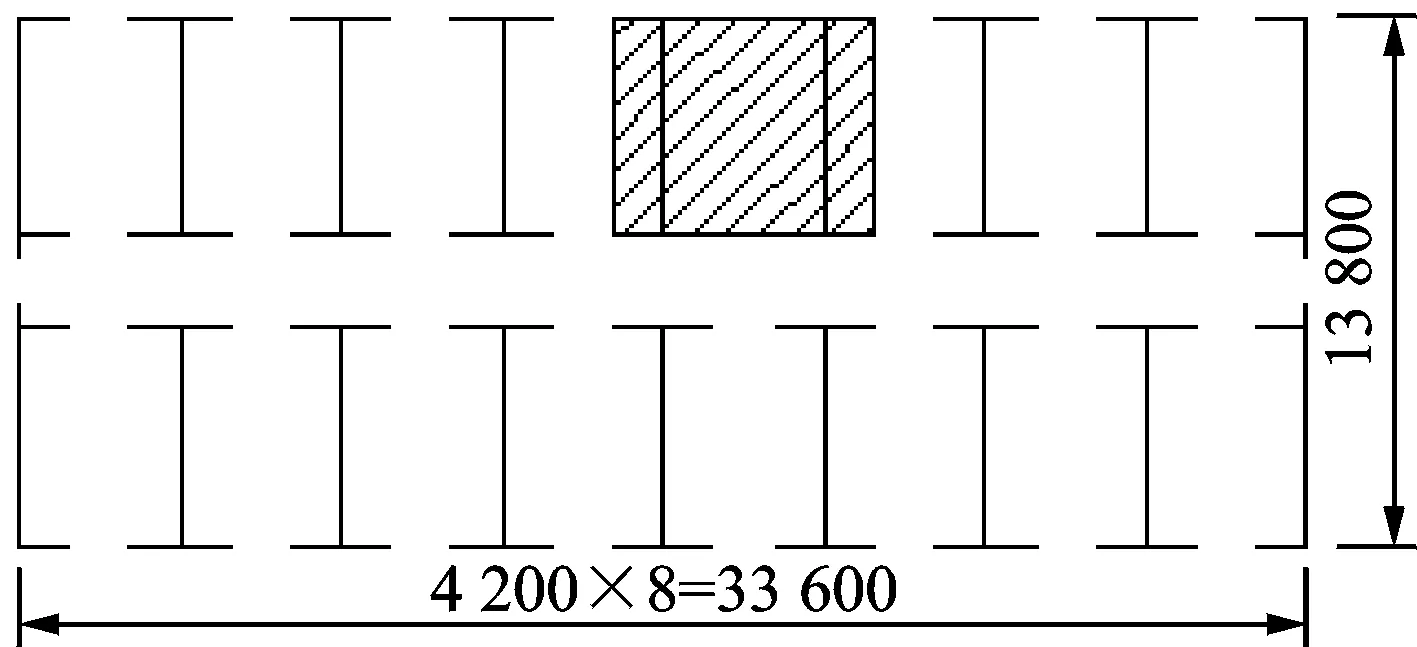
图2 原型结构平面(单位：mm)Fig.2 Plan of the structure(unit:mm)

按相似比条件设计的墙板厚度为20 mm，墙板肋梁及肋柱纵筋采用4根直径为1.2 mm的镀锌铁丝(4φ1.2)，箍筋直径为0.9 mm,间距为20 mm(φ0.9@20)，形成钢筋骨架后，将砌块按框格尺寸切割后置入，再浇筑细石混凝土制作墙体。在钢筋混凝土筏板基础浇筑完成后，将基础、墙体与楼板进行装配，完成模型制作，如图3所示。

表1 结构模型的相似系数Tab.1 Similitude coefficients of the model

图3 密肋复合墙结构模型Fig.3 Model of the multi-ribbed composite wall structure

2.2 地基模型

为了减小地基模型箱效应,控制结构模型的平面尺寸，应满足地基模型与结构模型的平面尺寸之比小于5[18]，因而地基土箱平面尺寸为2.56 m×2.93 m，高为2.1 m，采用6 mm厚的钢板制作。为防止钢板在土压力作用下产生过大变形而破坏，在钢板外部设置劲性钢梁。在箱体钢板内侧以环氧树脂胶粘贴5 cm厚的黏滞阻尼材料，模拟远场地基效应。在箱体底部铺设30 cm厚的卵石层模拟基岩层，然后将重塑黄土按分层25 cm进行夯实，地基土层总厚度为1.8 m。控制压实系数不低于0.85，含水量为19%左右，夯实后测得压缩模量为13.9 MPa，地基模型总质量为11.2 t。

2.3 相互作用系统模型

当地基土夯筑至基础底面设计标高时，将结构模型埋入土体并回填夯实，基础埋深为0.25 m，压实地面形成密肋复合墙结构与地基相互作用体系试验模型如图4所示。

图4 密肋复合墙结构与地基相互作用体系试验模型Fig.4 Model of interaction system of multi-ribbed wall structure and subsoil

3 试验概况

试验时，先进行密肋复合墙结构与地基相互作用系统的振动台试验，试验完成后结构基本完好，而后将上部结构模型嵌固于台面模拟刚性地基条件再进行振动台试验，通过两种工况对比，研究密肋复合墙结构与地基动力相互作用关系。

3.1 地震波输入

为了充分考虑场地地基条件及地震动输入对结构地震反应的影响，按烈度条件及相似比要求将地震波进行压缩与调幅，加速度峰值按7度、8度及9度递增，选用EL-Centro波(以下简称为EL波)及天津波(以下简称TJ波)，分别按单向水平、双向水平及三向加速度进行输入。

以结构纵向为地震作用主方向(x向)，单向输入时加速度峰值按相似比要求取值，双向水平输入时x向与y向(横向)峰值之比为1∶0.85，三向输入时x向、y向与z向(竖向)峰值之比为1∶0.85∶0.65。按试验设计要求，分别在刚性地基条件及考虑地基与结构相互作用条件下进行试验，按相应烈度输入地震波，其中x向的加速度峰值如表2所示。

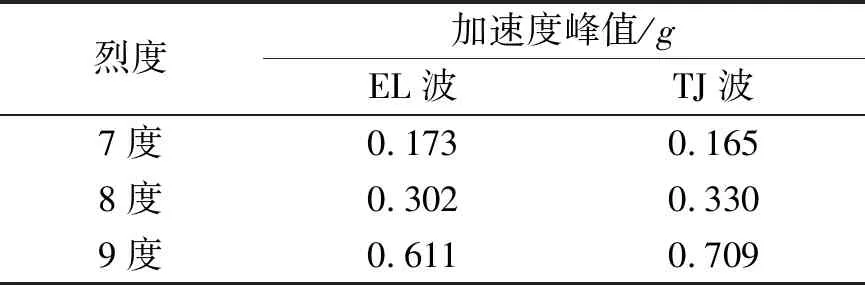
表2 不同烈度所对应的加速度峰值Tab.2 Peak value of acceleration at different intensify

3.2 测点布置

试验采集台面、地基表面(刚性地基时为基础顶面)及部分楼层的加速度及位移响应，测点布置如图5所示。在每个测点均沿x向、y向及z向布置位移与加速度传感器各1个，加速度传感器采用ICP压电式传感器，位移传感器采用891-Ⅱ型超低频动态传感器。

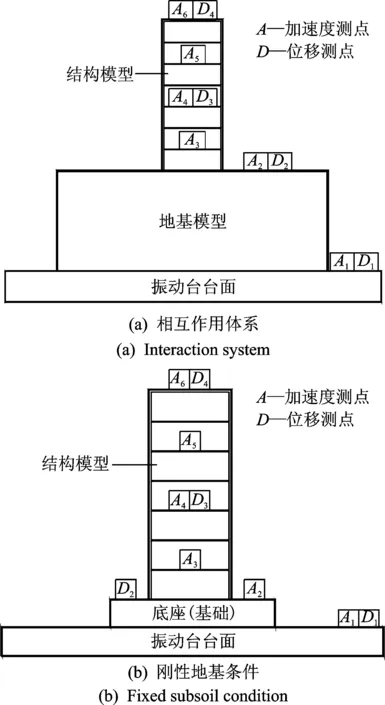
图5 测点布置示意图Fig.5 Location of test sensors

地基表面传感器安装在埋置土体中的水泥砖表面，保持砖表面水平，在其表面粘接毛玻璃片和薄钢板，将位移传感器粘接毛玻璃片，加速度传感器吸附于薄钢板上，如图6所示。各楼层传感器采用同样的方法安装在楼面，使传感器与测点同步运动。

图6 传感器安装Fig.6 Installation of sensors

4 试验现象

4.1 地基破坏

地基对地震波具有放大效应，地基土具有阻尼效应，可吸收大部分振动能量，因而进行相互作用体系试验时上部结构基本完好，破坏现象为地基土开裂，随着烈度愈高，开裂愈显著，具体破坏过程如下。

为满足连续加载的要求，裂缝观测均在按各烈度三向EL波加载完成后进行。对比图7和图8可以发现，完成7度EL波加载后，地基沿结构首层底部四周开裂，进而沿纵向与横向往两边延伸(图8中蓝色线)，裂缝宽度约为0.5 mm，纵向裂缝长度约为结构纵向宽度，横向裂缝开展至土箱内边缘。

图7 试验前地基土表面Fig.7 Subsoil surface before test

图8 7度后地基土表面裂缝Fig.8 Cracks of subsoil surface under 7 degree

完成8度三向EL波加载后的裂缝开展如图9所示，原裂缝宽度增大并继续延伸，出现与原裂缝平行的新裂缝，且在原裂缝周围产生宽度较小的支裂缝，新出现裂缝如图9中的黄色线所示。

图9 8度后地基土表面裂缝Fig.9 Crack of subsoil surface under 8 degree

当烈度提高至9度后，结构四周土体的裂缝均延伸至地基外边缘，且宽度显著增加，如图10所示。基础四周裂缝宽度最大，约为2 mm左右，同时沿每条主裂缝上又出现了多条支线裂缝，如图10中红色线条所示，但支线裂缝宽度较小，另外在结构四周新出现了部分裂缝，其长度与宽度均较小。

图10 9度后地基土表面裂缝Fig.10 Crack of subsoil surface under 9 degree

在加载过程中，上部结构位移响应明显，结构楼层水平位移及转动直接可见。

4.2 结构破坏

相互作用条件下的所有加载工况完成后，密肋复合墙结构模型仍保持完好，在刚性地基条件下输入9度地震波时，结构发生破坏，具体如下。

当输入7度及8度地震波时，结构模型中各楼层墙板及楼板基本完好，无裂缝出现。当输入烈度达到9度时，结构首层及第2层窗洞边缘出现部分纵向细小裂缝，如图11(a)所示，且首层横墙方向也出现部分裂缝。按9度继续加载，首层底部墙板与筏板间局部脱离，如图11(b)所示，结构有明显的水平滑移，随即停止加载。

图11 上部结构裂缝Fig.11 Cracks of the structure

4.3 破坏机制

由试验现象可见，地震作用下密肋复合墙结构与地基相互作用系统的破坏形式主要为地基开裂。由于相似比条件制约，基础埋深较小，夯土地基对结构的嵌固作用有限，因此成为相互作用体系的薄弱部位。因地基土具有阻尼效应，可通过开裂变形耗散部分振动能量，从而避免上部结构发生破坏。

在刚性地基条件下，结构模型高宽比较小，刚性较大，当输入地震烈度较低时结构响应不明显，不能形成薄弱部位。当烈度较高时，结构底部剪力增大，与基础连接强度不足而发生破坏，导致结构失效。

地基模型质量与结构模型质量比为11.5，输入地震波后地基与结构的相对运动可耗散地震能量，具有一定的阻尼减震作用。在刚性地基条件下，地震能量全部由结构吸收，结构破坏较为严重。可见，地基与结构相互作用对结构破坏模式影响显著，地基的阻尼及动力放大效应对结构地震响应也有一定影响。

5 相互作用分析

在相互作用体系中，结构水平位移响应由基础平动、基础转动及结构变形3部分组成。由于结构模型刚度较大，变形较小，因而输入地震波时结构响应由基础运动产生。在刚性地基条件下，基础固定于台面，结构位移响应由结构变形产生。通过比较地基表面与振动台面的动力响应可得到地基的放大效应，对比两种地基条件下结构楼层的动力相互作用效应。结合试验结果，定义地基放大效应系数ηs为

(1)

其中：Rs为地基表面的响应峰值；R0为振动台面的响应峰值。

定义相互作用效应系数Ii为

(2)

其中：Ri为相互作用条件下的响应峰值；Rr为刚性地基条件下的响应峰值。

5.1 地基放大效应

按式(1)计算各不同烈度及地震波输入方式时地基对水平x向加速度放大效应系数，得到放大效应曲线如图12所示。地基对x向加速度的放大效应与烈度、地震波及输入方式均有关系。输入EL波时，在单向、双向及三向输入时，加速度放大效应系数均随烈度的提高而增大，单向与双向输入时随烈度基本呈线性关系，且单向输入时的放大系数略小于双向输入时。在三向输入时，烈度较低时放大系数亦较小，随着烈度提高至8度后，放大系数显著增大，9度时的放大系数大于单向及双向输入时的值。可见，多向地震作用的耦合效应亦对放大效应有一定影响。

同时发现，在天津波作用下，地基放大效应随烈度的变化规律与EL波不同，在单向及双向输入烈度为8度时放大系数最小，而当三向输入8度时的放大系数最大，且不同烈度时放大效应系数较为接近。由图13可见，试验输入的地震波频谱特性有一定区别。其中:天津波的峰值激励频段为2～6 Hz,位于其他频段的峰值均较小；而EL波峰值激励频段位于2～4 Hz，7～10 Hz两个区间；EL波的激励为双频段；天津波的激励为单宽频带。

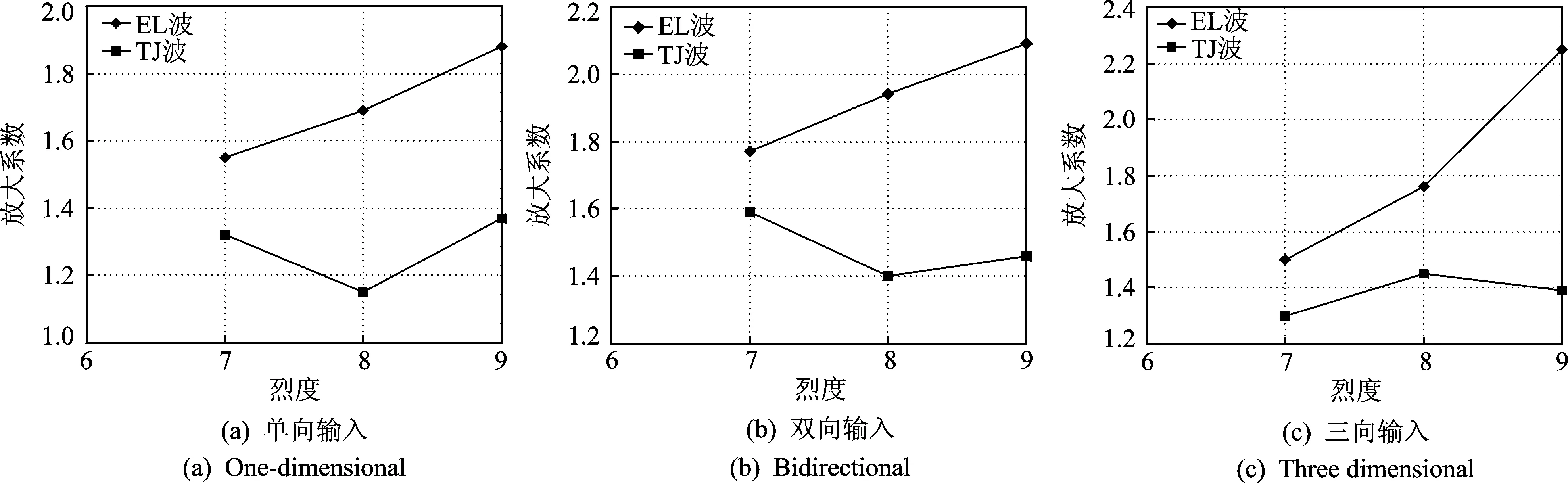
图12 地基放大效应系数Fig.12 Coefficient of amplify effect of subsoil

图13 输入地震波的频谱曲线Fig.13 Spectrum curve of the earthquake wave

图14 白噪声激励下地基的频域响应曲线Fig.14 Response curve of the subsoil affected by White Noise wave in frequency domain

依据白噪声扫频试验结果，对地基表面测点进行快速傅里叶变换得到频域响应曲线如图14所示。地基模型在加载前对0.5～3 Hz频段激励的响应显著，加载后地基频响曲线略有变化，其中在7度加载完成后的频响曲线变化较明显，如图14(b)所示。因振动加载导致地基土密实，地基频率略有提高。继续提高烈度加载完成后，地基的响应曲线变化不大，如图14(c)和图14(d)所示,且与加载前的响应曲线较为接近，其原因为烈度增加后，地基土开裂严重，振动导致地基土的密实效应也随之减弱。

比较图13与图14可知，按不同烈度地震波加载后地基频率变化范围位于天津波的峰值激励频段范围内，地基动力响应随输入地震动的强度变化较大，因而在不同烈度下地基的动力放大效应变化较大。

5.2 相互作用效应

通过式(2)计算各工况条件下各结构楼层测点的水平x向加速度的相互作用放大系数，以此比较分析相互作用效应与楼层及地震动输入的关系。

当按7度输入地震波时，由图15可见，输入EL波时的相互作用效应均较输入天津波时显著。当输入单向及双向EL波时，相互作用效应系数随测点高度的变化规律基本一致，最大值位于第5层，在顶层时减小，且单向输入时顶层的值最小，相互作用衰减了结构顶部的加速度响应，表现出减震效应，而在其他测点均对加速度具有放大效应。同时，EL波与天津波作用下的相互作用效应值除顶层外，其他楼层均相差较大。分析其原因在于，加载时先输入烈度较小的EL波，地基开裂不明显，结构与地基相对运动较小，完成EL波加载后输入天津波，地基开裂严重，振动时结构相对地基运动较为剧烈，二者相互作用的模式与输入EL波时有一定区别，故在两个工况下各楼层的相互作用效应系数相差较大。在三向地震作用下，输入EL波时的相互作用效应值略大于输入天津波时的值，曲线沿楼层高度方向的变化规律基本一致，输入EL波时3层以上各测点的效应值较为接近，而输入天津波时，5层以下各测点的效应值基本接近，表明烈度较小时，三向输入不同地震波时相互作用效应随楼层高度的变化规律基本一致。

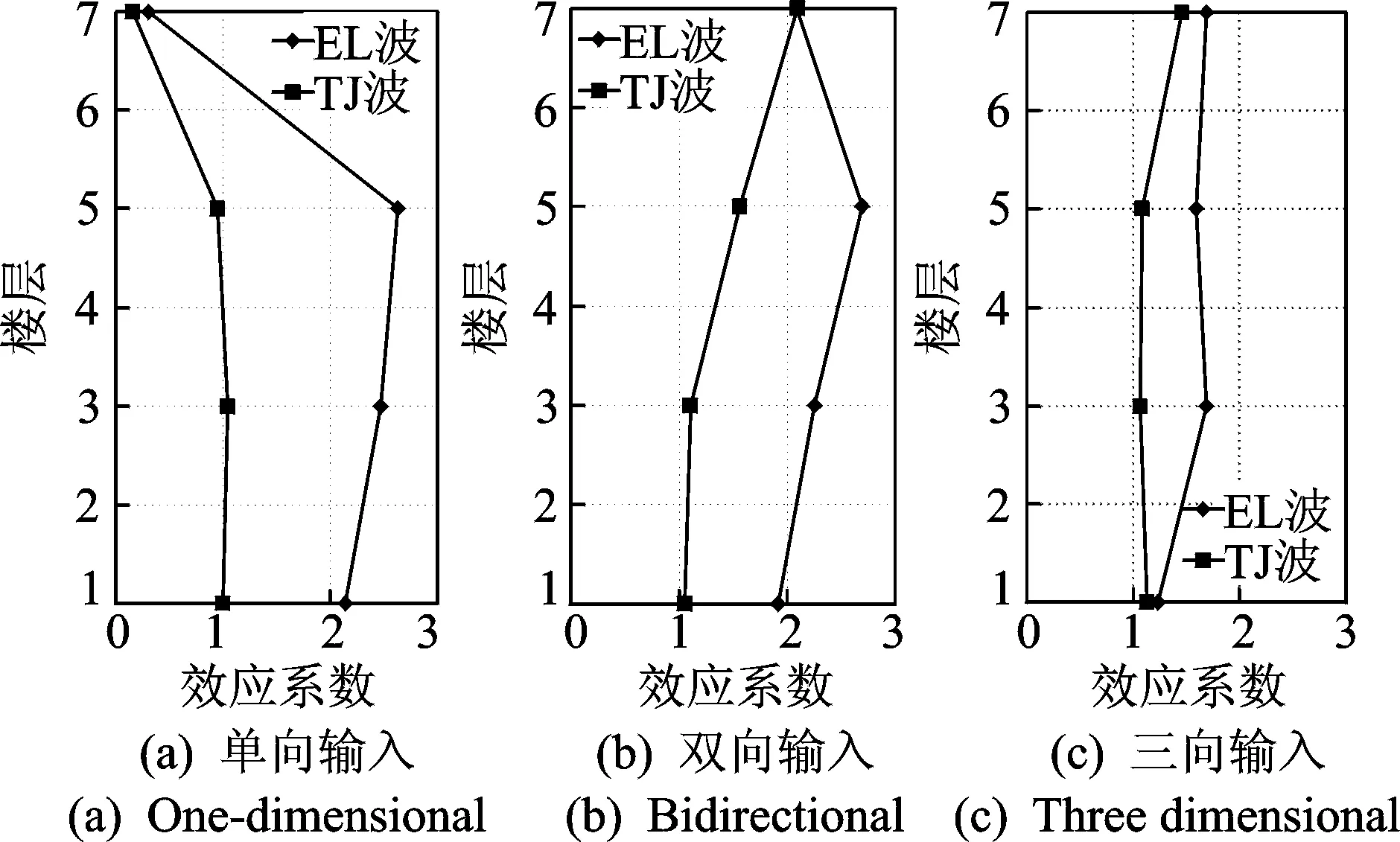
图15 7度时相互作用加速度效应系数Fig.15 Acceleration coefficient of interaction effect under 7 degree

当烈度提高至8度时，各工况条件下加速度相互作用效应随测点高度的变化规律较为接近。由图16可见，各工况条件下1层顶测点的相互作用效应系数值均接近于1，且单向输入两种波时，相互作用效应随测点高度的变化规律与7度时一致，在5层最显著，7层最弱。当输入双向及三向地震波时，顶层的相互作用效应均较为显著，且两种工况下各测点的相互作用效应系数值较为接近。

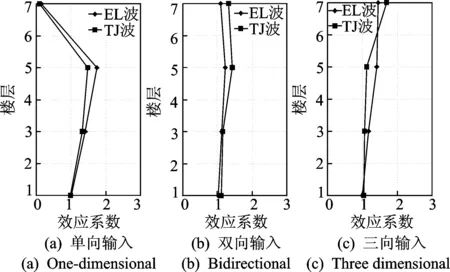
图16 8度时相互作用加速度效应系数Fig.16 Acceleration coefficient of interaction effect under 7 degree

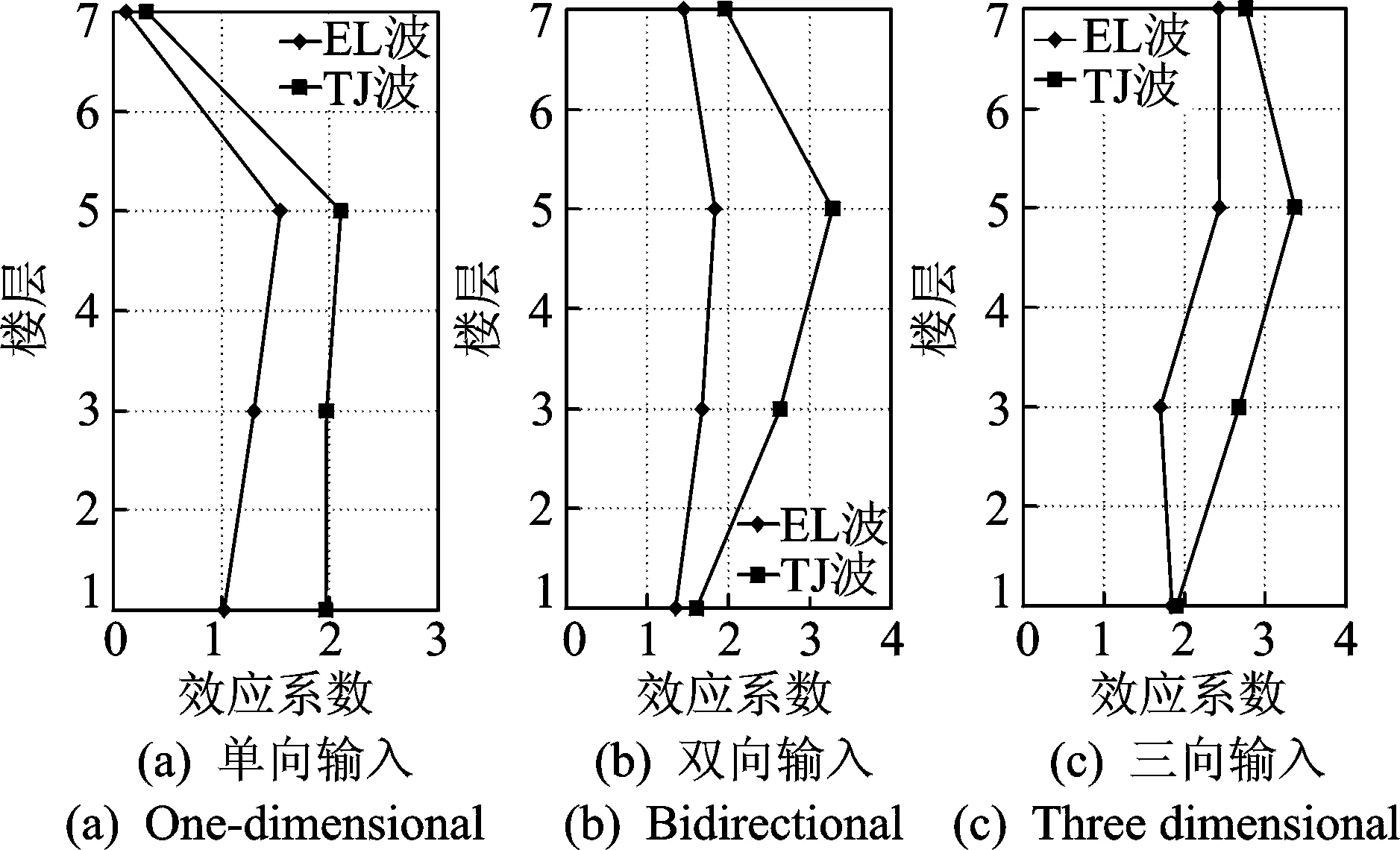
图17 9度时相互作用加速度效应系数Fig.17 Acceleration coefficient of interaction effect under 9 degree

由9度时相互作用加速度效应系数随测点高度的变化曲线可知，输入两种地震波时相互作用效应系数随测点高度的变化规律一致，但各测点对应的数值相差较大，如图17所示。单向输入两种不同地震波时，1层顶的效应系数相差较大，随测点高度的变化规律相同，7层顶的相互作用效应值均接近于0。双向及三向输入时，相互作用效应系数随测点高度的变化规律与单向输入时相同，但5层测点在输入天津波时的效应值均大于EL波，而到7层顶时，输入两种波时的相互作用效应又较为接近。同时可见，三向输入时首层顶的相互作用效应值接近，随测点高度的变化规律与7度及8度时相同，但各测点的效应值显著大于7度及8度输入时的值。

综合各工况加速度响应的相互作用效应曲线可以发现:当烈度为7度时，输入EL波时的相互作用效应值均大于输入天津波时的值；烈度为8度时，二者较为接近;当烈度为9度时，输入EL波与输入天津波时效应值的大小关系与7度时恰好相反。可见，结构顶部楼层测点的加速度响应受相互作用的影响较为显著。

5.3 相互作用机制

通过地基放大效应分析可见，各工况条件下地基对振动台面输入的加速度均具有放大效应，但放大后的地震动作用于模型结构时，各楼层动力响应与刚性地基条件时直接输入地震波时相比并非全部被放大。

结合试验加载过程及现象可以看出，因EL波适用于较硬场地土且在试验中首先输入该条波，当烈度较小时，地基尚未开裂，结构与地基相互作用系统的自振频率较高，地基对EL波的放大效应显著，相互作用对结构加速度及位移响应均具有放大效应。当EL加载完成后，地基开裂较多，结构与地基相互作用系统的自振频率随之降低，当输入地震波峰值较小时，相互作用对结构动力响应的放大效应不明显，当地震波峰值增加后，地基开裂后的阻尼增大，使相互作用体系的自振频率降低，相互作用对结构动力响应的放大效应随之显著。

通过对比地基放大效应与相互作用效应的最大值可以发现，各工况条件下地基放大效应系数的最大值为2.25，加速度相互作用效应系数的最大值为3.37。因此，对多层密肋复合墙结构进行抗震计算时，可依据地基对地震作用的放大系数确定考虑相互作用后的地震作用效应调整系数。