双胞铝合金管弯曲响应研究
2019-08-28邓中杰茅云生周晋阳黄治新
邓中杰 茅云生 袁 露 周晋阳 黄治新
(武汉理工大学交通学院1) 武汉 430063) (华中科技大学土木工程与力学学院2) 武汉 430074)
0 引 言
铝合金具有密度低,比模量大、比强度高等优良特性,因此,在汽车、船舶、航天等工程领域,铝合金薄壁结构被广泛用作能量吸收装置.弯曲破坏是薄壁结构在横向载荷作用下的一种典型的变形失效模式.国内外学者对薄壁结构在横向载荷作用下的弯曲响应进行了大量研究.Chen[1]开展泡沫填充管的弯曲试验,发现压头尺寸和泡沫长度对结构的变形过程有显著影响.Zhang等[2]研究了铝合金管在准静态和动态载荷下的弯曲响应,材料强度和载荷形式影响结构的变形模式.Crupi等[3]分析了蜂窝填充管的弯曲过程,结构的变形模式与跨距相关.这些研究结果表明,薄壁结构的弯曲特性受截面尺寸、载荷形式,以及边界条件等因素的影响.
近年来,为提高结构的能量吸收效率,多胞薄壁结构吸能特性和优化设计受到了广泛关注.Tran等[4]研究了横向载荷作用下,三角形和矩形多胞管的变形模式,并提出了理论模型,预测力的响应.Yin等[5]对泡沫填充多胞管横向冲击载荷作用下的吸能效率进行了优化设计.Hou等[6]分析了铝合金多胞方管在轴向载荷作用下的吸能特性,并基于响应面法对截面壁厚进行了优化设计.这些研究表明,多胞比单胞结构具备更好的吸能效率,截面变厚度优化设计能有效提高结构的能量吸收效率.但是,横向载荷下,不同几何参数对多胞管变形特征的影响还不清楚,而且关于多胞管截面变厚度优化的研究较少.
文中对双胞铝合金管在三点弯曲载荷下的变形特征和能量吸收特性进行了研究.运用有限元软件LS_DYNA分析了截面尺寸、压头半径、支承跨距、摩擦因数和载荷形式对双胞管变形模式、接触力以及能量吸收效率的影响.采用响应面法对多胞截面进行变壁厚优化设计,提高结构的能量吸收效率.
1 数值方法验证
参照文献[7],运用有限元软件LS_DYNA模拟单胞铝合金矩形管的弯曲过程,验证数值方法的正确性.图1为材料的工程应力-应变曲线,主要力学参数如下:密度ρ=2.7 g/cm3,弹性模量E=68 GPa,泊松比υ=0.33,屈服强度σ0=30.5 MPa,极限强度σu=90.5 MPa.铝合金试样的几何尺寸:长度L=250 mm、宽度a=30 mm、高度b=30 mm、厚度t=2 mm.图2为三点弯曲试验的示意图,压头和支承的直径D=10 mm,跨距s=200 mm,准静态加载速度为0.5 mm/s.

图1 AA1100-O工程应力应变曲线

图2 三点弯曲试验示意图
三点弯曲试验的有限元模型见图3.铝合金管采用实体单元建模,管壁厚度方向上划分三层网格,中间区域细化网格尺寸为1 mm,远离中间区域的网格尺寸为4 mm.根据LS_DYNA手册[8],铝合金材料采用Mat 24分段线性塑性材料模型,压头和支承采用Mat 20刚体材料模型;管壁和压头、支承之间相互作用采用面面接触模拟,方管设置自接触防止单元穿透,摩擦因数设置为0.3.
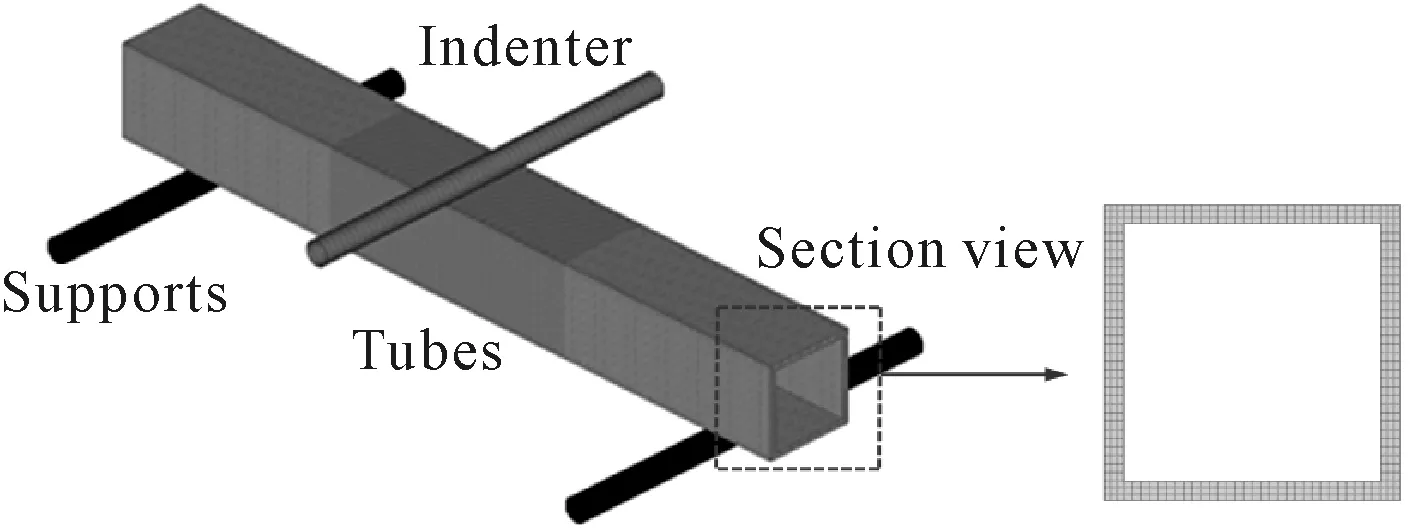
图3 三点弯曲试验的有限元模型
试验和数值结果的对比见图4.数值模拟的力-位移曲线、结构变形模式与实验结果吻合.有限元模型可以准确模拟出铝合金管三点弯曲载荷下的变形特征和接触力的响应.
2 双胞铝合金管的弯曲响应分析
2.1 截面尺寸的影响
图5为双胞管的示意图,表1为12组双胞管的截面尺寸,长度L=250 mm,压头半径R=5 mm,跨距s=200 mm,摩擦因数f=0.3,加载位移δ=45 mm.
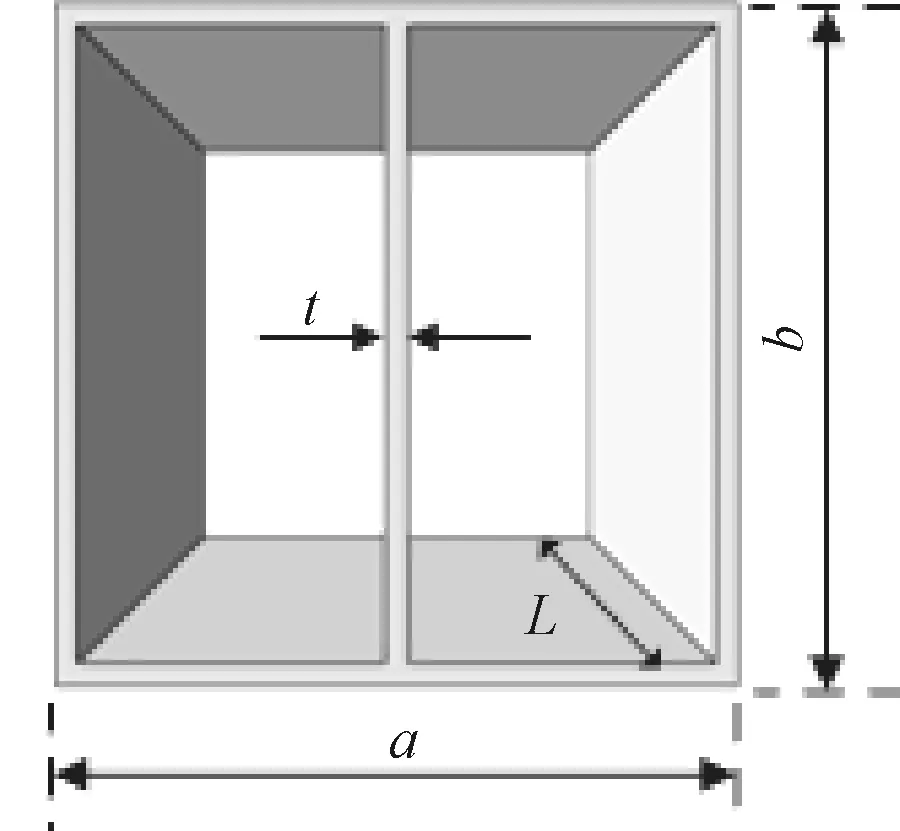
图5 双胞管的结构示意图
注:L-管长;a-宽度;b-高度;t-壁厚

表1 双胞管截面尺寸 mm
在加载位移δ=45 mm时,双胞管的变形模式见图6.
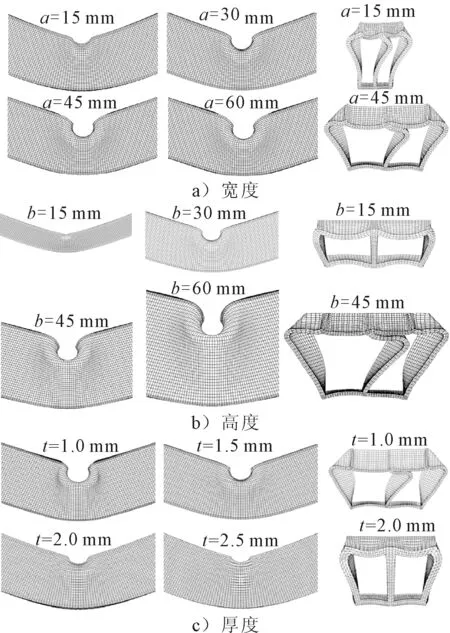
图6 不同截面参数的双胞管变形模式
变形特征包括:弯曲和局部凹陷.截面参数对凹陷程度有显著影响:截面宽度和高度增加,局部凹陷加深;管壁厚度增加,凹陷程度减小.这是由于双胞管的凹陷过程受到面板和腹板屈曲的共同影响.截面宽度增加,腹板的边界约束减弱;截面高度增加,腹板稳定性降低,容易发生欧拉屈曲;因此,管壁受挤压区域更容易发生凹陷.随着厚度增加,截面发生屈曲的临界应力增加[9],受挤压区域更难发生变形,凹陷程度减小.
由于接触区域凹陷程度不同,截面变形特征也存在差别,见图6.由图6可知,面板向下凹陷,腹板向外凸出;中间腹板比两侧腹板的弯曲程度小.这说明在变形过程中,面板、中间腹板和两侧腹板吸收的能量不同.
双胞管变形过程的力-位移曲线见图7.由于变形特征不同,力-位移曲线呈现不同的趋势.宽度(a=15 mm)和高度(b=15 mm)较小,厚度较大(t≥2.0 mm)的截面,在载荷作用下,凹陷程度较小,接触力先上升,再逐渐达到平稳.截面宽度、高度较大,厚度较小的双胞结构,接触力上升达到峰值,再出现下降,最后趋于平稳.

图7 不同截面参数的双胞管的力-位移曲线
2.2 压头半径的影响
压头尺寸会对双胞管变形过程产生影响,本节分析了压头半径R为5,10,15和20 mm的准静态加载条件下,双胞管的弯曲响应.结构几何参数:L=250 mm,a=30 mm,b=30 mm,t=1.5 mm.支承跨距s=200 mm,摩擦因数f=0.3,加载位移δ=45 mm.
双胞管的变形模式见图8,变形过程的力-位移曲线见图9.
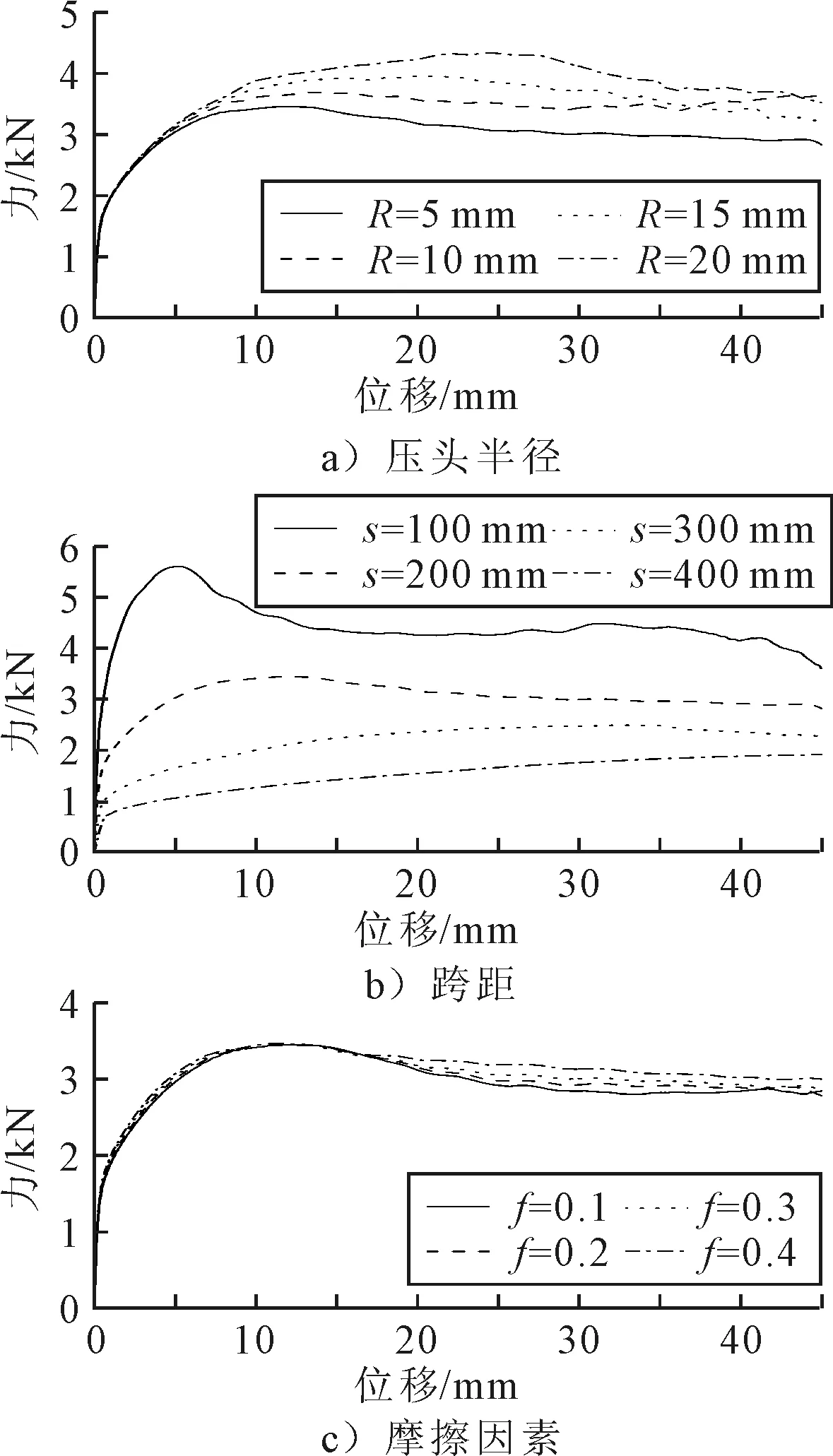
图9 不同载荷条件对力-位移曲线的影响
由图8a)可知,压头半径增加,截面凹陷逐渐变浅.这是由于压头尺寸增大,管壁与压头的接触面积增加,从而避免塑性变形集中在局部区域.由图9a)可知,接触力显著增加,再逐渐趋于平稳;压头尺寸增加,接触力逐渐增大.
2.3 跨距的影响
为研究跨距对双胞管弯曲响应的影响,分析跨距s为100,200,300和400 mm的准静态加载条件下,结构的变形过程.几何参数:a=30 mm,b=30 mm,t=1.5 mm,L=500 mm.压头半径R=5 mm,摩擦因数f=0.3,加载位移δ=45 mm.
由图8b)可知,随着跨距的增加,变形模式由弯曲和凹陷逐渐转变为弯曲.跨距s=100 mm时,压头压缩进管内,腹板向外凸出明显.随着跨距增加,局部凹陷逐渐变浅,跨距s=400 mm时,接触区域几乎不会凹陷,只产生弯曲变形.这是由于随着跨距增加,结构受到支承的约束减弱,更容易发生弯曲变形.由图9b)可知,接触力先逐渐增加,再逐渐趋于平稳;随着跨距增加,接触力逐渐减小.
2.4 摩擦系数的影响
管壁与压头、支撑之间的摩擦会对结构弯曲响应产生影响,数值模拟分析摩擦因数f为0.1,0.2,0.3和0.4的准静态加载条件下,双胞管弯曲过程.几何参数为L=250 mm,a=30 mm,b=30 mm,t=1.5 mm.压头半径R=5 mm,跨距s=200 mm,加载位移δ=45 mm.
由图8c)可知,不同摩擦因数条件下,双胞管的变形特征基本相同,结构发生弯曲,接触区域产生相同程度的凹陷.由图9c)可知,在峰值之前,摩擦因数对接触力无影响;峰值之后,随着摩擦因素增加,接触力逐渐增大.
2.5 动态和静态三点弯曲比较
由于碰撞过程中,结构变形和能量吸收都发生在动态载荷作用下.为了研究动态载荷作用下,双胞管的弯曲响应,分析三种不同加载速度:v=5,10,15 m/s时,双胞管的变形模式和力-位移曲线特征,并且与准静态的响应特征进行对比.双胞管的几何参数:L=250 mm,a=30 mm,b=30 mm,t=1.5 mm.支承跨距s=200 mm,压头半径R=5 mm,摩擦因数f=0.3,加载位移δ=45 mm.由于铝合金是应变率不敏感材料,数值模拟不考虑材料的应变率效应.
双胞管在动态和准静态载荷作用下的变形模式基本相同,因此,没有给出结构的变形特征图.在加载过程中力-位移曲线见图10,曲线可以分为两个阶段:波动阶段和稳定阶段.动态载荷作用下,力-位移曲线在初始阶段出现了较高的峰值,再逐渐下降,呈现波动,最后趋于平稳.随着加载速度增加,接触力峰值增大,峰值对应的位移也增大.在初始阶段力-位移曲线的波动是由于动态加载中的惯性效应导致的.在稳定阶段,动态载荷下的力-位移曲线与准静态中的曲线形式基本相同.
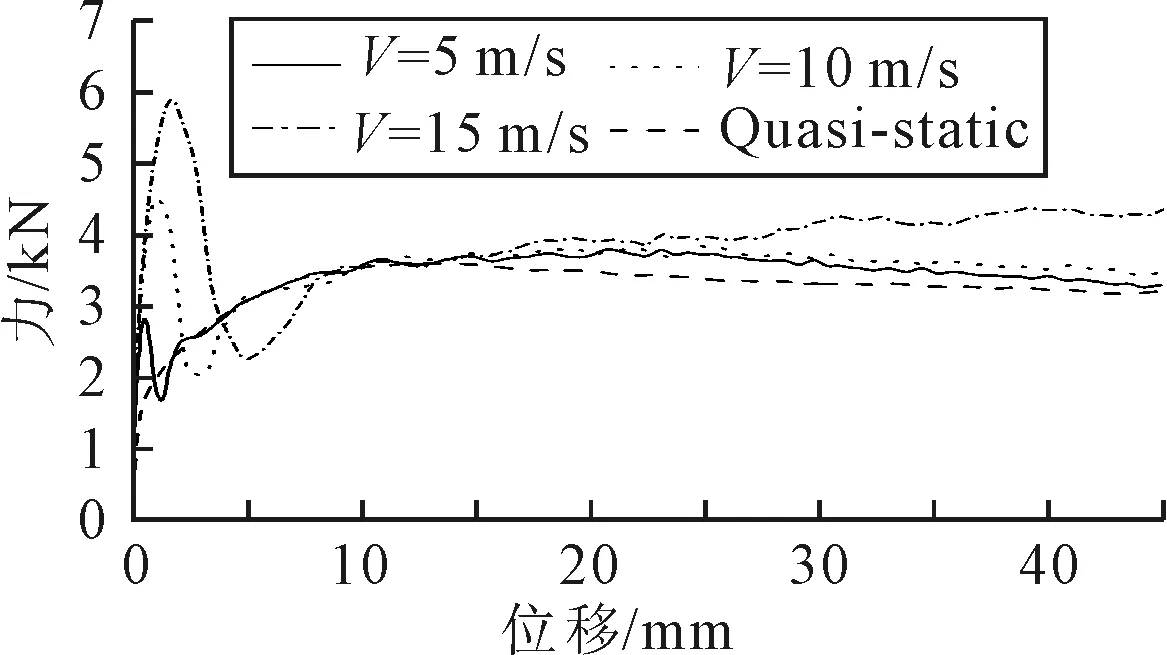
图10 双胞管的动态和准静态载荷下力-位移曲线对比
2.6 能量吸收特性
弯曲过程中不同的能量吸收指标包括吸收的总能量E、比吸能SEA、峰值力Pmax、平均力Pm,以及载荷一致性CFE.总能量E通过积分力-位移曲线得到,SEA是单位质量的能量吸收能力,载荷一致性CFE为平均力和峰值力的比值.计算公式为

(1)
(2)
(3)
表2为2.1~2.4中准静态载荷下,双胞管的能量吸收指标.由表2可见:变形过程中吸收的总能量E随着截面高度、厚度、摩擦因数、压头半径的增加而增大;随着跨距的增加而减小.截面宽度和跨距的增加会降低能量吸收效率SEA,而截面厚度、摩擦因数、压头半径的增大会提高结构的SEA值.载荷一致性CFE随着截面宽度、高度、压头半径的增加而减小,截面厚度、摩擦因数的增加会提高CFE.
表3为2.5中动态载荷下,双胞管的能量吸收特性.随着速度增加,碰撞过程的峰值力Pmax增加,结构吸收的总能量E、能量吸收效率SEA增大,载荷一致性CFE降低.
3 截面变厚度优化设计
以上研究表明,双胞管在三点弯曲载荷作用下,面板、中间和两侧腹板变形特征不同;截面壁厚对能量吸收效率有较大影响.为了得到最优的能量吸收效率,对截面进行变厚度优化设计是一种有效方法.本节用响应面法(response surface method),以获得最大SEA为优化目标,以CFE、壁厚t和质量m作为约束条件,对双胞截面进行优化设计.双胞截面见图11,设计变量:面板厚度t1,外侧腹板壁厚t2,中间腹板厚度t3.双胞管的尺寸为L=250 mm,a=30 mm,b=30 mm.压头和支承半径R=5 mm,跨距s=200 mm,摩擦因素f=0.3,加载速度v=10 m/s.双胞管的质量m=142.8 g,管壁厚度t范围为:0.8~2.4 mm.
响应面法流程见图12,确定设计域变量范围,通过实验设计(design of experiment)选取实验点,数值模拟得到实验点的目标函数值,通过回归分析,拟合得到响应面方程,求解响应面方程得到设计域内目标函数的最优解.对最优解进行检验,如果收敛于规定的公差,则优化结果可信度较高,满足要求.如果偏差较大,则需要调整设计域,采用序列响应面法(sequence response surface method,SRSM)进行再次优化分析,直到最优解收敛.
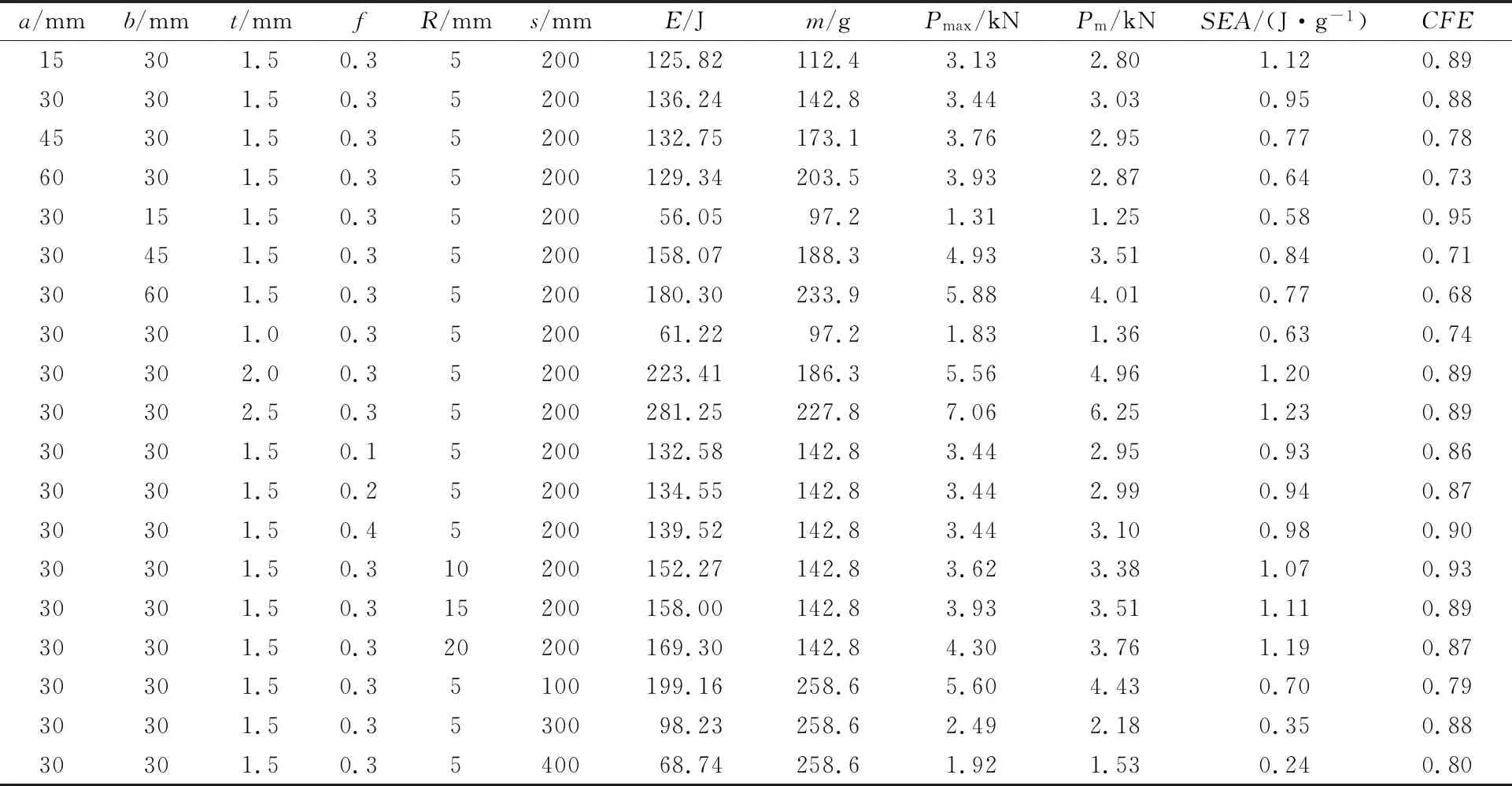
表2 准静态载荷下双胞管的能量吸收特性

表3 动态载荷下双胞管的能量吸收特性

图11 双胞管截面形式

图12 响应面法分析流程
表4为拉丁超立方取样方法在设计域内选取的15个实验点及计算得到的能量吸收指标.在评估能量吸收效率时,SEA和CFE是两个重要的能量吸收指标,选取SEA为目标函数,CFE≥0.75为约束条件,则优化问题简化为
目标:最大化SEA=f(t1,t2,t3).
约束条件:
壁厚约束:0.8 mm≤t1,t2,t3≤2.4 mm.
质量约束:ρ(60t1+60t2+30t3-4t1t2-2t1t3)=148.2 g
载荷一致性约束:CFE=f(t1,t2,t3)≥0.75
选取二次多项式函数,对SEA和CFE用最小二乘法拟合,得到的函数形式为
SEA=f(t1,t2,t3)=-0.330-0.359t1+
0.975t2+0.903t3+0.073t1t2+0.142t1t3-
(4)
CFE=f(t1,t2,t3)=-0.055-0.075t1+
0.427t2+0.516t3+0.078t1t2+ 0.101t1t3-
(5)
求解式(4)~式(5),得到SEA的最大值为1.398 J/g,最优的截面厚度为:t1=0.800 mm、t2=2.400 mm、t3=0.957 mm,对应的CFE为0.789.为检验优化结果的可靠性,对最优截面的双胞管的弯曲过程进行数值模拟.图13为最优截面双胞管的力-位移曲线,数值得到SEA值为1.347 J/g,响应面预测结果比数值结果偏高3.8%,最优解的可靠性较高.最优厚度比均匀厚度的双胞管SEA值高17.9%.
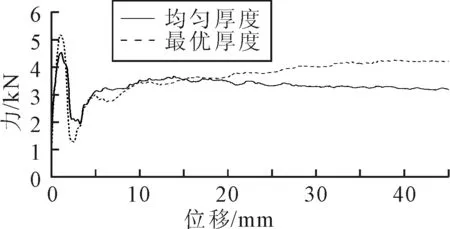
图13 最优厚度和均匀厚度双胞管弯曲过程的力-位移曲线
图14为最优和均匀厚度截面双胞管的变形模式,最优厚度截面发生弯曲变形,而均匀厚度截面出现了凹陷.这说明优化截面厚度,可以改变结构的变形模式,提高能量吸收效率.
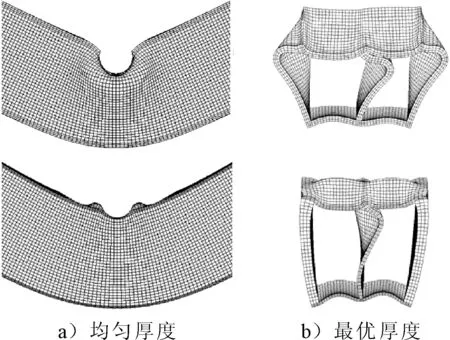
图14 双胞管的变形模式
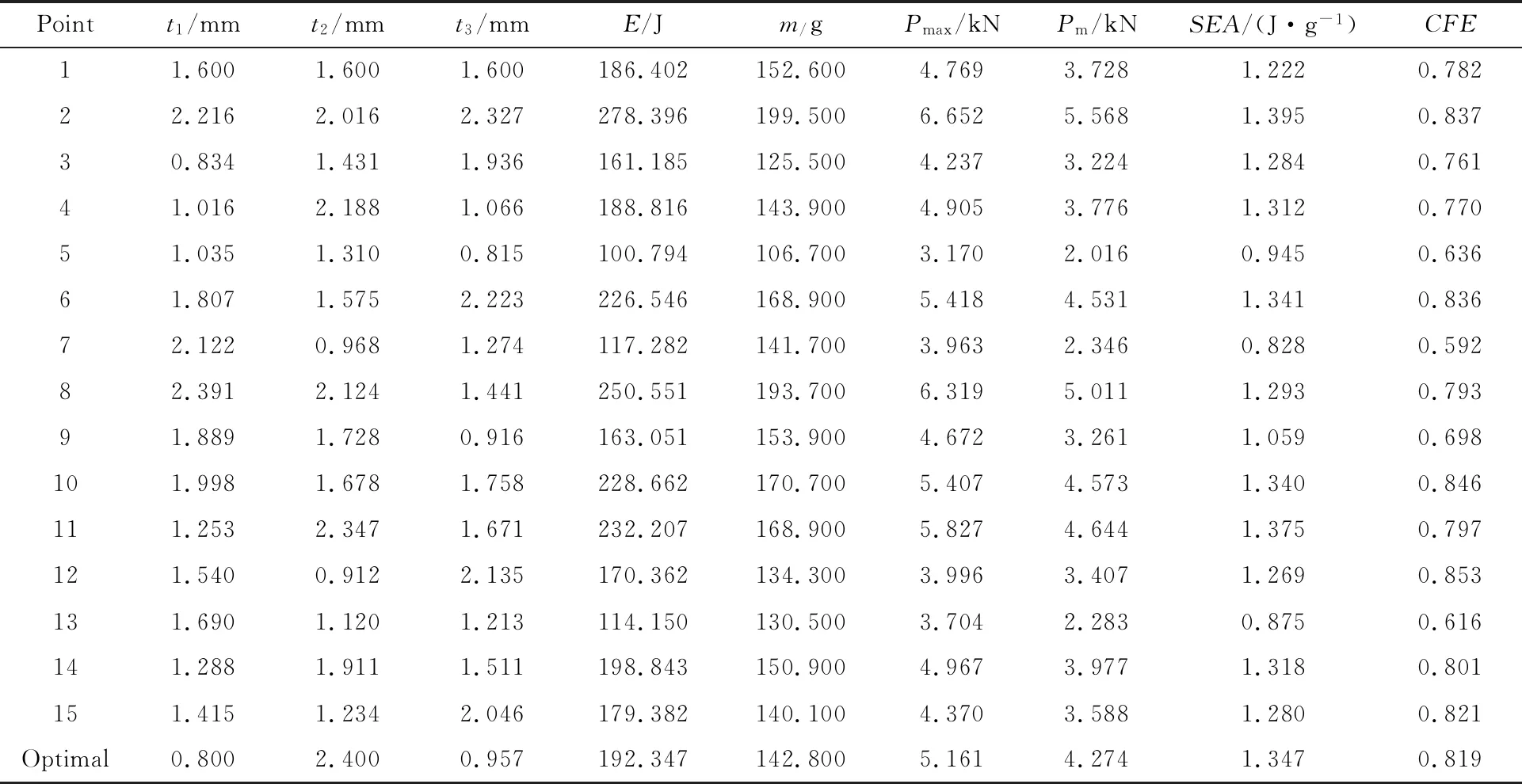
表4 实验点和能量吸收指标
4 结 论
1) LS-DYNA能准确模拟出铝合金管的弯曲变形过程和接触力的响应.
2) 双胞管在三点弯曲载荷作用下的变形特征由弯曲和局部凹陷组成,截面参数和载荷条件对结构的变形模式、接触力响应和能量吸收效率有着重要影响.在载荷作用下,双胞管面板、中间和周边腹板的变形特征不同,吸收的能量不同.
3) 以最大化SAE为优化目标,以质量、壁厚以及CFE值作为限制条件,采用响应面法对双胞铝合金管截面进行变厚度优化设计,响应面法预测结果和数值模拟结果吻合较好.最优截面可以提高双胞管的能量吸收效率,改变结构的变形模式.
