考虑结构损伤的深水桥墩动水效应等效附加质量研究*

2019-08-28邓育林谭金华郭庆康

武汉理工大学学报（交通科学与工程版） 2019年4期

邓育林汤轲谭金华郭庆康

(武汉理工大学交通学院武汉 430063)

0 引言

地震激励下的深水桥墩与周围流场不可避免地产生流固耦合作用，考虑水体的流固耦合模型在计算和分析上比较复杂，许多学者因此做了相应的研究来简化流固耦合模型.Westergaard[1]基于刚性结构和流体不可压缩的假设,研究了地震作用下，水体在垂直坝面上产生的动水压力，并首次提出“附加质量”这一概念；Savage[2]首次对地震作用下墩-水效应进行了研究，计算了柱状桥墩结构周围水体的附加质量；Morison等[3]通过试验研究了水中柱体结构的动水压力分布，并提出了基于绕流理论的半理论半经验公式，即Morison方程.之后，许多学者运用Morison方程或其修正公式对动水压力进行研究，高学奎[4]采用简化的Morison方程，发现动水压力影响随着水深增加而增加; 黄信等[5]分别采用Morison方程及解析方法，对比研究了动水压力作用对桥墩地震响应的影响; 孙竞飞等[6]采用Morison方程、Westergaarrd方程和流固耦合，对比地震作用下动水压力对桥墩的影响.随着结构复杂程度和工程实际对结构模拟要求的提高，解析或半解析法在运用过程中存在一定的局限性；但计算机技术的飞速发展，使得数值法可实现对水体和结构的精确模拟分析，且适用性比较强，也有了一定的研究验证.叶建[7]借助ANSYS软件，单向地震荷载下数值分析法与Morison方程法的计算结果，发现两者的拟合程度很好，基本吻合，但Morison方程法偏保守；方玉成等[8]借助ADINA软件，研究了深水桥梁桩基承台的等效动水附加质量并与基于Morison方程得到的结果对比，得到文中提出的动水附加质量等效模型更符合实际流固耦合数值模型的结论.

然而，以往的研究大多基于Morison方程或者简化的Morison方程，研究的对象也是弹性范围内的结构，但在地震作用下，特别是强震作用下，桥墩很有可能出现损伤，导致局部或者整体结构刚度退化，此时，对于弹性阶段的动水附加质量是否适用于考虑损伤的桥梁结构还没有相关的研究和依据，因此，探究桥墩损伤对动水附加质量的影响具有实际意义.本文基于数值方法，分别考虑深水桥墩结构的一致损伤与局部损伤，同时考虑桥墩墩顶质量的影响，分析了不同墩顶质量及不同损伤程度下的流固耦合系统动水附加质量随水深的变化.

1 有限元模型及分析方法

1.1 墩-水耦合数值模型

以某深水圆柱型桥墩为工程背景，借助有限元分析软件ADINA建立墩-水耦合的三维流固耦合模型，见图1.选取不同墩高的圆形深水桥墩进行分析，墩高分别为40，50，60 m，桥墩截面直径分别为4，5，6 m，壁厚对应为0.7，0.8，0.9 m，不考虑承台与桩基础；在有限元模拟过程中，墩身采用20节点3DSolid单元模拟，水域采用20节点基于势的3DFluid单元进行模拟，桥墩墩底设为固结，在流体与结构的接触面设定流固耦合界面，水域表面设定为自由液面，水域范围取足够大以满足波浪的能量耗散.模型的网格划分综合考虑了计算效率和精度.每5 m取一水位，三种墩高对应最大水位分别是35，45，55 m.模型材料参数设定为：桥墩采用C40混凝土，弹性模量为32.5 GPa，泊松比为0.2，密度为2 500 kg/m3；水域密度为1 000 kg/m3，体积模量为2.2 GPa.

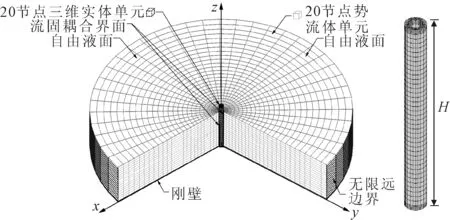
图1 墩-水耦合数值模型示意图

1.2 振型参与质量及动水附加质量计算方法

对于结构振型参与质量的求解，可先将多自由度体系的运动微分方程解耦成n个单自由度振动方程，为

(1)

(2)

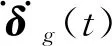
(3)

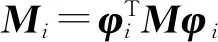
(4)

则各阶振型参与质量以及累计参与质量(各阶振型参与质量之和)为

(5)

对于流固耦合系统中的动水附加质量计算，首先根据广义特征值问题方程.

(6)

以及边界条件

ρFRTU(ω)+MFP(ω)-ρFKFΦ(ω)=0

(7)

得到变换后的特征值方程

(8)

式中：KS，KF分别为结构和流体的刚度矩阵；MS，MF分别为结构和和流体的质量矩阵；R为耦合算子；ρF为流体的密度；U(ω)，P(ω)，Φ(ω)分别为结构的位移矩阵，流体压力矩阵和流体位移势.流固耦合系统的有效参与质量为

(9)

式(9)适用于完全流固耦合系统，当不考虑刚壁边界与流体间的耦合效应时，流固耦合系统的有效参与质量为

(10)

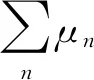
1.3 动水附加质量的计算过程

因为结构所有振型的振型参与质量之和(累计参与质量)等于各质点的质量之和，所以有水与无水情况下的累计参与质量都可以通过数值计算得到.为保证根据式(10)得到的动水附加质量精度足够高，计算桥墩结构以及流固耦合系统累计参与质量的时候应保证计算阶次足够多.为此，通过试算来确定所需计算的振型阶次.图2为三种墩高的桥墩累计参与质量随着计算阶次增加的增幅情况，不同墩高的情况只给出三种水位的变化曲线进行示意.

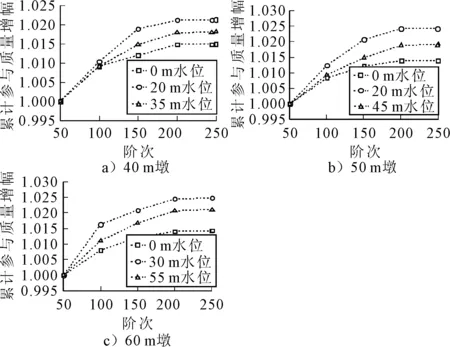
图2 累计参与质量模态阶次试算

由图2可知，试算阶次从200阶开始，水-结构系统在各水位的累计参与质量基本趋于稳定，可以认为此时的累计参与质量即为耦合系统的有效参与质量，在此基础上，可认为有水参与状态下的流固耦合系统累计参与质量与无水状态下结构累计参与质量的差值即为墩-水耦合作用产生的动水附加质量，各工况下的动水附加质量都通过此方法得到.

2 桥墩损伤的影响

有限元分析过程中如果采用考虑墩身损伤的非线性模型，并同时考虑墩身-水的动力耦合效应，则计算非常复杂、耗时巨大，不便于实际运用，为探讨整个地震作用过程中，出现损伤的桥墩动水附加质量的变化情况，可将整个地震时程离散成由许多很短作用时域组成，在每一个作用时域里，可假定结构的损伤程度是不变的，即结构的刚度分布是不变的，针对每一个时刻，可采用前面所述的弹性情况下的方法，计算不同时刻在不同损伤程度下桥墩的动水附加质量，从而得出整个地震作用过程中，桥梁动水附加质量的变化规律.

桥梁上部结构的重量对墩身的动力特性有一定影响，而上部结构对动水附加质量是否有影响还有待探讨，因此本文中考虑不同质量的上部结构即0，1 000，2 000 t，分别等效成桥墩墩顶的附加质量，分布到数值模型墩顶节点中，研究不同墩顶附加质量以及不同桥墩损伤程度对动水附加质量的影响.

2.1 考虑墩顶附加质量的桥墩整体损伤

假定桥墩各截面的损伤程度是一致的(尽管与实际不符，但研究结果仍然有意义)，考虑不同损伤程度，将材料弹性模量折减为原来的10%，30%，50%，70%，90%，计算各水位各墩顶附加质量下不同结构刚度的墩水耦合模型的动水附加质量，并对比不同损伤程度下与无损伤模型的动水附加质量，见图3.

由图3可知，随着水位的升高，不同墩顶附加质量及不同损伤程度工况下的动水附加质量明显增大；同一墩高及同一墩顶附加质量情况下，相同水位不同损伤程度的桥墩动水附加质量之间变化不大；对于某一墩高的桥墩，不同墩顶附加质量情况下，各水位的动水附加质量与无墩顶附加质量时的动水附加质量值几乎相同.墩顶质量影响桥墩动力特性是通过改变桥墩结构的物理特性引起的，而对动水附加质量大小几乎没有影响；桥墩整体损伤也主要是通过改变桥墩刚度而改变结构动力特性，而没有改变动水附加质量，所以可认为桥墩整体损伤及墩顶质量对动水附加质量的大小影响不大，桥墩损伤前的动水附加质量可运用到整体损伤后的动力分析中.

2.2 考虑墩顶附加质量的桥墩局部损伤

假定桥墩出现局部损伤，因为桥墩底部承受较大的结构内力，局部损伤往往出现在墩底部分；将墩底部分材料弹性模量折减为原来的10%，30%，50%，70%，90%，桥墩其余部材料特性分保持不变；各工况下的动水附加质量计算情况见图4.

由图4可知，每幅图中的曲线之间都非常紧凑，且与图3中的曲线规律一致，即桥墩不同程度局部损伤情况下各水位动水附加质量的变化很小，同样的，不同墩顶附加质量对各水位的动水附

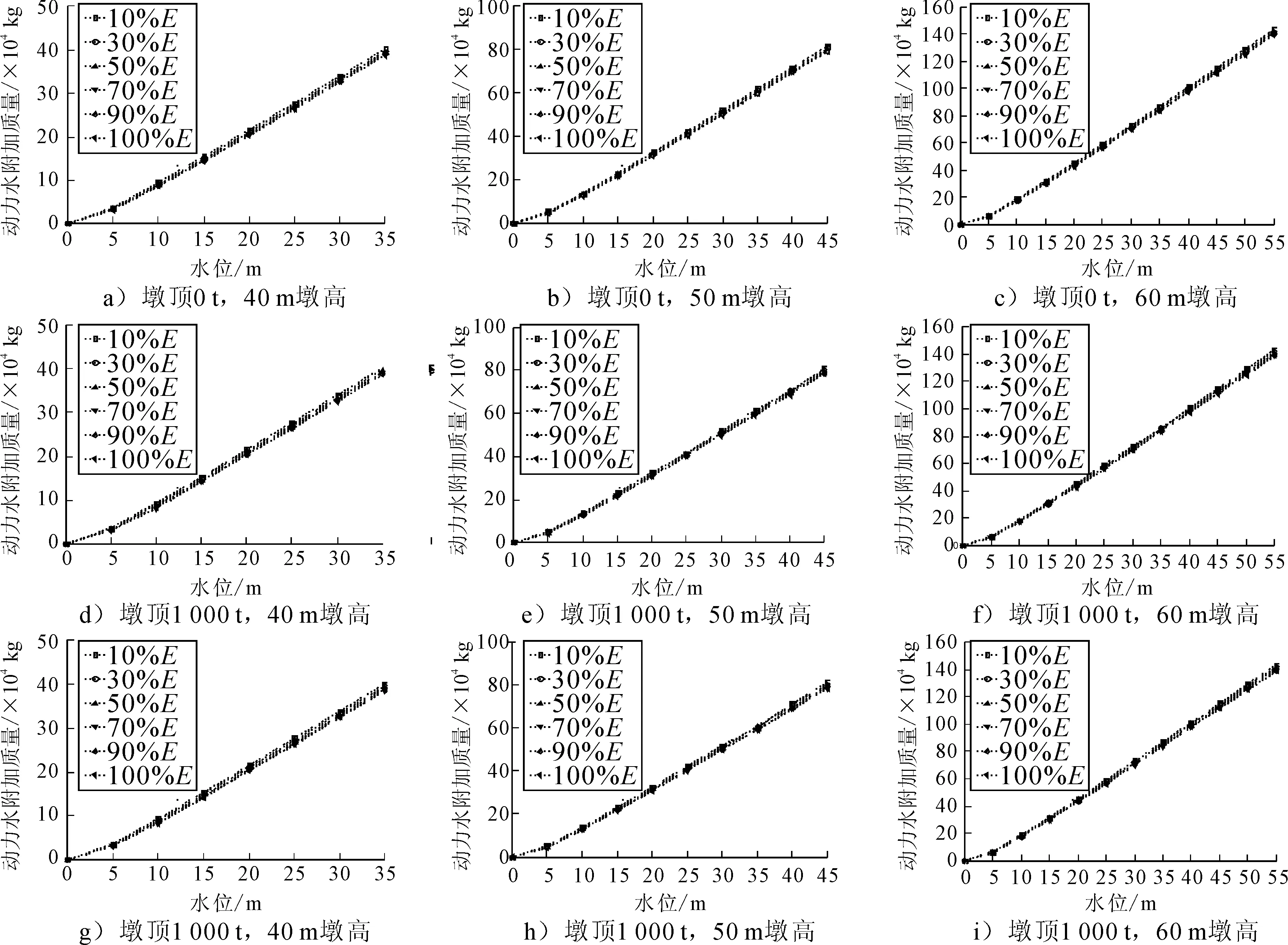
E-结构整体或局部的刚度.图3 不同整体损伤程度下动水附加质量随水位变化曲线

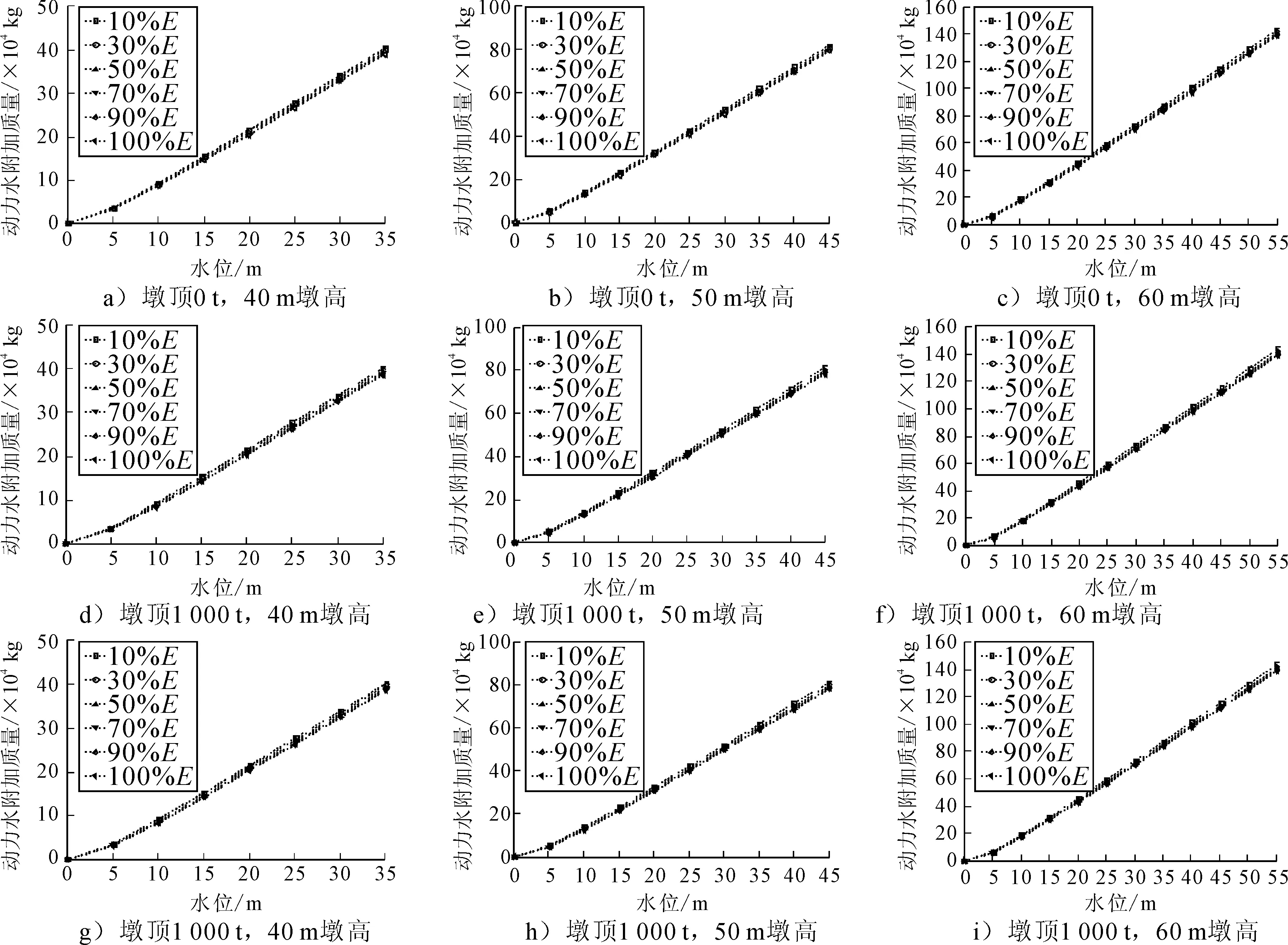
图4 动水附加质量随水位及局部损伤程度变化曲线

加质量的影响几乎没有；所以可认为：墩顶质量以及局部损伤程度对动水附加质量的影响不大，可以采用桥墩损伤前的动水附加质量进行局部损伤后的动力分析.

3 动力特性与动水压力

动水压力与动水附加质量息息相关，为进一步验证以上研究结果，提取流固耦合模型在不同组合工况下沿墩身分布的动水压力，进而对比按动水附加质量等效后模型的自振频率与原流固耦合数值模型的自振频率，综合分析得到最终的结论.最大水位下不同损伤程度的动水压力沿墩身的分布示意图见图5～6；按照无墩顶质量流固耦合模型在弹性阶段计算得到的动水附加质量进行等效，等效前后结构一阶自振周期见图7.图7中只列出40 m墩在考虑2 000 t墩顶质量和不考虑墩顶质量情况下的各水位第一阶模态自振周期和最大水位动水压力分布，其余情况规律一致.

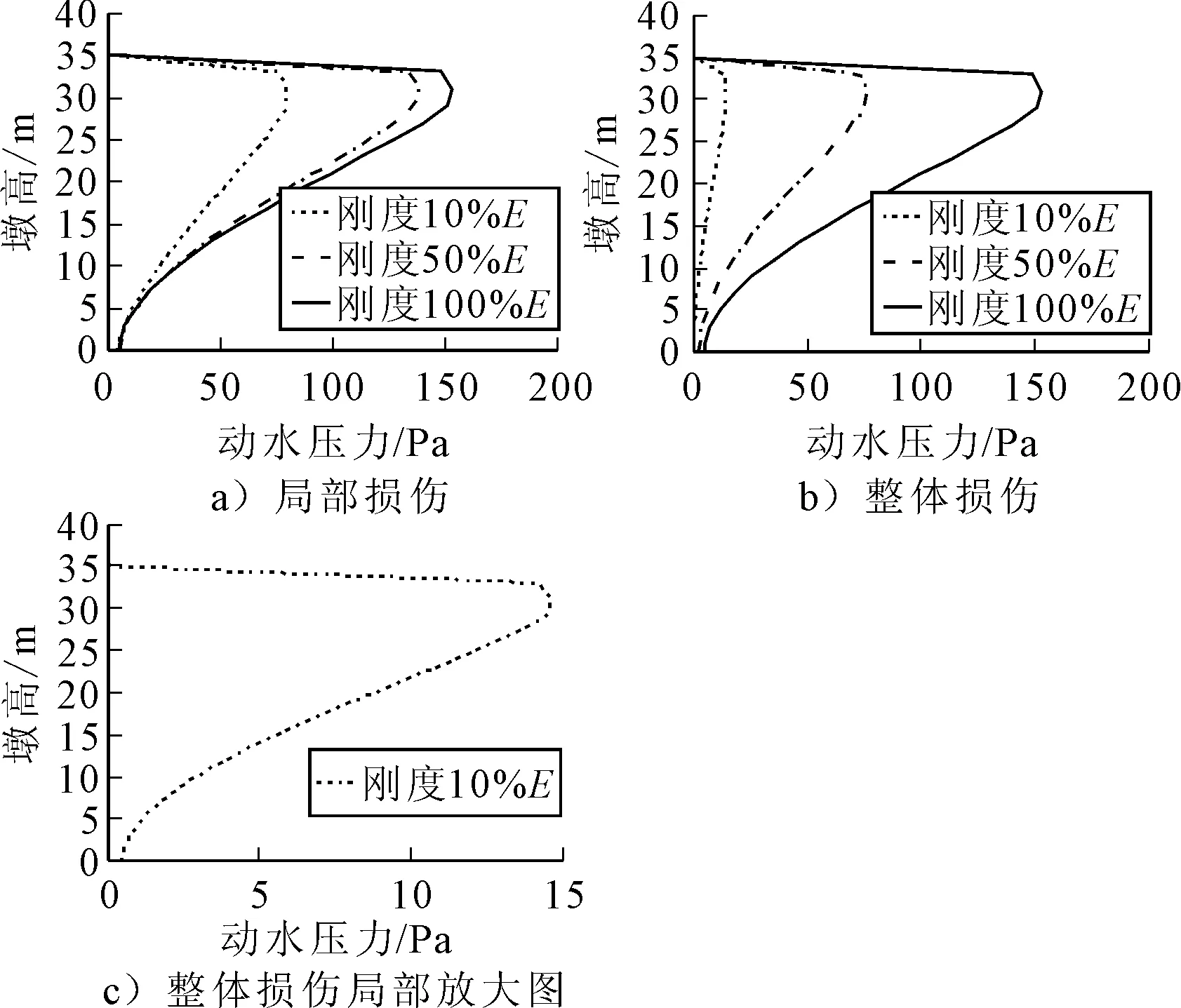
图5 无墩顶质量下动水压力沿墩身分布图

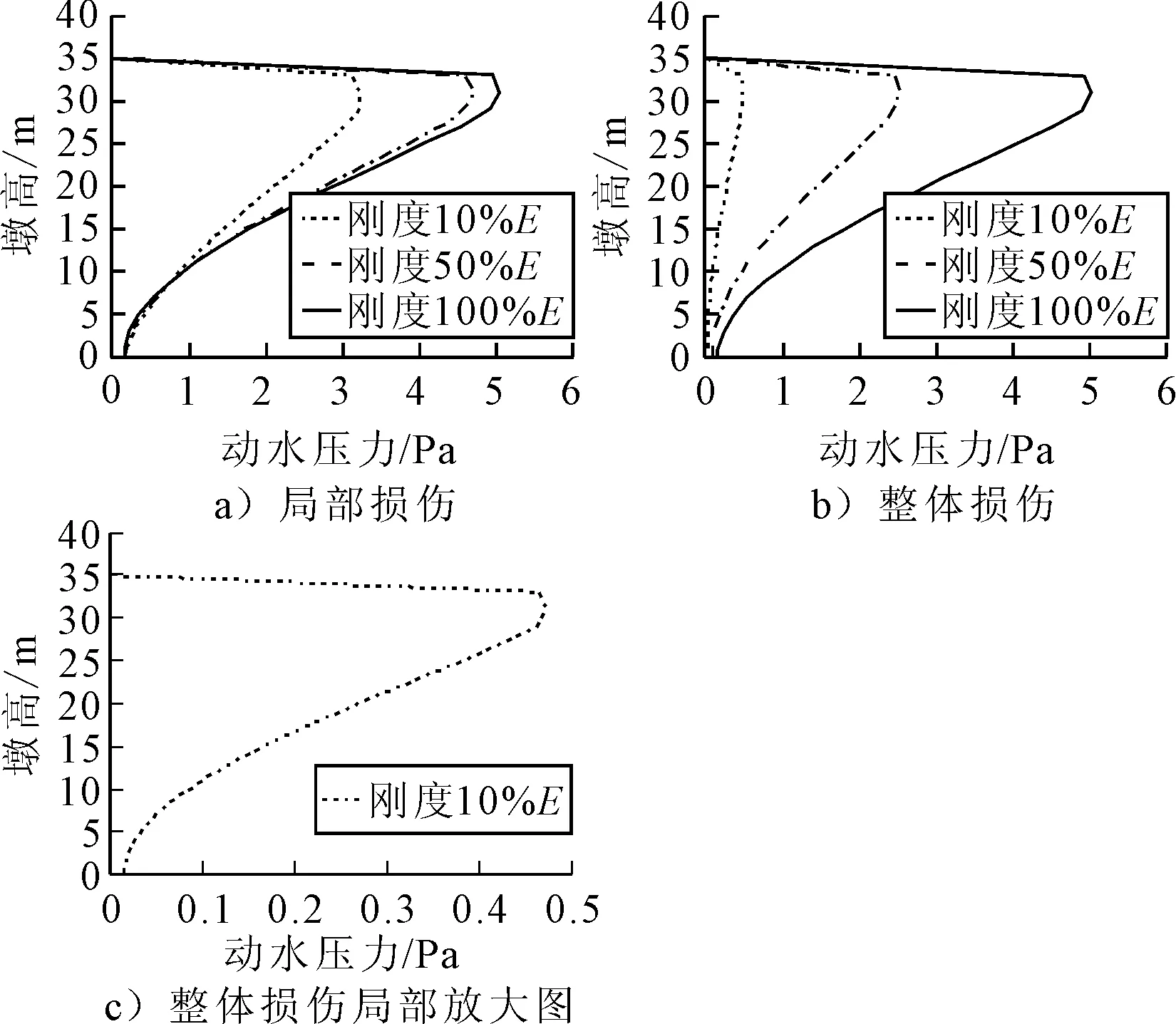
图6 2 000 t墩顶质量下动水压力沿墩身分布图

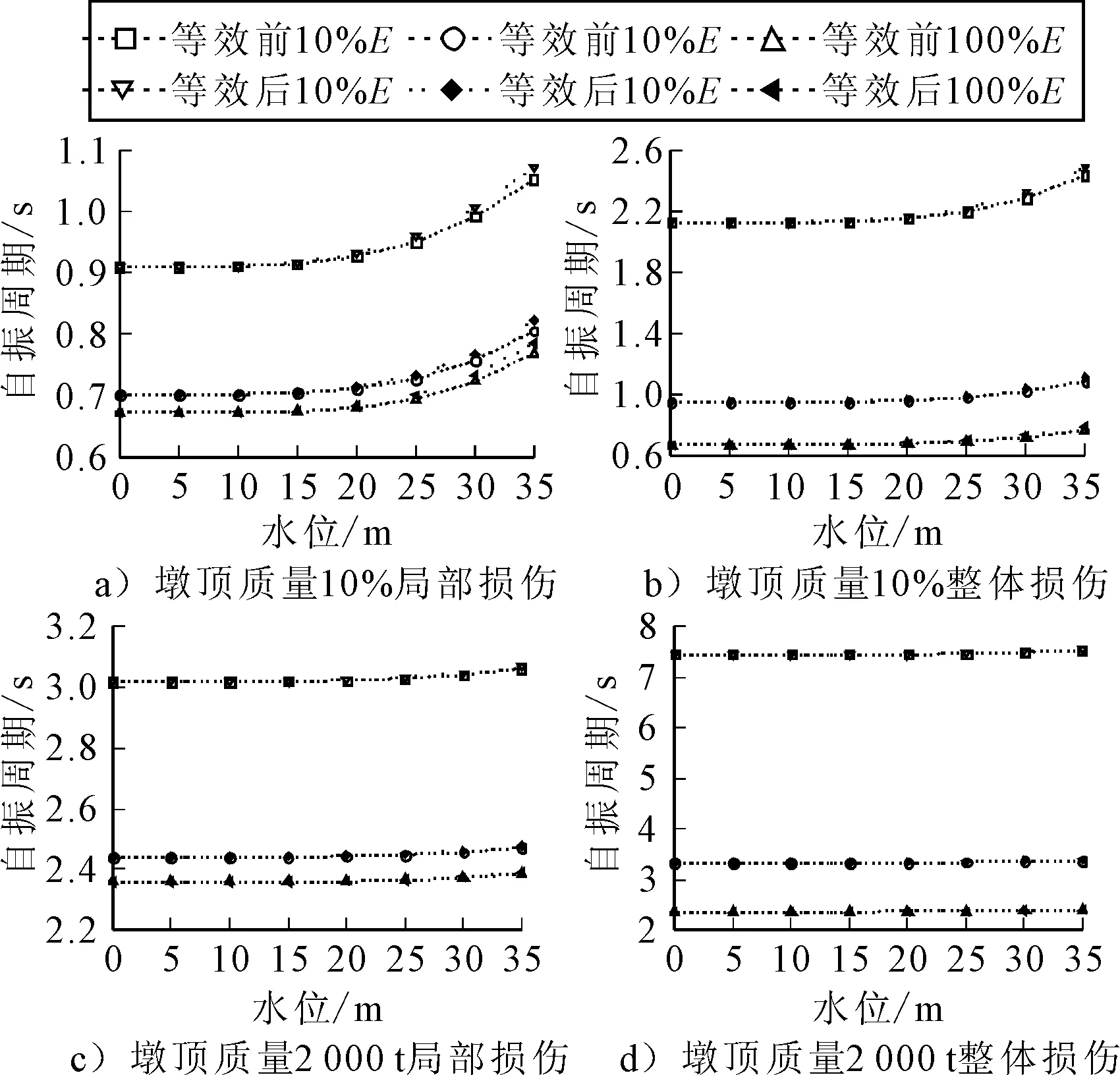
图7 等效前后第一阶自振周期拟合曲线

由图5～图6可知，不管是局部损伤还是整体损伤，刚度折减对动水压力沿墩身的分布规律基本没有影响，而动水压力的峰值随着刚度的减小而减小，对应图7中自振频率随刚度减小而减小的规律；考虑墩顶质量与未考虑墩顶质量情况下，动水压力沿墩身分布规律依然基本相同，但考虑墩顶质量情况下的动水压力峰值要小于不考虑墩顶质量情况下的结果，对应图7中自振周期随着墩顶质量增大而增大；由图7可知，等效前后结构的自振周期随水位的变化拟合较好，验证了第2节中的研究结果.从动水压力分布和动力特性规律可以进一步说明结构损伤与墩顶质量对动水附加质量的大小和沿墩身的分布规律没有影响，弹性阶段下不考虑墩顶质量的动水附加质量可应用于考虑损伤及墩顶附加质量情况下的数值模型中，这样大大提高了深水桥梁在实际地震工程中数值模拟分析的工作效率.