基于电子海图的船舶异常行为识别方法研究*

2019-08-28何正伟刘力荣

武汉理工大学学报（交通科学与工程版） 2019年4期

何帆何正伟杨帆刘力荣

(武汉理工大学航运学院1) 武汉 430063) (内河航运技术湖北省重点实验室 2) 武汉 430063)(国家水运安全工程技术研究中心3) 武汉 430063)

0 引言

随着我国货物载运量和港口吞吐量的快速增长，内河和海域中各类大小船舶数量日益增多，航道的气象、地理、水文和建筑等情况复杂，船舶异常行为逐渐增多，给水上交通安全和人民生命财产带来了严重的威胁.为实现对船舶异常行为的监控，国内外学者做了深入研究.熊勇等[1]采用AIS数据，运用多核函数非参数估计法与假设检验方法辨别在设定航线上出现异常行为的船舶;甄荣等[2]参照平面几何中的点和直线的位置关系，选用多边形区域里的船舶AIS数据，采用多种算法建立了基于贝叶斯分类的船舶异常行为识别模型;邓磊针对内河航道的特征，基于AIS历史数据构建了船舶正常行为模型，运用数据分析和挖掘算法实现了对船舶异常行为的识别；Tang等[3]设计了一种船舶异常行为智能融合系统，在系统中，把一些智能方法融合到一个集成的智能信息处理模块中.

这些方法主要着眼于从宏观上建立整体的监控模型，在实时指导船舶纠正异常行为、避开潜在危险因素、掌握航行状况提供的帮助有限，且在目前来说采用先进平台结合研究的方法较少，因此结合现有平台资源，以智能化的角度分析船舶异常行为成为此方向的研究趋势.文中针对不同角度的四种数学模型方法，基于电子海图平台进行对船舶状态模拟以及重点研究船舶追越问题的实验探讨，寻找有效的船舶异常行为识别方法.

1 船舶行为异常状态的确定

1.1 船舶异常行为概述

船舶异常行为产生的客观和主观原因非常多，对于船舶异常行为识别的定义，Portnoy等[4]认为异常行为可以根据船舶正常行为数学建模与被检测船数据指标之间的差异来定义；Holst等[5]基于模式识别，认为进行异常行为识别需要对大多数船舶行为数据模式进行研究与描绘，进而找出这些少量数据和主要数据在某些典型模式上呈现出来的异同点并进行对比.综合国内外学者的观点，船舶异常行为是指船舶在航行或者锚泊时，出现的非正常行为或者违反水上交通管理规定的行为，船舶异常行为的识别是根据输入的船舶航行相关数据，对船舶的航速、航向、轨迹、船位等要素进行分析，结合船舶所处的地理、环境和气候条件，判断船舶的航行是否符合正常的、普遍的航行运动规律，识别非法运动嫌疑，进而对船舶航行安全及潜在的危险进行评估与预警.

1.2 模型构建方法

基于高曙等[6]对船舶异常行为所提出的关于运动异常和所处空间位置异常两大类及其细分出的16小类，经过分析2016—2017年长江江阴辖区违章船舶的异常行为数据，把船舶异常行为概括为九个方面，见图1.针对这九种船舶异常行为，本文重点提出两类有针对性的船舶异常行为识别方法：时空分析法，航行状态判定法.

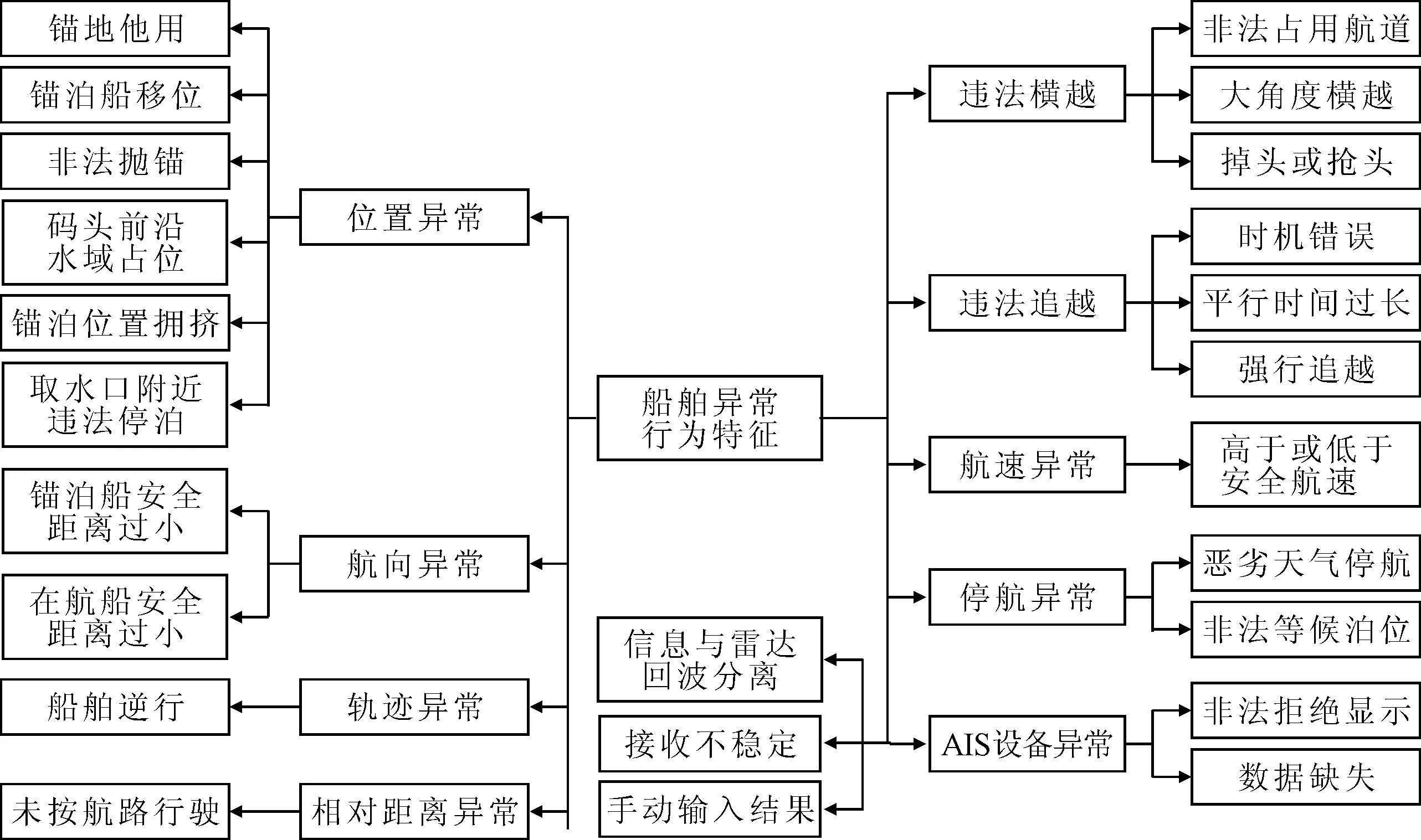
图1 船舶异常行为

2 基于电子海图平台的模型实现

2.1 时空分析法

将船舶AIS数据的时间和船舶所处空间位置及其周边水域情况结合起来，对船舶航行状态进行分析和归纳，找出船舶异常行为并用数学模型对其进行表征.重点对提出关于的后八种异常类别可细分为：位置判定、相对距离判定、轨迹判定、航向判定.

2.1.1位置判定

针对位置异常中的后三类现有研究方法较少的异常建立位置判定数学模型.

1) 针对码头前沿水域是否发生占位的判定，由于码头前沿水域的宽度不固定，其宽度和标准船长有直接关系，因此本文采用距码头前沿两倍标准船宽范围内的区域作为码头前沿水域[7].图2为计算模型获取码头前沿水域范围.

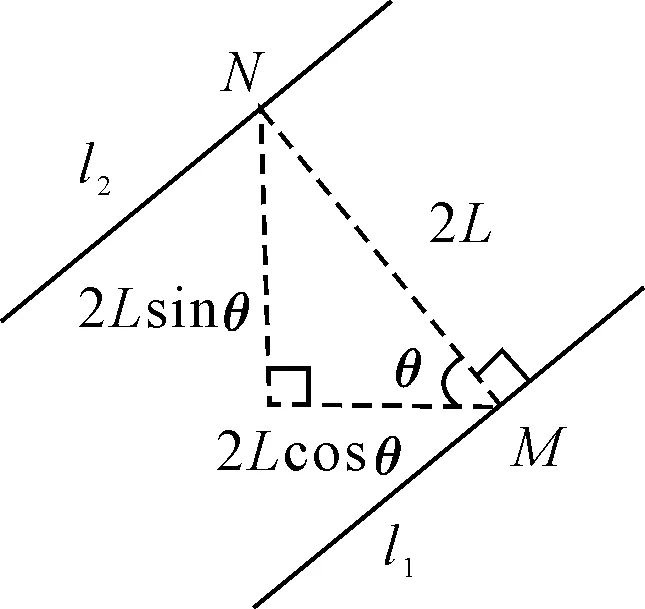
图2 码头前沿水域范围的计算模型

设码头前沿的某段线段为l1，其表达式为Ax+By+C=0，由于l1上任意两点的经纬度坐标是可知的，所以l1的表达式也是可知的.设l2为码头前沿水域的边界，L为标准船宽，则l2与l1的距离|MN|为2L.设MN与纬线的夹角为θ，由于(90°-θ)为码头前沿l1与纬线的夹角值，该值可从航道数据获知，所以θ是可知的.因而，根据直线平移的公式，码头前沿水域的边界l2的表达式可表示为：A(x-2Lcosθ)+B(y-2Lsinθ)+C=0.

如何影响他船靠离泊的船舶在码头前沿水域范围内，则满足Ax+By+C<0和A(x-2Lcosθ)+B(y-2Lsinθ)+C>0这两个条件.

在藤井船舶领域模型[8]中，内河船舶的领域模型是一个椭圆，该椭圆有如下性质：长轴的长度为6L0，短轴的长度为1.6L0，L0为船长.

假设影响他船靠离泊的船舶在码头前沿水域范围内，其位置为D(m,n)，以该点为圆心作一个椭圆，其长轴为6L1，短轴为1.6L1，L1为该船船长，为便于研究，令长轴与经线平行，短轴与纬线平行.设要靠离泊的船舶位置为K(x,y)，其值不断变化.在某一时间段内，若K点进入在椭圆内，则船舶靠离泊的过程是不安全的，有碰撞的危险，其函数关系为

(1)

式中：D(m,n)为影响他船靠离泊的船舶；K(x,y)为要靠离泊的船舶位置；L1为影响他船靠离泊的船舶的船长；L为标准船宽；θ为MN与纬线的夹角；f(x,y,m,n)为判定结果.当U、V和W这三个集合的逻辑运算结果都为真时，f(x,y,m,n)才为真，此时，码头前沿水域内存在影响他船靠离泊安全的船舶.

2) 针对锚泊位置拥挤的判定，即判定有采砂、锚泊等行为的船舶是否处于航道中，可以借鉴第1)类关系的判定方法.假设有采砂、锚泊等行为的船舶的位置为D(m,n)，如果该船位于航道中，则该船不在码头前沿水域范围内，此时，其满足的数学关系为A(m-2Lcosθ)+B(n-2Lsinθ)+C<0.

假设有采砂、锚泊等行为的船舶在航道中，以其位置点D(m,n)为圆心作一个椭圆，长轴为6L1，短轴为1.6L1，L1为该船船长，为便于研究，令长轴与经线平行，短轴与纬线平行.设在航道中航行的某船舶的位置为K(x,y)，其值不断变化.在某一时间段内，若K点因航道宽度、吃水深度、航道中的障碍物、其他船舶影响或者人为操作等原因，不得不进入有采砂、锚泊等行为的船舶的领域椭圆内运动，则在航道中航行的船舶是不安全的，其函数关系为

(2)

式中：D(m,n)为有采砂、锚泊等行为的船舶的位置；L1为该船船长；v为该船航速；K(x,y)为在航道中航行的某船舶的位置；L为标准船宽，θ为MN与纬线的夹角，f(x,y,m,n,v)为判定结果.当V,W和X这三个集合的逻辑运算结果都为真时，f(x,y,m,n,v)才为真，此时，航道内存在采砂、锚泊等有碍通航安全的船舶.

3) 针对船舶是否非法停泊，根据船速在某段时间内的变化情况，如果船速一直不超过0.2 kn，则船舶处于停泊状态[9].结合取水口位置及杨梅等人对取水口等级的划分规则[10-11]判断停泊状态并设计取水口保护区的计算模型，见图3.内部矩形为一级保护区，外部矩形为二级保护区.令取水口的位置坐标为点F(m,n)，水流方向与纬线的夹角为θ.以一级保护区为例，U1为取水口上游的长度(U1可取1 500 m)，D1为取水口下游的长度(D1可取100 m)，C1为沿岸陆域纵深(C1可取50 m)，则可通过集合运算得出一级保护区四个顶点坐标，如点L的坐标为

(3)

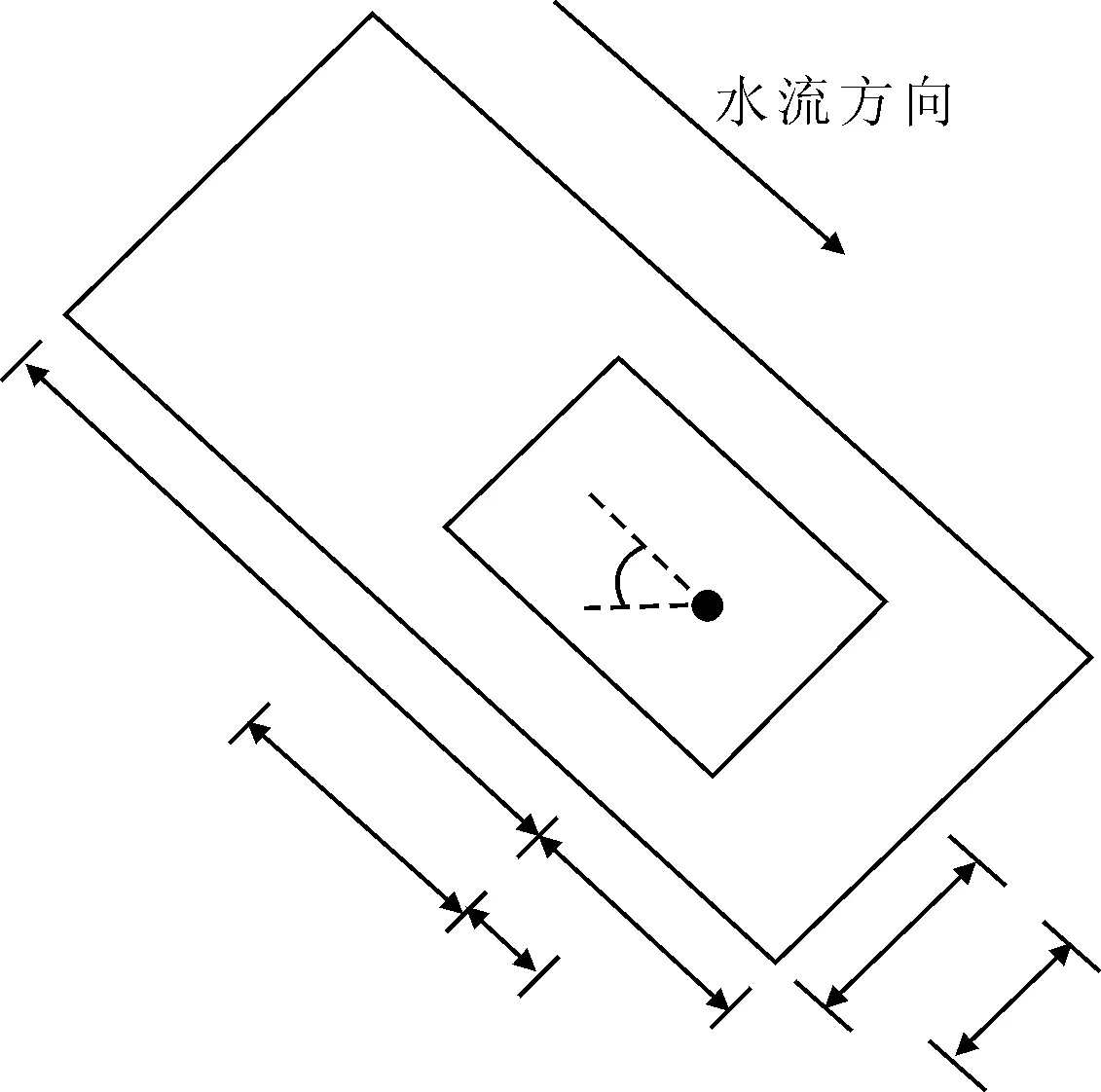
图3 取水口保护区的计算模型

由此可得出举行四条边的函数表达式为：KL:P1X+Q1y+R1=0，LM:P2x+Q2y+R2=0，MN:P3x+Q3y+R3=0，NK:P4x+Q4y+R4=0.如果取水口一级保护区内有船舶违规停泊，其函数关系可用式(4)来表示.

(4)

式中：{x,y}为违规停泊的船舶的坐标；v为该船的航速；P、Q和R均为待定系数；f(x,y,v)为判定结果.当H，I，J，K和X这五个集合的逻辑运算结果都为真时，f(x,y,m,n,v)才为真，此时，取水口保护区内有船舶违规停泊.

如果采用以二级保护区作为判定基准，则U2为取水口上游的长度(U2可取3 500 m)，D2为取水口下游的长度(D2可取300 m)，C2为沿岸陆域纵深(C2可取1 000 m)，其余计算过程均与一级保护区相似.

2.1.2相对距离判定

1) 针对锚泊船安全距离由于海事部门的动态监管规范没有对两船间的安全距离作出硬性规定，本文根据藤井船舶领域模型来进行分析，在内河中，两船间的安全距离不能小于船舶领域椭圆的短半轴0.8L0，L0为船长.由于两船的长度往往不一样，两船的船舶领域大小也往往不一样，为安全起见，应采用长度较大的船舶的领域模型，所以在0.8L0中，L0为长度较大的船舶的船长.

对于锚泊船，要先判断船舶是否处于锚泊状态.查看AIS数据，在某一时间段内，如果两船的航速都不超过0.2 kn，则两船都处于停泊状态.设两锚泊船间的安全距离为s，令s=0.8L0，两锚泊船的位置分别为K1(x1,y1)和K2(x2,y2)，如果两船距离大于或等于安全距离，则两船都是安全的，其函数关系表达为

(5)

式中：K1(x1,y1)和K2(x2,y2)分别为两锚泊船的位置；s为两锚泊船间的安全距离；v1和v2分别为两锚泊船的航速；f(x1,x2,y1,y2,v1,v2)为判定结果.当L、X和Y这三个集合的逻辑运算结果都为真时，f(x1,x2,y1,y2,v1,v2)才为真，此时，两锚泊船间留有足够的安全距离.

2) 针对在航船舶安全距离设两在航船舶间的安全距离为s，令s=0.8L0，两在航船舶的位置分别为K1(x1,y1)和K2(x2,y2)，它们的位置会随时间的变化而变化.如果两船距离大于或等于安全距离，则两船都是安全的，其函数关系表达为

(6)

式中：K1(x1,y1)和K2(x2,y2)分别为两在航船舶的位置；s为两在航船舶间的安全距离；v1和v2分别为两在航船舶的船速；f(x1,x2,y1,y2,v1,v2)为判定结果.当L、X和Y这三个集合的逻辑运算结果都为真时，f(x1,x2,y1,y2,v1,v2)才为真，此时，两在航船舶间留有足够的安全距离.

2.1.3轨迹判定

选取某一小段河流作为研究对象，假设其走向为自西向东，图4为船舶轨迹与定线制规定的航路.其中点A(a,b)和C(e,f)为该段船舶轨迹中纬度最低的两个点，B(c,d)为该段船舶轨迹中纬度最高点，若其全都位于多边形区域内，则该段船舶轨迹全都位于定线制规定的航路内.

图4 船舶轨迹与定线制规定的航路

以点A为例，假设过点A的水平直线与多边形区域有mA个交点，与多边形边界左侧交点有mA1个，右侧的交点有mA2个；依次类推定义点B和点C与多边形边界交点.则根据奇偶规则法(even odd rule)，若mA1，mA2，mB1，mB2，mC1和mC2均为奇数，则该段船舶轨迹全都位于定线制规定的航路内，其函数关系表达为

f(mA1,mA2,mB1,mB2,mC1,mC2)=

{mA1|mA1∈S}∧{mA2|mA2∈S}∧

{mB1|mB1∈S}∧{mB2|mB2∈S}∧

{mC1|mC1∈S}∧{mC2|mC2∈S}

(7)

式中：S={1,3,5,7,…}；f(mA1,mA2,mB1,mB2,mC1,mC2)为判定结果；mA为过点A的直线与多边形区域的交点总数；mA1为点A左侧的交点数；mA2为点A右侧的交点数；mB，mB1，mB2，mC，mC1和mC2的意义依此类推.当式中的六个集合的逻辑运算结果都为真时，f(mA1,mA2,mB1,mB2,mC1,mC2)才为真，此时，该段船舶轨迹全都位于定线制规定的航路内.

2.1.4航向判定

船舶航行时，尽管船首向会在一定范围内微小变动，但航向是基本稳定的，而逆向行驶相对于航向偏移会造成更加严重的水上事故，因此本文以此为例，采用矢量分析法对船舶反向行驶情况进行判定.设某一时刻该船舶位置为K1(x1,y1)，下一时刻该船舶位置为K2(x2,y2)，则其行驶方向矢量为D(x2-x1,y2-y1)；从航道中的其他船舶中选取一些船舶采用上述方法，计算出它们行驶的平均方向矢量Ek(xn+1-xn,yn+1-yn)，n为某一时刻，n+1为下一时刻.

如果D(x2-x1,y2-y1)和Ek(xn+1-xn,yn+1-yn)的夹角θ大于90°且小于或等于180°，则该在航船舶处于反航道行驶状态.g(D·Ek)代表D·Ek的全部值的集合，其应满足的条件g(D·Ek)可用下式表示，此时，海事部门应及时对其发出警告和指导.

2.2 基于航行状态判定法的船舶异常行为识别方法

船舶的航行状态与航速息息相关，在航行状态判定法中，船舶航速是否符合定线制规定的安全航速，决定着船舶是否违章.不同的内河航道，定线制规定的航速是不一样的；同一内河航道的不同地段，定线制规定的航速也不尽相同.本文将此方法细分为两种方法：航速判定法、停航判定法.

2.2.1航速判定

1) 针对在航情况观察AIS数据，在某一时间段内，如果船舶的航速均大于0.2 kn，则船舶处于在航状态.参照定线制规定的安全航速，设航道内定线制规定的安全航速为：最低航速v1，最高航速v2，如果船舶航速小于或等于最高航速，则该船舶没有超速，其应满足的条件集合g(v)表示为

g(v)={v|0.2 kn≤v≤v2}

(9)

2) 针对锚泊情况参照定线制规定的安全航速，设航道内定线制规定的安全航速为：最低航速v1，最高航速v2，在足够长的时间段内，如果船舶航速小于最低航速，则该船舶的航速确实长时间低于定线制最低限速，其应满足的条件集合g(v)表示为

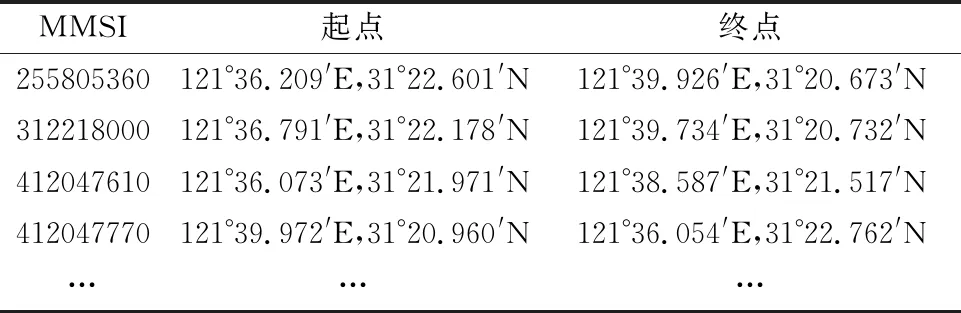
g(v)={v|0

(10)

2.2.2停航判定

1) 针对恶劣天气停航情况由AIS数据，如果船舶航速持续大于0.2 kn或时开时停，则船舶违章冒险航行.v为船舶航速，其应满足的全部值集合为g(v)：

g(v)={v|v>0.2 kn}∪

{v|有时v>0.2 kn有时v≤0.2 kn}

(11)

2) 针对码头泊位行为的判定运用前文的位置判定法可若船舶航速持续小于或等于0.2 kn，则船舶确实长时间停滞在江中等码头泊位，其应满足的条件g(v)为

g(v)={v|v≤0.2 kn}

(12)

3 实验结果与分析

3.1 基于电子海图平台的船舶行为绘制

采用2017年12月29日12:00—13:00时段的完整AIS模拟数据对地理位置较为复杂且船舶异常频发的长江上海段出海口处的南港水道中经纬度在121.60°E～121.67°E，31.33°～31.42°范围进行船舶行为研究.以每条船舶的MMSI唯一作为区别条件，以等腰三角形代表船身、顶点代表船首向，间隔时段获取到的AIS数据进行显示并进行轨迹连线，形成时段内完整的船舶轨迹.图5为绘制出的本段时间范围内所有船舶的连续轨迹.

图5 南港水道内艘船的轨迹

由图5可知，经过二次开发后的电子海图平台可根据自选AIS数据将一定范围内特定船舶在此时段内的运动方向和位置直观地体现出来.表1为部分船舶的MMSI、起点和终点.

表1 南港水道内部分船舶的MMSI、起点和终点

3.2 违法追越行为识别

以船舶违法追越为例，采用2016年12月6日06:21—06:57的长江江阴段的明文AIS违法追越在线数据进行实验.在大量行为中，选取06:21:03—06:57:36时段MMSI为412765470的船舶(追越船)在本时段违法追越MMSI为412590420的船舶(被追越船)为例并选取5个时刻观察期运动状态，其详细数据见表2，其追越状态2～4在电子海图上表示见图6.

表2 船舶追越状态位置及时刻显示

图6 船舶追越状态

由距离计算功能及绘制显示可知，追越状态3时追越船与被追越船相距132.152 m.此时追越船已经追上被追越船，两船并排行驶；追越状态4时，追越船与被追越船相距382.577 m，追越船已经超过被追越船，位于被追越船的左前方.追越船的航向开始向右偏转，意欲返回追越发生前的航路，该航路与被追越船的航路一致.

根据应用于电子海图平台的上述数学模型对于状态2的预测可知，此时两船处于违法追越与被追越状态.而根据海事部门动态监管规范，在内河中，并排行驶的两艘船的安全距离不能小于船舶领域椭圆的短半轴0.8L0，L0为两船中较长的船舶的船长，则L0为190 m，0.8L0等于152 m.追越状态2时，两船距离132.152 m小于安全距离152 m，被追越船位于追越船的领域模型之内，两船易出现紧迫局面，甚至有碰撞的风险，因此,可被判定为违法追越行为，与模型预测一致.

通过使用AIS实验数据的模型测算与实际两船安全距离标准，与平台显示出的违法追越进行对比，重复实验50次，正确描绘船舶违法追越轨迹且船舶位置经纬度显示正确的次数为41次，准确率为82%.其误差可能来源于AIS设备传输信息不完备或数据缺失.