惯导辅助的动对动整周模糊度快速解算方法

朱楚江,赵修斌,庞春雷,张 良,伍劭实,赵钟炎

(空军工程大学信息与导航学院,陕西 西安 710077)

0 引言

动对动高精度相对定位技术在飞行器空中交会对接、飞机空中加油以及舰载机着舰等军事应用中具有重要作用[1]。与传统北斗高精度动态相对定位相比,动对动相对定位具有以下特点:首先,基准站的位置实时变化,其准确位置无法得知；其次,动对动相对定位对于精确地在航实时解算整周模糊度要求较高。在卫星信号发生遮挡或者信号质量不佳时,接收机的载波相位观测值将会产生周跳,此时需要对模糊度进行重新初始化,但这需要十几分钟甚至更长时间[2],因此难以实现整周模糊度的快速解算。文献[3]提出利用解耦法以及奇异值分解法来消除基线参量,并实时推算双差整周模糊度的浮点解及其协方差矩阵,旨在实现模糊度的动态初始化,其整周模糊度固定时间为69 s。文献[4]采用奇异值分解法消除了基线向量,并运用递推最小二乘法实时推算模糊度浮点解及其协方差矩阵,有效缩短了模糊度的初始化时间,但还无法有效实现动对动条件下由于卫星信号遮挡导致的模糊度快速解算问题。

惯导具有短时精度高、自主性强的特点,能够在北斗信号发生遮挡或者信号质量较低时维持短时的高精度状态输出[5],从而实现模糊度的快速解算。本文针对此问题,提出了惯导辅助的动对动整周模糊度快速解算方法。

1 INS辅助北斗相对定位

为了获得较高精度的定位结果,北斗相对定位通常采用载波相位差分的方法来进行定位,其精度可达毫米级[6]。为了消除卫星钟差、接收机钟差及大气传播延时误差,通常采用载波相位双差模型[7]。忽略双差测量噪声,考虑到用户接收机到卫星的几何距离和基线向量之间的几何关系,可将其观测方程写成矩阵形式为:

(1)

传统动态相对定位方法无法满足模糊度的动态实时固定,因此需要寻找整周模糊度在航实时解算的新方法,实现动态条件下的模糊度初始化[8]。

由于惯导在短时间内能够保持较高精度的状态输出,所以本文考虑利用惯导来辅助整周模糊度的动态解算[9]。具体做法为:在双差载波相位观测值的基础上,引入INS的实时三维位置输出,并将其与双差载波相位观测值进行组合,形成新的观测量,构建新的观测方程,然后对双差整周模糊度进行固定求解[10]。其算法流程图如图1所示。

当基准站的位置固定不变时,其精确位置坐标已知,此时只需在移动站上加一个惯导对其实时位置进行估计,大多数惯导辅助相对定位研究也是基于固定基准站的情形来展开的[11-12]。当基准站位置也实时变化,如两个运载体进行实时动态相对定位时,没有基准站的精确位置坐标可作参考。本文将基于固定基准站的惯导辅助北斗动态相对定位算法推广到动态基准站的情形,提出了动对动条件下惯导辅助北斗整周模糊度解算新算法。

图1 INS辅助北斗整周模糊度解算算法Fig.1 BDS integer ambiguity resolution with INS aiding

2 动对动条件下INS辅助北斗整周模糊度解算新算法

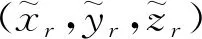
图2 INS辅助BDS相对定位示意图Fig.2 Schematic diagram of BDS relative positioning with INS aiding

卫星i到运载体r的实际距离为:

(2)

测量距离为:

(3)

(4)

式(4)中,泰勒展开式系数

惯导位置估计偏差

同理可得:

(5)

(6)

(7)

为了消除钟差及大气误差影响,对两个运载体的载波相位测量值作双差,得到的载波相位双差方程为:

(8)

式(8)中,

(9)

将式(8)进一步表示为:

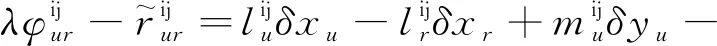
(10)

Z=HX

(11)

根据最小二乘原理,式(11)的最小二乘解为:

X=(HTH)-1HTZ

(12)

协方差矩阵为:

QX=(HTH)-1

(13)

由式(12)和式(13)可分别得到双差整周模糊度的浮点解和协方差矩阵,然后通过LAMBDA算法固定模糊度,最后将固定了的双差模糊度代入式(1)反解基线向量bur,从而实现相对定位。

3 仿真实验验证

3.1 实验数据仿真

在本仿真实验中,首先利用卫星导航信号模拟器模拟多颗卫星在一段时间内的运行轨迹,并得出卫星在这段时间内的位置坐标。然后利用轨迹发生器产生出两段轨迹,分别作为用户以及移动基准站的运动轨迹,并根据这两段仿真轨迹对惯导数据进行仿真,得到仿真惯导在每一时刻的实时位置输出。最后根据卫星位置坐标以及仿真轨迹,对载波相位观测值以及单位视线向量进行仿真。其中,在对载波相位观测值进行仿真时,加入0.01周的载波相位观测噪声；根据卫星位置以及惯导跟踪轨迹,对新引入的惯导距离差分量以及泰勒展开式系数进行计算。

由于实验数据均通过仿真得到,所以整周模糊度的准确值可事先求得。本实验参与解算的卫星数为9颗,由此产生的8个双差整周模糊度的准确值如表1所示。

表1 双差整周模糊度准确值

本实验在对用户接收机以及移动基准站的轨迹进行仿真时,保持基线长度始终为2 m,用户接收机以及移动基准站均以2 m/s的速度向同一方向匀速移动。其中用户接收机仿真轨迹及惯导跟踪轨迹如图3所示(移动基准站的仿真轨迹及惯导跟踪轨迹与此类似)。

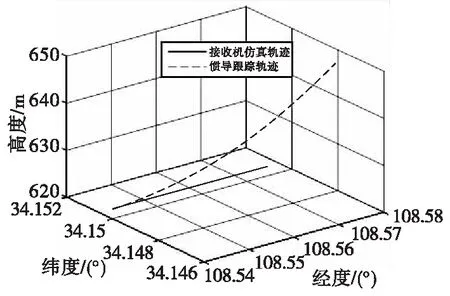
图3 接收机仿真轨迹Fig.3 Receiver simulation track

3.2 仿真解算结果

先用最小二乘法得出整周模糊度的浮点解及协方差矩阵,再利用LAMBDA算法将整周模糊度进行固定,固定过程如图4所示,固定结果及固定时间如表2所示。然后将固定了的整周模糊度代入载波相位双差观测方程求解基线向量。解得的基线长度结果如图5所示,相对定位精度如图6所示。此外,去掉惯性辅助再做一次仿真实验进行对照,以第一个模糊度为例其整周模糊度固定过程如图7所示。

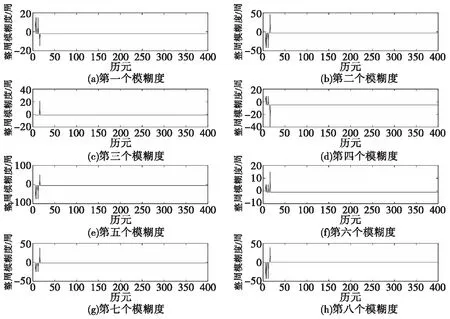
图4 整周模糊度固定情况Fig.4 Integer ambiguity fixing

N21N31N41N51N61N71N81N91固定时间/s固定值-2-3-1-5-5-1-2016

图5 基线长度Fig.5 Baseline length

从实验结果可以看出,加入惯性辅助后整周模糊度的固定值与准确值完全一致,反解得到的基线长度误差在2 cm以内,X,Y,Z三个方向的定位精度均在2 cm以内,整周模糊度的固定时间仅为16 s,而没有惯性辅助时整周模糊度的固定时间为49 s。这表明,加入了惯性信息辅助的双差观测方程与仅有载波相位信息的传统双差观测方程相比,短时间内观测方程的强相关性有了较大程度的削弱,法矩阵的严重病态性也有了很大程度的改善。

图6 相对定位精度Fig.6 Relative-position accuracy

图7 无惯性辅助模糊度固定情况Fig.7 Integer ambiguity fixing without INS aiding

3.3 浮点解误差分析

为了分析惯导辅助对整周模糊度浮点解误差的影响,以第一个模糊度为例,将惯导位置误差设置为1 m进行仿真，仿真结果如图8所示。从仿真结果可以看出,惯导的辅助使得整周模糊度浮点解更加靠近其真值。说明加入惯性信息可以减小模糊度浮点解的误差,压缩模糊度的搜索空间,提高搜索效率。

图8 惯导辅助对整周模糊度浮点解误差的影响Fig.8 INS aiding influence integer ambiguity floating solution error

将惯导位置误差分别设置为0 m,1 m,5 m,10 m,并进行仿真。第一个整周模糊度浮点解误差如图9所示。从仿真结果可以看出,随着惯导位置误差的逐渐增大,整周模糊度浮点解误差也相应增加，但随着历元的增加,其误差也在逐渐减小。说明惯导的辅助效果与惯导自身的精度密切相关,惯导精度越高,模糊度浮点解误差越小,辅助效果越明显。

由于惯导的位置误差随时间积累,为了更好地反映动态载体运动过程中惯导位置精度对模糊度浮点解误差的影响,现根据载体的运动轨迹对惯导数据进行仿真。设两个运动载体上的惯导的陀螺仪漂移误差均为0.02(°)/h,加速度计漂移误差均为100 μg,仿真时间为200 s,仿真结果如图10所示。从图中可以看出,惯导误差随时间积累,与实际情况相符,能够真实反映载体运动过程中惯导的误差变化情况。现用该仿真惯导数据来辅助整周模糊度解算,以第一个模糊度为例,其浮点解误差如图11所示。可以看出,随着观测时间的增加,虽然惯导位置误差随时间不断积累,但模糊度浮点解误差在不断减小,并逐渐收敛至模糊度真值附近。这是由于观测历元的不断增加,观测方程之间的强相关性逐渐减弱,法矩阵的严重病态性不断得到改善,惯导误差的影响被不断削弱。这表明,在动态载体运动过程中,惯导误差的积累不会影响整周模糊度浮点解的正确解算。

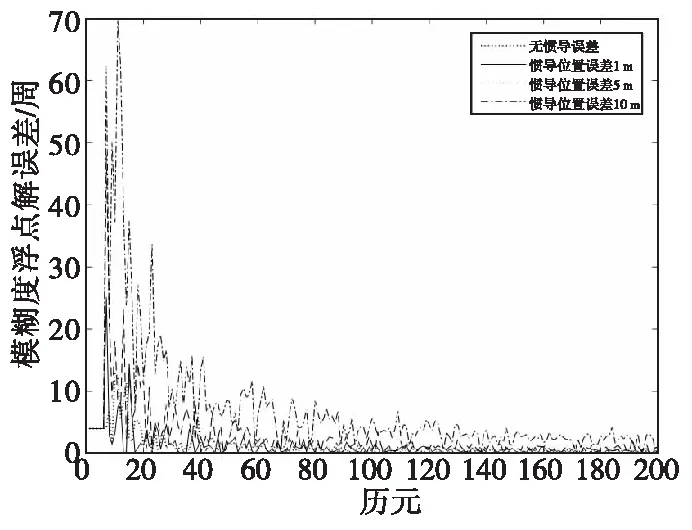
图9 惯导位置精度对模糊度浮点解误差的影响Fig.9 INS positioning accuracy influence integer ambiguity floating solution error

图10 惯导动态误差曲线图Fig.10 INS dynamic error curve

图11 惯导误差累积下模糊度浮点解误差变化情况Fig.11 Integer ambiguity error changing with the accumulation of INS error

4 结论

本文提出了惯导辅助动对动整周模糊度解算方法,该方法将惯导伪距双差与载波相位双差进行组合,构造新的观测量和观测矩阵,然后用最小二乘法以及LAMBDA算法对整周模糊度进行固定求解。仿真实验结果表明,惯性信息的辅助使得观测方程之间的强相关性有较大程度的削弱,法矩阵的严重病态性得到明显改善,整周模糊度的固定用时有较大幅度的缩短,模糊度浮点解的误差明显减小,并获得了厘米级的相对定位精度,惯导误差的积累不会影响整周模糊度的正确解算,该方法能够较好地实现动对动整周模糊度的快速解算。