分次环上的分次w-模

2019-08-27吴小英王芳贵梁春梅

四川师范大学学报（自然科学版） 2019年4期

吴小英, 王芳贵, 梁春梅

(四川师范大学数学科学学院, 四川成都 610066)

1 引言及预备知识

近年来,由于分次环在代数几何上的应用背景,分次环及分次模范畴得到极大的关注.分次投射模、分次内射模、分次平坦模、分次FP-内射模(亦称FP-gr-内射模)、分次余挠模等模类概念和分次Noether环、分次凝聚环、分次半单环和分次QF环等环类概念都相继被建立到分次环上[1-8].

乘法理想理论在刻画环的结构中发挥了重要作用.近年来,也有许多用乘法理想理论的方法来研究分次环的文献(参见文献[9-12]).用乘法理想理论的方法研究分次环,很多学者们假定G是无挠的(交换)半群,给定的分次环是整环的条件下开展工作.例如在文献[11]中证明了若G是无挠的半群,且每个齐次元素是单位,则分次整环R是完全整闭整环.

用星型算子的方法研究分次环的文献相对较少.文献[10]引入了分次v-理想I的概念,不过只是简单假定I是分次的分式理想和未分次的v-理想.相应地,文献[12]中也引入了分次SM整环的概念,仍然假定R是整环,G是无挠半群.在文献[12]中证明了关于分次版本的Mori-Nagata定理:若R是分次SM整环(R是整环,G是无挠半群,满足w-分次理想的升链条件),则R的完全整闭包是分次Krull整环.

如何把乘法理想理论的方法,特别是星型算子的方法,应用到一般的交换分次环上是需要关注的问题.对于未分次情形,w-算子首先是建立在整环上[13],2011年,Yin等[14]借助Hom函子与Ext函子把w-算子理论建立到一般的交换环上.这给我们一个很好的启发,借助于分次的HOM函子与EXT函子,完全可以去掉R是整环和G是无挠半群的假设,建立一般分次交换环上的分次版本的w-算子理论.支撑交换环上的w-算子理论需要很多基础概念,例如GV-理想、GV-无挠模与w-模等,建立一般分次交换环上的分次版本的w-模理论仍然是一个系统性的工作.本文逐步给出这些概念对应的分次版本,以及相关性质和刻画.注意无挠半群Γ可以嵌入一个Abel群G.因此,在群G-分次交换环上的研究完全包含了在无挠半群Γ-分次交换环的研究,从而本文中的关于分次w-模的结论,完全包含了文献[12]中关于分次w-理想的讨论.

HomR-gr(M,N)={f∈HomR(M,N)|

对任意的σ∈G,有f(Mσ)⊆Nσ}.

HomR-gr(M,N)中的元素称为分次同态.以分次R-模为对象,分次同态为态射构成的范畴用R-gr表示.

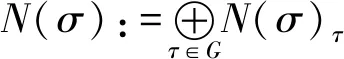
设f:M→N是R-同态,σ∈G.若对任何τ∈G,都有f(Mτ)⊆N(τσ)=N(σ)τ,则f称为次数为σ的同态.显然有f∈HomR-gr(M,N(σ)).

令HOMR(M,N)σ=HomR-gr(M,N(σ)),则

是分次R-模.

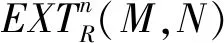
关于分次R-模M和N的张量积和其它的相关概念和符号,参见文献[15-17].

2 分次GV-理想与分次GV-无挠模

设J是R的分次理想,M是分次R-模,则包含关系J⊆R诱导一个自然分次同态

φ:M→HOMR(J,M),

更明确地

φ(x)(a)=ax,a∈J,x∈M.

相应地,M到HomR(J,M)的自然同构用φ表示.由文献[15],有下面的交换图

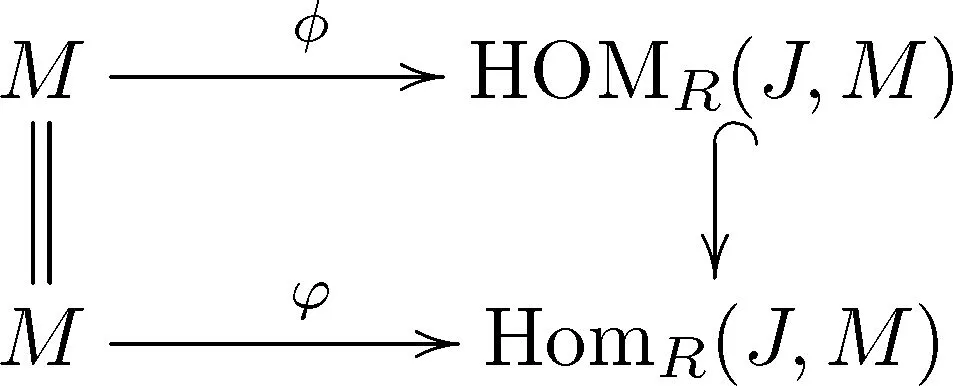
故当φ是满同态时,有

HOMR(J,M)=HomR(J,M),

且φ是分次单同态当且仅当φ是单同态.

命题 2.1设J是R的分次理想,M是分次R-模,则有:

1)φ是分次单同态当且仅当HOMR(R/J,M)=0;

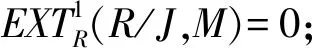
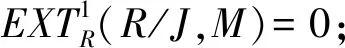
4) 若φ是同构,则HOMR(J,M)=HomR(J,M),且φ是分次同构.

证明由文献[15]中§8.5习题,有分次同构M≅HOMR(R,M).于是有下面正合列的交换图

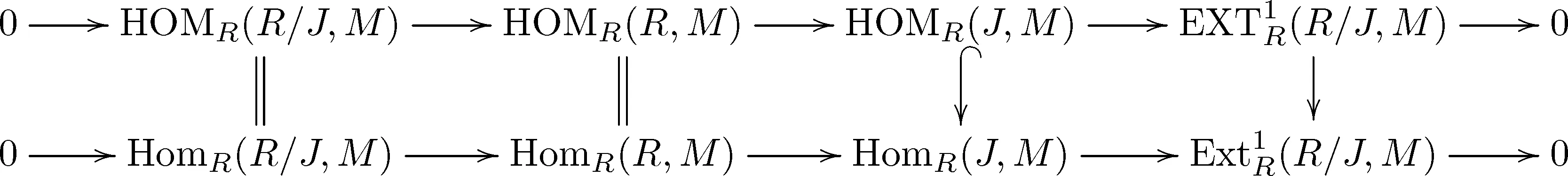
由上行的正合性即得1)～3).由上面的交换图即得4).

定义 2.2设J是R的有限生成分次理想.若自然分次同态φ:R→J*=HOMR(J,R)是分次同构,则J称为分次Glaz-Vasconcelos理想,简称为分次GV-理想,简记为J∈GVgr(R).

命题 2.31)R∈GVgr(R)；

2) 设J是R的有限生成分次理想,则J∈GVgr(R)当且仅当J∈GV(R)，于是有GVgr(R)⊆GV(R)；

3) 设J1∈GVgr(R),J2是R的分次理想,且J1⊆J2,则HOMR(J2,R)≅R.特别地,若J2是有限生成的,则J2∈GVgr(R)；

4) 若J1,J2∈GVgr(R),则J1J2∈GVgr(R).

证明1) 显然.

2) 设J∈GV(R),在命题2.1的4)中令M=R即知J∈GVgr(R).反之,设J∈GVgr(R),由下面的交换图

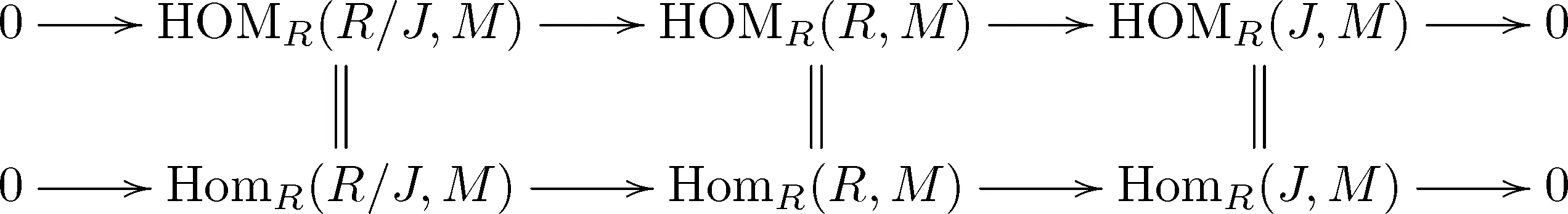
由上行是正合列知下行也是正合列,故φ:R→HomR(J,R)也是同构,即J∈GV(R).

3) 由命题2.3的2),J1∈GV(R).由文献[17]中命题6.1.9,有HomR(J2/J1,R)=0.因此有HOMR(J2/J1,R)=0, 从而

HOMR(J2,R)→HOMR(J1,R)

是分次单同态.由正合列0→HOMR(R/J2,R)→HOMR(R/J1,R)是分次正合列知HOMR(R/J2,R)=0.由下面的两行是分次正合列的交换图

4) 对任何σ∈G.分次满同态ψ:J1⊗RJ2→J1J2诱导一个分次单同态

(ψσ)*:HomR-gr(J1J2,R(σ))→

HomR-gr(J1⊗RJ2,R(σ)).

从而又诱导分次单同态Ψ:HOMR(J1J2,R)→HOMR(J1⊗RJ2,R).由分次环上的相伴同构定理(参见文献[15]中命题2.4.9)可得

HOMR(J1⊗RJ2,R)≅

HOMR(J1,HOMR(J2,R))≅HOMR(J1,R)≅R.

因此由复合分次映射

是分次同构,故Ψ还是分次满同态.于是Ψ还是分次同构,因此φ是分次同构,即J1J2∈GVgr(R).

例 2.4尽管已知GVgr(R)⊆GV(R),但仍可能有GVgr(R)≠GV(R).例如,设R=Z[x],则R可以看作G=Z分次环,其中n≥0时,Rn=Zxn,而n<0时,Rn=0.于是J=(2,x+1)∈GV(R),但是(2,x+1)不是分次理想,从而J∉GVgr(R).

设S是R的分次理想的集合,满足:1)R∈S;2) 若I,J∈S,则IJ∈S,则S称为R的一个分次理想的乘法系.由命题2.3,GVgr(R)是R的一个分次理想的乘法系.

设M是分次R-模.令

tgr(M)={x∈M|存在J∈GVgr(R),

使得Jx=0}.

命题 2.5设M是分次R-模,则tgr(M)是M的分次子模.

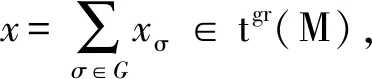
定义 2.6设M是分次R-模.若tgr(M)=M,则称M是分次GV-挠模;若tgr(M)=0,则称M是分次GV-无挠模.

命题 2.7设M是分次R-模,则有:

1) 分次模M是分次GV-挠模当且仅当对任何x∈M,存在J∈S,使得Jx=0;

2) 分次模M是分次GV-无挠模当且仅当由J∈S,x∈M,Jx=0,能推出x=0;

3)tgr(M)是分次GV-挠模,M/tgr(M)是分次GV-无挠模;

4) 分次GV-挠模的分次子模和分次商模都是分次GV-挠模;

5) 分次GV-无挠模的分次子模是分次GV-无挠模;

6) 若M既是分次GV-挠模,又是分次GV-无挠模,则M=0;

7) 对任何J∈GVgr(R),R/J是分次GV-挠模.

证明与未分次环上GV-挠模与GV-无挠模情形是对应的,也容易得到.

命题 2.8设M是分次R-模,则M是分次GV-无挠模当且仅当对任何J∈GVgr(R),自然分次同态φ:M→HOMR(J,M)是单同态,等价地,HOMR(R/J,M)=0.

证明设J∈GVgr(R),由于φ是分次单同态当且仅当φ:M→HomR(J,M)是单同态,故对φ进行证明即可.

设M是分次GV-无挠模.设x∈M,φ(x)=0,则对任何a∈J,有φ(x)(a)=ax=0.于是有Jx=0.由于M是分次GV-无挠模,故x=0,即φ是单同态.

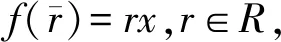
命题 2.9设M是分次模,σ∈G.

1) 若M是分次GV-无挠模,则M(σ)也是分次GV-无挠模;

2) 若M是分次GV-挠模,则M(σ)也是分次GV-挠模.

证明1) 对任何σ,τ∈G,J∈GVgr(R),由于M是分次GV-无挠模,故HOMR(R/J,M)=0.于是有

HomR-gr(R/J,M)τσ=HomR-gr(R/J,M(σ))τ=0,

从而有HOMR(R/J,M(σ))=0,即M(σ)是分次GV-无挠模.

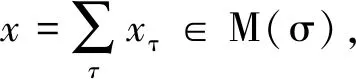
对任何分次模M,同样可以建立分次本性扩张和分次内射包的概念,参见文献[15].以下用Eg(M)表示分次模M的分次内射包.

命题 2.101)R是分次GV-无挠模;

2) 设N是分次GV-无挠模,则Eg(N)也是分次GV-无挠模.

证明1) 由命题2.8即得.

2) 记E=Eg(N).设J∈GVgr(R),证

HOMR(R/J,E)=HomR(R/J,E)=0.

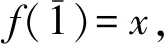
命题 2.111) 分次模N是分次GV-无挠模当且仅当对任何分次GV-挠模M,HOMR(M,N)=0;

2) 分次模M是分次GV-挠模当且仅当对任何分次GV-无挠模N,HOMR(M,N)=0.

证明1) 设N是GV-无挠模,M是GV-挠模.先证HomR-gr(M,N)=0.

设f:M→N是分次同态.对任何x∈M,由于M是分次GV-挠模,故存在J∈GVgr(R),使得Jx=0.因此有f(Jx)=Jf(x)=0.由于N是分次GV-无挠模,故有f(x)=0.因此有f=0,HomR-gr(M,N)=0.

对任何σ∈G,由命题2.9,N(σ)也是分次GV-无挠模,于是有HomR-gr(M,N(σ))=0.由此得到HOMR(M,N)=0.

假设反之条件成立,则对任何J∈GVgr(R),有HOMR(R/J,M)=0.由命题2.8,N是GV-无挠模.

2) 设M是分次GV-挠模,由命题2.11的1)知对任何分次GV-无挠模N,有HOMR(M,N)=0.

假设反之条件成立.若M不是分次GV-挠模,则T:=tgr(M)≠0,于是M/T是非零的分次GV-无挠模,从而自然分次同态M→M/T是非零同态.于是有

HomR-gr(M,M/T)≠0,

从而HOMR(M,M/T)≠0,矛盾.

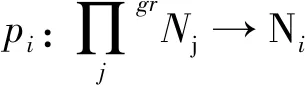
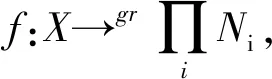
2) 有自然同构

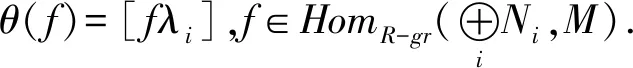
3) 有自然同构

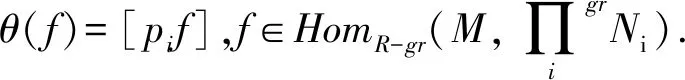
4) 对任何n≥0,有自然分次同构

与

证明1) 此即分次直积的泛性质,其证明参见文献[18]中命题2.2.

2) 显然θ是单同态.设

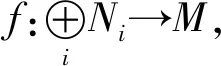
3) 亦有θ是单同态.由引理2.13的1)知θ是满同态.

4) 由维数提升方法,只要对n=0和n=1的情形证明即可.只证第一式,第二式是类似的.设σ∈G,有

另一方面,由引理2.12有

当且仅当Supp(f)=σ,当且仅当对任何下标i,fi∈HomR-gr(Ni,M(σ)),当且仅当

因此有

由2)知

故有自然分次同构

设0→M→E→C→0是分次正合列,其中E是分次内射模,则有下面的两行是分次正合列的交换图

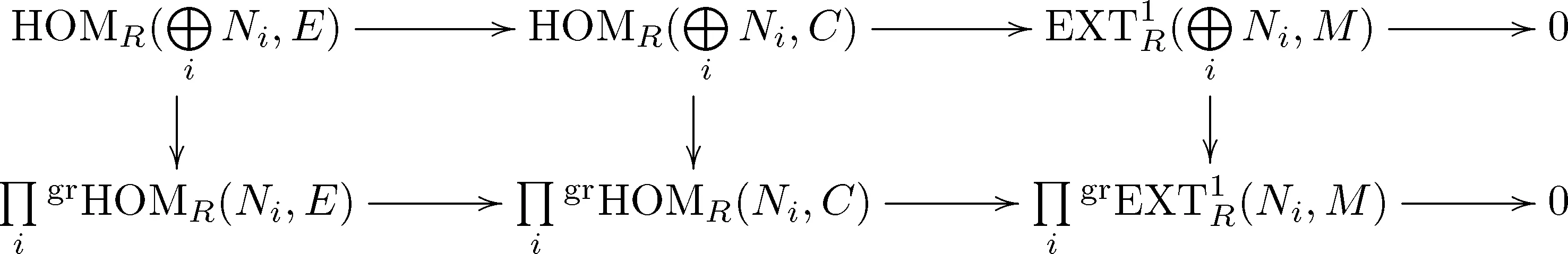
于是左端2个垂直箭头是分次同构,从而右端的垂直箭头是分次同构.

命题 2.14设{Mi}是一簇分次R-模,则有:

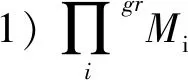
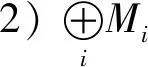
证明1) 由引理2.12与引理2.13的4)的第二式即得.

2) 设J∈GVgr(R).类似于未分次情形,有自然分次同构

由引理2.13,有分次同构

再引用命题2.1与命题2.8即得所证.

命题 2.151) 设M是分次模,N是分次GV-无挠模,则HOMR(M,N)是分次GV-无挠模;

2) 设M是有限生成分次模,N是分次GV-挠模,则HOMR(M,N)是分次GV-挠模.

证明1) 设F=⊕R是分次自由模,F→M→0是分次正合列,则有分次正合列0→HOMR(M,N)→HOMR(F,N).由引理2.13和引理2.14有

HOMR(F,N)≅∏grN

是分次GV-无挠模,故HOMR(M,N)是分次GV-无挠模.

2)F=Rn是分次自由模,F→M→0是分次正合列,则亦有分次正合列

0→HOMR(M,N)→HOMR(F,N)

以及HOMR(F,N)=Nn是分次GV-挠模.故HOMR(M,N)是分次GV-挠模.

3 分次w-模

文献[17]对交换环上的w-模理论作了系统总结,现在来定义分次环上的分次w-模.

显然分次GV-无挠的分次内射模是分次w-模.

命题 3.2设M是分次w-模,则对任何σ∈G,M(σ)也是分次w-模.

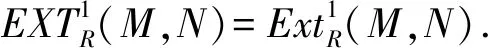
证明考虑分次正合列0→A→F→M→0,其中F是有限生成分次自由模.于是A是有限生成分次模.考虑下面的两行是正合列的交换图

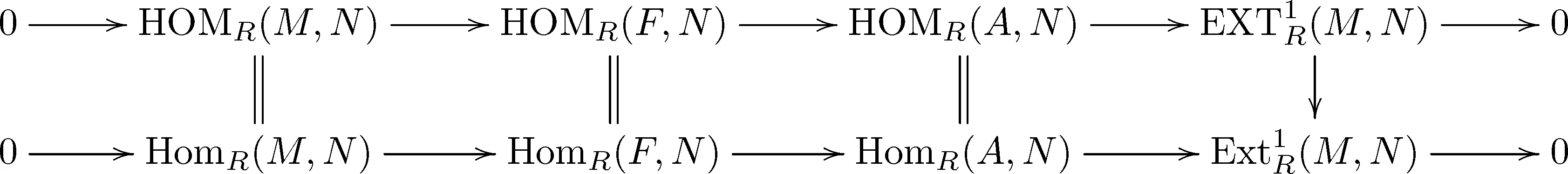
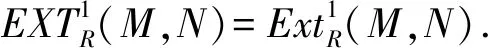
命题 3.41) 设M是分次GV-无挠模,则Eg(M)是分次w-模;

3) 分次投射模是分次w-模.

证明1) 由命题2.10,Eg(M)是分次GV-无挠模.由内射性得到Eg(M)是分次w-模.

2) 对任何J∈GVgr(R),由引理2.13,有自然分次同构

由文献[17]中定理3.9.2与引理3.3,有自然分次同构关系

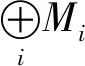
3) 显然,R是分次w-模.由命题3.4的2)知分次投射模是分次w-模.

引理 3.5设M是分次模,σ∈G.

1) 若M是分次投射模,则M(σ)也是分次投射模;

2) 若M是分次内射模,则M(σ)也是分次内射模;

3) 对任何分次模N有

证明1) 对任何分次模N有

HomR-gr(M,N(σ-1))=HomR-gr(M(σ),N).

设0→A→B→C→0是分次正合列,则0→A(σ-1)→B(σ-1)→C(σ-1)→0也是分次正合列.由下面的交换图以及上行是分次正合列

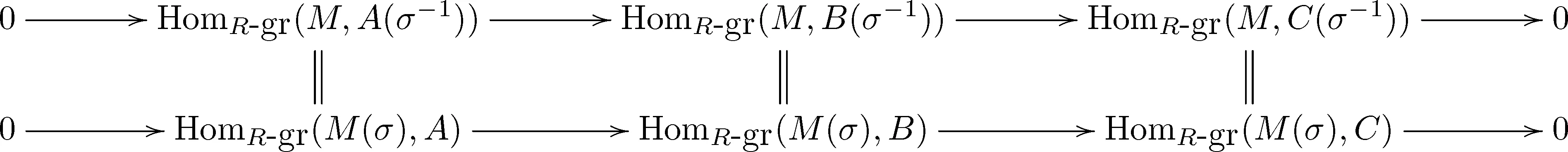
得到下行是分次正合列,因此有M(σ)是分次投射模.

2) 类似于引理3.5的1)可得.

3) 设0→L→P→M→0是分次正合列,其中P是分次投射模.由引理3.5的1),P(σ-1)也是分次投射模.从下面的两行是分次正合列的交换图

即可得证.

设M是分次模.称{Mα|α≤τ}是M的分次子模的连续升链,是指M有分次子模升链

0=M0⊆M1⊆…⊆Mα⊆Mα+1⊆…⊆Mδ=M,

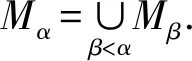
引理 3.6设T是分次GV-挠模,则T有分次子模的连续升链

0=T0⊂T1⊂T2⊂…⊂Tα⊂…⊂Tδ=T,

使得对每一序数α,Tα+1/Tα是循环分次GV-挠模.

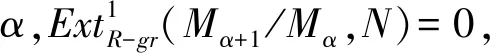
证明在文献[19]中引理1的证明中或文献[17]中引理11.7.2的证明中用分次模代替模,分次同态代替同态即得所证.

定理 3.8设M是分次GV-无挠模,则以下各条等价:

1)M分次w-模;

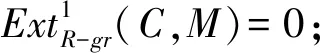
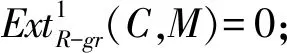
7) 对任何的J∈GVgr(R),任何分次同态f:J→M可以扩张到R上;

8) 对任何的J∈GVgr(R),自然分次同态φ:M→HOMR(J,M)是分次同构;

9) 由Jx⊆M,其中J∈GVgr(R),x∈Eg(M),能推出x∈M;

10) 设E是包含M的分次GV-无挠内射模,由Jx⊆M,其中J∈GVgr(R),x∈E,能推出x∈M;

11) 设N是包含M的分次w-模,由Jx⊆M,其中J∈GVgr(R),x∈N,能推出x∈M;

12) 对任何分次正合列0→M→N→C→0,其中N是分次w-模,有C是分次GV-无挠模;

13) 存在分次正合列0→M→N→C→0,使得N是分次w-模,C是分次GV-无挠模.

2)⟹3) 显然.

3)⟹5) 由引理3.6和引理3.7即得.

5)⟹4) 对任何σ∈G,由命题2.9,C(σ-1)也是GV-挠模,故由引理3.5有

3)⟹6) 显然.

6)⟹3) 仍设C=R/J.前面已证存在R的分次GV-理想I,使得I⊆J,且HOMR(J/I,M)=0.于是HomR-gr(J,M)→HomR-gr(I,M)是分次单同态,由下面的两行是分次正合列的交换图

6)⟺7) 与未分次情形的证明类似.

1)⟺8) 由命题2.1即得.

1)⟹11) 不妨设x∈Mσ是齐次元素.定义f:J→M(σ),f(a)=ax,a∈J,则f是齐次同态.由命题3.2,M(σ)是分次w-模.由于1)⟺7),故存在g:R→M(σ),使得g|J=f.记y=g(1),则J(x-y)=0.注意作为集合有M(σ)=M,于是y∈M.由于M是分次GV-无挠模,则有x=y∈M.

11)⟹10)⟹9) 显然.

9)⟹7) 记E=Eg(M).设f:J→M是分次同态,则存在分次同态g:R→E,使得对任何a∈J,有f(a)=g.记x=g(1),则Jx=f(J)⊆M.由假设,x∈M,于是g:J→M是f的扩张.

11)⟹12)⟹13)⟹11) 类似于未分次情形的证明.

命题 3.11设M是分次模,N分次w-模,则HOMR(M,N)是分次w-模.特别地,分次对偶模与分次自反模是分次w-模.

证明设0→A→F→M→0是分次正合列,其中F=⊕R是分次自由模.于是有分次正合列0→HOMR(M,N)→HOMR(F,N)→HOMR(A,N).由命题3.4知,HOMR(F,N)=∏grN是分次w-模.由命题2.15,HOMR(A,N)是分次GV-无挠模.由定理3.8,HOMR(M,N)是w-模.取N=R和M=HOMR(M,R),即可得证分次对偶模与分次自反模是分次w-模.

命题 3.12设M是分次GV-无挠模,则对任何齐次元素x,x∈M,ann(x)是R的分次w-理想.从而对M的任何非空子集X,ann(X)也是R的分次w-理想.

证明设J∈GVgr(R),a∈R,使得Ja∈ann(x),则Jax=0.由于M是分次GV-无挠模,故ax=0.因此a∈ann(x),即ann(x)是R的分次w-理想.

命题 3.13设M是分次w-模,N是分次GV-无挠模,f:M→N是分次同态,则Ker(f)是M的分次w-子模.

证明设J∈GVgr(R),x∈M,Jx∈Ker(f),则f(Jx)=Jf(x)=0.由于N是分次GV-无挠模,故f(x)=0.因此x∈Ker(f),故Ker(f)是M的分次w-子模.

设M是分次模,N是M的R-子模(未必是分次的).文献[15]指出,N内包含有一个最大的分次子模,用(N)g表示,即N的所有元素的齐次分量生成的分次子模.另一方面,也存在一个M的包含N的最小分次子模,用(N)g表示,即N中所有齐次元素生成的子模.

引理 3.14设M是分次模,L、N是M的子模,I是R的理想,x∈M和a∈R是齐次元,则有:

1) (I)g(N)g⊆(IN)g,(IN)g⊆(I)g(N)g;

2) (Ix)g=(I)gx,(aN)g=a(N)g.

证明1) 由(I)g⊆I,(N)g⊆N,以及(I)g(N)g⊆N是M的分次子模,有(I)g(N)g⊆(IN)g.

由于N⊆(N)g,I⊆(I)g,以及IN⊆(IN)g,得IN⊆(I)g(N)g,于是(IN)g⊆((I)g(N)g)g.由于((I)g(N)g)g是分次模,故((I)g(N)g)g=(I)g(N)g,于是(IN)g⊆(I)g(N)g.