Mg2Si0.3Sn0.7掺杂Ag和Li的热电性能对比*
2019-08-27袁国才陈曦黄雨阳毛俊西禹劲秋雷晓波张勤勇
袁国才 陈曦 黄雨阳 毛俊西 禹劲秋 雷晓波 张勤勇†
1) (西华大学材料科学与工程学院,成都 610039)
2) (西华大学西华学院,成都 610039)
1 引 言
热电材料是一种可以将热能和电能直接相互转化的功能材料.因为没有运动部件、体积小和使用寿命长,热电器件受到了人们的广泛关注.热电材料的转换效率用无量纲的优值ZT衡量,定义为ZT=σS2T/(κe+kL+kBi),其 中s,S,T,ke,kL和kBi分别表示电导率、泽贝克系数、绝对温度、电子热导率、晶格热导率和双极热导率[1−5].可见,ZT值与功率因子 (PF=sS2)成正比.一般提高功率因子的方法包括增加能带简并[6,7]、调节有效质量[8,9]、能带过滤[10,11]、提高迁移率[12]、引入共振能级[13,14]和优化载流子浓度[15−17]等.
随着化石燃料的枯竭和地球环境的日益恶化,环境友好的Mg2Si基热电材料引起了人们的广泛兴趣[18−21].通过第一性原理模拟,人们研究了Mg2(Si,Sn)[22]和 Mg2(Ge,Sn)[23]材料中载流子浓度及不同掺杂剂[24−26]对热电输运的影响.通过实验,人们发现 n 型掺杂剂 Al,La,Bi和 Sb[27−30]和p 型掺杂剂 Ga,Na,Li和 Ag 等能够有效优化Mg2(Si,Sn)材料的载流子浓度[31−34].这些研究表明,不同的掺杂剂能够显著影响Mg2Si基热电材料的热电性能.
本文在 Mg2Si0.3Sn0.7的 Mg位分别掺杂了Ag和 Li,使 Mg2Si0.3Sn0.7从 n型半导体转变成p型半导体.在对比Ag掺杂和Li掺杂的样品物性测试中发现,Li掺杂样品有较高的载流子浓度,没有出现明显的双极效应.采用Callaway模型分析电热输运表明,掺杂能增强声子散射.其中Ag原子和Li原子对样品的质量场波动散射和应变场波动散射有不同的作用.
2 实验方法
Mg2(1–x)Ag2xSi0.3Sn0.7(x=0,0.01,0.02,0.03,0.04,0.05)和 Mg2(1–y)Li2ySi0.3Sn0.7(y=0,0.02,0.04,0.06,0.08)采用 Mg 粉 (纯度 98.5%)、Li块(纯 度 99%)、 Ag 粉 (纯 度 99%)、 Si粉 (纯 度99.99%)和Sn粉(纯度99.99%)为原材料.为了补偿制备过程中Mg的缺失,Mg元素过量了5 wt.%.首先,在手套箱(氧含量和水含量均不超过0.1 ppm)中将混合均匀的原料密封在石墨坩埚中.石墨坩埚被放置于连续通入Ar气(纯度99.99%)的管式炉中进行两步固相反应,即分别在873 K和973 K加热24 h[30].获得的材料被球磨成粉末,放入直径12.7 mm 的石墨模具快速热压,并在873 K 保温5 min.将烧结的样品制备成合适的形状用于物相分析、结构表征和物性测试.
X射线衍射数据采用德国布鲁克公司D2型号X射线衍射仪(XRD)收集.微观形貌图像由美国 FEI 公司 QUANTA FEG 250 扫描电镜 (SEM)获得.采用德国耐驰公司的LFA-457激光热导分析仪测试热扩散系数D和比热容Cp,并计算获得热导率(k=DrCp),其中密度r由阿基米德排水法测得.应用日本Ulvac-riko公司ZEM-3同时测量电导率和泽贝克系数,测试温度范围均为室温至 773 K.霍尔系数RH通过范德堡 (van der Pauw)原理在1.5 T磁场中测量得到.载流子浓度根据p=1/(eRH) 计算得到,其中e为电子电荷量.迁移率根据µ=σRH计算获得.
3 结果与讨论
3.1 物相分析
Mg2(1–x)Ag2xSi0.3Sn0.7和 Mg2(1–y)Li2ySi0.3Sn0.7的XRD图谱和晶格常数如图1所示.可以看出,Mg2(1–x)Ag2xSi0.3Sn0.7和 Mg2(1–y)Li2ySi0.3Sn0.7化合物是Mg2Si和Mg2Sn组成的间隙固溶体(图1(a)和图1(c)),都有相同的反萤石立方体结构(空间点群Fm3m).掺杂Ag元素和掺杂Li元素的样品与Mg2Si0.3Sn0.7的所有衍射峰均一一对应.随着掺杂量增加,没有出现明显的第二相,也没有MgO等杂质的物相.在图1(b)中,样品的晶格常数随x含量先增加后略有降低,表明固溶Ag含量最多的样品为Mg1.94Ag0.06Si0.3Sn0.7.在图1(d) 中,除了y=0.08样品,样品的晶格常数随y含量几乎没有变化,表明固溶Li含量最多的样品为Mg1.88Li0.12Si0.3Sn0.7.
3.2 微观结构分析
图2是 Mg2Si0.3Sn0.7,Mg1.9Ag0.1Si0.3Sn0.7和Mg1.92Li0.08Si0.3Sn0.7样品的断口微观形貌图.在图2(a)—(c)中,断口的SEM显示为无孔的样品,表明样品具有较高的密度.根据阿基米德法测量的密度达到理论密度的95%以上.在图2(d)中,Mg1.92Li0.08Si0.3Sn0.7的背散射图像显示在分辨率极限内样品中元素分布均匀.这与Yin等[35]通过相同方法制备n型Mg2Si0.3Sn0.7热电材料的结果接近.
3.3 热电性能及讨论
Mg2(1–x)Ag2xSi0.3Sn0.7和 Mg2(1–y)Li2ySi0.3Sn0.7在室温的物理参数见表1.根据单抛物能带模型(SPB),输运参数表达式为[36]
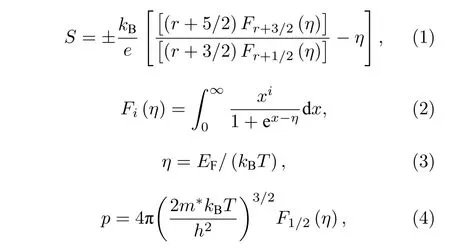
其中kB,Fi(h),h,h分别为玻尔兹曼常数、费米积分、简约费米和普朗克常数.当声学声子为主要散射机制时,散射因子r=-1/2.

图1 Mg2(1-x)Ag2xSi0.3Sn0.7(0 ≤ x ≤ 0.05) 和 Mg2(1-y)Li2ySi0.3Sn0.7(0 ≤ y ≤ 0.08) 的 XRD 图谱 (a),(c)与晶格常数 (b),(d)Fig.1.XRD patterns (a),(c) and lattice constant (b),(d) of Mg2(1-x)Ag2xSi0.3Sn0.7 (0 ≤ x ≤ 0.05) and Mg2(1-y)Li2ySi0.3Sn0.7(0 ≤ y ≤ 0.08).

图2 (a),(b),(c)分别为 Mg2Si0.3Sn0.7,Mg1.9Ag0.1Si0.3Sn0.7,Mg1.92Li0.08Si0.3Sn0.7的 SEM 图 像 ; (d) Mg1.92Li0.08Si0.3Sn0.7的背散射图像Fig.2.(a),(b) and (c) are SEM images of Mg2Si0.3Sn0.7,Mg1.9Ag0.1Si0.3Sn0.7,and Mg1.92Li0.08Si0.3Sn0.7; (d) the back scattered electron image of Mg1.92Li0.08Si0.3Sn0.7.
在表1中,未掺杂的Mg2Si0.3Sn0.7为n型半导体,掺杂Ag元素和掺杂Li元素后样品转变为p型半导体.在相同掺杂浓度时,掺杂Li元素样品的载流子浓度高于掺杂Ag元素的载流子浓度,其中主要原因可能是不同的掺杂剂Ag与Li的电离能不同[33,37].图3是Seebeck系数S与载流子浓度p之间的 Pisarenko关系图.在图3中,在Mg2(Si,Sn)和 Mg2(Ge,Sn)中掺杂 p 型掺杂剂的所有材料的有效质量大约为1.2m0.根据文献报道,在 Mg2(Si,Sn) 和 Mg2(Ge,Sn) 中掺杂 Ag,Li,Ga 和Na没有改变材料的能带结构,可以用SPB模型来描述其电热输运[32,37−39].但是,Zhang 等[33]使用两步固相法和等离子活化烧结制备的掺杂Li的Mg2Si0.3Sn0.7显示不同掺杂浓度有效质量不同.Tang等[34,40]使用熔纺和等离子放电烧结合成的掺杂Li和Ag元素的Mg2Si0.4Sn0.6的有效质量分别约为1.5m0和1m0.在本文中,采用两步固相法和热压合成的掺杂Li和Ag的Mg2Si0.3Sn0.7的有效质量约为 1.2m0.de Boor等[37]分析指出,Li掺杂的样品的迁移率发生变化主要是不同制备方法对热电材料产生的影响.Mg2(Si,Sn) 和 Mg2(Ge,Sn)不同的制备方法形成的晶粒大小、固溶区间、杂质和晶界影响了载流子的散射[18,20,21,39].此外,我们从图中仍然可以发现,多数样品的有效质量集中在1.2m0,表明 SPB模型仍然对Mg2(Si,Sn)和Mg2(Ge,Sn)有指导性作用.

表1 Mg2(1-x)Ag2xSi0.3Sn0.7(0 ≤ x ≤ 0.05) 和 Mg2(1-y)Li2ySi0.3Sn0.7(0 ≤ y ≤ 0.08)在 300 K 的物理参数Table 1.Physical parameters of Mg2(1-x)Ag2xSi0.3Sn0.7 (0 ≤ x ≤ 0.05) and Mg2(1-y)Li2ySi0.3Sn0.7 (0 ≤ y ≤ 0.08) at 300 K.

图3 Seebeck 系数S 与载流子浓度 p 之间的 Pisarenko 关系Fig.3.The Pisarenko plot between Seebeck coefficient S and carrier concentration p.
Mg2(1–x)Ag2xSi0.3Sn0.7和 Mg2(1–y)Li2ySi0.3Sn0.7的电性能与温度的关系图如图4所示.图4(a)中,Mg2Si0.3Sn0.7掺杂Ag元素后,电导率显示增加.在500 K左右,由于本征热激发而明显出现混合导电现象,电导率从随温度下降趋势转变为上升趋势.图4(d)中,掺杂 Li元素的 Mg2Si0.3Sn0.7的电导率显著增加,随着温度升高,电导率呈现下降趋势,没有出现明显的混合导电现象.在图4(b)中,掺杂Ag的样品的Seebeck系数显示为正值.Seebeck系数随着温度升高先上升后下降,在500 K左右出现显著的混合导电现象.在图4(e)中,掺杂Li的样品的Seebeck系数随着温度升高而增加.在 773 K 时,Mg1.96Li0.04Si0.3Sn0.7样品的 Seebeck系数最大值达到 169 μV/K.在图4(c)中,Mg1.9Ag0.1Si0.3Sn0.7的功率因子在473 K时达到最大值1.08×10–3W·m–1·K–2.在图4(f)中,Mg1.96Li0.04Si0.3Sn0.7的功率因子在673 K时达到最大值1.62 ×10–3W·m–1·K–2.结果显示,掺杂 Li的样品没有明显的混合导电现象,而且功率因子比掺杂Ag的样品高了约50%,这主要是因为掺Li样品具有较高载流子浓度.
图5(a)是Mg2(1-x)Ag2xSi0.3Sn0.7的热导率随温度变化的关系图.随着温度升高,Mg2Si0.3Sn0.7样品和掺杂Ag样品的热导率先降低然后显著增加.在图5(d)中,掺杂Li样品的热导率随着温度升高先降低然后呈现略微上升的趋势.根据Wiedemann-Franz法则,晶格热导率与双极热导率之和的计算方程为[41]:

其中L为洛伦兹常数,单位为 W·W·K–2.在图5(b)中,Mg2Si0.3Sn0.7样品和掺杂Ag样品出现明显的双极效应,双极热导率在高温时比室温的晶格热导率高.掺杂Ag后,双极效应温度比Mg2Si0.3Sn0.7样品的双极效应温度略有提高.在图5(e)中,掺杂Li的样品明显地提高了双极效应温度,并且显著地抑制了双极效应.在图5(c)中,Mg1.9Ag0.1Si0.3Sn0.7在623 K的最大ZT值达到0.34,比Tang等[34]的结果降低了约24%,其原因可能是Tang等掺杂Ag 样品拥有较高的载流子浓度 (6.23×1019cm–3).在图5(f)中,Mg1.92Li0.08Si0.3Sn0.7在 773 K 的最大ZT值达到0.54,比Zhang等[33]报道的结果提高了约8%.图5中的对比结果显示,掺杂Li元素能够有效抑制双极效应,并且掺杂Li元素的ZT值比掺杂Ag元素的ZT值提高了大约58%.

图4 (a)—(f) Mg2(1-x)Ag2xSi0.3Sn0.7(0 ≤ x ≤ 0.05)和 Mg2(1-y)Li2ySi0.3Sn0.7(0 ≤ y ≤ 0.08)的电导率、Seebeck 系数和功率因子与温度的关系Fig.4.The temperature dependence of (a),(d) electrical conductivity,(b),(e) Seebeck coefficient and (c),(f) power factor for Mg2(1-x)Ag2xSi0.3Sn0.7 (0 ≤ x ≤ 0.05) and Mg2(1-y)Li2ySi0.3Sn0.7 (0 ≤ y ≤ 0.08).
根据Callaway理论,如果只考虑Umklapp散射和点缺陷声子散射,掺杂样品的晶格热导率kL和未掺杂样品的晶格热导率之比可以表示为[42,43]:

这里u,θD,W,h,v和G分别是无序尺度因子、德拜温度、单位原子体积、普朗克常数、平均声速和实验的无序散射因子.根据 Slack[44]和Abeles[45]假设,无序散射因子G可表示为:

图5 (a)—(f) Mg2(1-x)Ag2xSi0.3Sn0.7(0 ≤ x ≤ 0.05) 和 Mg2(1-y)Li2ySi0.3Sn0.7(0 ≤ y ≤ 0.08)的热导率,晶格热导率和 ZT 值与温度的关系图Fig.5.The temperature dependence of (a),(d) thermal conductivity,(b),(e) lattice thermal conductivity and (c),(f) ZT for Mg2(1-x)Ag2xSi0.3Sn0.7(0 ≤ x ≤ 0.05) and Mg2(1-y)Li2ySi0.3Sn0.7(0 ≤ y ≤ 0.08).



其中ci为第i个亚点阵的原子数;是第i个亚点阵的平均质量和平均半径;是第i个亚点阵的两个不同原子的质量;是第i个亚点阵的两个不同原子的原子半径; 两个不同原子的浓度分数分别是是应力场调节因子;GM为质量场波动散射因子,GS是应变场波动散射因子.
图6是Mg2Si0.3Sn0.7的掺杂Ag和Li浓度与质量场波动散射因子GM和应变场波动散射因子GS的关系图.在图6(a)中,根据 Callaway 理论计算的掺杂Ag样品的质量场波动散射因子GM显著大于掺杂Li样品的质量波动因子GM.在图6(b)中,掺杂Li样品的应变场波动散射因子GS远大于掺杂Ag样品的应变场波动散射因子GS.结果表明,掺杂Ag降低晶格热导率主要是由于掺杂的Ag原子与Mg原子的相对原子质量相差较大,掺杂Li降低晶格热导率主要是由于掺杂的Li原子的溶解度较高.
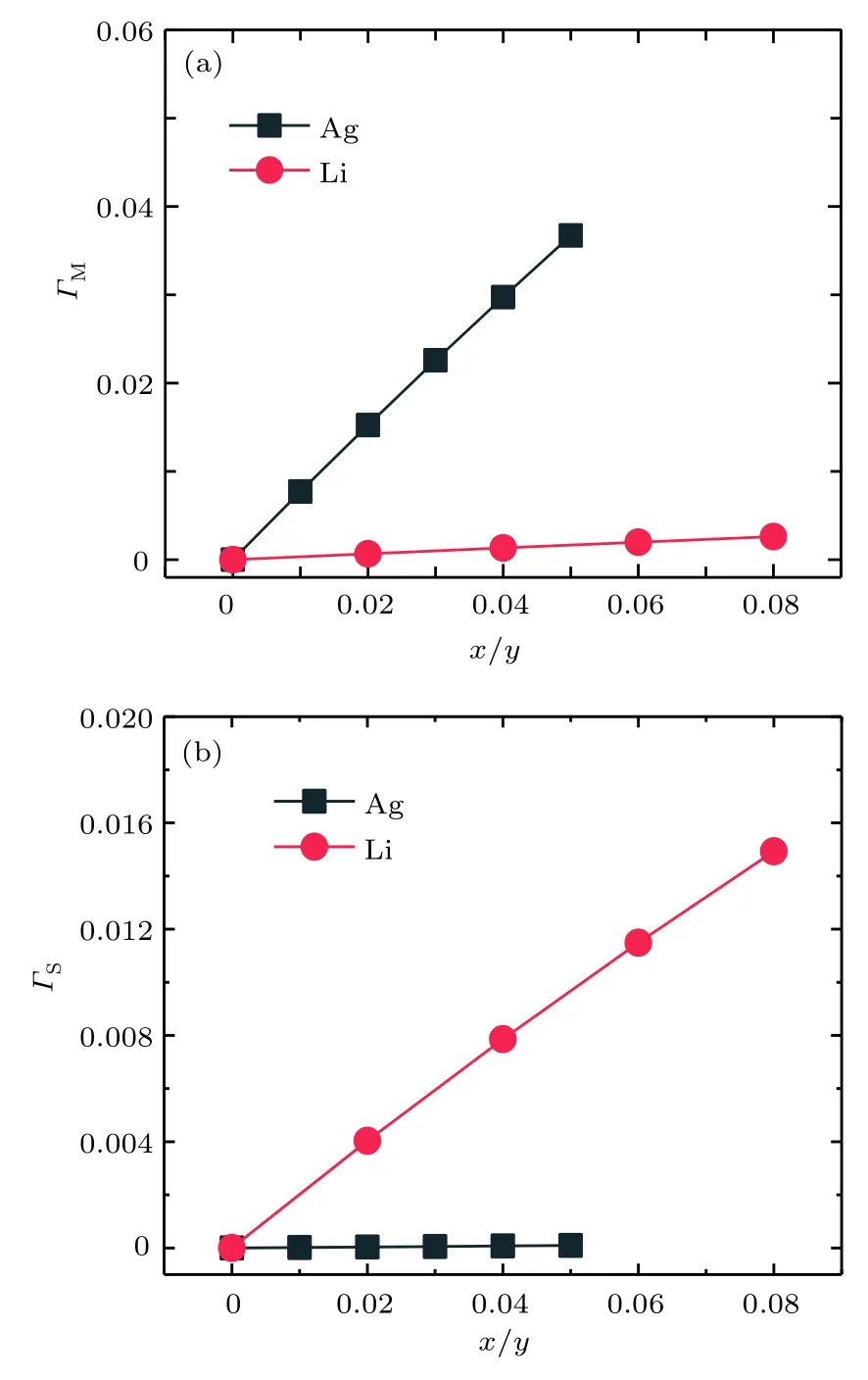
图6 Mg2Si0.3Sn0.7 的掺杂 Ag 和 Li浓度与质量场波动散射因子GM和应变场波动散射因子GS的关系Fig.6.The relation of (a) the mass fluctuation scattering parameter GM,(b) strain field fluctuation scattering parameter GS and doping Ag,Li content of Mg2Si0.3Sn0.7.
4 结 论
通过两步固相法在Mg2Si0.3Sn0.7的Mg位分别掺杂了Ag和Li元素并合成了p型热电材料.通过物相分析、微观形貌的表征和热电性能的测试,分析和对比了所有样品的热电性能.Ag和Li均是有效的p型掺杂剂,能够将n型的Mg2Si0.3Sn0.7掺杂成p型的半导体.在Mg2Si0.3Sn0.7基体中掺杂Ag和Li元素,可以有效地增加电导率,提高功率因子,最终获得优化的热电优值.但是,掺杂Li元素有较高的固溶度,能够达到较高的载流子浓度,获得较高的功率因子.同时,掺杂 Li元素的样品拥有较高的载流子浓度有效抑制了双极效应,降低了高温的总热导率.通过Callaway理论计算,我们发现掺杂Ag能够有效提高声子在质量场散射,掺杂Li元素能够有效提高声子在应变场散射.
