水处理絮凝动力学研究进展

樊 琦

(江西省水投勘测设计有限公司，江西 南昌 330029)

絮凝是水处理中最常见和最重要的水处理工艺，絮凝效果的好坏会对后续水处理工艺的负荷和最终出水水质产生直接影响[1-2]。水处理通过絮凝使水中的胶体颗粒脱稳和脱稳后的胶体聚集成大的聚集体，并且达到一定的强度，进而通过沉淀去除[3-4]。

为了更加深入地认识絮凝时胶体颗粒发生絮凝的具体过程，以便更好地控制絮凝发生的条件，充分发挥絮凝的作用，需进行动力学方面的研究。本文阐述了水处理絮凝动力学机理和模型理论的研究进展、缺陷以及未来的研究方法。

1 水处理絮凝动力学机理

水处理絮凝动力学主要着重于絮凝过程中颗粒粒径、浓度等随时间的减少过程，研究絮凝动力学就是要研究絮凝过程中颗粒状态的变化，了解数目多而体积小的颗粒如何逐步演变为数目少而体积大的颗粒，进而通过建立数学模型定量描述该变化过程[5-6]。

水处理中絮凝过程需要利用水流流动过程中的能量消耗，促使水中胶体颗粒相互接触并发生碰撞，逐步形成尺寸较大的絮体，最终达到使颗粒物沉降分离的目的[7]。国内外研究学者对水处理絮凝动力学问题进行了较为广泛的研究，得出了惯性效应是絮凝动力学致因[8-9]。颗粒之间相互碰撞的机理有3种[10-13]：由于液体分子热运动而使胶体颗粒产生布朗运动(Brownian motion，Br)引导的异向絮凝、水力和机械搅拌等外力产生流体剪切作用(Shear，Sh)引导的同向絮凝以及颗粒间沉降速度差异(Differential sedimentation,Ds)引导的差速沉降絮凝。絮凝过程中由于水流的强烈紊动，颗粒间的差速沉降作用表现得很微弱，尤其是在絮凝的开始阶段，细小颗粒的沉速很小，不同颗粒间的沉速差异也很小，因此，由沉速差异而产生的接触碰撞，在絮凝过程中一般可以忽略不计。

2 水处理絮凝动力学模型

国外学者在20世纪早期就已经开展了对絮凝动力学的研究，为了合理定量地描述絮凝动力学，提出了很多理论及絮凝动力学模型。

2.1 Smoluchowski模型

最早描述絮凝颗粒碰撞作用规律的絮凝动力学模型是1917年的Smoluchowski公式[14-15]：

(1)

同时给出了布朗运动(异向絮凝)和层流剪切(同向絮凝)的颗粒碰撞频率函数：

(2)

(3)

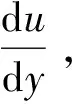
Smoluchowski假设水流所处状态为层流，碰撞只发生在两颗粒之间且均为有效碰撞；絮体一旦形成，则不会再破碎；所有微粒(包括絮体)粒径均是单分散的且均为实心球体[16-18]。这些假设均与后续的研究结果不相符，Sutherland[19]发现絮凝是簇团(若干微小颗粒聚集形成)之间发生碰撞形成的；胶体颗粒之间受静电荷斥力和范德华力影响，使部分颗粒碰撞后无法聚集，形成无效碰撞[20]。絮凝是一个絮体“生长—破碎—再生长”的过程[21-24]。另外，李振亮等[25]发现絮体颗粒粒径并不是均一分布的，且实际中的絮体颗粒并不是实心球体。Wang W等[26]在研究3种铝系絮凝剂去除腐殖酸的效率过程中，发现絮体内部存在一系列的孔隙且较大尺度的絮体同时存在多种孔道结构。

这几个假设使问题变得更简单了，但是与实际情况产生了较大偏离，所以Smoluchowski的絮凝动力学模型仅局限于层流条件下的絮凝过程，不能直接用于分析实际发生的许多絮凝现象。

2.2 改进的Smoluchowski模型

Camp和Stein[27]对Smoluchowski方程进行了修正，定义了均方速度梯度G，并用紊流的能量耗散ε与流体的运动黏滞系数ν的比值的平方根来表示紊流状态下的速度梯度，得出了紊流情况下的絮凝动力学理论公式。

(4)

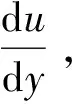
(5)

(6)

式中G——速度梯度，s-1；vi、vj——颗粒i、j的沉降速率，cm/s。

絮凝由以上三者单独或者协同作用，所以絮凝过程中的综合碰撞频率为：

β(i,j)=β(i,j)Br+β(i,j)Sh+β(i,j)Ds

(7)

Camp和Stein通过紊流絮凝速度梯度G理论，修正了Smoluchowski方程仅限于层流条件的问题，建立起了紊流条件下的絮凝动力学模型，弥补了紊流絮凝动力学理论的空白，能够很好地解释实际应用中的许多絮凝现象，至今仍是许多水处理中絮凝设计和运行的重要参数[28-30]。

该理论在得出综合碰撞频率函数时，只是对3种碰撞频率做简单的加和，忽略了3种作用之间的相互关联性[31-32]。研究表明，为使絮凝顺利进行，前期速度梯度值一般较高，后期速度梯度应逐渐减小[33-34]。而Camp和Stein公式采用整体平均G值作为控制絮凝过程的指标，并没有反映这个规律。

Du G L等[35]将分形理论引入絮凝动力学的研究，提出了分形模型下的碰撞频率函数：

(8)

(9)

(10)

式中Vi、Vj——i级和j级颗粒的体积，cm3；V0——颗粒的初始体积，cm3；ρ0、ρw——初始颗粒和液体的密度，g/cm3；DF——颗粒的分形维数。

研究表明，分形维数是絮体重要的结构参数，能够反映真实的絮体结构特征[36-37]。当颗粒的强度不变时，如果能耗增加、G值增大，则絮体的分形维数增加；反之则减小。絮凝过程应保证絮体达到一定的分形维数，同时，为了防止絮体破碎，应增加絮体的强度。所以，在絮凝前期，应保证较高的能量输入、较强的剪切强度，以增加絮体的尺度与分形维数；絮凝后期，应减少能量输入、降低剪切强度，以保证絮体强度的增加[38-39]。分形维数的引入，优化了Camp和Stein公式无法反映G值变化规律、忽略絮体破碎和重组过程的缺陷，进一步揭示了絮凝动力学的内在过程，推动了絮凝动力学的发展。但是Du G L等假设絮体碰撞前后的分形维数保持不变，与实际的絮凝动力学过程不相符。

2.3 微涡旋理论模型

Kolmogorov[40]提出了紊流的局部各向同性理论，认为紊流是由一系列大小不一的涡旋组成的涡旋运动，只有涡旋的长度尺度与颗粒粒径相近或相等时，才能最大限度地促进絮体旋转，增加与其他颗粒发生碰撞的几率，提高絮凝效果。此时，涡旋的长度尺度被称为涡旋尺度(微尺度)，在该尺度下涡旋的速度梯度最大，有利于颗粒的碰撞：

(11)

Saffman和Turner[41]在Kolmogorov理论的基础上提出了紊流碰撞频率函数：

(12)

该式形象地揭示了紊流条件下的絮凝动力学致因，能较好地描述紊流条件下的水处理絮凝过程，但是利用紊流能量耗散来描述该过程，不能揭示颗粒之间碰撞的微观本质。

Levich[42]在紊流中取一球形控制体，将颗粒的碰撞次数看作是单位时间内颗粒通过球形控制体表面进入的平均总数，最终得到了各向同性紊流条件下颗粒的碰撞频率函数，此时λ=d：

(13)

式中d——颗粒直径，cm；N——颗粒浓度，个/cm3。

微涡旋理论为后来的学者对紊流絮凝动力学的研究奠定了理论基础，但只提出了尺度与颗粒粒径相近或相等时的涡旋的絮凝作用，至于比颗粒尺寸大的涡旋对絮凝是否有贡献也无直接证据，可见该理论尚不完整。

2.4 群体平衡模型

Kumar S和Ramkrishna D等提出了群体平衡模型[43-45]，用来描述在活性污泥絮凝过程中给定尺寸的絮体数量的变化率。其模型如下：

(14)

该模型将絮凝看作是絮体聚集和破碎达到平衡的过程，可以计算出絮体尺寸大小的群体分布以及絮体强度随时间的演变过程[46]。基于该公式研究絮体聚集与破碎的絮凝动力学，取得了许多的成果。Ricardo I等[47]、Lattuada M等[48]利用群体平衡方程来描述紊流剪切流条件下的混凝动力学以及絮体聚集、破碎和重组随时间的演变关系，发现模型与实验数据具有很好的一致性。Golzarijalal M等[49]采用群体平衡模型和CFD相结合的方法，对小球藻絮凝过程中的动力学进行了研究，得到了计算微藻絮凝过程中碰撞频率和破碎率的详细模型。宋光春等[50]建立了以群体平衡模型为基本框架的水合物聚集动力学模型，对模型聚集核和破碎核的计算方法进行了选取和改进，研究结果为管道流动安全保障提供了技术支持。可见群体平衡模型的提出，为研究絮凝动力学提供了一种重要的方法，但是该模型只停留在颗粒浓度变化的层面，而没有深入揭示絮凝动力学的内在致因。各絮凝动力学模型的适用条件和优缺点对比见表1。

表1 絮凝动力学模型的适用条件和优缺点对比

除了上述絮凝动力学模型，还有许多的学者也做过相关絮凝动力学的研究。Xiang L等[51]对CPAM的聚合动力学进行了研究，发现其符合一级动力学模型。李国栋等[52]研究了絮凝过程中絮凝剂投加量对絮体结构和絮凝动力学的影响，发现絮体结构会发生重组和排列，絮体密实度会随着分形维数的增加而增加。丁进锋等[53]对PAC絮凝小球藻的动力学进行研究，通过数据拟合发现PAC对小球藻的絮凝过程符合二级动力学模型。这些学者均对絮凝动力学过程进行了探索和研究，对促进絮凝动力学的发展具有重大的意义，但是都未能提出系统的絮凝动力学模型描述絮凝过程，在今后的研究中需要引起特别关注。

3 结语

水处理絮凝动力学旨在研究絮凝时絮体颗粒的状态变化过程，国内外研究学者提出了许多模型描述絮凝动力学。Smoluchowski首先提出了胶体颗粒的絮凝动力学方程，由于做出的假设使理论与实际絮凝过程产生了较大偏离，仅局限于层流条件下的絮凝过程；后来的研究学者根据速度梯度G、碰撞频率函数β以及分型理论对Smoluchowski模型进行了改进，考虑了颗粒的分形特征，解决了该理论忽略絮体破碎与重组的问题；紊流局部各向同性理论的提出，为后来的学者对紊流絮凝动力学的研究奠定了理论基础，但由于未能说明比颗粒尺寸大的涡旋对絮凝是否有贡献，其完整性受到质疑；群体平衡模型虽只停留在颗粒浓度变化的层面，不能反映絮凝动力学的内在致因，但其为絮凝动力学的研究提供了一种重要的方法，对解释常见的絮凝现象具有重大意义。

近年来出现的絮凝动力学模型逐渐地将絮体的形态结构(数量、大小、分形维数等)以及涡旋形态大小等因素考虑在内，为进一步研究絮凝动力学的内在过程指明了方向。今后的研究需综合考虑这些因素，同时结合实际情况作出假设，才能得出能全面真实反映絮凝过程的动力学模型。