一道高三模考题的秒杀与启示

武增明

(云南省玉溪第一中学 653100)

一、试题与原参考解答

试题在锐角△ABC中，BC=2，sinB+sinC=2sinA，则BC边上的中线AD的长的取值范围是____.

这是安徽省合肥市2019年高三第一次教学质量检测理科数学试卷中的第15题，难度不大.先看命题者提供的解答.

解由sinB+sinC=2sinA，及正弦定理，得b+c=2a=4，所以c=4-b.在△ACD和△ABD中，由余弦定理，得

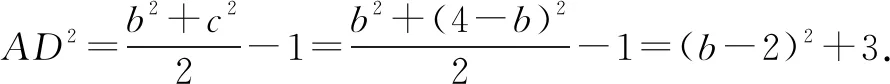
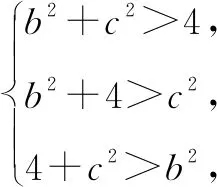
反思这种解法思路流畅，是通法，解法很朴素，但计算量较大，学生难以算对.

此题有没有更简便的解法？

二、试题的秒杀

解析因为sinB+sinC=2sinA，所以由正弦定理，得AC+AB=2BC.

三、启示

此题之所以可以秒杀，就是运用了轨迹法.什么叫轨迹法？

先研究动点的轨迹，再利用轨迹的几何性质解题，这种解题方法通常称为轨迹法.在解三角形的有关问题中，我们可以根据边或角的某种定量关系，探索出三角形的某个顶点运动的轨迹，用“形”的观点去解决所要研究的问题.这种数形结合的解题方法，使问题的求解更加直观形象，学生更容易理解接受.下面分两类例析用轨迹法求解三角形中的最值(取值范围)问题.

1.顶点的轨迹为圆或圆弧

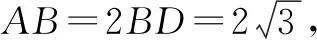
解析由题设等式及正弦定理，得a2+b2-c2=ab，故

评注本题也可设角A为x，利用正、余弦定理将CD长表示为x的函数，再利用三角函数的相关知识求得CD长的最小值，但运算量较大，而轨迹法则大大减少了运算量.一般地，在同一平面内，动点到两定点的张角度数为定值的点的轨迹是以两定点连线为公共弦、定角为圆周角的两段圆弧.

解析因为点D是动点，所以要关心的问题是，动点D在什么样的曲线上或在何区域上运动.因为∠ADB是定值120°，所以想到圆，在同圆或等圆中，同弦或等弦(同弧或等弧)所对的圆周角相等，从而动点D在圆弧上运动.

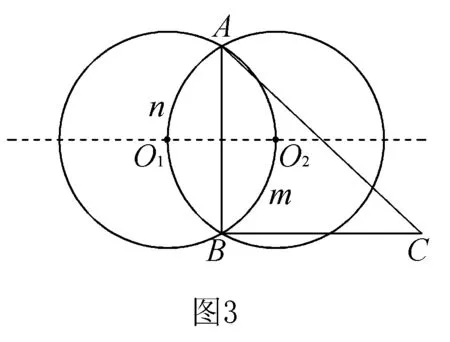
记半径为2的△ABD的外接圆的圆心在边AB左边，右边的分别为O1，O2，如图3.

评注此题用常规方法求解运算量较大，甚至很难求解.

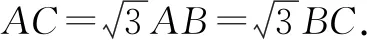
以点C为坐标原点，线段CD所在的直线为x轴建立平面直角坐标系，如图4.

以坐标原点C为极点，x轴的正半轴为极轴建立极坐标系，如图4.

动点A的直角坐标方程为(x+3)2+y2=1，化为极坐标方程为6ρcosθ+ρ2+8=0.

评注(1)在这里，可以直接求出动点A的极坐标方程.(2)在这里，若用代换法求动点B的轨迹方程，运算量非常大，几乎解不出来.用代换法，笔者没有求出动点B的轨迹方程.在此，借助贵刊，恳请同仁帮助指教.

2.顶点的轨迹为椭圆或椭圆的一部分

例4已知△ABC的内角A，B，C所对的边分别为a，b，c，面积为S，b+c=8，且S=a2-(b-c)2，求△ABC面积的最大值.

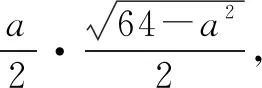
例5 如图6，线段AB=8，点C在线段AB上，且AC=2，P为线段BC上一动点，点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x，△CPD的面积为f(x)，则f(x)的最大值为____.

评注在△ABC中，若AB+AC为定值，则点A的轨迹是以点B，C为焦点的椭圆(除去与直线BC的交点)，这时△ABC就成了椭圆中的焦点三角形.

当三角形的一个顶点在一定条件下运动变化时，研究动点的轨迹是对动点运动结果的一种深刻理解.求解此类问题时，首先要明确三角形动顶点的轨迹，再利用轨迹的几何性质求最值.要做到有轨可依、有迹可循，以起到另辟蹊径、简化运算的作用.这种方法很能培养学生思维的创造性，提高学生的学习能力.