基于粒子群优化的支持向量回归车道饱和度预测

温峻峰,李 鑫,张浪文

(1.中科天网(广东)科技有限公司，广东 广州 510070;2.华南理工大学自动化科学与工程学院，广东 广州 510640)

0 引言

近年来，智能交通系统得到迅猛发展并趋于成熟。智能交通系统的运用能很好地调节交通运行，降低城市交通的拥堵程度和提高路网运行的效率[1-2]。智能交通系统是通过整合各种先进的技术，采集实时的交通数据，分析当前的交通情况，利用一定的控制方法对交通系统进行科学合理的控制[3-5]。智能交通系统的实现，需要基于对道路未来的拥堵情况的预测。

针对交通流的预测，已有诸多成果出现。裴玉龙、王晓宁利用神经网络对交通流预测模型进行了研究，分析了各种因素对交通的影响[6]。苑文江将广义神经网络应用于交通流的预测，在传统的神经网络的基础上，构造了一种新的智能神经元模型[7]。Tharam S.Dillon针对现实世界中交通流的时变性、随机性等特性，研究了智能粒子群算法[8]。赵建玉、贾磊等提出了基于粒子群优化算法的神经网络模型。该模型以神经网络为基础，提高了模型的预测精度[9]。针对交通饱和度的预测，一种基于基因遗传算法的最小支持向量回归方法被提出[10]。针对短时交通流的预测，唐智慧等提出基于交互式模型的短时交通流预测方法[11]，孙静怡等提出了考虑大型车因素的支持向量机短时交通状态预测模型[12]。

上述研究成果主要集中在对车流量的预测，而交通饱和度是对交通流量等多种交通数据的综合体现，能够很好地表征道路的拥堵状况。因此，本文通过开展车道饱和度预测建模方法研究，以期对道路未来的拥堵状况进行预测，指导合理选择出行时机，为道路间协调运行做好铺垫。该研究是实现智能交通系统的重要一环。

1 问题描述

在城市交通路网中，通过信号灯可以合理控制车流，最大化路网运行效率。信号周期对交通状况有着很大的影响。周期越长，越多的车辆能够在一个周期中通过路口，路网的运行效率也就更高。在一个控制周期内，车道运行有多种相位。在实际的交通系统中，通常采取四相位的控制方式，即整个路口车道在一个信号周期内共有四种不同的组合运行方式。相位数目的增加会使得路口交通的灵活性增加，提高路网运行效率。但相位数过多，会导致车辆等待时间过长，容易引起拥堵。

饱和度由于能够衡量在一个绿灯时间内未浪费的时间，即有车辆通过的时间与整个绿灯时间之比，因此可以表征道路拥堵状况。交通越拥堵，绿灯时车辆通过的数目就越多，相应的饱和度值也就越大。由此可见，拥堵程度与饱和度成正比关系。本文选取饱和度作为预测对象，以预测未来的交通状况。

饱和度S的计算公式为：

(1)

式中：g为绿灯时间；T为车道空闲时间；n为通过的车辆数；MF为每小时最大(即道路满载时)流量；t为车辆通过检测器的平均时间。

在已有的交通状况的预测研究中，选取折合车流量为预测对象。折合车流量CF在一定程度上能衡量交通的拥堵程度。CF的计算公式如下：

(2)

饱和度概念考虑了不同车辆型号对交通状况会产生的影响。车流量衡量的是通过路口的车辆的数目，一辆大卡车和一辆小出租车对车流量的贡献是相同的，但它们造成的交通拥堵程度不同。因此，本文开展车道饱和度预测建模方法的研究。

2 饱和度预测建模

2.1 数据预处理

作为目前先进的城市信号交通控制系统，悉尼自适应交通控制系统能对交通系统数据进行实时采集与处理，能采集相应车道的相位起始时间、相位长度、信号周期长度、车流量、绿灯时长等交通数据。基于这些原始数据，能够计算出该车道的折算饱和度。悉尼自适应交通控制系统的数据格式如表1所示。

表1 数据格式Tab.1 Formats of data

交通数据由安装在各个车道的传感器检测、采集得到，并传给中央的计算机控制系统。交通路口各项参数数据如图1所示。

由图1可知，在某些时间点，饱和度的变化非常急剧，在高峰期时段，甚至有些点的饱和度突然变为0。从实际考虑，这几乎是不可能的。这是由于硬件设施发生故障，所带来数据丢失和异常问题。本文首先进行数据进行预处理，用数据滤波方法解决数据缺失、异常等问题。

本文考察某路口前后信号周期车道饱和度如图2所示。其最大饱和度之差为50辆，纵坐标是该饱和度之差出现的频率。

图1 交通路口各项参数数据Fig.1 Parameter data of traffic intersection

图2 前后信号周期车道饱和度示意图Fig.2 Traffic lane saturation of frant and back signal cycle

由图2可知，饱和度之差为50辆对应的频率极小。考虑到在相邻的两个信号周期之间的饱和度不可能发生很大的变化，需要将出现很大的饱和度之差的点的数据剔除掉。本文剔除异常信号周期数据，并采用剔除数据前后一个信号周期饱和度的平均值代替异常点数据。数据处理结果如图3所示。

图3 数据处理结果Fig.3 Data processing results

2.2 模型输入数据的主成分分析

由于交通系统采集的数据有12种(如表1)，如果将这些数据都选为模型输入，将会使得建模极其复杂，而且可能会发生数据冗余问题，因此需要对输入数据进行选择。主成分分析法采用的是一种数据降维的思路，在原始的变量中提炼出部分关联性很弱的变量。这部分变量携带着原始变量的大部分特征。利用这部分的变量代替原始变量进行运算，可提升运算速度。

对于一个样本，有p个变量x1,x2,…,xp。则n个样品的数据矩阵为：

(3)

第一步：标准化处理。其计算公式为：

(4)

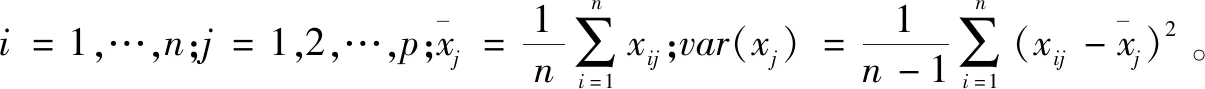
第二步：计算样本相关系数矩阵R。

(5)

经过标准化的变量的相关系数为：

(6)

第三步：用相关方法求出相关系数矩阵R的特征值(λ1,λ2,…,λp)，以及相对应的特征向量ai=(ai1,ai2，…，aip),i=1,2,…,p。

第四步：提取出能够最大程度含括原始变量数据信息量的变量。

在主成分分析中，得到的主成分的方差大小不一。这意味着它们所拥有的信息量也不相同。因此，只需要提取出拥有较大信息量的成分，剔除掉其余成分，则提取出的成分在很大程度上能代表原始变量。本文首先计算出每个成分的贡献率，通过贡献率的大小来确定主成分。其中，贡献率的计算公式如下：

(7)

贡献率可以用来衡量相应成分携带原始变量特征的比例大小。其值越大，说明该成分所携带的原始变量的特征就越多，在一定程度上更能代表原始数据。一般通过设定一个阈值来确定主成分。本文选取阈值为95%，即提取出来的变量所包括的信息量为原来的95%。

第五步：计算主成分得分。用相关计算公式计算出每个主成分的得分Fij(i=1,2,…,n;j=1,2,…,p),构成主成分得分矩阵Ψ：

(8)

第六步：根据主成分得分，选择相关参数代替原始的变量。所得到的数据保留了原始数据大部分的特征，因此可以用于代替原始变量进行分析，并且不失准确性。

2.3 支持向量回归建模

支持向量回归能够较好地解决小样本、高维数、非线性和局部极小点等实际问题。本文将采用支持向量回归方法，对交通车道饱和度进行预测建模。在线性回归中，对于一个给定的样本数据，假设其对应的最优超平面方程为：

f(x)=wTx+b

(9)

式中：f(x)为模型输出；x为模型输入；w、b为模型系数。

为了确定w，需要求解如下的优化问题：

(10)

式中：A为输入样本数据；Y为输出样本数据；ξ和ξ*为松弛变量；e为有n维数据的向量；ε和C分别是松弛因子和惩罚系数。

在实际中，采用上述线性回归方法时，精度难以达到要求。因此，引入非线性回归求解，其回归方程为：

f(x)=K(xT,AT)w+b

(11)

式中：K为核矩阵，矩阵各个元素Kij-k(xi,xj),k(xi,xj)为核函数。

使用拉格朗日乘子，将上述优化问题转换成其对偶问题：

(12)

本文先求出对偶问题的解，再利用对偶解求解出原始规划的解，最后求得回归方程。

2.4 基于粒子群优化的参数寻优

在粒子群优化算法中，每个问题的潜在解都可以看成搜索空间中的一个飞行物，将其定义为粒子。每个粒子都有着其相应的适值。该适值可以通过特定的函数计算。同时，每个粒子的属性中还拥有一个速度。该速度决定着粒子在空间里前进的速率和方向，以确定粒子的具体位置。本文根据其适值确定一个最优粒子；其他粒子根据最优粒子来调整速度，在整个空间找寻最佳的解。粒子群优化算法流程如图4所示。

图4 粒子群优化算法流程图Fig.4 Flowchart of PSO algorithm

3 模型建立与测试

通过主成分分析，本文选择折合车流量、信号周期长度、绿灯时长为模型输入。利用这些交通数据，能够直接或间接地影响车道饱和度(即交通拥堵状况)，建立饱和度预测模型，并利用粒子群优化算法对模型参数进行寻优。

选择一段时间的训练数据(包括700组输入输出数据)。首先，对该数据进行滤波。然后，基于最小支持向量机方法建立预测模型。利用该模型预测结果与实测数据相比较，给出车道流饱和度预测的对比图，说明该模型具有较好的拟合效果。车道饱和度预测结果(训练数据)如图5所示。

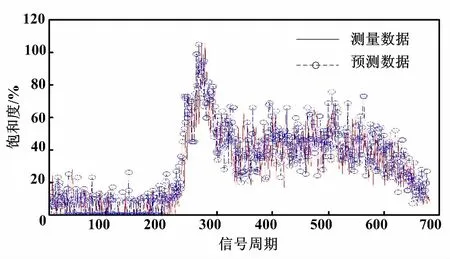
图5 车道饱和度预测结果(训练数据)Fig.5 Prediction results of traffic lane saturation (training data)

进而，本文选择另一段时间的数据，以验证所建立预测模型的有效性。测试集预测结果(测试数据)如图6所示。

图6 测试集预测结果(测试数据)Fig.6 Prediction results of the test set(testing data)

从图6可以看出，该模型对于测试集的预测精度较高，与训练集的结果相近；预测数据与实际数据的差异不大，拟合程度较高。由此说明了该预测模型的有效性。

4 结束语

本文引入实测交通数据，基于主成分分析方法选择折合车流量、信号周期长度、绿灯时长作为模型输入，对城市交通车道饱和度建立了预测模型。所建立的预测模型基于支持向量回归方法，可利用粒子群优化算法对模型参数进行寻优，并通过数据仿真验证了所提出方法的有效性。本文结果对道路未来的拥堵状况进行预测，指导合理选择出行时机，对道路间协调运行具有一定的参考意义。