大型反应堆堆芯空间控制技术发展趋势
2019-08-26方愿捷费敏锐杜大军
方愿捷,费敏锐,钱 虹,王 灵,杜大军
(1.上海大学机电工程与自动化学院,上海 200072;2.上海电力大学自动化工程学院,上海 200090)
0 引言
核能发电是能源发电的一个重要组成部分。第一批商业核电站于20世纪50年代投入运行,随后在1973年和1979年的两次石油危机刺激下,全世界的核电厂数量大幅增加[1]。截至2017年,已有超过430个商用核电反应堆在31个国家运行,装机功率约为370 GW,每年可提供超过2 400 TWh的电力[2]。核电是我国重大战略方针。在2015年国务院印发的能源发展战略行动计划(2014~2020年)列明:到2020年,核电装机容量达到58 GW,在建容量达到30 GW以上。
核电站的堆芯功率控制是核电站控制技术的核心。稳定的堆芯功率也是核电站安全运行的可靠保障。现有大型堆中因为氙反应性反馈引起的中子通量的空间振荡效应明显,整体功率控制策略相对比较保守。1904年,Ernest Rutherford提出,如果可以精准控制放射元素的分解速率,就可以从少量物质中获得大量的能量[3]。基于该思想,产生了能有效控制反应堆的空间振荡,并获得具有良好控制性能的空间控制[4]。
在小型核反应堆中,由135Xe诱导的中子通量振荡[3,5-6],可以通过适当的控制棒算法得到有效控制。然而,在物理尺寸相当于中子迁移长度很多倍的大型核反应堆中,空间振荡问题必须引起足够关注。如果忽略各位置的堆芯功率进行控制,某些部分的功率可能会超过热能上界。因此,除了利用控制技术对堆芯总功率进行控制以外,必须对各反应堆中各位置的功率进行控制[7]。
大部分空间控制的主要研究对象为加压重水堆(pressurized heavy water reactor,PHWR)[8-11]及先进重水堆(advanced heavy water reactor,AHWR)[4,6-7]。空间功率控制的核心问题在于:具有空间特征的复杂的中子动力学模型、复杂高阶非线性多参量模型的降阶简化及控制。在空间控制中,反应堆中各参量相互作用的速度差异很大,动态现象复杂,并产生了广泛分离的特征值组。大部分研究基于奇异摄动理论[1,8]。通过奇异摄动的特征值理论,将复杂的系统分解为多个子系统,先针对多个子系统进行分别设计调节器,再将系统复合,还原控制系统。文献[12]给出了奇异摄动方法在不同类型的反应堆控制问题中的应用。文献[8]将PHWR分解为1个快子系统和1个慢子系统。借鉴文献[8]的思路,文献[13]将AHWR分解成3个子系统。文献[5]将AHWR分解为1个73阶慢系统和1个17阶的快系统。
目前,国内外学者对核电堆芯的空间控制技术作了大量的研究工作[3,14-16]。本文结合以往的研究成果及最新进展,着重梳理近年来国内外核电空间功率控制技术,阐述反应堆堆芯的模型、状态空间表达、空间功率控制方法。
1 堆芯动力学模型
核反应堆模型描述了核反应堆反应过程中各参量的动态变化过程。核反应堆的功率控制可保证堆芯功率稳定运行,并保障整个核能发电过程的安全运行。堆芯内的中子动态变化会引起核电功率和温度等状态动态变化。堆芯动力学模型用于描述中子的动态变化过程,并反映反应性反馈变化的过程。
堆芯动力学的建模种类较多,适用范围也不尽相同。目前,为了便于实现控制目标,均对堆芯动力学模型进行不同程度的简化。随着研究的深入,堆芯简化控制模型从经典的集总参数模型(lumped parameter model,LPM)推广到堆芯节点模型。本文着重阐述应用于功率空间控制的堆芯节点模型。
1.1 集总参数模型
LPM是指各个参数不随空间变化而变化,使用平均值替代具有空间分布的各项参数。在实际核反应堆中,各参量都具有空间分布的特性。使用LPM实际是对控制模型的一种简化。文献[17]基于低代价的非实时/实时的核反应堆模拟器,建立了LPM。文献[18]使用集中化参数方式对一回路进行建模,使其能够在个人计算机上运行。核反应堆中子密度具有空间分布的特点。不考虑空间分布特性,使用参量(如燃料温度、冷却剂温度等参数的平均值)来替代空间分布的特征量。
包含多组缓发中子的点堆动力学模型表达式为[19]:
(1)
(2)

通常,文献中N取6,表示6组缓发中子。
由核动力工程基础知识可知,核反应堆的热功率正比于平均中子通量:
(3)
同时,反应堆热功率可以由式(4)计算获得:
(4)
式中:PTH为反应堆热功率;N0,N为额定功率时平均中子密度;PTH,N为反应堆的额定功率;φs为电子通量密度。
LPM极大地简化了控制模型,以便实现控制的设计。大量文献表明,通过线性化处理可以获得良好的控制效果[4]。LPM忽略了中子通量、各区域功率、135I浓度、135Xe浓度等分量的空间分布情形,将各参量的分布考虑为均匀在大型反应堆中,参数的空间分布特性将更加突出,使得LPM对于精准的控制存在局限性。
近年来,通过引入分数阶的概念,分数阶模型也被用于描述中子动力学模型。文献[20]对文献[21]的结果进行了推广,将模型解的数值算法转换为状态空间中的一种形式,并进行离散化。显然,分数阶模型比LPM更复杂,计算方法也更繁杂;但是分数阶模型对反应堆的物理反应过程的描述更加精确。
1.2 堆芯节点模型
大型反应堆中,多参量的空间分布无法忽略,而多参量时空表达式将进一步增加被控变量,使得控制问题更加复杂,增加了控制器的设计难度。同时,过于简化的LPM难以应用于大型堆。目前,堆芯节点模型主要针对PHWR与AHWR建立。
1.2.1 堆芯区域划分
为应用堆芯节点模型,将反应堆堆芯划分成许多小区域[22-23],小区域间的中子扩散构成区域间的耦合关系。文献[8]在一个卧式加压管式PHWR中,使用重水作为慢化剂,并将其划分成14个区域。PHWR模型区域划分如图1所示。
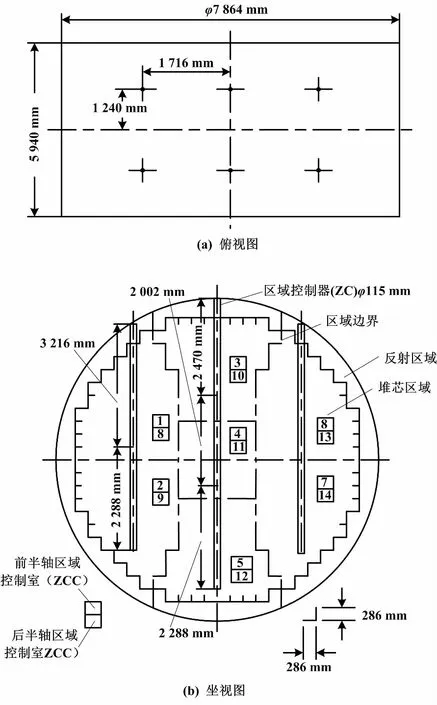
图1 PHWR模型区域划分Fig.1 PHWR model zone division
该卧式反应堆直径800 cm,长度600 cm,每个区域中心有液位区域控制器(liquid zone controller,LZC)的隔室。LZC可以控制慢化剂的液位以实现功率的分配和总功率。堆芯中分布有中子探测器检测中子通量。由式(3)可知,堆芯功率与中子通量密切相关,堆芯的功率分布和总功率可以根据各中子探测器的输出来估算[24]。
大量文献研究报道了AHWR的研究成果[25-26],并将PHWR的相关区域划分模型推广到AHWR中。作为PHWR的先进型AHWR,通常划分为17个区域[5]。AHWR模型区域划分如图2所示。AHWR与卧式PHWR不同,采用的是立式压力管式反应堆,以重水作为慢化剂。AHWR由8个吸收棒(absorber rods,AR)、8个补偿棒(shim rods,SR)、8个调节棒(regulating rods,RR)组成。其中,4个调节棒为自动调节棒,另外4个为手动调节棒。堆芯内中子通量通常由堆芯外的探测器和堆芯外的电离室测得。

图2 AHWR模型区域划分Fig.2 AHWR model zone division
1.2.2 堆芯动力学模型
经由区域划分后的加压重水堆,各区域内的参数分量被假设为不随空间变化。裂变产物氙和碘浓度及中子通量通过集总模型改写。
以下等式构成堆芯节点模型[8]:
(5)

(6)
(7)
(8)
(9)
式中:P为堆芯的功率;ρ为反应性;Ch为缓发第h组中子先驱核浓度;I和X分别为碘和氙的浓度;βh和λh分别为第h组缓发中子的分裂产量和衰减常数;Σa和Σf分别为热中子吸收和裂变截面;Eeff为每次裂变的释放能量;V为体积,下标i与j为区域的编号;σx和σI分别为氙和碘以EeffΣfiVi标准化微观热中子吸收截面;λx和λI分别为氙和碘的衰减常数;N为堆芯内区域数;m为缓发中子先驱核的组数;D为扩散系数;v为热中子速度;l为瞬发中子寿命;Aij为区域i与区域j的交界面积;dij为区域i与区域j的距离。
式(5)~式(9)在LPM基础上,增加碘与氙浓度的变化方程,同时增加了各变量的区域下标,以及区域i与区域j间的耦合系数αij。该系数取决于几何形状、材料组成和区域之间的距离。耦合系数很大程度上决定了堆芯节点模型的精度[8]。将式(5)~式(9)应用于PHWR的模型中。其中,PHWR堆芯被划分为14个区域(N=14),并在讨论空间通量不稳定性时,忽略了冷却剂、慢化剂反馈效应和温度变化等。
AHWR堆芯中子学模型如PHWR模型的式(5)~式(8),其中N=17。增加AHWR自动调节棒的运动状态方程为:
(10)
式中:H为调节棒的位置;k为自动调节棒的序号,k=2,4,6,8;v为调节棒的棒速。
堆芯节点模型的表达式,经由LPM的区域扩展,各小区域内的模型为添加了耦合系数的集总模型。借助空间区域划分,可以使得控制目标更加聚焦于各区域的功率控制。
2 状态空间表达
堆芯节点模型的状态空间均表现为非线性、高阶的特征。通常,高阶非线性系统通过在稳定状态附近线性化和奇异扰动理论,对动态模型进行简化[27]。同时,奇异摄动模型也应用于电力系统等其他场合[28-29]。
设反应堆被划分为N个区域。各区域的稳定状态下,反应性ρi0与全局反应性ρg0满足以下关系。
(11)
式中:下标0表示稳定状态;g表示全局变量。
PHWR的状态空间表达式为:
(12)
z=[δρ1,…,δρN]T
(13)
式中:δ为增量。
式(5)~式(8)改写为:
z(t)=Az(t)+Bu(t)
(14)
其中:
(15)
由式(12)~式(14)可以看出,该系统是高阶系统,状态变量由各区域的功率、中子先驱核浓度、碘和氙的浓度组成。由此可以推出:PHWR堆芯被划分为14个区域,每个区域有4个状态变量和1个输入变量。整个状态空间的维度为56维。
在PHWR基础上,文献[30]给出AHWR状态空间,状态空间可以一般性表达为:
(16)
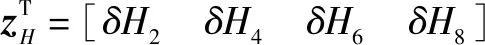

AHWR的状态空间表达为:
(17)
式中:δqf为水流量。
显然,AHWR的简化模型的复杂程度要高于PHWR模型。其控制矢量为4个独立调节棒的棒速,通过控制4个调节棒实现各区域的功率稳定控制。两者均在稳定运行点附近进行线性化,以获得简化模型[11,31]。
3 空间控制
核电站系统中,被控对象繁多。随着现代控制方法的发展,针对核电站的其他对象的控制均取得良好的控制效果[32]。但是由氙诱导空间振荡增强的控制问题仍然是当今研究的目标。通过堆芯控制抑制氙诱导振荡的增强,被称为空间控制[5]。空间控制的目标是在保证整体功率不发生氙振荡的基础上,实现各区域堆芯功率分布,以达到预期的分布效果[9]。
堆芯节点模型具有非线性和高阶等特性。通常在稳态工作点进行线性化近似,并使用奇异摄动方法对高阶模型进行降阶。即借助奇异摄动理论,根据其不同的时间尺度,将高阶系统分解成多个低阶子系统[27]。这些子系统根据极点位置进行归类,分解为快速子系统或慢速子系统。快速子系统的极点位于远离虚轴的左半平面,快速子系统能很快稳定。
控制问题归结于对各低阶子系统进行控制器综合求解,并进一步整合到整个系统的控制。
3.1 输出反馈的空间控制
基于输出的反馈控制框架,使用系统的输出作为系统的反馈量,无需花费大量计算代价估计状态变量。
在AHWR模型中,控制变量u可以分解成ug和us两个分量,u=ug+us,分别用于控制全局功率与各区域功率。在空间功率控制问题中,通常将全局输出功率yg进行反馈,即:
(18)
同样可以代入y表达式,式(18)可以改写为:
ug=-Ky
(19)
状态变量表达式为:
z=(A-BKM)z+Bus+Bfδqf
(20)
针对该输出反馈问题,设计符合需求的反馈增益矩阵K。
文献[33]针对PHWR,设计了分段定周期输出反馈控制器。其中,系统输出采样速率低于控制输入。利用奇异摄动理论分解原模型为快速子系统(14阶)和慢速子系统(42阶),分别针对慢速和快速子系统设计周期性输出反馈控制律,最终通过综合快慢子系统获得整体系统的周期性输出反馈增益。文献[34]在文献[33]的基础上,设计了快速输出采样技术的离散双重时间尺度系统控制器。这种复合状态反馈增益是通过使用快速输出采样反馈增益来实现的。文献[11]建立了一个14个输入、14个输出的新模型,通过降阶获得26阶模型,在降阶模型基础上设计周期输出反馈控制律。
上述输出反馈控制均属于多速率输出反馈,即以不同速率对控制输入和系统输出进行采样[35]。在这种方法中,输出增益是分段恒定的,控制器可以很容易地实现[36]。
3.2 状态反馈的空间控制
状态反馈通常通过状态观测器等方法对系统内部状态量进行观测。状态量的获得较为复杂,需消耗较大的计算资源。但是状态反馈直接作用于状态矢量,容易获得比输出反馈更优异的性能。
大型反应堆的堆芯时安全性有着较高要求,因此控制器必须具有较强的鲁棒性。而传统控制方法在受干扰或者参数变化时难以获得满意的性能。文献[9]设计了基于多速率输出反馈的滑膜控制器,以实现PHWR的空间控制。文献[5]将AHWR的堆芯节点模型推广到双重时间尺度模型,建模成一个慢速子系统和一个快速子系统。因为子系统中快速子系统稳定特征点远离虚轴,文献仅针对慢速子系统,设计了滑膜面与滑膜控制律。
空间功率控制的输入信号us也可以通过线性二次型方法设计实现。文献[37]~文献[38]利用降阶黎卡提方程求解了优化的反馈控制律。文献[13]将AHWR模型分解到三重时间尺度模型,并基于线性二次型方法设计了模型。AHWR的模型堆芯节点模型高达90阶,通过三重时间尺度分解方法,系统分解为慢速子系统(38阶)、快速1子系统(35阶)、快速2子系统(17阶)。状态矢量可以被划分为:
(21)
文献最终通过不同的线性二次型方法,获得稳定的全系统反馈增益,并应用于AHWR的非线性模型,在不同的不同瞬态条件下验证仿真结果。
另一类能够提升系统的抗干扰能力的控制方法是模糊控制。模糊逻辑控制(fuzzy logic control,FLC)在核反应堆控制应用中已经得较为普遍的研究[39-40]。它们可以提供对外部干扰的抵抗能力,同时可以应用于不精确的系统模型,进一步在控制系统中集成专家经验[41]。
综上所述,基于状态反馈的空间控制策略是应用系统内部状态量直接反馈到系统进行控制。堆芯节点模型的高阶特征使得状态矢量呈现高维特征,需使用奇异摄动方法对系统降阶分解,再针对不同的设计需求进行控制策略设计。随着控制技术发展,更先进的控制技术方法将逐步应用于空间控制中。
4 结束语
在第4代核电技术高速发展的背景下,核电控制的稳定性、安全性始终是核电控制的核心。核电控制策略的设计基于安全性原则。核电堆芯空间控制技术可抑制大型反应堆的氙诱导空间振荡,符合安全性期望。同时,在功率分布控制的需求上,也能够进一步实现堆芯各区域的功率控制优化,削弱了传统控制方法的保守性。
在系统模型上,针对PHWR和AHWR的堆芯区域划分与堆芯节点模型的建立已经较为成熟,堆芯节点模型的研究应当契合反应堆模型。随着技术的推进,堆芯节点模型也会随着堆型的发展而发展,会出现更先进的反应堆型。现阶段堆芯的节点模型中,仍然存在非线性、高阶等特点。如果堆芯区域划分精确,系统的阶数和状态空间的状态矢量维度均会成倍增长。系统模型的简化方法通常通过奇异摄动的方法实现,根据不同设计要求,设计成不同的多重时间尺度模型来进行模型降阶。如果模型的简化系统偏离原系统,会使得控制难以到达效果。因此,可以对兼顾模型误差的简化模型作更深一步探究。
在控制方法上,目前针对空间功率控制的方法研究主要集中在AHWR反应堆上。基于输出反馈的空间控制策略框架上更容易实现,不同采样周期与反馈速率的输出反馈控制策略已经取得较为成熟的研究成果。基于状态反馈的空间控制策略存在状态反馈高阶的问题,简化模型将堆芯节点高阶模型分解成多个快速、慢速子系统,使得控制策略设计得到简化。基于状态反馈的控制策略会消耗较大的计算代价,但其直接关联到系统的稳定性等性能;同时,可以在状态反馈的空间控制策略中应用多种智能算法及优化算法。基于状态空间反馈的控制方法具有更强的对外部干扰的抵抗能力。现有的控制技术的储备可以进一步用于研究空间控制策略。当代空间控制的研究中,还可以进一步研究各区域功率控制的优化目标,在安全性能约束下取得更优异的控制效果。
本文围绕核电站堆芯复杂模型的建模和简化的方法,介绍了堆芯节点模型及其简化方法;从输出反馈与状态反馈两个方面对空间控制技术进行介绍,并分析、归纳与总结了已有技术成果。希望本文能够为我国核电控制技术提供进一步研究的理论依据和参考。
