化“周”于形，积“长”为数——小学阶段“周长”概念建构策略初探

浙江宁波市奉化区松岙镇中心小学 汪 杰

小学阶段“周长”概念教学于三年级，它具有多个核心要素，是一个“值”更是一个“过程”。到六年级圆的周长学习后，周长与面积概念在相互依存、相互区分的过程中，终于形成各自稳固的知识结构。在这一比较长的概念学习期，笔者通过精选“原型”，夯实“过程”，多重“比较”等活动来丰富心理表征，累积活动经验，从而达到概念自动化的理解——化“周”于形，积“长”为数。

一、概念引入阶段——精选“原型”，激活经验，夯实概念表象

所谓“原型”就是某一类别的最佳正例，这个正例的关键特征越明显、越具有代表性，学生形成与概念对应的心智图像就越清晰、越准确。在概念的引入阶段，寻求生活中学生有着丰富经验的素材以及需要求出周长的情景显得尤为重要，而绕着操场跑一周，接着求出一周有多长无疑是绝佳正例。

1.从“一圈”抽象到“一周”

师：小胖要减肥，爸爸制定了一个锻炼计划，让他每天围着操场跑一圈，我们去看看他是怎么跑的（见图1、图2）。

图1

图2

在教学中，通过动画演示，激发和调用学生“跑一圈”的生活经验，让他们初步感知“边线”“封闭（起点出发回到起点）”，由此激活的生活经验在后续的复杂图形“一周”边线的辨别时，“跑”自然成了形象而有效的手段。

2.累加长度，明晰操场的周长

师：这个操场的一周到底有多长呢？

（课件依次呈现数据：直道90米—弯道110米—直道90米—弯道110米）

生：可以这样算：90+110+90+110=400米。

师：400米表示哪里的长度？

生：操场一周的长度。

师：对，400米是操场一周的长度，也可以说操场的周长是400米。今天我们就来学习周长。

正确跑出一周后，教师紧接着提出“操场一周有多长”的度量问题，通过数据连加得到操场一周长度并揭示“周长”概念，帮助学生即时形成“周长是一周的长度”这一正例表象。

二、概念形成阶段——夯实“过程”，积累经验，理解概念本质

“过程策略”表明教学不只是简单的概念的“定义”学习，而是首先让学生经历“定义化”的过程，同时积累操作活动的一般程序经验，渗透一定思想方法，最后实现过程知识与结果定义之间的融会贯通。

1.辨析一周，物化为“形”

图3

图4

学生描画一周后，呈现交通标志中间线涂色作品（见图3），予以辨析。

生1：不对，这条线是在中间的，不属于它的一周。

生2：一周是最外面的边线，这条不算。

师：想象一下，这个交通标志只留下一周的边线会是什么图形？

生：圆形。

教师演示，从实物中剥离出圆形；同理操作剥离出三角形（见图4）。

在周长概念教学中，先通过三角板和交通标志实物的描画一周，在辨析中强化“一周”的概念，接着组织学生想象并实物剥离演示，帮助学生从实物到抽象的平面图形，增进理解“一周”。

2.测量长度，累加为“数”

（1）指名学生上台测量三角形的周长，教师随机板书测量三边长度：12厘米、15厘米、12厘米。列式得到12+15+12=39厘米。

师：39厘米指的是什么呢？

生：三角板的一周长度。

（2）测量圆形的周长。师生讨论达成共识“需要借助软软的尺子测量”后，教师演示：把线绕圆一周然后缓慢打开，拉成一条线段。组织学生测量这条线段，测得长度为52厘米。

师：这52厘米表示的是什么？

生：交通标志图的一周长度。

“长度是量出来的”“周长是一周边线长度的累加”——在三角形周长度量测算中，学生首先经历的是测量，三边长度累加计算等系列过程，由此学生经历了三角形周长本质的由来；同理，在圆的周长测量活动中，教师有效渗透了化曲为直的方法，体会到圆的一周边线长度等同于一条线段的长度。

3.回顾过程，概括概念

师：同学们，刚才我们通过研究，得到400米、39厘米、52厘米，那这些数表示的都是什么呢？

生：400米是操场一周的长度，39厘米是……

师：回顾一下，这些一周的长度我们是怎样得到的呢？（课件先抽象出一周，再呈现数据和算式）

生：量出来的。

师：量所有的线？

生1：不是，先找到一周，例如三角形就只需要量一周的三条线。

生2：量好后，还要把几条线段的长度加起来。

回顾操场、三角形、圆形一周长度的研究过程，过渡到“图形一周都有固定的长度”，抽象到图形的周长。教师组织学生回顾过程，最后用生动简练的语言归纳为“先跑一周，再测量求和”。

4.辨析反例，精准概念

课件依次呈现矩形、三角形、圆形、角等图形，组织辨析以上有无周长后，教师板书周长完整概念。

师：现在你觉得“周长”的“周”指的是什么？“长”呢？

生1：周指的是一周，长指的是长度。

生2：连起来就是“一周的长度”。

生3：像三角形这样的一周有好几条边的，那就可以说成“一周的长度加起来”。

概念的精准便于学生记忆与提取，对周长概念的再加工，能够让学生望文生义，在以后遇见时能一次次主动触发已有的经验。

三、概念应用阶段——多重“比较”，重组经验，联结概念网络

比较是一种思维的过程，也是一种教学的策略。通过相似、相近数学材料的比较、分析，配合动作、语言、图像、符号等多重表征，可以消除概念间的互相混淆，从而有效把握数学定义的本质。

1.（三年级上册周长概念学习第一课时） 比较练习

A.谁测量的是周长呢？

（1）量身高

（2）量腰围

B.这两个图形周长一样吗（见图5）？（动态演示图形组合）

图5

A组习题学生通过实际的测量活动，发现虽然量的都是长度，但身高实质是一条线段的长度，而腰围是一周曲线的长度，进一步突显“封闭”“一周边线”的概念核心要素。B组习题引导学生再一次经历求周长的活动，初步感知大小并不是决定周长长短的关键因素，使其更深刻地认识周长的本质“一周边线的长度总和”，凸显了先确定一周的“形”，才能进行计算求出长度总和的“数”。

2.（三年级下册正方形面积公式学完后） 求正方形的周长和面积

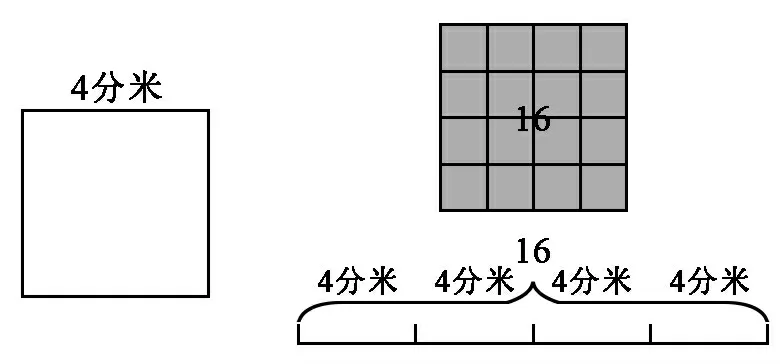
图6

生：周长4×4=16分米 面积4×4=16平方分米

师：怎么算式都是4×4=16？他们的意思一样吗？能用图表示你的想法吗？

教师在师生的交流修正中依次呈现图6，并组织学生用语言表达想法：周长是4条长4分米的线段累加成为16分米的线段；用面积为1平方分米的单位摆，一行可以摆4个，一共4行，所以面积是4×4=16平方分米。

师：那如果边长是a呢？

生：周长就是4个a累加成的一条线段的长度；面积就是一行摆a个，可以摆a行，一共a×a个。

通过同一图形周长与面积算式比较，教师首先让学生自主地用图表征算式，这个过程需要提取原有周长概念图像，是对概念一次修正和完善的过程；其次图与图之间的比较，借助数形结合，经历一维的长度累加与二维的面积累加过程，两种概念间的差异性因比较而深刻；最后运用语言及符号表征，回顾周长与面积获得的过程，以及运用现有的心理表征对公式再识别。

同理，在探究图形面积公式时，关于周长的知识也需要不断“点击”。例如，学习平行四边形的面积时，可让学生大胆猜测，呈现“邻边之和乘2”的错例，通过拉动平行四边形学具，让学生体验平行四边形周长不变而面积在变。

3.（六年级上册圆的认识单元复习时）求出图7阴影部分的面积和周长

图7

生1：用割补法后就变成了一个半圆，面积是3.14×52÷2=39.25cm2（媒体动态呈现割补最后留下半圆）。

生2：周长是3.14×10÷2+10=25.7cm

生3：不对，你算的是半圆的周长，图7周长明显比半圆长。

师：有不同想法了，谁对谁错呢？怎么验证？

生4：先跑一周，再一段一段比就可以了。（学生比画，达成共识）

师：那它的周长该怎么计算呢？

生5：大圆周长的一半加上两个小圆周长的一半。

生6：两个小圆周长的一半就是一个小圆的周长，再加大圆周长的一半。

生7：这3条圆弧的长度和，就是一个大圆的周长。(学生鼓掌)

师：做了这题，你现在有什么新的收获呢？

生8：把面进行“割”与“补”，其图形变了面积不变。

生9：如果图形的周长不变的话，只能割补它的一周边线。

在周长概念的应用过程中，教师调动了学生对周长概念的心理表征，去比较、去辨别等积变形后周长是否发生了改变，这样的活动能大大降低思维定式带来的副作用，同时还让学生对已有的知识和经验进行了必要的超越。例如，累加边线长度的经验，以往的累加更多的是一种计算求和，而现在改造为边线累加成新的图形的边线，大大提升了思维含量，更有助于学生抽象及空间想象能力的提升。