干扰条件下的雷达动态威力范围仿真方法

徐鹏，王振华

(空军预警学院，湖北 武汉 430019)

0 引言

现代战争中雷达作为重要的作战单元之一，对战争的胜负起着至关重要的作用。研究雷达作战威力范围的仿真对雷达组网、干扰突防、敌机预警等诸多方面具有现实意义。目前Matlab和OpenGL是国内外专家学者用于雷达探测威力仿真的主要软件。文献[1-3]中利用了Matlab软件对多种环境下的雷达威力范围进行了仿真分析，文献[4-7]中利用了OpenGL对复杂环境中的雷达威力范围进行了可视化仿真。但上述文献中研究的仿真背景在时间上都是静态的，无法使绘制的三维雷达威力图随着时间变化而连续、动态地显示。

美国图形分析公司研制开发的系统仿真工具包(system tool kit,STK)是目前世界航天领域最专业的三维可视化仿真软件，广泛应用于航空航天、雷达、电子对抗以及信息对抗相关多领域的仿真分析[8]。本文针对文献[4-7]的缺点，以STK仿真平台为基础[9]，通过添加Matlab插件[10]的方法实现对雷达三维威力范围的动态仿真。仿真结果表明，该方法能够在STK环境下对雷达的探测威力进行有效的动态显示，能够为作战部署提供直观的仿真场景，更有利于作战指挥员作出清晰的判断。

1 Matlab插件功能及编程逻辑

STK中的Matlab插件提供了一种可将用户自定义的模型导入STK中进行计算的功能，可实现Matlab对STK现有功能的扩展。用户可在任意的仿真时间执行自定义的数学计算模型。通过创建Matlab插件把目标模型定义为STK中仿真时间的函数，然后利用这个新的函数模型实现对STK场景显示的动态控制。

STK在使用插件时能且仅能同时调用一个插件模型，所有Matlab插件共享工作空间环境。由于STK对Matlab插件接口进行了限制，所以STK提供的每种插件都有非常具体的功能，每个Matlab插件都必须遵循相同的语法[10]：

function[output]=Matlab_Plugin(input)

switch input.method

case′register′

%定义输入/输出参数模块

case′compute′

computeData=input.methodData;

%计算输出模块

otherwise output=[];

end

上述语法中，2个百分号位置为必须定义的模块。第1个百分号位置对应输入、输出参数定义模块，其针对实现功能的不同，采用不同的输入、输出参数；第2个百分号位置对应用户自定义的计算模块。在Matlab工作区输入/输出参数是一个字符串形式的结构体，当转换到计算模式时，从computeData中提取输入参数用于计算输出的数据。

STK调用Matlab插件主要有以下几个步骤：

Step 1： 启动STK仿真软件，选择STK中需要调用插件的模块，将其工作模式改为插件模式。

Step 2： 编写自定义插件模型，定义Matlab工作环境中的输入参数，通过模型计算得到的输出数据返回到STK中。

Step 3： 通过返回数据，产生数据报表并进行三维可视化显示。

Step 4： 判断仿真时间是否结束，若未结束则返回Step 2，重新定义输入参数，如此循环。

STK软件的插件调用模式流程框图如图1所示。

2 压制干扰下的雷达对抗数学模型

2.1 干扰条件下雷达威力范围模型

雷达威力范围是指雷达通过发射和接收电磁波，能够在三维空间内探测到目标的最远距离所形成的闭合空间，在此空间内的任意点都能够被雷达有效探测。干扰条件下，干扰型无人机(以下简称干扰机)以其主瓣指向雷达，而雷达则以主瓣指向目标，一般来说干扰机与被掩护的目标不在一起，所以通常干扰机的干扰能量从雷达天线的副瓣进入雷达。雷达对抗空间示意图如图2所示。

假设雷达天线主瓣所在的方位角为θ，取θ=0～360°，ξi为干扰机在雷达平面极坐标系上的方位角，θi为θ与ξi之间的夹角，即θi为水平面上第i部干扰机与雷达的连线同雷达主瓣中心线之间的夹角，可以得到自由空间的干扰方程[11]：

(1)

式中：Pt为雷达发射的峰值功率;Gt为雷达天线的发射增益;Kj为满足功率准则的干扰压制系数,即当发现概率为Pd=0.1时，雷达接收机外端的干扰信号与回波信号功率之比;σ为雷达散射截面积(radar cross section,RCS);n为脉冲积累数;L为雷达自身的系统损耗因子；Pji为第i部干扰机的发射功率；Bn为雷达接收机带宽；Bji为第i部干扰机发射带宽；γji为第i部干扰机的干扰信号对雷达天线的极化损失，当采用圆极化时γji=0.5；Rji为雷达到第i部干扰机的距离；Lji为第i部干扰机的系统损耗因子；Gt(θi)为雷达天线对第i部干扰机干扰信号的接收增益；φi为干扰机主瓣与干扰机到雷达连线之间的夹角，通常为了追求干扰效能、节约干扰资源，干扰机主瓣应对准雷达;Gji(φi)为第i部干扰机天线在雷达方向上的增益。

为了能够真实地反映垂直面上干扰机与雷达主瓣间的夹角对雷达探测威力的影响，将天线在垂直面上的方向性函数进行修正，公式为[12-15]

(2)

式中：K为增益修正系数，通常取0.04～0.1；δ为干扰机在雷达极坐标系下的俯仰角，δ0.5为雷达天线的垂直波束宽度；φ为雷达天线在俯仰角上的波束指向。修正后，干扰条件下的雷达三维探测威力表示为

(3)

2.2 干扰机航迹模型

干扰机对雷达实施干扰时，为了节约干扰资源、最大效率地利用干扰机能量，通常将干扰机主瓣尽可能地对准雷达方向，使得能够进入雷达接收机的干扰功率达到最大。干扰机飞行航迹示意图如图3所示。

如图3所示，干扰机飞行航迹主要有4个阶段组成，分别为出航阶段、过渡阶段、干扰阶段和返航阶段。出航阶段是指干扰机从发射经过爬升直至出航完成的一段飞行路径；过渡阶段是指干扰机在进入施放干扰轨道前的一段调整路径；干扰阶段即为干扰设备开启、执行干扰任务的往复飞行路径；返航阶段是指干扰任务完成后，回收干扰机的飞行路径。这里主要对执行干扰任务阶段的飞行路径进行研究建模。由式(1)可知，在干扰机其他参数不变的情况下，飞行航迹仅会对雷达与干扰机之间的距离Rji和干扰机主瓣偏离雷达方向的角度φi产生影响。以目标雷达为坐标原点建立平面直角坐标系，干扰阶段航迹示意图如图4所示。

第i部干扰机进入干扰阶段后，沿跑道形航迹飞行并施放雷达干扰信号。干扰机经过渡阶段后从A点进入往复飞行的干扰阶段，沿逆时针方向回到A点形成一个完整的干扰周期。B，C，D，E为干扰机的状态转化点，判断状态转化点位置的条件是φi=φi0.5/2。干扰机从A点开启前向天线，到达B点时关闭前向天线，到达C点时开启后向天线，到达D点时关闭前向天线，到达E点再次开启前向天线，如此循环往复地对目标雷达进行干扰。可知干扰机在弧BC和弧DE上时，干扰设备处于关闭状态。

图4中r为干扰机的转弯半径，S1为A点到y轴的直线距离，S2为直道距离。当干扰机在直道上飞行时，设干扰机匀速飞行且速度为v，干扰时长为t，令干扰周期T=(2S2+2πr)/v，t0=(tmodT)，mod表示取余，可以得到Rji,φi与t的关系为

(4)

当干扰机在第1个1/4圆弧轨道上时，干扰机与雷达的几何关系图如图5所示。

可以得到：

(5)

同理，经化简，可以得到在干扰阶段的任意时间点的φi和Rji：

(6)

(7)

3 仿真分析

仿真思路：

Step 1: 编写STK天线增益模式的Matlab插件。定义插件的输入、输出参数及插件语法架构。

Step 2: 利用Matlab插件对雷达三维威力范围进行采样。方位角从0°～360°，按一定的采样步长，得到M个采样点；同理对俯仰角进行采样得到N个采样点；对时间维按照仿真步长进行采样得到K个采样点。那么在四维空间上的任意一个采样点的雷达最大探测距离可表示为R(θm,φn,tk)，其中1≤m≤M，1≤n≤N，1≤k≤K，共有M×N×K个数据点。

Step 3: 完成STK三维雷达威力场景构建。首先编辑干扰机飞行路径并为雷达站添加Radar模块，切换到Antenna选项，选择Antenna Script模式；然后加载Step 2中生成的Matlab插件；随后选择3D Graphics中的Attributes选项并在Volume Graphics中勾选show volume(显示体积)和show as wireframe(显现线条)；最后在Gain Scale中填入适当的距离参数，完成三维雷达探测威力范围的显示。

Step 4： 利用Matlab插件对干扰机的干扰时序进行控制，利用STK图表对压制干扰条件下雷达的探测概率进行分析。

以典型搜索警戒雷达为例，其参数设置如表1所示。假设雷达天线在垂直方向上的归一化方向函数为

fy(φ)=sin(2πcos(φ/90))sin(πcos(φ/90)/2).

(8)

对典型干扰型无人机，其参数设置如表2所示。

表1 雷达参数设置Table 1 Parameter settings of radar

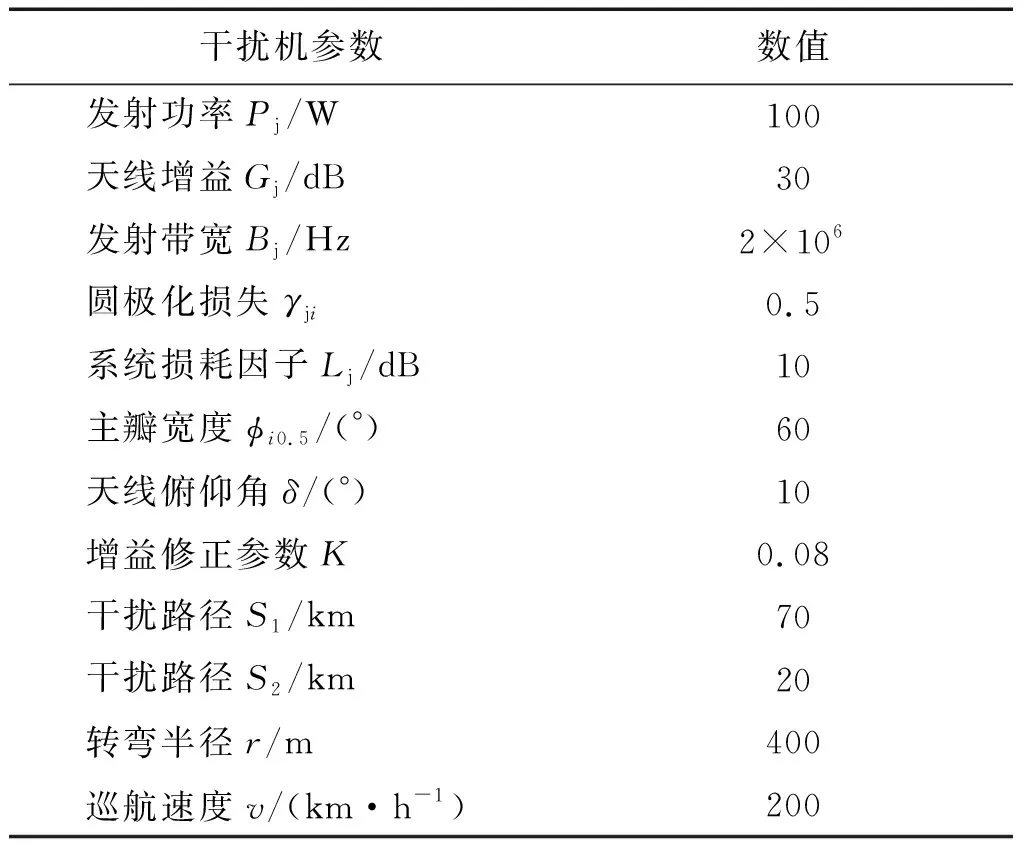
表2 干扰机参数设置Table 2 Parameter settings of jammers

综合式(1),(3)和(8)可以得到动态雷达威力范围的数学模型为

(9)

仿真1： 单部干扰机对单部雷达进行干扰，干扰机从ξ=0°方向对雷达进行干扰，仿真时间为04:00～06:00，仿真步长为30 s。单部干扰机干扰条件下的雷达三维威力图如图6所示。

结合图6a),d)可以看出，在无干扰条件下雷达的威力范围为顶部存在凹陷的规则椭球型。这是由于在水平方向上雷达的最大探测距离相同；而在垂直方向上，雷达的最大探测距离随着天线垂直方向图的变化而变化，在俯仰角接近90°时，天线的垂直方向图函数急剧减小，形成图形上的凹陷，即雷达的顶空盲区。对比图6b),c)可知，干扰机与雷达之间距离越近，压制效果越好。

仿真2： 2部干扰机同时对雷达进行干扰，干扰方向分别为ξ1=0°和ξ2=30°，仿真时间为04：00～06:00，仿真步长为30 s，第2部干扰机出发时间比第1部滞后2 min。2部干扰机联合干扰条件下的雷达威力图如图7所示。

对比图7b),c)可知，c)中干扰机UAV1的干扰设备处于关闭状态，而b)中2部干扰机同时对雷达进行干扰，2部干扰机对雷达探测威力的压制在空间上形成了叠加，使得压制角度更大，能够为进攻飞机形成更有效的保护；图7b),d)中雷达威力范围压制缺口的不同主要是由于2部干扰机到雷达间的距离不同引起的。

仿真3： 在上述实验的基础上，为雷达对抗场景添加1架F-14战斗机作为突防飞机，以检验雷达在干扰条件下的探测概率。雷达对抗场景如图8所示。

图8中，干扰机1进入干扰阶段后，突防飞机从起飞区域起飞，正对雷达飞行，拟对雷达进行“硬摧毁”，设置突防飞机的RCS为1 m2，通过Matlab插件对干扰机发射功率进行动态控制，当干扰机转弯时设置干扰功率为0 W。通过STK中的“Report”功能得到雷达在无干扰、仅有干扰机1干扰和双机同时干扰条件下对突防飞机的探测概率，仿真步长为30 s，如表3所示，表中只显示了干扰机1进入转弯阶段前后的5 min。

仿真时间探测概率(无干扰)探测概率(干扰机1)探测概率(双机干扰)04:41:000.997 1980.098 8940.036 26204:41:300.997 8180.088 6240.032 35004:42:000.998 1400.078 7920.028 43504:42:300.998 2180.998 2180.114 89704:43:000.998 0340.998 0340.096 80704:43:300.997 4420.997 4420.078 21604:44:000.998 2270.121 3780.023 26304:44:300.996 4080.118 9640.016 17204:45:000.995 3720.110 5740.010 168

为了更加直观地对比表格中的数据，干扰条件下的雷达探测概率对比图如图9所示，显示时间为10 min。

结合表3和图9可以看出，2部干扰机同时进行压制干扰能够有效弥补单部干扰机在转弯过程中无法实现有效干扰的弊端，STK强大的建模分析功能能够为演习或实战中的雷达对抗提供有力的辅助分析手段。

4 结束语

建立准确直观的三维动态可视化雷达探测威力图，对于电子战中雷达对抗场景的仿真至关重要。本文针对传统的雷达威力范围仿真方法在时间上是静止的缺点，以STK仿真平台为基础，提出了一种基于Matlab插件的动态可视化仿真方法并推导出了干扰条件下雷达动态探测威力的数学模型。通过仿真实验证明了该方法的可行性和有效性，为下一步建立更加贴近实战的雷达探测威力仿真提供参考。然而，该仿真方法的显示速度受限于数据采样算法和计算机硬件条件。