IMM-SCKF算法在海面扩展目标跟踪中的应用
2019-08-26于泽祥蔡宗平杨剑卫浩
于泽祥,蔡宗平,杨剑,卫浩
(火箭军工程大学,陕西 西安 710025)
0 引言
在传统的低分辨雷达研究中,雷达目标均被假设为点目标。而目前高分辨雷达对目标的探测能力提高[1],不但可以探测目标的距离、角度等运动量测信息,还可以提供目标更多的特征信息[2-5],例如目标的宽度和大小等形状信息。将这些扩展信息融入目标的建模中,形成扩展目标(extended object)模型。通过对扩展目标的跟踪技术展开研究,可以更加准确地实现对目标的跟踪,尤其是实现对目标部位级的探测和识别。
机动目标在不同机动过程中运动形式会发生变化,为了获得更高的目标跟踪精度,需要使滤波所采用的运动模式与目标的运动状态相匹配[6]。目前通常采用交互多模型(interacting multiple model,IMM)算法来实现目标运动状态的匹配[7],但是传统IMM算法通常采用卡尔曼滤波(Kalman filter,KF)算法对目标状态进行更新,在处理非线性非高斯问题时性能较差,难以取得较高的滤波精度。近年来提出的粒子滤波(particle filter,PF)算法[8]通过大量的采样点解决了这一问题,但是算法本身的计算量非常大,所以系统的实时性较低,在实际应用中受到限制。
近年来相关学者提出通过容积点来计算非线性近似中的概率积分,得到容积卡尔曼滤波(cubature Kalman filter,CKF)算法,其实现简单,较EKF算法具有更好的非线性估计性能[9],而且可以扩展成平方根容积卡尔曼滤波(square cubature Kalman filter,SCKF)算法,避免了复杂的矩阵分解和求逆运算,提高了数值稳定性和滤波精度[10]。文献[11]将CKF滤波与交互式多模型结构相结合,提出了IMM-CKF算法。但是目前的研究仍是将目标视为质点,没有考虑扩展信息对改善目标运动参数估计精度的影响[12-13]。
针对上述问题,本文首先参考文献[3],将海面舰船目标建模为椭圆形的扩展目标,以充分利用其特征信息,并构建出扩展量测模型。其次,采用IMM-SCKF算法对扩展目标进行跟踪滤波,通过扩展信息提高算法对海面机动目标的跟踪精度。理论分析和实验结果都表明,本文提出算法的估计性能和稳定性要明显优于传统的质点算法。
1 目标的运动模型
考虑一般非线性系统
(1)
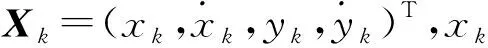
海面运动目标在运动过程中状态变化较为缓慢,所以通常采用以下2种匀速模型对其运动状态进行建模:
(1) 匀速直线运动(constant velocity,CV)模型,采样间隔为T,状态方程为
Xk=F1Xk-1+Wk-1,
(2)
式中:
(3)
(2) 匀速转弯运动(coordinated turn,CT)模型,角速度为ω,状态方程为
Xk=F2Xk-1+Wk-1,
(4)
式中:
F2=
(5)
2 扩展目标量测模型
用椭圆形来表示海面舰船目标,并且假设舰船的速度方向与椭圆模型的主轴方向一致,如图1所示。k时刻高分辨率雷达可以测量其顺向距离记为L(φk)和横向距离记为W(φk),φk为椭圆的长轴与观测雷达视线方向的夹角。
由文献[14],椭圆模型的顺向距离以及横向距离可以通过目标的尺寸参数表示为
(6)
(7)
(8)
式中:l为椭圆形模型的主轴长度;γ为椭圆形模型的长短轴比,通常情况下γ<1。在实际应用中,目标的尺寸参数可以通过目标的图像信息获取[15]。
如图2所示,在物镜O的焦平面AB处放置一个半径为r的光环,通过反光镜可以看到目标CD,调节光环半径,使其包围目标边缘,此时环的“直径角”与目标视角θ相同。通过CCD的最小分辨率(一个像素点)来度量目标的尺寸参数,可得目标的长度l为
(9)

在上述情况下,如果目标测量长度与目标真实长度不同,即目标投影不能真实反映目标长度,其误差表示为
(10)
(11)
式中:
(12)
(13)
式中:rk为目标的距离量测;θk为目标的方位量测。从以上的系统模型以及目标运动模型能看出,系统的状态方程均是线性,而观测方程均是非线性。综合来看,本文所要解决的雷达跟踪目标的问题仍属于非线性滤波问题。
3 IMM-SCKF算法
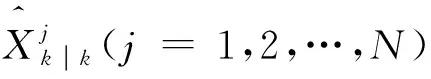
IMM算法中的滤波器通常采用卡尔曼滤波器,只有在状态模型为线性条件下才能取得较好的效果。将SCKF算法用于IMM框架,便可处理非线性模型的滤波问题。
3.1 状态估计的交互过程
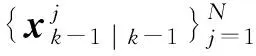
模型i转移到模型j的Markov转移概率Ptij为
(14)
交互作用后r个滤波器在k时刻输入为
(15)
式中:
(16)
计算协方差
(17)
(18)
3.2 模型修正
采用均方根容积卡尔曼滤波器,根据输入值得到状态估计和协方差估计的更新值。以其中一个滤波器为例,对于n维状态,构造2n个容积点实现积分的数值逼近,即
(19)
式中:相应的容积点和权值为
(20)
式中:[1]=[In×n,-In×n],In×n表示n维单位矩阵,[1]i是[1]的第i列向量。
(1) 时间更新
Sk-1|k-1=sqrtm(Pk-1|k-1),
(21)
(22)
(23)
(24)
(25)
式中:Tria为对矩阵的转置进行QR分解运算,然后取R阵中的非零方阵。SQ,k-1为系统噪声方差Qk-1的开方,且有
(26)
(2)量测更新
(27)
Zi,k|k-1=h(Xi,k|k-1),
(28)
(29)
(30)
Szz,k|k-1=Tria([γk|k-1,SR,k]),
(31)
式中:SR,k为量测噪声方差Rk的开方,且有
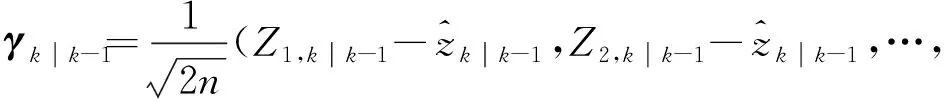
(32)
(33)
式中:
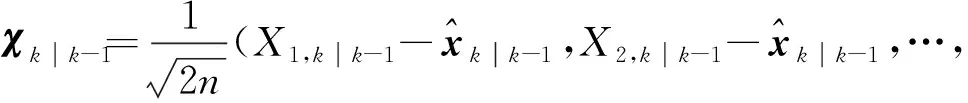
(34)
(35)
(36)
Sk|k=Tria([χk|k-1-Kkγk|k-1Kk,SR,k]).
(37)
3.3 模型概率更新
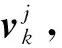
(38)
模型j的概率更新为
(39)
(40)
3.4 交互输出
k时刻的状态估值及协方差值表示为
(41)
(42)
4 仿真对比与性能评估
4.1 实验场景
下面仿真分析椭圆形模型的扩展信息对跟踪性能的影响。假设有一部位于坐标原点的高分辨率雷达对目标进行跟踪,采样时间间隔T=1 s。目标的初始位置为(100,20) km,初始速度为(100,0) m/s。目标在0~20 s,40~60 s,80~100 s时间范围内作匀速直线运动;在20~40 s内作ω=1.8 rad/s的匀速转弯运动;在60~80 s内作ω=-1.8 rad/s的匀速转弯运动。图4给出了目标的实际运动轨迹。
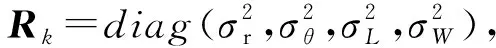
4.2 仿真结果
在上述仿真场景下做100次蒙特卡罗仿真,将传统点目标IMM-SCKF算法与扩展目标IMM-SCKF算法进行仿真实验比较。图5为扩展目标形态跟踪仿真结果,可以看出目标以椭圆模型的形态出现,仿真过程可以反映出目标的形态轮廓。
图6为传统点目标IMM-SCKF算法仿真过程中各模型的概率变化曲线,图7为扩展目标IMM-SCKF算法的模型概率变化曲线,图8为2种算法的位置均方根误差(root mean square error,RMSE)和速度RMSE对比。
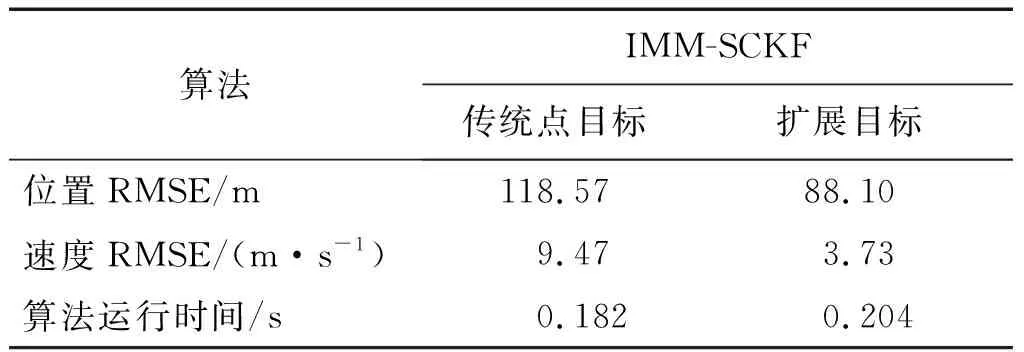
表1给出了2种算法的统计数据对比,进一步比较了2种算法的滤波性能。仿真结果表明,本文提出的扩展目标IMM-SCKF算法跟踪效果要优于传统点目标IMM-SCKF算法,具体表现在:
(1) 模型概率更接近实际情况,模型切换速度更快。从图6和图7可以看出,扩展目标IMM-SCKF算法滤波过程中的模型概率曲线更加接近真实模型概率;同时在t=20,40,60和80 s时,目标发
算法IMM-SCKF传统点目标扩展目标位置RMSE/m118.5788.10速度RMSE/(m·s-1)9.473.73算法运行时间/s0.1820.204
生机动,模型概率能更快地切换到真实模型,因此本文提出的算法在跟踪实际目标运动模型方面的性能要优于传统点目标IMM-SCKF算法。
(2) 跟踪精度更高。从图8可以看出无论是位置还是速度,本文提出算法的均方根误差都小于传统算法,表1统计数据也验证了该结论。从表1的数据中可以得到,位置跟踪误差减小了25.7%,速度跟踪误差减小了60.6%。
5 结束语
随着雷达分辨能力的不断提高,可以探测到目标更多的特征信息,然而目前的目标跟踪研究主要是将目标视为质点模型,对目标扩展量测信息的利用较少,对提高跟踪的精度有着很大的限制。为了解决这个问题,本文设计了基于IMM-SCKF算法的海面机动扩展目标跟踪方法。首先将目标的尺寸参数引入量测向量,继而建立起扩展目标模型,然后采用IMM-SCKF算法对扩展目标进行跟踪滤波,提高扩展信息对改善目标运动参数估计精度的影响。机动目标跟踪仿真结果看出,在模型切换和跟踪精度上,本文所提算法相比于现有的质点算法具有更好的效果。
