水质中8 种有机氯农药的测量不确定评定

路艳芳

（上海市岩土工程检测中心，上海 200436）

在化学分析中，测量不确定度评定成为检测和校准实验室必不可少的工作之一。其可以更科学准确的表述测量结果、建立量值溯源。本文依据不确定评定过程[1-3]，参考方法GB7492-1987[4]结合实际操作，进行不确定评定。

1 试样制备

摇匀水样，量取250mL 水样，置于分液漏斗中，加入25mL 石油醚。排气，振摇5min，静置分层，萃取液经无水硫酸钠，浓缩氮吹至约1mL,经活化好的弗罗里硅柱净化后，氮吹定容至1mL，上机分析。

2 数学模型

有机氯农药计算公式：式中：ρ为品中的目标物含量，μg/L；ρi为仪器直读目标物的浓度，μg/L；V1为浓缩定容体积，mL；V 为量取水样体积，mL

3 不确定度来源

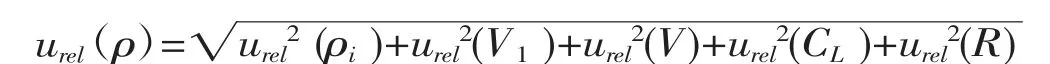
根据数学模型分析，其相对合成不确定度为：式中：urel(ρi) 为标准曲线拟合引入的不确定度；urel(V1)为浓缩定容过程中引入的不确定度；urel(V)为量取样品体积引入的不确定度；urel(CL)为配制标准溶液过程引入的不确定度；urel(R)为测量重复性引入的不确定度。

4 不确定度分量的量化

本文不确定度计算过程以α-BHC 为例，其他参数计算过程同理。

4.1 量取水样体积引入的不确定度

温度：实验室温度变化为±3℃，20℃时水的膨胀系数2.1×10-4℃-1，设其为矩形分布，则由此引起的不确定度为：

体积校准：250mL 量筒容量允差：±2.0 mL[5]；设三角分布，则由量筒引起的不确定度为：

4.2 浓缩定容引入的不确定度

温度：温度变化为±3℃，20℃时石油醚的膨胀系数1.5×10-3℃-1，设其为矩形分布，则由此引起的不确定度为：

体积校准：1mLA 级容量瓶容量允差：±0.010mL[5]；设其为三角分布，则由容量瓶引入的不确定度为：故浓缩定容的不确定度为：

4.3 配制标准溶液过程引入的浓度不确定度

1）标准物质的不确定度。

参看标准物质证书，置信水平95%，知各参数标准物质的浓度为（单位：mg/L）：α-BHC：100.8±0.55，γ-BHC：98.51±1，β-BHC：99.5±1.01，δ-BHC：102±0.24，p,p’-DDE：100.4±0.24，o,p’-DDT：100.4±1.02，p,p’-DDD：99.5±1.5，p,p’-DDT：99.47±1.01)。

以α-BHC 为例，取包含因子k=2，则标准物质引入的不确定度为：

urel（ρ1）=0.55/100.8/2=0.0028

2）100μL 移液器量允差为±2.0μL[6]，按三角分布估计，微量注射器引入的不确定度为。

温度变化引起的不确定度在此可忽略不计。

3）配制标准溶液定容至1mL，由此引入的不确定度评定过程同4.2，故在此不作罗列。其不确定度为：

则以α-BHC 为例，将上述分量合成得到标准溶液配制的不确定度：

4.4 测量重复性引入的不确定度

量取6 份250mL 水样，测定质量浓度均为0.20μg/L，按照样品制备，测定结果为（单位：μg/L）：

α-BHC：0.158，0.160，0.158，0.149，0.158，0.150 γ-BHC：0.173，0.176，0.173，0.163，0.173，0.166 β-BHC：0.217，0.221，0.219，0.207，0.220，0.215 δ-BHC：0.169，0.173，0.171，0.162，0.172，0.167 p,p’-DDE：0.184，0.188，0.183，0.175，0.184，0.178 o,p’-DDT：0.187，0.192，0.193，0.179，0.185，0.181 p,p’-DDD：0.195，0.198，0.191，0.186，0.194，0.186 p,p’-DDT：0.167，0.172，0.167，0.159，0.165，0.160

以α-BHC 为例，可计算6 次测定浓度的平均值：ρ_x=0.156μg/L，标准差：

4.5 标准曲线拟合引入的不确定度

曲线质量浓度点为（单位：μg/L）：10.0，50.0，100，500，1000，标曲点峰面积为：

α-BHC：152.8，757.8，1552.9，9281.1，19948.0 γ-BHC：145.4，717.0，1445.6，8347.5，8347.5 β-BHC：82.1，372.2，697.7，3483.3，7251.2 δ-BHC：153.4，721.3，1457.5，8506.3，18344.0 p,p’-DDE：120.7，564.5，1135.8，6622.1，14264.0 o,p’-DDT：44.0，260.8，545.2，3336.1，7540.7 p,p’-DDD：117.0，551.5，1081.9，6069.5，12734.0 p,p’-DDT：49.9，318.7，691.7，4601.7，10505.0

采用最小二乘法拟合标准曲线得到线性回归方程（强制过零点），各参数的线性方程和相关系数如下：

α-BHC：Y=19.63ρ，0.9993；γ-BHC：Y=17.69ρ，0.9994；β-BHC：Y=7.19ρ，0.9998；δ-BHC：Y=18.04ρ，0.9993；p,p’-DDE：Y=14.03ρ，0.9994；o,p’-DDT：Y=7.35ρ，0.9985；p,p’-DDD：Y=12.60ρ，0.9997；p,p’-DDT：Y=10.21ρ，0.9980

以α-BHC 为例，由标准工作曲线产生的不确定度，按下式计算：式中：S(A)为标准曲线的剩余标准差；p 为样品测定次数，p=6；n 为曲线上质量浓度点的点数，n=5；ρx 为样品中α-BHC 的平均质量浓度，0.156μg/L；ρ 为系列标准工作溶液α-BHC 质量浓度的平均值，μg/L。

5 合成不确定度

因各分量互相独立不相关，以α-BHC 为例，则合成标准不确定度为：

同理，其他参数的合成标准不确定度为：

γ-BHC：0.052，β-BHC：0.028；δ-BHC：0.053；p,p’-DDE：0.052；o,p’-DDT：0.080；p,p’-DDD：0.038；p,p’-DDT：0.088。

6 扩展不确定度

取包含因子k=2，置信水平约为95%，以α-BHC 为例，则扩展不确定度为：

U=ku(ρ)=2×0.0083μg/L=0.017μg/L

同理，可计算出其他参数的扩展不确定度。

7 结果和讨论

1）从分析过程可知，测量不确定度主要来源于标准溶液配制和标准曲线拟合过程中引入的不确定度，其他因素的影响相对较小。

2）测量重复性引入的不确定度，涵盖了人、机、法、料、环等各方面因素，在此可考虑环境和被测物质的稳定来降低其不确定度；标准曲线拟合过程中引入的不确定度，可通过增加标曲点，或者配制成被测量接近标准曲线重心的曲线，来降低不确定度。