利用SAS软件PROC MCMC过程步实现诊断性试验的贝叶斯Meta分析

许佩华 郑建清

诊断性试验最常报告的结局指标是敏感度和特异度，其中敏感度反映的是正确诊断疾病或状态的概率，而特异度反映正确识别其误诊的概率。诊断性试验的Meta分析可以定量地总结相似的原始研究，获得各个研究的汇总效应值[1]。研究结局的Meta分析可以使用固定效应模型或随机效应模型进行，前者假设研究间差异仅源于抽样误差，后者假设研究间差异不仅源于抽样误差，而且还来自研究之间未知的真实差异。对于随机效应荟萃分析，最常用的统计方法是双变量随机效应模型(BREM)和层次综合受试者工作特征(HSROC)模型[2-5]。

Meta分析可以基于频率论(经典)方法或贝叶斯方法实现。频率论认为概率是重复事件(假设)发生的频率；贝叶斯方法认为概率是数值的可信程度[6]。换句话说，频率论认为模型参数是固定的，数据是随机的；贝叶斯认为模型参数是随机的，数据是固定的。贝叶斯统计学与经典统计学在统计推断的理念和方法上存在本质上的区别，包括对信息的利用，对未知参数θ的解释以及统计推断理念上的差异等[7,8]。Rutter和Gatsonis最早提出了用于诊断性试验Meta分析的贝叶斯HSROC方法，并且可以使用免费统计软件WinBUGS实现[5, 9]。然而，利用SAS软件实现贝叶斯分析的文献较少被报道。

Menke编制了一套基于SAS PROC MCMC过程步的Meta分析代码，可以实现诊断性试验的贝叶斯Meta分析[10]，本文对其进行了介绍，并结合实例介绍SAS代码的实际应用。有关贝叶斯统计方法的理论基础，张天嵩等[8]在《高级Meta分析-基于Stata实现》一书中已有详细介绍。

1 Meta分析模型简介

1.1 诊断性试验BREM模型简介 BREM是广义线性混合模型的特例[3]。在诊断性试验的Meta分析中，原始研究提供了2×2表格数据，从而可以计算出相应的敏感度和特异度。对于研究i，TPi、FPi、FNi、TNi分别代表试验i内的真阳性、假阳性、假阴性和真阴性。RPi=TNi+FPi表示研究i中金标准试验检测出的阳性结果(RP)。RNi=TNi+FPi表示研究i中金标准试验检测出的阴性结果。

则TPi和RPi，TNi和RNi构成二项式分布[10]：

TPi～Binomial(RPi,πA,i)；TNi～Binomial(RNi,πB,i)(公式1)

公式中，πA,i是研究i待估计的真实敏感度(概率)。πB,i是研究i待估计的真实特异度(概率)。 灵敏度和特异度的BREM由下面的公式给出[11]：

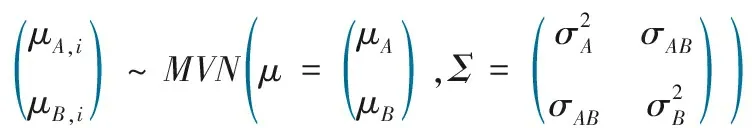
其中μA,i=logit(πA,i)，表示研究i待估计的真实敏感度的logit转换值。μB,i=logit(πB,i)表示研究i待估计的真实特异度的logit转换值。logit(π)= log(π /(1-π))表示概率π的logit转换。

1.2 诊断性试验HSROC模型简介 HSROC模型由Rutter等提出，是对综合受试者工作特征曲线模型(ROC)的扩展，该模型利用灵敏度和特异度这一常用配对指标对多个诊断性试验进行综合评价[5]。该模型具体如下：

假设研究i中某一患者疾病状态j的阳性概率为πij，其中j=0表示无病，j=1表示有病，则灵敏度PAi=πi1，特异度PBi=1-πi0。基于灵敏度和特异度，HSROC模型为：

水平1(研究内)：logit(πij)=θi+αiXijexp(-βXij)

2 资料与方法

2.1 示例数据介绍 以发表的关于高分辨率超声诊断颞下颌关节盘前移位的准确性研究为例，文章直接报道了基于HSROC 统计模型的结果[12]，采用的统计软件是STATA 12.0。张天嵩等介绍了有关HSROC在诊断试验Meta分析中的应用及Stata实现[13]。作为对比，本文提供了SAS软件的计算结果。

采用文后附录代码1录入示例数据(表1)，并将数据集存储在“file_data”。数据集“file_bidata”将数据集将file_data分成每个研究的2个记录，并添加变量“A_pos”和“B_neg”，分别识别敏感度和特异度，构建双变量数据(表2)。

需要注意的是，本文模型拟合假设诊断正确例数服从二项式分布，故无需对数据集中零事件数的研究进行校正。

2.2 SAS代码介绍 本文提供的附录代码包括数据集的录入及贝叶斯双变量随机效应Meta分析的实现。本文利用SAS软件PROC MCMC过程步编制了BREM的程序代码，并提供了HSROC模型相关的参数计算。BREM的公式2可以用SAS 9.4中的PROC MCMC实现(见附录代码)。SAS PROC MCMC的详细信息在联机手册中提供。基于随机效应模型的SAS代码(附录代码3)主要介绍如下。

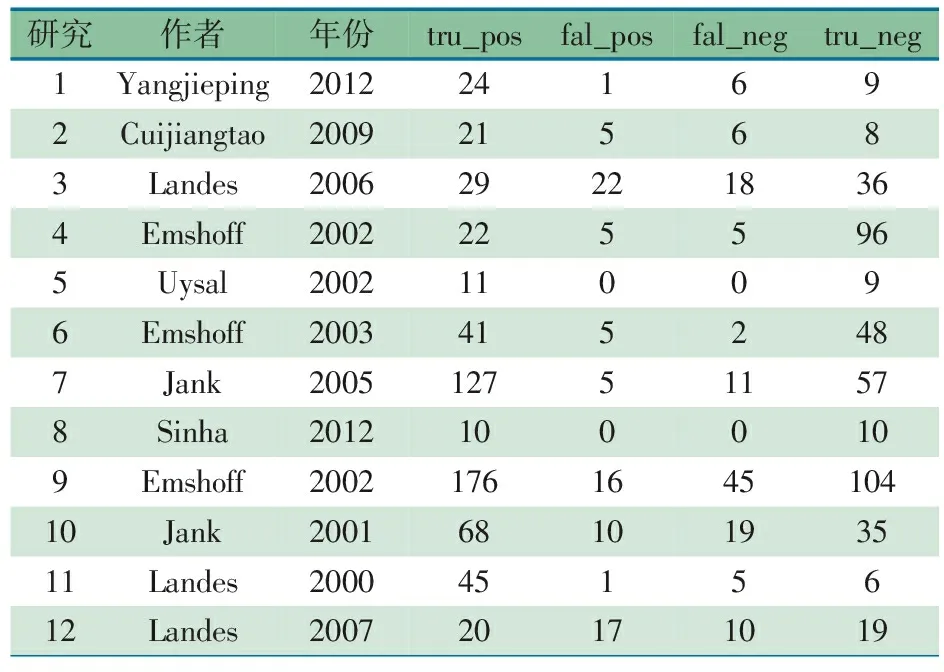
表1 待分析数据集

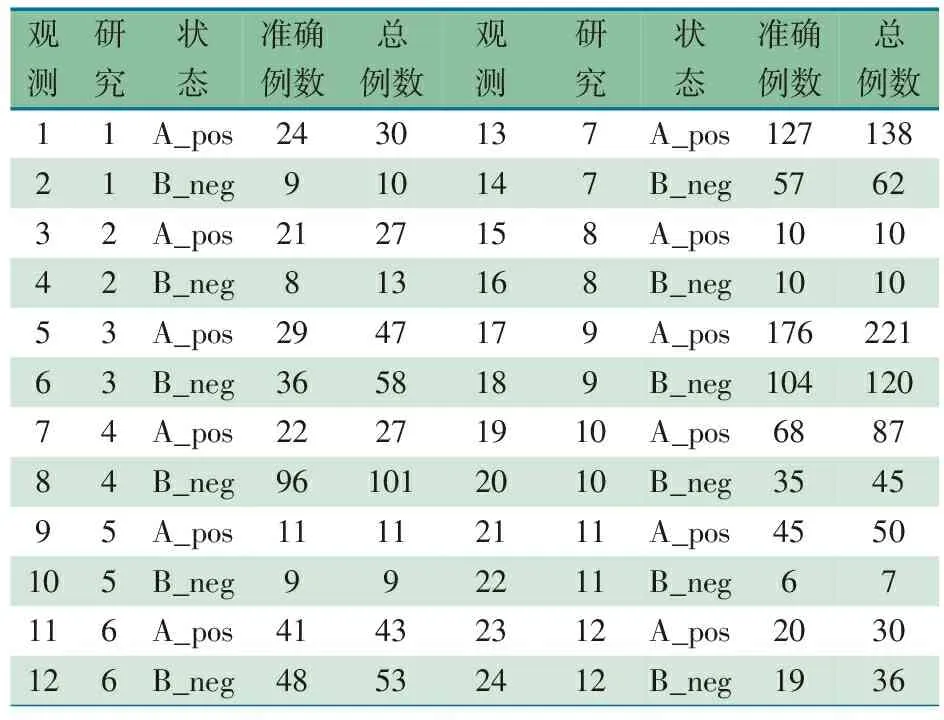
表2 待分析的双变量数据集

注 A_pos代表真阳性例数，B_neg代表真阴性例数

附录代码第1～4行调用PROC MCMC，其中包含有关采样和调整的代码选项(第2行)，也包含报告输出的选项(第3～4行)。丢弃的开动采样数量(nbi=100 000)被设定为MCMC采样(nmc=1000 000)的10%。MCMC采样间隔采用10来抽样以减少自相关。因此，后验分布由100 000个样本组成，对应于每百分位数1 000个样本。第6～8行3个ARRAY语句声明了模型变量，在“[]”括号提供了数组下标。“random eta”语句行声明指定了纳入分析的单个研究的双变量eta数组。双变量数组mu和协方差矩阵Sigma分别代表了公式2的BREM的5个参数。在第8行中，cov_uAB2实际上与cov_uAB是相同的。第10～11行PARMS语句将汇总估计“mu”和随机效应协方差矩阵“Sigma”声明为模型参数，第12～13行prior语句指定先验分布。在第12行中，无信息先验(noninformative prior)的均匀先验分布(uniform priors)被用于mu_A和mu_B，范围从-10到10。在灵敏度/特异度尺度上，对应于0.005%至99.995%的足够宽的参数范围。具有较大方差(例如100)的多变量正态先验也可以用于代替均匀先验。第13行将Wishart分布指定为随机效应协方差矩阵的多变量先验。

第9行的ARRAY语句定义了Wishart分布的同一性标度矩阵。第14～16行针对file_ bidata数据集的每个研究的特定数据记录进行评估。第17行实现公式1，第15～16行提供了灵敏度和特异度的对数转换，第14行实现了公式2的双变量模型。在第18～25行中，提供了进一步的模型计算结果，包括诊断比值比及其对数值、敏感度、特异度、阳性似然比、阴性似然比及其对数转换值等。第26～30行计算了与HSROC模型相关的5个参数。第32行调用内置绘图函数绘制Caterpillar图。

固定效应模型的SAS代码省略了与随机效应相关的所有代码(见附录代码2)。

运行程序时，每个受监控的模型参数都会生成一个MCMC样本链(Chain)，这通过第4行代码指定。这样的马尔可夫链(the Markov chains)是一个随机过程，其未来状态仅取决于当前状态，且独立于过去状态。作为稳健结果的先决条件，马尔可夫链应收敛到每个模型参数的独特后验分布。这可以通过程序的诊断代码(即第3行)进行评估。

2.3 评估链收敛 通过SAS PROC MCMC实现的马尔可夫链的收敛，可以采用踪迹图和自相关图来可视化评估，特别是通过评估链的混合性和平稳性。除了图形给出收敛性评估外，PROC MCMC同时给出不同收敛性诊断的统计值：蒙特卡罗标准误、自相关参数、Geweke诊断、Raftery-Lewis诊断、Heidelberger-Welch诊断、有效样本量等。需要注意的是，SAS PROC MCMC的所有收敛诊断都是使用默认参数执行的。显着性水平设定为P<0.05[10]。

3 结果

3.1 贝叶斯固定效应模型Meta分析结果 运行附录代码2后，可以获得贝叶斯固定效应模型Meta分析结果。包括主要统计结果部分和链收敛性评估部分。主要统计结果部分包含4个表格，分别为后验摘要表、后验可信区间表、后验相关系数矩阵和后验协方差矩阵。系统评价员主要关心后验摘要表和后验可信区间表。链收敛性评估部分包含7个表格和针对本(Highest posterior density，HPD)文待研究变量的自相关图。由于篇幅关系，这里仅提供后验摘要表和后验可信区间表的结果。后验可信区间表比较的是95%等尾(Equal-Tail)可信区间和95%最大后验密度可信区间的差异。资料见表3、表4。读者可以运行本文的附录代码，获取其他表格数据及自相关图。

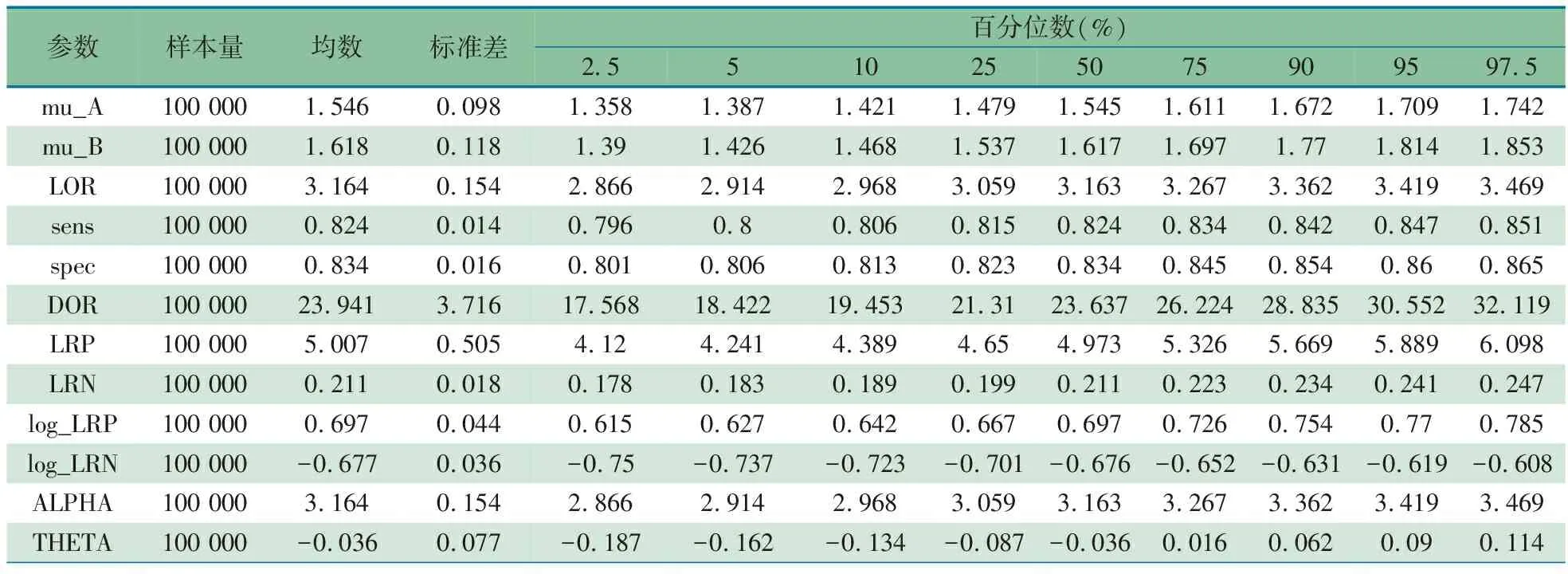
表3 固定效应模型后验摘要表

注 mu_A：敏感度的对数值，mu_B：特异度的对数值，LOR：诊断比值比的对数值，Sens：敏感度，spec：特异度，DOR：诊断比值比，LRP：阳性似然比，LRN：阴性似然比，log_LRP：LRP的对数值，log_LRN：LRN的对数值，ALPHA：HSROC模型α参数，THETA：HSROC模型θ参数

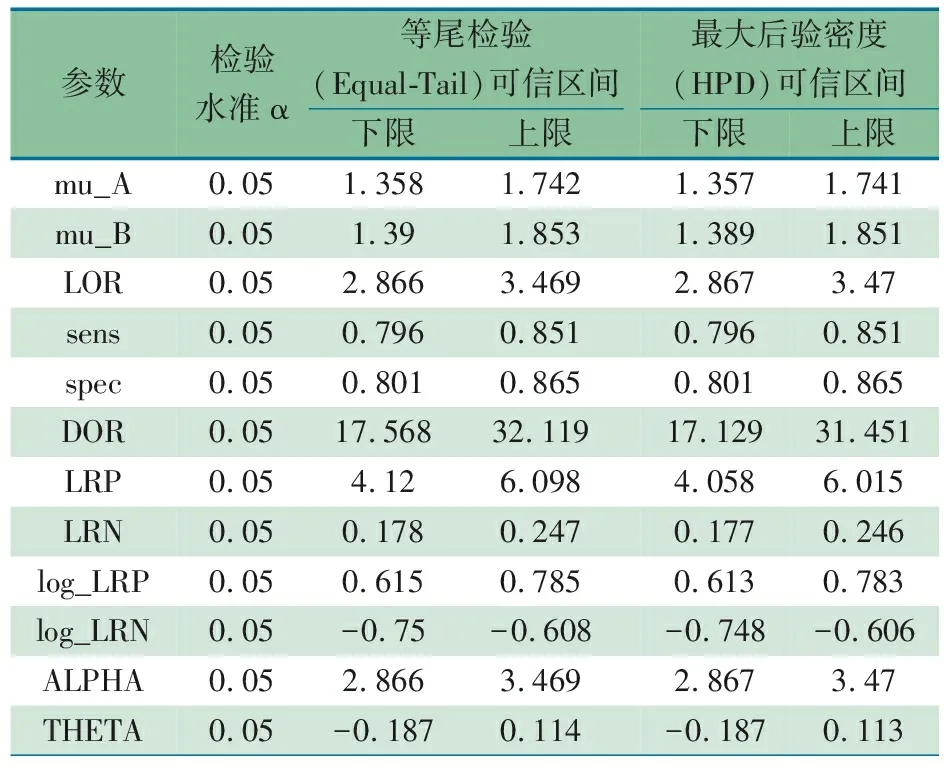
表4 固定效应模型后验可信区间表

注 mu_A：敏感度的对数值，mu_B：特异度的对数值，LOR：诊断比值比的对数值，Sens：敏感度，spec：特异度，DOR：诊断比值比，LRP：阳性似然比，LRN：阴性似然比，log_LRP：LRP的对数值，log_LRN：LRN的对数值，ALPHA：HSROC模型α参数，THETA：HSROC模型θ参数

表3、4数据显示，高分辨率超声诊断可复性盘前移位(ADDWR)的合并敏感度(Sen)为0.823(95%CI：0.796～0.851)，合并特异度(Spe)为0.834(95%CI：0.801～0.865)，诊断比值比(DOR)为23.94(95%CI：17.568～32.119)，阳性似然比(LRP)为5.007(95%CI：4.120～6.098)，阴性似然比(LRN)为0.2113(95%CI：0.178～0.247)；HSROC模型相关参数：α=3.164(95%CI：2.866～3.469)；θ=-0.036(95%CI：-0.187～0.114)。

3.2 贝叶斯随机效应模型Meta分析结果 运行附录代码3后，可以获得贝叶斯随机效应模型Meta分析结果。也包括主要统计结果部分和链收敛性评估部分(表5和6)。需要注意的是，表5和6没有提供单个试验的随机效应估计值。读者可以运行本文的附录代码，获取表5和6的单个试验的随机效应估计值、其他表格数据及自相关图。

表5和6数据显示，高分辨率超声诊断ADDWR的合并Sen 0.852(95%CI：0.766～0.924)，合并Spe 0.865(95%CI：0.760～0.944)，DOR 53.413(95%CI：11.855～170.4)，LRP 7.306(95%CI：3.325～15.946)，LRN 0.174(95%CI：0.083～0.296)；HSROC模型相关参数：α=3.739(95%CI：2.526～5.162)；θ=0.153(95%CI：-0.404～0.732)；BETA=0.233(95%CI：-0.384～0.866)；var_uAlpha=4.105(95%CI：1.171～11.813)；var_uTheta=0.134(95%CI：0.043～0.356)。

3.3 贝叶斯随机效应模型Meta分析的链收敛性评估结果 在本文的示例数据中，运行附录代码后，可以获得MCMC采样评估图，包括核密度图、踪迹图和自相关图。篇幅原因只提供了mu_A的结果(图1)。图1说明了针对SAS PROC MCMC参数mu_A的MCMC采样。在踪迹图中(图1A)，马尔可夫链很好地混合并通过遍历密度较低区域来探索其分布。在自相关图中(图1B)，在LAG=5的地方，mu_A的验后自相关是0.0296，因此很小。核密度图显示(图1C)，mu_A的后验分布类似于正态分布，其参数Mean=1.7850，标准差SD=0.3319。

3.4 贝叶斯随机效应模型Meta分析的Caterpillar森林图 SAS PROC MCMC可以调用内置宏命令“%CATER”来绘制森林图。本文示例数据绘制的森林图见图2。

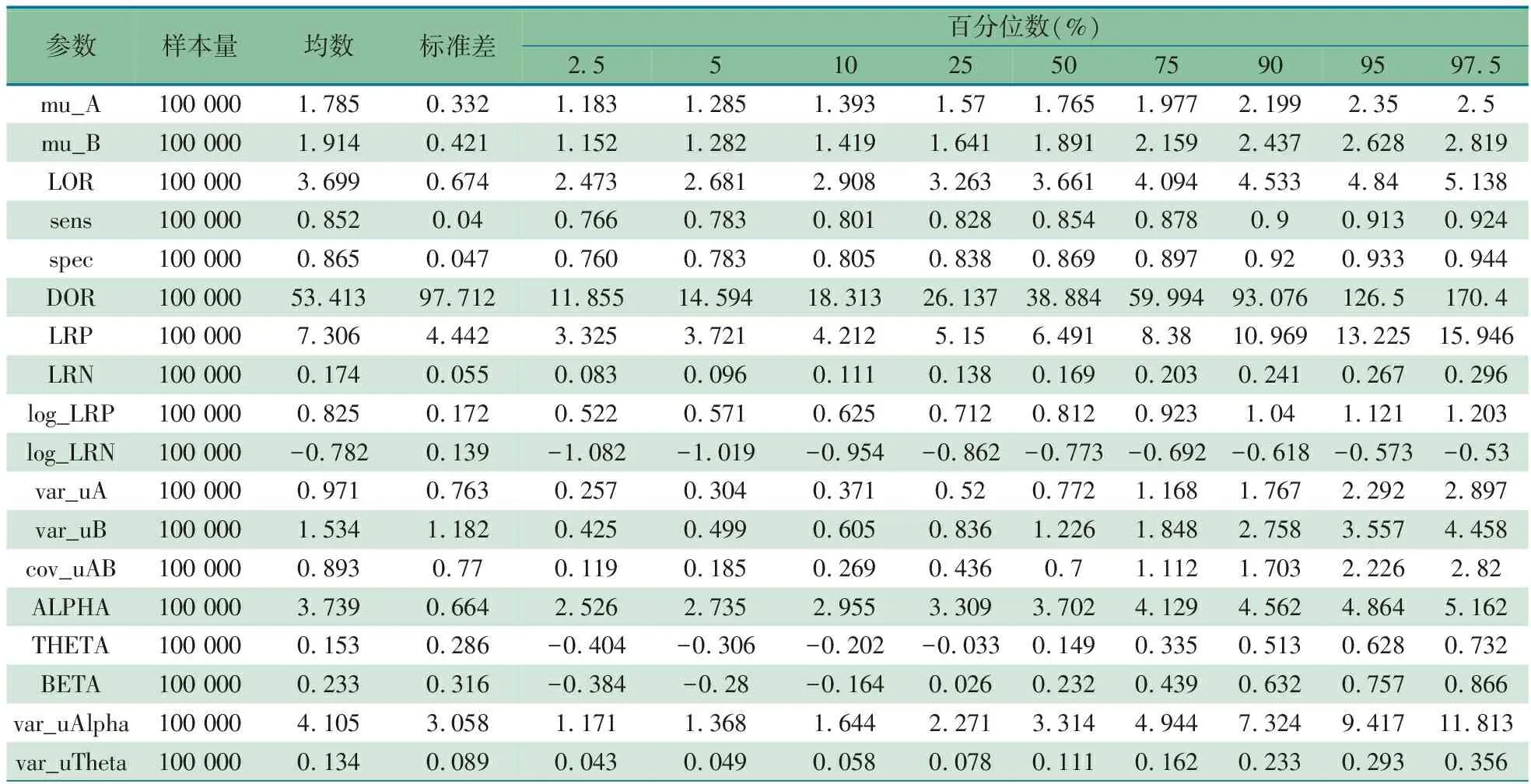
表5 随机效应模型后验摘要表

注 mu_A：敏感度的对数值，mu_B：特异度的对数值，LOR：诊断比值比的对数值，Sens：敏感度，spec：特异度，DOR：诊断比值比，LRP：阳性似然比，LRN：阴性似然比，log_LRP：LRP的对数值，log_LRN：LRN的对数值，ALPHA：HSROC模型α参数，THETA：HSROC模型θ参数

表6 随机效应模型后验可信区间表

4 讨论

SAS 软件使用广泛，其强大的编程思维可以灵活地处理各种数据。相对于经典的统计推论方法，贝叶斯方法长短处兼有[14]。随着计算方法的进步，贝叶斯推论方法的发展加快。在SAS9.2版本之前，SAS无法实现贝叶斯模型分析。贝叶斯分析模型在SAS软件里对口的过程是PROC MCMC，作为试验版本迄始于SAS 9.2，在SAS 9.3中有所增强，并提供了对应于随机效应模型的Random Statement等。本文介绍了通过SAS 9.4版本的PROC MCMC 过程、随机效应模型来实现诊断性试验的贝叶斯Meta 分析。

基于特异度和灵敏度的BREM目前是最受推荐的诊断准确性荟萃分析模型[6, 15, 16]。通过BREM的随机效应，研究人员可以获得未知的灵敏度和特异度的真实差异。这种真实差异已被证明在原始研究之间是存在的。此外，该模型认为这些敏感度和特异度的随机效应可能是相关的。Harbord等已经证明BREM在数学上等同于HSROC模型[4]。本文SAS代码获取HSROC参数，便是直接从双变量的结果获得。

在SAS软件中，可以通过不同的过程步实现灵敏度和特异度的BREM，包括SASPROC GLIMMIX和SAS PROC MIXED等[3,17]。在SAS PROC GLIMMIX中，公式2的广义线性混合模型由最大似然拟合，其中边际分布在迭代中以数值方式近似，直到满足收敛准则。 SAS PROC GLIMMIX假定其模型参数的预定义固定分布，并且计算速度非常快。van Houwelingen等介绍了SAS PROC MIXED实现双变量随机效应模型的原理，并提供了相关的SAS代码[17]。

图1 MCMC采样分析图(变量=mu_A)

图2 各个研究的汇总Caterpillar森林图

与SAS PROC GLIMMIX和SAS PROC MIXED相比，贝叶斯SAS PROC MCMC通过数值模拟获得其结果，而不是通过分析或迭代近似获得其结果。但需要更多的计算时间。由此产生的后验分布取决于先验和数据，不需要正态分布。贝叶斯分析可以直接估计参数的任何函数。例如，合并的阳性似然比和阴性似然比及其95%可信区间均可以从合并的灵敏度和特异度估计，同理，可以获得阳性验后概率和阴性验后概率。

SAS PROC MCMC实现了马尔可夫链蒙特卡罗(MCMC)方法，该方法结合了蒙特卡罗积分和马尔可夫链采样。蒙特卡罗积分是一种数值积分方法，通过采用离散样本简化连续分布。样本量较大时，样本的直方图近似于连续分布，可以通过样本进行有关分布的任何推断，例如估计平均值和95%可信区间，提供了一种从目标密度中提取样本的方法。马尔可夫链是一个随机过程，其未来状态仅依赖于当前状态并且与过去无关。这种属性允许马尔可夫链简化复杂问题，因为链中的下一个样本仅取决于前一个样本[18]。马尔可夫链需要一个在目标分布范围内的初始值。样本通过SAS PROC MCMC中的随机漫步Metropolis算法和WinBUGS中的Gibbs采样获得[19]。

应用MCMC方法，需要评估Markov链的收敛诊断，而这种收敛诊断可以帮助解决两个问题。首先，明确马尔可夫链是否变得平稳(最初的非平稳样本被丢弃为“退火(Burn-in)”)。其次，明确后验分布需要多少样本。理论上，样本越大，越容易准确地估计模型参数，但计算时间会成比例增加。正常情况下，计算时间是限制MCMC样本的主要原因。

本文提供的代码程序是在Menke提供的SAS 软件进行贝叶斯诊断性试验Meta 分析的PROC MCMC 过程代码上修改的。在Menke的文章中，作者针对敏感度和特异度的贝叶斯双变量随机效应荟萃分析，提出了统计模型及其在SAS PROC MCMC的实施过程。提供的程序代码在50个Meta分析中进行了实证评估，结果与相应的WinBUGS方法非常相似[9; 10]。本文在Menke提供的代码上进行实例应用，并对代码做了简单修改，可以直接获得诊断比值比、阳性似然比及阴性似然比，读者可以比较两种代码的异同。鉴于学术性，读者在学习本文提供的代码时，请务必参考学习Menke的原文，并引用原文作为参考文献[10]。

在本文引用的示例数据中，董小宇等利用STATA实现了HSROC模型的Meta分析[12]，这给本文的SAS代码学习提供了便利的实证基础。通过对比发现，董小宇等的研究结果中，高分辨率超声诊断ADDWR的Sen=0.84(95%CI：0.76～0.90)，Spe=0.87(95%CI：0.77～0.93)，而本文Sen为0.852(95%CI：0.766～0.924)，Spe为0.865(95%CI：0.760～0.944)； 两者统计结果极其接近，证明SAS PROC MCMC是可以实现HSROC模型计算的。需要注意的是，在贝叶斯统计理论中，参数θ是一个随机变量，结合样本信息和先验信息可以构造一个区间，这个区间称之为可信区间(Credit interval)，这个应该区别于经典统计学派的置信区间(Confidence interval)。贝叶斯理论可以简单描述为“有95%的概率使得参数θ落在可信区间内”。董小宇等的文章提供的“CI”属于经典统计学的“置信区间”，在统计学概念上，略有不同。

5 结论

鉴于SAS软件强大的编程能力，贝叶斯SAS PROC MCMC可以非常方便地实现基于敏感度和特异度的BREM的诊断性试验的Meta分析。

/* 附录代码1 建立数据集*/

ods html file='Data.html' style=statistical;

DATAfile_data;

length author $20;

input study author $ year tru_pos fal_pos fal_neg tru_neg;

ref_pos = tru_pos + fal_neg;

ref_neg = tru_neg + fal_pos;

datalines;

1 Yangjieping 2012 24 1 6 9

……

;run;

PROCPRINTdata=file_data;run;

DATAfile_bidata; set file_data;

status='A_pos'; true=tru_pos; total=ref_pos; output;

status='B_neg'; true=tru_neg; total=ref_neg; output;

keep study status true total;run;

PROCPRINTdata=file_bidata;run;

/* 附录代码2 固定效应模型*/

ods html file='Fixed-effects_model.html' style=statistical;

ods graphics on;

PROCMCMCdata=file_bidata outpost=file_postout_fixed propcov=quanew

nbi=100000nmc=1000000ntu=1000thin=10seed=1simreport=100

diagnostics=all stats(percentage=(2.5510255075909597.5))=all

monitor=(mu_A mu_B LOR sens spec DOR LRP LRN log_LRP log_LRN ALPHA THETA) dic;

title 'Bayesian bivariate fixed-effects model';

/*变量声明和初始化 */

array mu[2] mu_A mu_B; /*合并敏感度和特异度的Logit转换*/

parms mu:0;

prior mu: ～ unif(-10,10);/*对每个数据记录评估以下指令*/

if status='A_pos' then p = logistic(mu_A);

if status='B_neg' then p = logistic(mu_B);

model true ～ binomial(total, p);

/*计算其他双变量参数*/

LOR = mu_A + mu_B; /*诊断比值比的对数值*/

sens = logistic(mu_A); /*合并敏感度*/

spec = logistic(mu_B); /*合并特异度*/

DOR=(sens/(1-spec))/((1-sens)/spec);

LRP = sens/(1-spec); /*阳性似然比*/

LRN = (1-sens)/spec; /*阴性似然比*/

log_LRP = log10(sens/(1-spec)); /*阳性似然比的log10转换*/

log_LRN = log10((1-sens)/spec); /*阴性似然比的log10转换*/

/*计算HSROC参数*/

THETA = (mu_A - mu_B)/2;

ALPHA = (mu_A + mu_B);

run;

/*附录代码3 随机效应模型*/

ods html file='Random-effects_model.html' style=statistical;

ods graphics on;

#1PROCMCMCdata=file_bidata outpost=file_postout_random propcov=quanew

#2nbi=100000nmc=1000000ntu=1000thin=10seed=1simreport=100

#3diagnostics=all stats(percentage=(2.5510255075909597.5))=all

#4monitor=(mu_A mu_B LOR sens spec DOR LRP LRN log_LRP log_LRN var_uA var_uB cov_uAB ALPHA THETA BETA var_uAlpha var_uTheta) dic;

#5title 'Bayesian bivariate random-effects model';

#6array eta[2] eta_A eta_B; /*纳入研究特定的随机效应*/

#7array mu[2] mu_A mu_B;

#8array Sigma[2,2] var_uA cov_uAB cov_uAB2 var_uB;

#9array S[2,2] (1001);

#10parms mu:0;

#11parms Sigma {0.01000.01};

#12prior mu: ～ unif(-10,10);

#13prior Sigma ～ iwish(2, S);

#14random eta ～ mvn(mu, Sigma) subject=study monitor=(eta_A eta_B);

#15if status='A_pos' then p = logistic(eta_A);

#16if status='B_neg' then p = logistic(eta_B);

#17model true ～ binomial(total, p);

/*计算其他双变量参数*/

#18LOR = mu_A + mu_B; /*诊断比值比的对数值*/

#19sens = logistic(mu_A); /*合并敏感度*/

#20spec = logistic(mu_B); /*合并特异度*/

#21DOR=(sens/(1-spec))/((1-sens)/spec);

#22LRP = sens/(1-spec); /*阳性似然比*/

#23LRN = (1-sens)/spec; /*阴性似然比*/

#24log_LRP = log10(sens/(1-spec)); /*阳性似然比的log10转换*/

#25log_LRN = log10((1-sens)/spec); /*阴性似然比的log10转换*/

/*计算HSROC参数*/

#26THETA = (mu_A*(var_uB/var_uA)**0.25- mu_B*(var_uA/var_uB)**0.25)/2;

#27ALPHA = (mu_A*(var_uB/var_uA)**0.25+ mu_B*(var_uA/var_uB)**0.25);

#28BETA = log(sqrt(var_uB/var_uA));

#29var_uTheta = (sqrt(var_uA*var_uB) - cov_uAB)/2;

#30var_uAlpha = (sqrt(var_uA*var_uB) + cov_uAB)*2;

#31run;

#32%CATER(data=file_postout_random, var=eta:);