基于改进的蚁群算法的测试数据自动生成方法

2019-08-23苗晓旭胡玉露徐豪曾佩杰

电子技术与软件工程 2019年13期

文/苗晓旭胡玉露徐豪曾佩杰

1 引言

随着软件规模的逐渐增大和软件复杂度的不断提升，传统手工编写测试数据的方法已不再适用。高效可行的测试数据自动生成方法不仅能保证测试覆盖率，还可以较大程度降低测试成本，对自动化的软件测试来说意义重大。

目前，测试数据自动生成方法主要有动态、静态和智能优化三类方法。动态法有迭代松弛法、试探法、程序插桩法等；静态法有符号执行法、随机法；智能优化算法有禁忌搜索算法、蚁群算法、遗传算法等。

蚁群算法的搜索过程采用分布式计算方式，相较其它智能算法具有较高的计算能力和运行效率，但算法的搜索精度仍有待完善。因此本文提出改进的蚁群算法，在传统蚁群算法的基础上引入相似度影响因子，能够增加算法的全局搜索能力。并将改进的蚁群算法应用到测试数据自动生成问题中。

2 测试数据自动生成模型

设待测路径为P，采用改进的蚁群算法自动生成的输入参数变量为X={x1，x2，…，xn}，输入参数变量X的实际执行路径为P’，当P’=P时，所取的X则为最优测试数据。

测试数据自动生成模型主要包括以下三个基本模块：

（1）程序分析模块：静态分析被测程序的语义、语法和词法，生成测试路径总集。从总集中任选一条逻辑路径并以此为基础插桩生成插桩程序。最后分析并确认输入变量集合。

（2）算法解算模块：根据输入变量集合，对变量编码组合生成初始蚁群；根据被测插桩程序的运行结果反复进行编码的迭代更新，直到找到最优解或达到最大迭代次数。

（3）驱动程序模块：获取输入的测试数据变量，调用并运行桩程序，对每个测试数据完成评价后反馈给算法解算模块。如图1所示。

3 改进的蚁群算法设计

3.1 蚁群算法

蚁群算法是一种仿生优化算法，模拟了蚂蚁在运输食物过程中搜索选择食物源到蚁穴的最短运输路线的过程。通过追寻具有大浓度信息素的路线舍弃具有低浓度信息素的路线，同时在运输过程中受到自身信息素释放及信息素挥发的影响，蚁群不断修正运输路线，最终找到一条信息素浓度最大也是距离最短的运输路线。从仿生模拟过程可以看出来，蚁群算法是具备进化能力的随机搜索算法，通过对备选解集合的不断迭代优选来寻求最优解。迭代优选过程主要包括两个阶段：适应阶段和协同阶段。在适应阶段，各备选解利用积累的数据不断调整自身模态；在协同阶段，各备选解之间通过数据交换，最终共同向更优的解逼近。

3.2 改进的蚁群算法

算法为了表示最优路径和实际行走路径之间的互信息熵，在蚁群算法的概率算子中增加了一个相似度影响因子：

其中：

i:待测路径上的节点

j:最优路径上的节点

Ii，j:为i与j之间的互信息

p(i，j):为i节点和j节点的联合概率分布

p(i):i节点的边缘概率分布

p(j):j节点的边缘概率分布

本方法使用联合直方图法对互信息进行计算。

最优路径的存在会对蚁群的搜索方向起到引导作用，而互信息则为主要的引导元素，蚁群会偏向于选择与当前状态互信息最大的节点作为下一个目标。同时，将该影响因子引入蚁群算法，路径选择概率函数改写为：

其中：

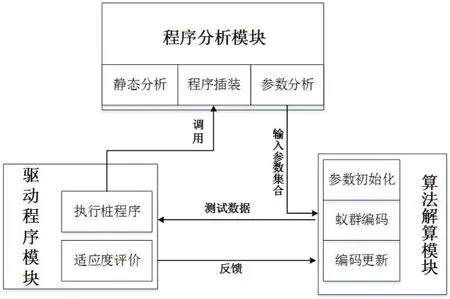
图1：测试数据自动生成模型

图2：直角三角形最优个体迭代次数算法比对

[γi，j(t)]α:在t时刻散布在第i个节点和第j个节点间的互信息

di，j:节点i与节点j之间的距离

allow(i):当蚁群位于第i个节点时未访问的节点集

α:信息素的关重度

β:可见性的关重度

θ:互信息的关重度

设满足式（2）的蚁群称为A类蚁群，该蚁群会因优先选择互信息量最大的节点导致自身极易易陷入局部最优节点。为了解决陷入局部最优的问题，引入B类蚁群，其γ为A类蚁群的相反数，从而使该蚁群有一定的能力修正局部最优点。

综上所述，本文改进的蚁群算法步骤如下：

Step1:对参数变量进行初始化；

Step2:使用传统蚁群算法，蚁群数为m0，迭代次数为n0；

Step3:根据传统蚁群算法得到的结果，对联合直方图矩阵HBT进行初始化；

Step4:把蚁群分为三类，一类为传统蚁群，另两类分别为A类蚁群和B类蚁群，蚁群数量分别为m1、m2和m3；

Step5:对三类蚁群的主要参数进行初始化；

Step6:第一类蚁群利用传统蚁群算法进行计算，之后记录下其互信息并存储行进路径；

Step7:A类和B类蚁群则利用公式（2）进行计算，之后分别记录下其互信息并存储行进路径；

Step8:根据步骤Step6～Step7得到的所有蚁群的路径集合对联合直方图矩阵HBT进行更新；

Step9:判断计算结果是否收敛或达到最大迭代次数，否则转到Step5；

Step10:输出最优路径即最优解。

4 实验验证与分析

本文采用三角形判别问题对算法进行可行性验证，选取逻辑较复杂且更具代表性的直角三角形判别问题生成测试数据，并把计算结果与传统蚁群算法进行了对比。

实验设置三角形的3条边L1、L2、L3，每个参数占8位，取值范围为[0，255]，长度为24。例如，三角形L1=6，L2=8，L3=10，则编码表示为（00000110 0000100000001010）。实验随机选取15-90个蚂蚁数作为初始蚁群，设定三类蚁群数m1=m2=m3，信息素的关重度α为1.5，可见性关重度β为5，互信息关重度θ为2，信息挥发因子为0.5，信息素强度为100，最大迭代次数n0为1000。

实验开始，输入被测程序并进行静态分析，根据分析结果对选定的路径进行插桩。对直角三角形参数进行初始化，分别执行传统蚁群算法和改进蚁群算法。调用插装程序获得评价值，引导蚁群更新，得到最优测试数据。两种算法分别运行10次，记录蚁群规模为15、30、45、60、75、90时的平均迭代次数，见图2。

实验结果表明：

（1）在其他参数变量均相同的情况下，随着蚁群规模的逐步增大，本文改进蚁群算法和传统蚁群算法生成最优测试数据的平均迭代次数会逐步减小；

（2）在基本参数设置均相同的情况下，对于特定情况的最优测试数据生成，本文改进蚁群算法明显少于传统蚁群算法的平均迭代次数；

（3）传统蚁群算法在运行过程中出现了陷入局部最优的情况，改进蚁群算法有效地弥补了局部最优的缺陷，减小了搜索停滞不前的可能性。

改进的蚁群算法相较传统蚁群算法，能够更快速、精确地找到测试数据的可行解。因此，改进的蚁群算法可以使测试数据自动生成过程更加高效。