结合变压器正反激原理的动力电池主动均衡方法

李玉,徐俊,彭程,梅雪松

(1.西安交通大学陕西省智能机器人重点实验室,710049,西安; 2.西安交通大学机械制造与系统工程国家重点实验室,710049,西安; 3.西安交通大学机械工程学院,710049,西安)

随着电动汽车的快速发展,锂离子电池因具有自放电率低、电压水平高、充电效率高、能量密度高、没有记忆效应等优点而被广泛应用[1-2]。为了达到电动汽车所需要的输出电压和续驶里程,需要将许多单体电池串并联连接构成电池组[3-5]。然而,由于制造和使用环境的差异,电池组中的电池状态存在不一致现象,导致电池组容量下降,甚至出现起火、爆炸等危险[6-7]。电池均衡是目前解决电池不一致问题的有效方法[8]。

常见的电池均衡方法有被动均衡和主动均衡[9-10]:被动均衡方法主要采用耗散元件将电池多余的能量以热能的形式耗散,结构简单,但能量损耗严重,均衡效率较低,热管理难度大[11];主动均衡方法因可以有效提高均衡速度和效率而被广泛研究。根据能量转移器件的不同,主动均衡可以分为基于电感、电容、变压器等均衡方法[12]。基于电感的均衡方法只能在相邻电池单体间实现能量的直接转移,在不相邻电池间均衡时,能量需经多次中间转换,均衡效率和速度大大降低[13-14];基于电容的均衡方法受限于均衡电池间的电压差,电压差较小时,均衡能力较差,甚至无法均衡[15-16];基于变压器的均衡方法分为反激和正激的均衡方法[17-20],其中基于变压器反激原理的均衡方法,由于每节单体电池需要变压器及控制信号,元器件和控制信号数量较多,因此系统成本高[17],基于变压器正激原理的均衡方法,由于增加了额外的去磁电路,因而使得结构体积大、成本高[18]。

电动汽车电池均衡系统要求均衡电路具有较少的元器件数量、简单的控制复杂度、较快的均衡速度、低的系统成本,而上述的均衡方法或多或少存在一些问题,因此本文基于传统变压器均衡方法提出了一种结合变压器正反激原理的电池单元与电池组间均衡方法。该方法将变压器正激与反激原理相结合,同一电池单元内的电池采用变压器正激原理实现均衡,电池单元与电池组间采用变压器反激原理实现均衡。首先,设计了一种均衡电路的拓扑结构,分别分析了在两种工作模式下的均衡原理和实现条件。并设计了相应的均衡控制策略,在不同条件下选择对应的均衡模式。然后,搭建电池均衡实验平台,验证所提出的均衡方法和控制策略的可行性和有效性。实验结果表明,结合变压器正反激原理的电池均衡方法能够在使用较少的元器件、无需去磁电路、结构成本低的情况下达到良好的均衡效果。

1 均衡电路设计

(a)整体均衡结构

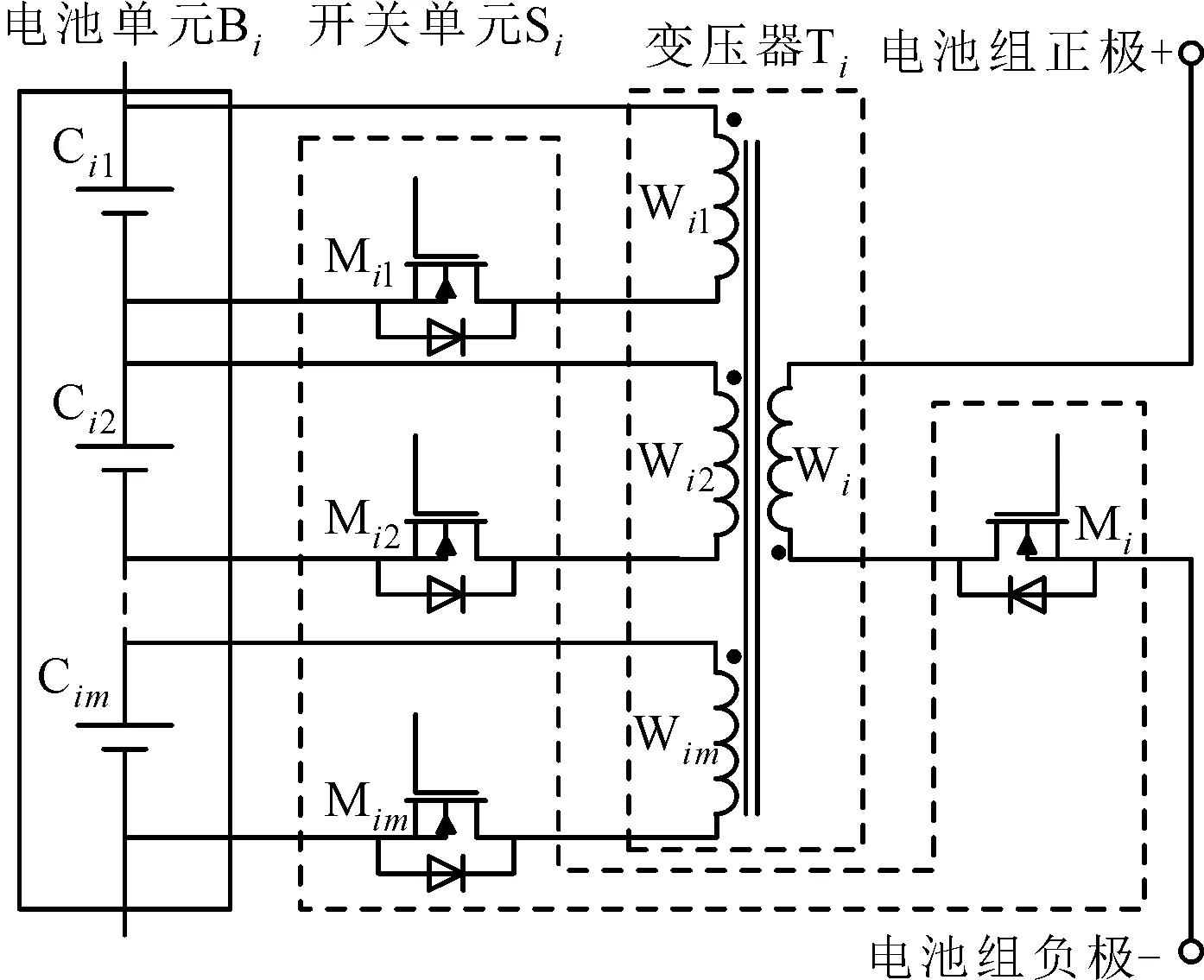
(b)第i个模组均衡结构图1 均衡拓扑结构

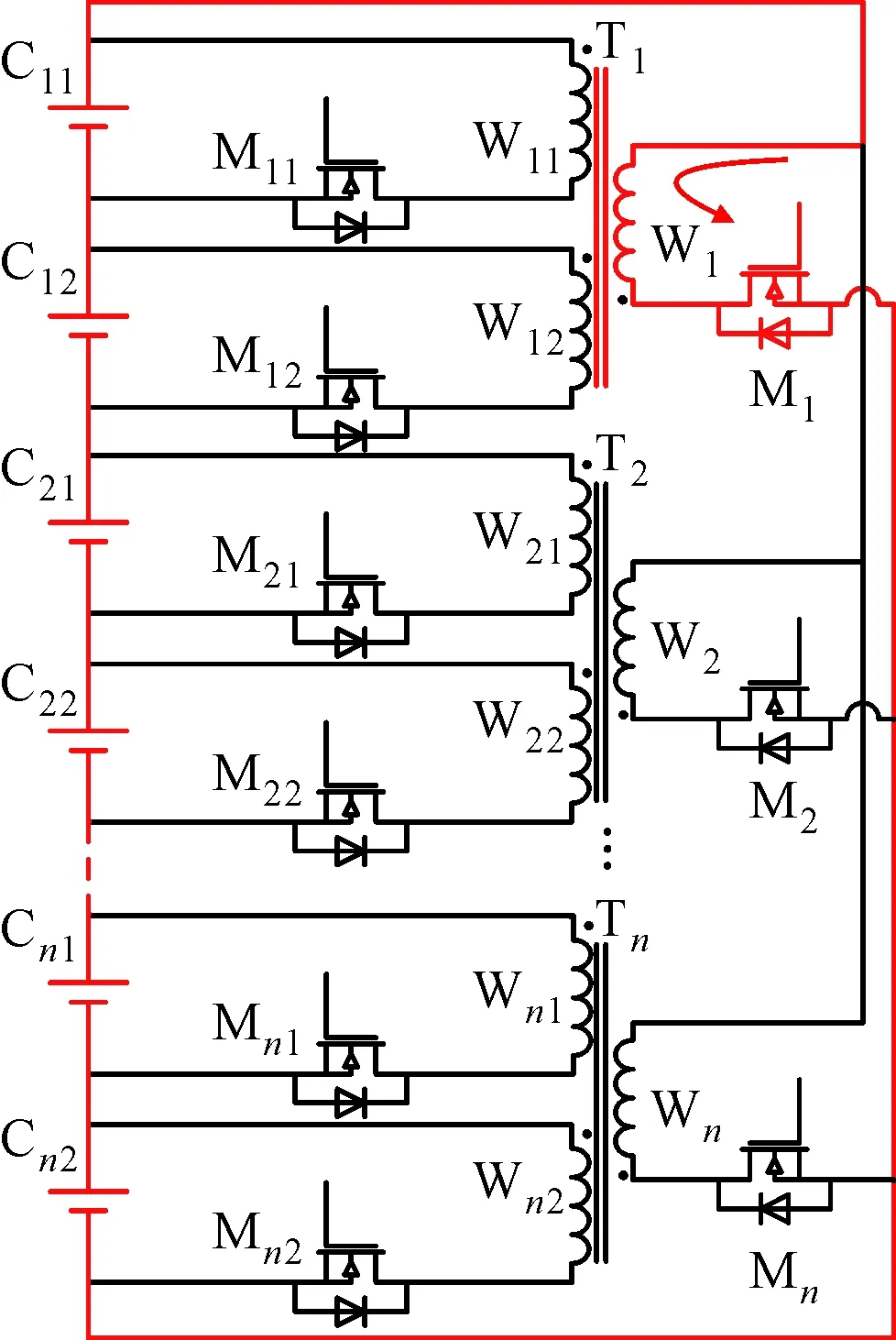
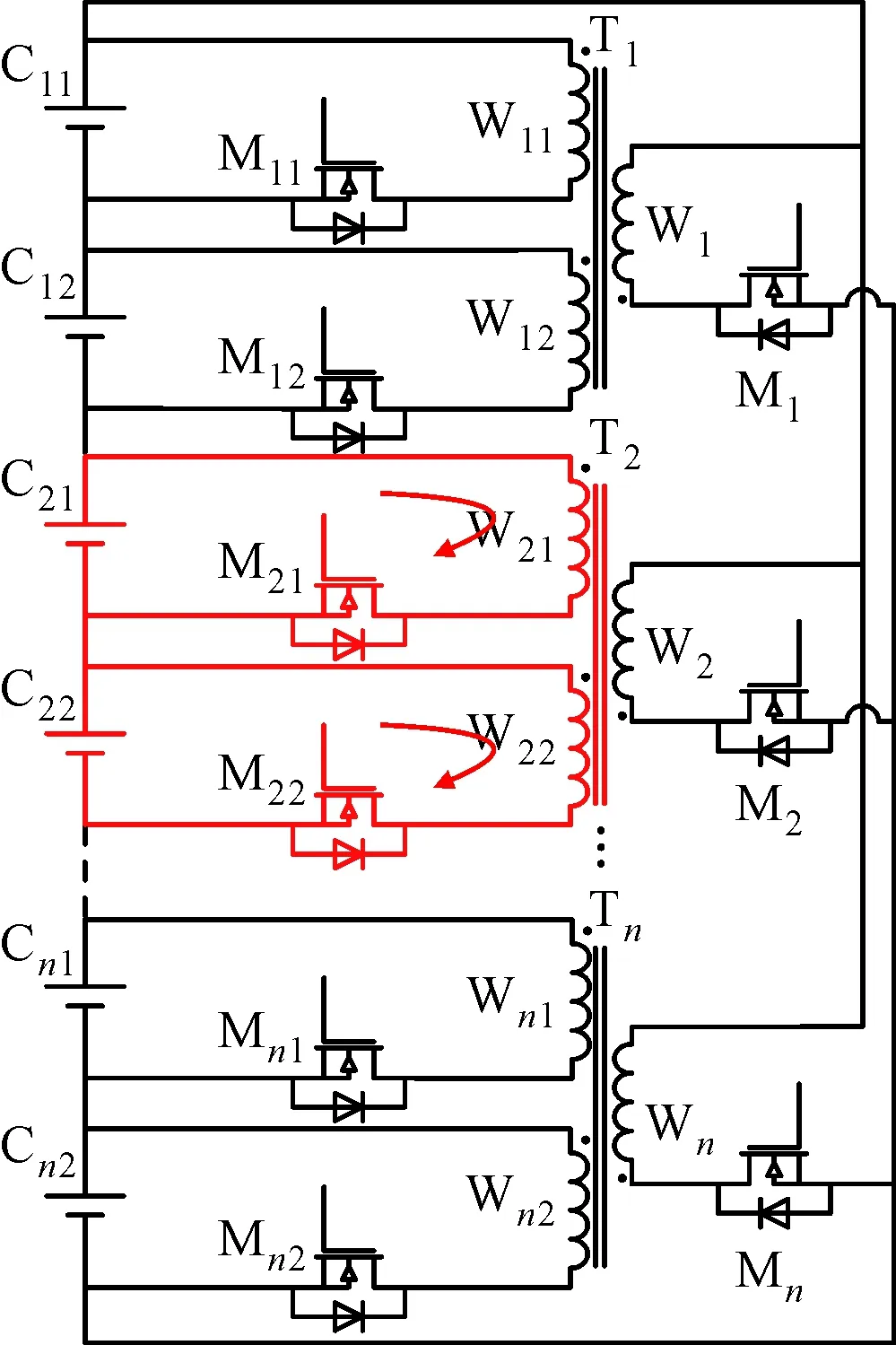
电池均衡方法是利用适当的均衡电路拓扑结构,使能量在电池间或电池与电池组间转移,从而消除电池间的差异,保证电池组中各单体电池处于均衡状态。本文提出的结合变压器正反激原理的主动均衡方法,可以同时实现电池间和电池与电池组间的均衡。整体均衡结构如图1a所示,均衡系统分为n个均衡模组,每个模组中包含电池单元、开关单元和变压器。以第i个模组为例,均衡结构如图1b所示,电池单元Bi由m个相邻的电池Cij(j=1,2,…,m)组成;开关单元Si由电池组对应的MOS管Mi和电池对应的m个MOS管Mij(j=1,2,…,m)构成;变压器Ti有m+1个绕组,一次侧对应绕组Wi,其两端分别与电池组正负极相连,二次侧的m个绕组Wij(j=1,2,…,m)分别连接电池单元中m节电池。

如图1所设计的结合变压器正反激的主动均衡结构,均衡系统实现模组化,同一模组内的电池共用变压器,均衡元器件数量明显减少;在均衡过程中,电池单元内由于变压器正激均衡产生的剩余磁能是由电池单元与电池组间的反激变压器消除,不需要额外的消磁电路,均衡元器件数量进一步减少;一个均衡模组只需一对互补的PWM信号分别控制电池组和均衡模组内电池对应的MOS管,大大降低了MOS管驱动电路的控制信号数量和控制复杂度;各模块互不影响,可以同时独立实施均衡,能量可以在电池组与电池单元间实现双向流动,使得均衡电路具有较快的均衡速度,使用成本降低;利用变压器反激原理实现电池组与电池单元间能量转移的同时,电池单元内的电池利用变压器正激原理实现均衡,变压器的磁芯充分利用,功率密度较高。

2 均衡电路工作原理

根据本文所提出的一种结合变压器正反激原理的主动均衡电路,每个均衡模组只需要一对互补的PWM信号控制相应的MOS管,即PWM+和PWM-。其中,PWM-控制信号是为了防止由MOS管体二极管压降造成能量损失。根据能量转移方向的不同,均衡系统分为两种工作模式:电池组向电池单元充电以及电池单元向电池组放电。

为了简化均衡原理的分析过程,做以下假设:

(1)每个均衡模组的电池单元中包含两个串联的电池单体,即模组中m=2;

(2)电池单元与电池组电压关系如下

(1)

式中:Vave,1和Vave,2分别为电池单元1和电池单元2的平均电压;Vave,p为电池组平均电压。

2.1 电池组向电池单元充电

对于电池组向电池单元充电的均衡模式,均衡过程分为3个阶段。第1阶段,电荷从电池组转移至变压器一次侧绕组;第2阶段,变压器将储存的电荷转移至电池单元;第3阶段,将所有MOS管关断以保证电路运行在断续模式(DCM)。以电池组向电池单元1转移电荷为例,均衡过程中的关键波形如图2所示。

第1阶段(t0-t1):如图2a所示,在t0时刻,MOS管M1导通,电池组与M1、变压器T1的一次侧绕组W1形成闭合回路。电荷从电池组转移至绕组W1,电流变化如图3a所示。为了计算简便,忽略电流环路中的内阻。

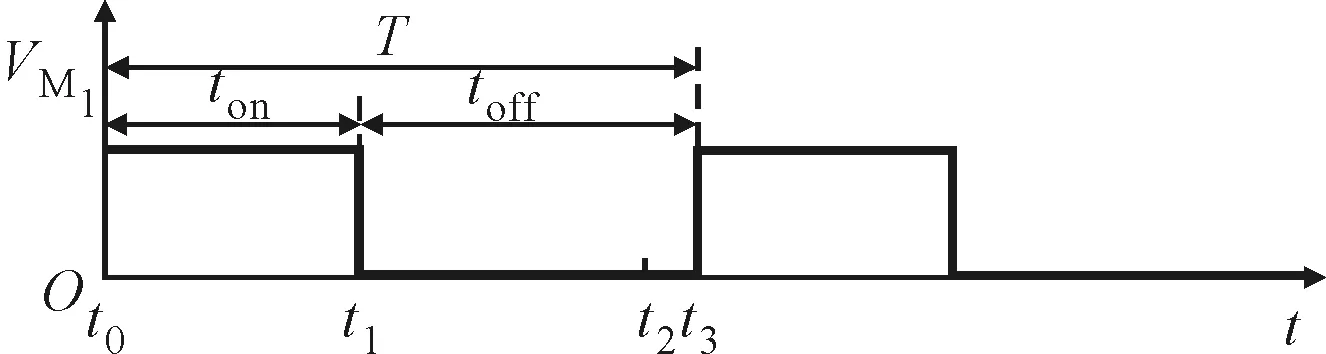
(a)MOS管M1上的电压波形

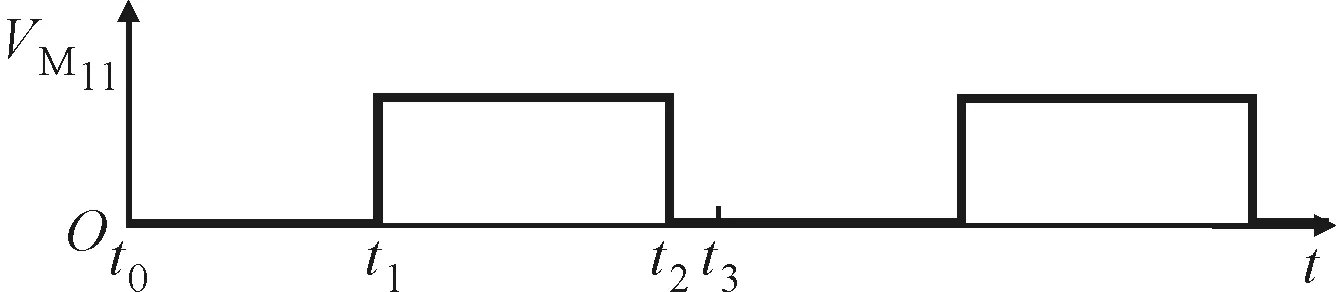
(b)MOS管M11上的电压波形

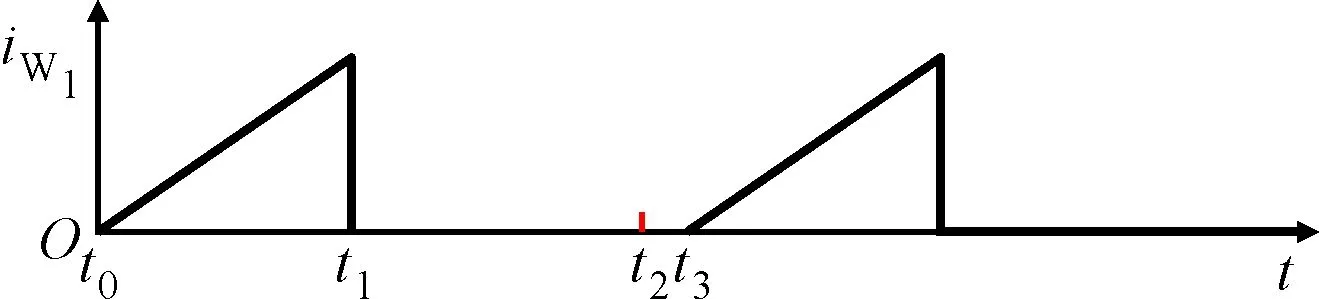
(c)变压器T1一次侧绕组W1上的电流波形

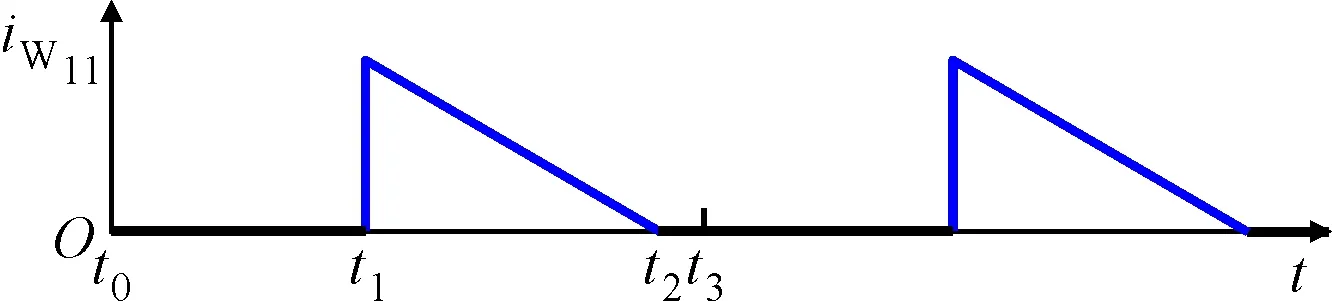
(d)变压器T1二次侧绕组W11上的电流波形

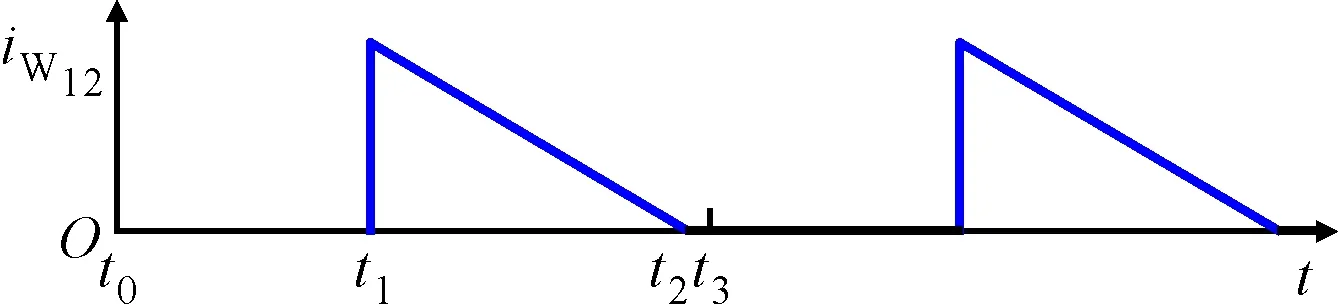
(e)变压器T1二次侧绕组W12上的电流波形图2 电池组向电池单元充电关键波形

根据基尔霍夫电压定律,通过一次侧绕组W1的电流iW1与其两端电压VW1的关系如下

(2)

式中:L1为变压器T1一次侧绕组W1的电感值。

由于变压器工作在DCM下,初始电流iW1,t0=0,解一阶微分方程式(2)可得流经绕组W1的电流

(3)

M1导通时,绕组线圈W1两端的电压值VW1近似等于电池组端电压

VpVW1=Vp

(4)

因此,如图2c所示,当t=t1时,电流达到最大值,峰值电流IW1,peak为

(5)

第2阶段(t1-t2):如图2b所示,在t1时刻,M1关断的同时,M11和M12导通。电池单体C11与M11、变压器T1的二次侧绕组W11形成闭合回路;电池单体C12与M12、二次侧绕组W12形成闭合回路。电荷从变压器转移至电池单元,电流变化如图3b所示。

根据安培环路定则,可得

N11iW11,t1+N12iW12,t1=N1iW1,t1=N1IW1,peak

(6)

式中:N11和N12分别为绕组W11和W12的匝数;N1为绕组W1的匝数;iW11和iW12分别为通过绕组W11和W12的电流。

由于各电池均衡结构对称,因此,变压器二次侧绕组匝数和电感值均相同,令

N11=N12=N10

(7)

L11=L12=L10

(8)

结合式(6)(7)可得

(9)

根据基尔霍夫电压定律,可得如下关系

(10)

(11)

式中:VW11和VW12分别为绕组W11和W12端电压。

流经绕组W11和W12的电流波形如图2d和图2e所示,电池C11和C12的充电电流可表示为

(12)

(13)

如式(12)和(13)所示,电池充电电流与其端电压成反比,因此,具有越低电压的电池,其充电电流越大,满足均衡结构设计要求。

第3阶段(t2-t3):在此阶段,关闭均衡电路中的所有MOS管,确保变压器工作在DCM中。

2.2 电池单元向电池组放电

对于电池单元向电池组放电的均衡模式,电荷转移方向与前一模式相反。以电池单元2向电池组转移电荷为例,关键波形如图4所示,均衡过程同样可分为3个阶段。

第1阶段(t0-t1):如图4a所示,M21和M22同时导通,电荷从电池C21和C22分别转移至变压器T2的二次侧绕组W21和W22,电流流动如图5a所示。

流经绕组W21和W22的电流波形如图2c和图2d所示,根据基尔霍夫电压定律,流过绕组W21和W22的电流iW21和iW22分别可表示为

(14)

式中:L11为变压器T2二次侧绕组W21的电感值。

(15)

式中:L12为变压器T2二次侧绕组W22的电感值。

由于变压器结构对称,二次侧绕组电感值相同,令

L21=L22=L20

(16)

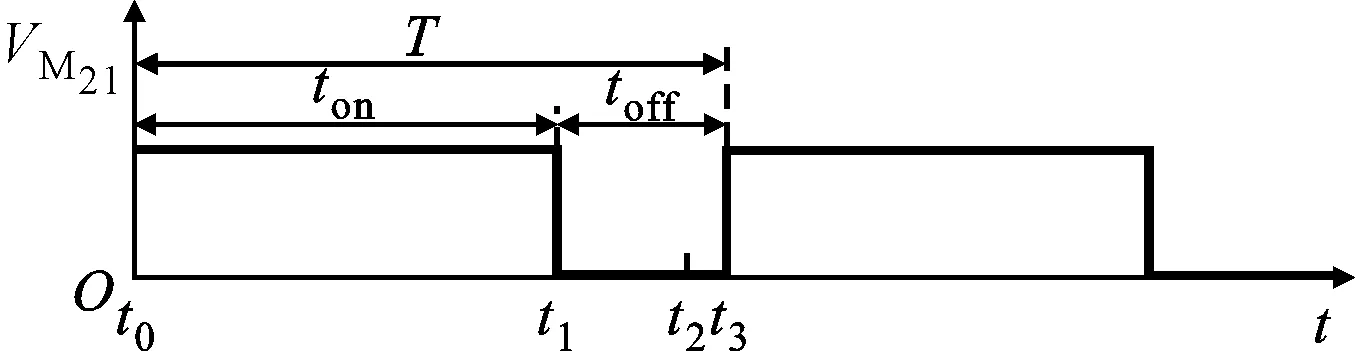
(a)MOS管M21上的电压波形

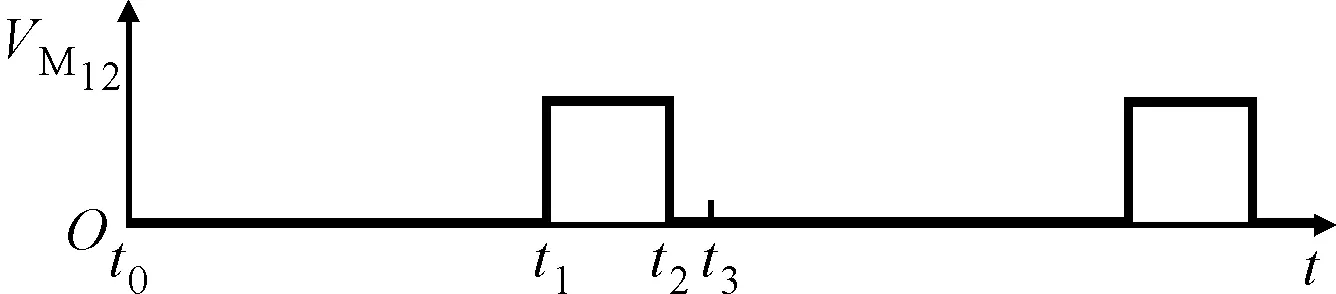
(b)MOS管M2上的电压波形

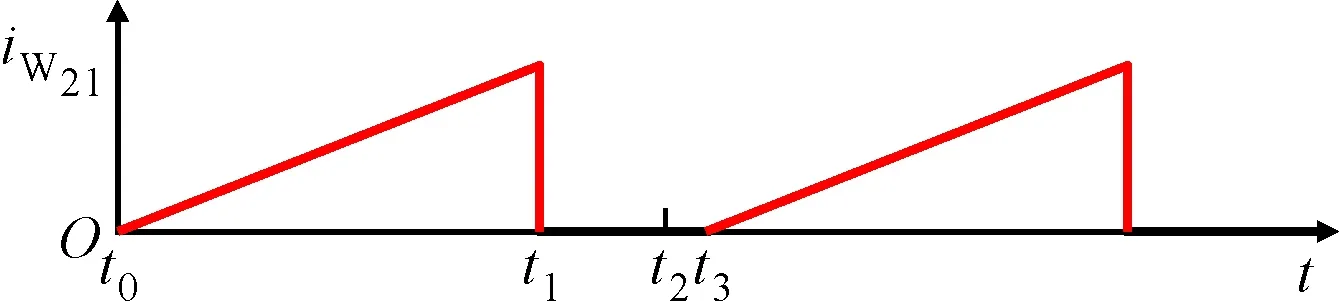
(c)变压器T2二次侧绕组L21上的电流波形

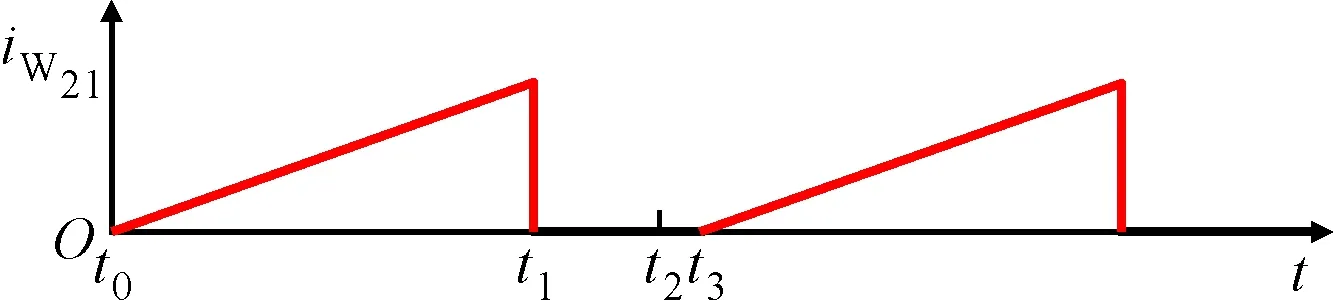
(d)变压器T2二次侧绕组L22上的电流波形

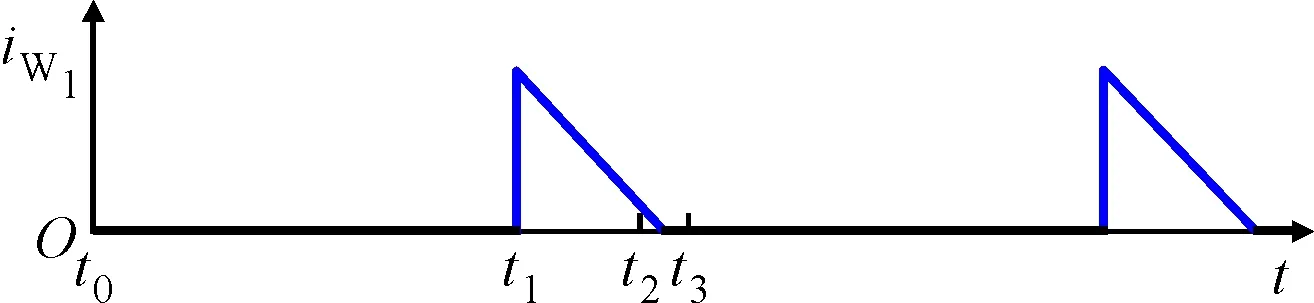
(e)变压器T2一次侧绕组L2上的电流波形图4 电池单元向电池组放电关键波形

由于均衡在DCM条件下进行,初始电流为0,通过求解一阶微分方程(14)和(15),可得电池C21和C22的放电电流为

(17)

(18)

从式(17)和(18)可看出,电池放电电流与其端电压存在正比关系,即电压越高的电池放电电流越大,与均衡结构设计一致。

在t=t1时刻,电池C21和C22的放电电流达到峰值

(19)

(20)

第2阶段(t1-t2):如图4b所示,t1时刻,M21和M22关断的同时导通M2,电流路径如图5b所示。根据安培环路定则,此时,变压器T2具有峰值电流IW2,peak为

N21iW21,t1+N22iW22,t1=N2IW2,peak

(21)

式中:N21和N22为绕组W21和W22的匝数;N2为绕组W2的匝数。

根据基尔霍夫电压定律在变压器T2一次侧的放电回路中的应用,可得

(22)

式中:VW2为一次侧绕组W2的端电压。

如图4e所示,根据回路初始电流iW2,t1,可得流经绕组W2电流

(23)

第3阶段(t2-t3):如图5c所示,所有MOS管关断,保证均衡运行在DCM中。

3 均衡控制策略

均衡控制策略是通过判断电池组中电池的状态,选取对应的均衡工作模式,进而控制相应MOS管的通断,达到均衡电池状态的目的。首先设定电压允许差值V0=0.02 V,然后,

根据检测到的电压

(a)第1阶段(b)第2阶段(c)第3阶段

图5 电池单元向电池组放电均衡过程分析信息估算电池单元与电池组的电压状态,最后根据电压状态判断是否需要均衡及应当采取的均衡模式。

均衡模式的选取依据是电池组与电池单元的电压差,具体的控制流程如图6所示。Vave,p表示电池组的电压状态,Vave,i(i=1,2,…,n)表示各个电池单元的电压状态,当电池组与电池单元间电压状态差值小于设定允许差值V0时,说明电池状态满足一致性要求,不执行均衡命令。当电压状态差值大于设定差值,即|Vave,p-Vave,i|>V0时,说明电池状态不一致程度较大,需要实施均衡。进一步,根据电池组与电池单元电压状态的大小关系,判断需要采取的均衡模式。当电池组电压状态大于电池单元电压状态,即Vave,p-Vave,i>V0时,说明电荷需要从电池组转移至电池单元,则采用电池组向电池单元充电的均衡模式;否则电荷需要从电池单元想电池组转移,采用电池单元向电池组放电的均衡模式。经过一次均衡循环后,继续根据检测到的电压信息判断是否需要均衡及需要采取的均衡模式,直至电池状态达到一致性要求,即电池组中电压差小于设定允许电压差。

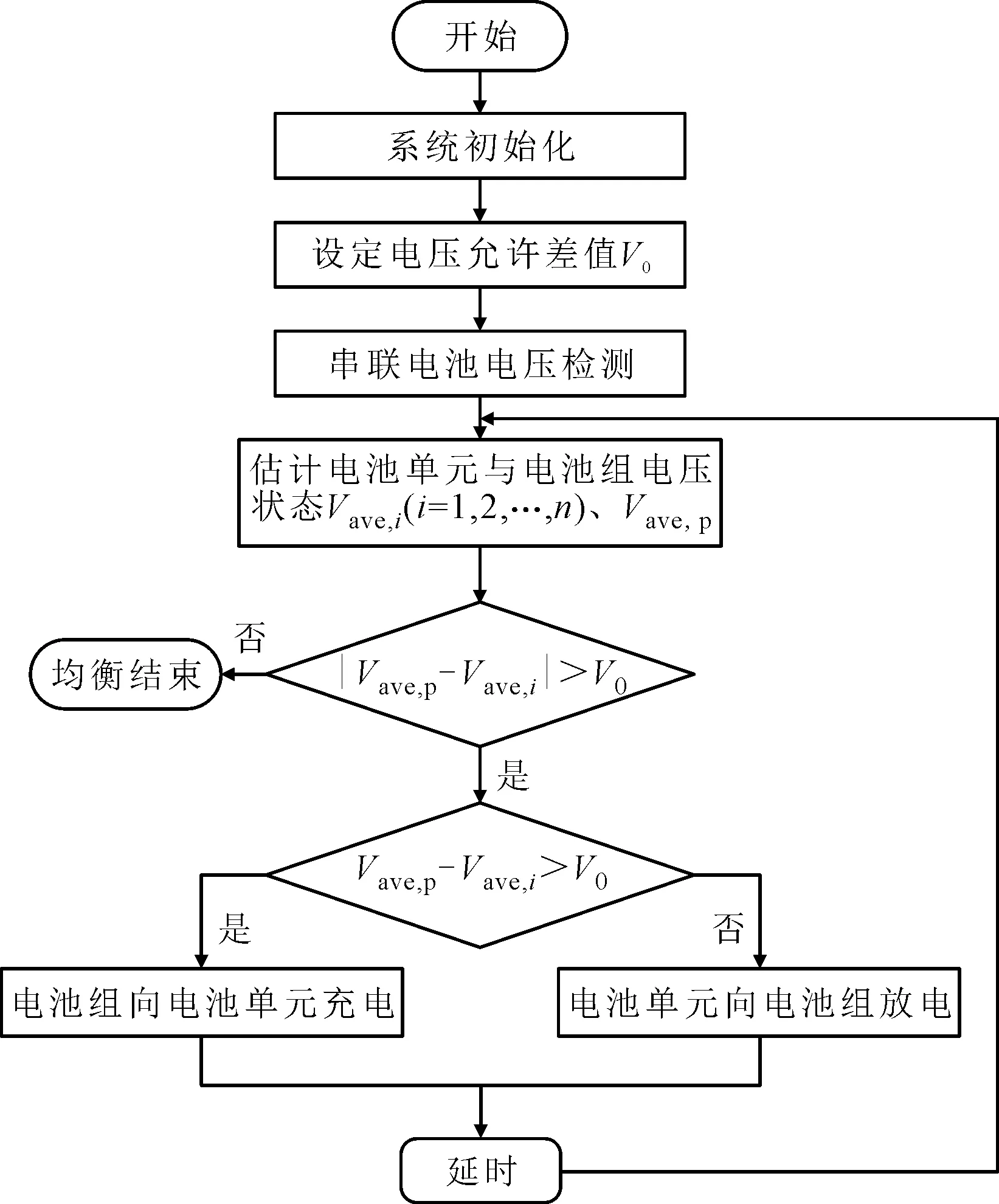
图6 均衡控制流程

从图6中可以看出,控制策略中包括两种均衡工作模式,与本文提出的均衡结构相匹配。因此,采用所提出的均衡方法和控制策略,能够根据电池状态选择适当的均衡模式。

4 实验验证

4.1 实验平台

为了验证所提出的均衡方法和控制策略,搭建了电池均衡实验平台。实验原理如图7所示。首先,将测试电流数据写入控制器。均衡过程中,信号采集电路将电池组的电压信息通过CAN发送至控制器,控制器根据信息判断均衡模式并发出PWM信号控制均衡电路对电池实施均衡。与此同时,控制器将电池测试数据利用RS485发送至程控电源与电子负载,根据测试电流数据的正负,交替控制程控电源对电池组进行充电或控制电子负载对电池组进行放电,使得电池在模拟工况下充放电。上位机实时显示电池状态。

图7 电池均衡原理图

电池均衡实验平台如图8所示。将4节容量为2 900 mA·h、电压范围为2.5～4.2 V的NCR 18650电池串联形成电池组,分为两个电池单元;变压器采用PC44材料的PQ20/20型,一次侧与二次侧绕组电感值分别为66.667 μH和8.473 μH;开关采用频率为25 kHz的IRF540N型MOS管。

图8 电池均衡实验平台

4.2 电池均衡实验验证

在所搭建电池均衡控制实验平台的基础上,首先在电池静置的情况下对电池组实施均衡,实验结果如图9所示,4节电池C11、C12、C21、C22初始电压分别为3.687、3.586、3.365和3.236 V。初始电压差较大,均衡过程中,高电压电池的电压逐渐下降,低电压电池的电压逐渐上升。均衡后,电池电压分别为3.457、3.453、3.445和3.443 V,电池电压差值小于设定的允许电压差,均衡效果明显。

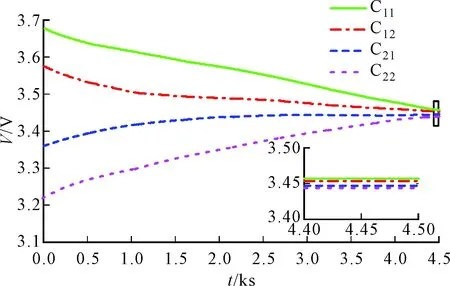
图9 静置状态下的均衡

综合考虑均衡初始、最终电压差及均衡时间等因素,定义单位时间的均衡速度为

(24)

式中:V0和VT分别为均衡初始和最终电压差;T为均衡时间。

采用本文均衡方法经过4.5 ks的均衡,电池组最大压差从451 mV降至14 mV,均衡速度为0.097 mV/s。将现有的多种均衡方法均衡速度进行对比:文献[19]经过6.12 ks的均衡,电池组最大压差从260 mV降至20 mV,均衡速度为0.039 mV/s;文献[17]虽然均衡时间为2.34 ks,但电池组最大压差仅从初始的24.1 mV降至最终的13.3 mV,均衡速度为0.005 mV/s;文献[20]电池组电压变化明显,最大压差从531 mV降至8 mV,但均衡用时17.49 ks,均衡速度为0.030 mV/s。相比较而言,结合变压器正反激原理的均衡方法具有较快的均衡速度和良好的均衡效果。

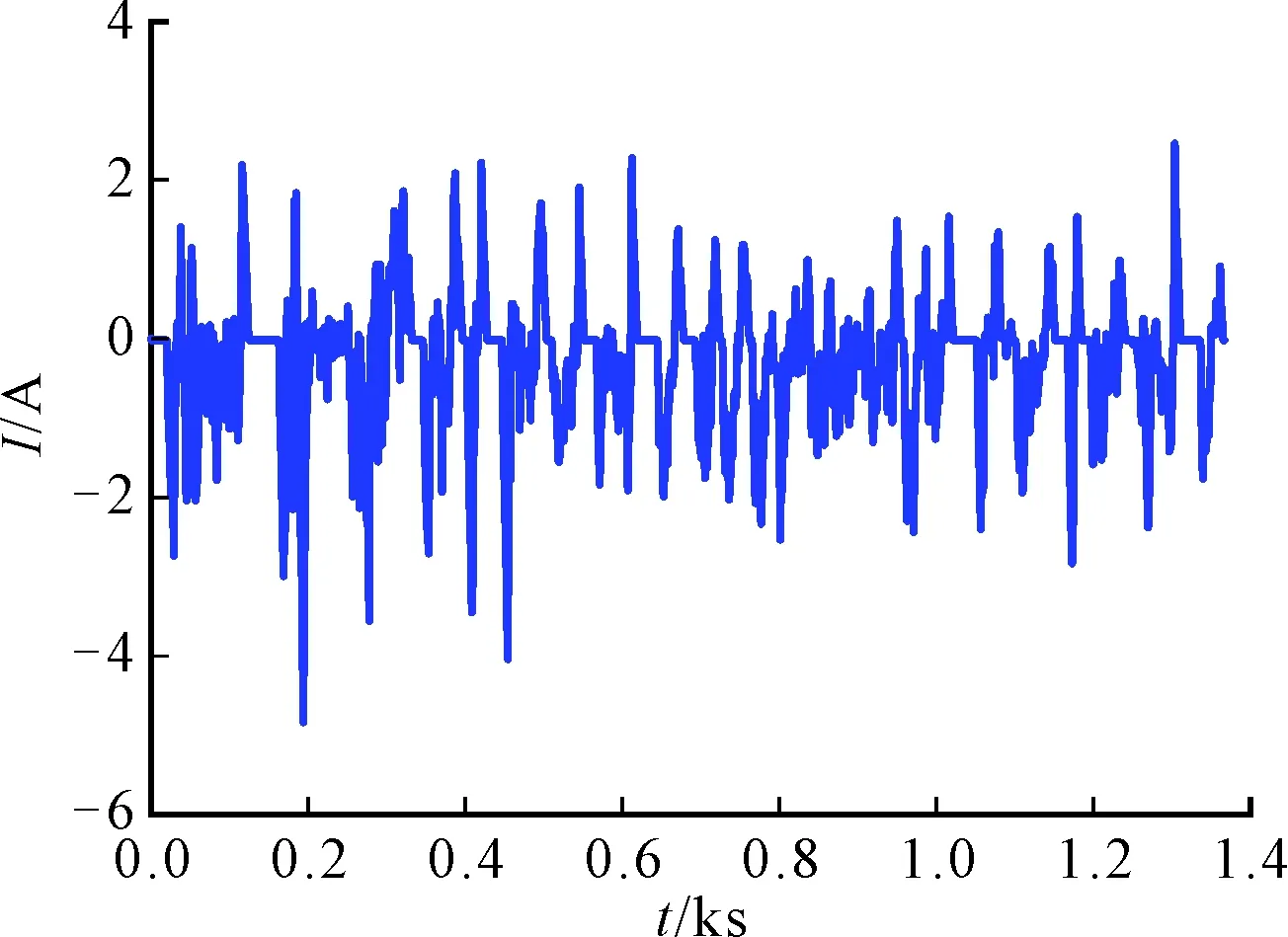
图10 UDDS测试电流曲线

进一步验证提出的均衡方法在电动汽车用电池使用过程中的均衡效果,引入美国城市循环工况(UDDS)对电池进行充放电,模拟电池实际使用过程。UDDS测试电流曲线如图10所示。均衡实验过程中,电池电压在UDDS测试过程中随着UDDS测试电流上下波动,结果如图11所示。

由图11可知,4节电池初始电压分别为4.014、3.953、3.879和3.820 V。当均衡持续约4 300 s后,4节电池的最终电压分别为3.653、3.650、3.645和3.641 V。在均衡过程中,电池间的电压差逐渐减小,最大电压差从初始的0.194 V降为0.012 V,小于设定的允许电压差。因此,所提出的电池均衡方法能够实现良好的均衡效果,可有效解决电池不一致问题。

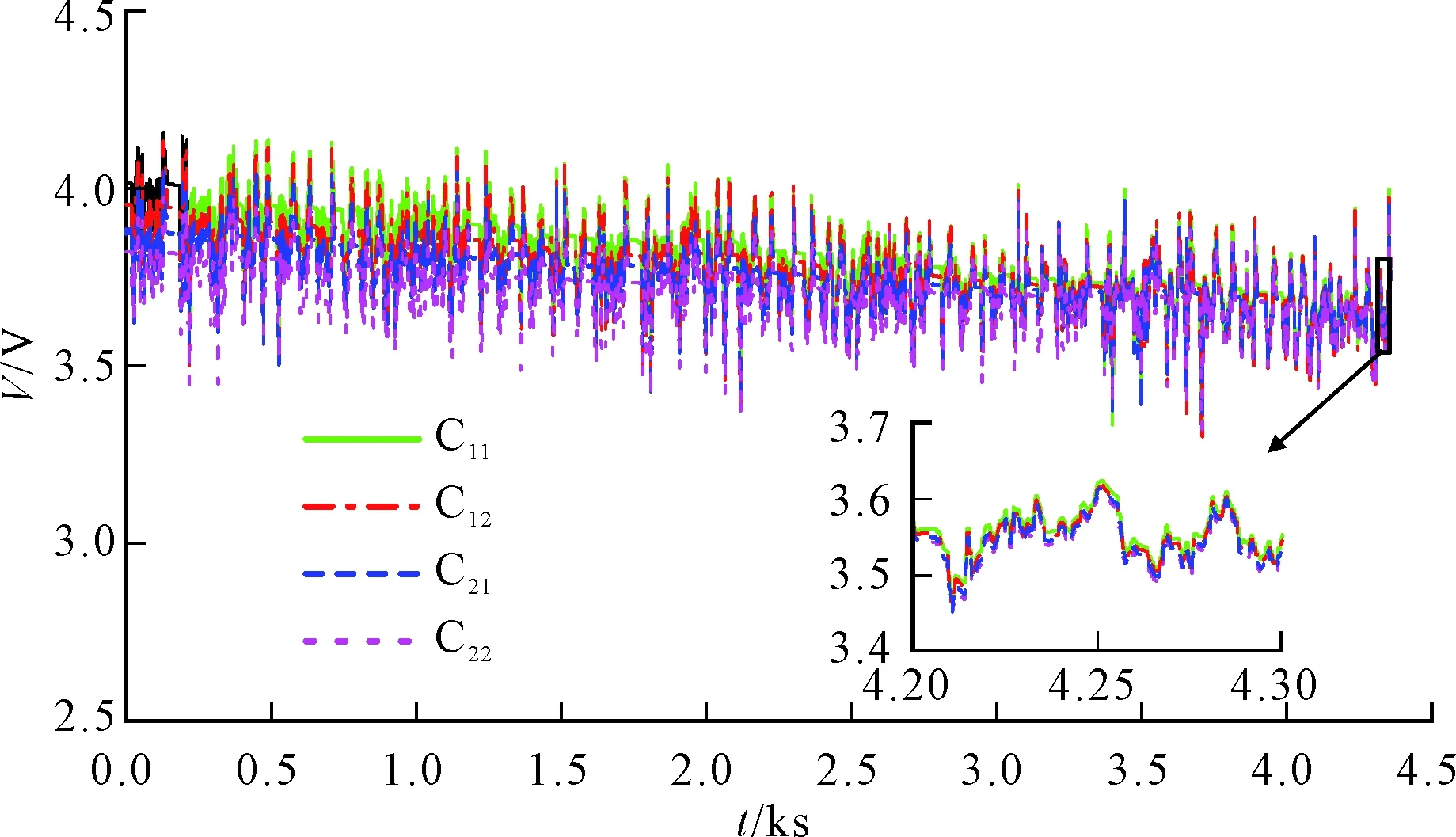
图11 UDDS测试条件下的均衡

5 结 论

针对电动汽车动力电池不一致问题,本文提出了一种结合变压器正反激原理的主动均衡方法。首先,设计模组化的均衡电路,实现变压器正反激原理相结合的均衡功能;然后,分析两种均衡模式的工作原理,并结合相应的控制策略,实现两种均衡模式的自动选择;最后,为了验证本文提出的动力电池主动均衡方法的有效性,搭建电池均衡实验平台,分别在静置和UDDS测试条件下,模拟动力电池实际工况。实验结果表明,大约经过4 ks,动力电池组便可实现均衡。与相似类型的几种均衡方法比较,提出的结合变压器正反激原理的主动均衡方法能够在元器件少、控制复杂度低的前提下达到更快的均衡速度。