采用长时间相参积累技术的高速机动目标检测快速算法

黄响,张林让,唐世阳

(西安电子科技大学雷达信号处理国家重点实验室,710071,西安)

随着科学技术的不断发展,越来越多的高速目标出现在雷达探测领域[1-3]。这些目标具有高超音速、强机动性和小雷达散射截面积等典型特点,如美国的SR-71战略侦察机可以实现马赫数为3的高速飞行;以X-43A为代表的高超飞行器加速度可以达到10g。传统的雷达检测方法面临着距离徙动和多普勒徙动等重大挑战,尤其是强机动性下多普勒徙动的复杂表现形式加剧了目标检测的难度。如何针对上述问题实现高速机动目标的快速检测,是当前雷达探测领域亟需解决的问题[4-5]。

在目前的高速目标检测算法中,楔石变换(KT)[6-7]和雷顿-傅里叶变换(RFT)算法[8-10]最为成熟。它们均能在低信噪比下实现线性距离徙动的校正和目标能量的有效积累,但无法解决因目标机动性而造成的高阶距离徙动和多普勒徙动问题,所以只局限于高速匀速目标的检测。针对匀加速运动的高速目标,许多学者在KT和RFT变换的基础上,提出了很多有效算法[11-16],如雷顿-分数阶傅里叶变换(RFRFT)[12]、楔石-去调频(KT-DP)[14]和KT-RFT[16]等。这些算法的主要思想是将多普勒徙动的补偿转化为线性调频信号的检测和估计,但对于强机动目标,加加速度带来的影响不可忽略。

针对加加速度的运动模型,文献[17]提出的雷顿-分数阶模糊函数(RFRAF)算法可以实现距离徙动和多普勒徙动的同时校正,但它需要距离、速度、加速度、加加速度以及分数阶傅里叶变换阶数这5维参数空间的同时搜索,运算量巨大。文献[18]提出的广义楔石变换-广义去调频(GKT-GDP)算法可以实现距离徙动与多普勒徙动的分步校正,但仍需要加加速度、加速度及速度模糊数的参数搜索,运算量依旧很大。为了实现高速机动目标的快速检测,文献[19]首先利用时间反转变换(TRT)实现线性距离徙动与三阶距离徙动的校正,再利用二阶楔石变换(SKT)实现二阶距离徙动的校正,最后转换到距离时域利用吕氏分布(LVD)实现多普勒徙动的校正和目标能量的积累。然而,这种TRT-SKT-LVD算法的运算流程过于复杂,且SKT变换会造成性能损失,同时LVD也会受到冗余信息和参数估计范围的限制[20]。

本文在以上研究的基础上,提出一种新的基于长时间相参积累的高速机动目标快速检测算法。首先在距离频域-慢时间域利用慢时间反转变换校正线性距离徙动、三阶距离徙动和多普勒徙动,再构造距离频域-慢时间域二次相位补偿函数,并利用能量积累函数实现二阶距离徙动和多普勒徙动的同时校正,最后在距离-多普勒域实现目标能量积累。相比于RFRAF和GKT-GDP算法,本文所提算法极大地降低了运算复杂度;相比于TRT-SKT-LVD算法,本文算法简化了操作流程,避免了因插值运算造成的性能损失,且不受到雷达回波冗余信息和运动参数估计范围的限制。

1 高速机动目标信号模型

假设脉冲多普勒雷达发射的波形为线性调频信号,则该脉冲串信号可表示为

(1)

式中:rect(·)是矩形窗函数;Tp、fc和γ分别表示发射信号的脉冲宽度、载频和调频斜率;tf∈[-Tr/2,Tr/2]和tm∈[-T/2,T/2]分别为快时间变量和慢时间变量;Tr和T分别表示脉冲重复周期和相参积累时间。

图1 高速机动目标的运动模型

假设运动场景中有K个带加加速度的高速机动目标,其相对雷达的运动模型如图1所示,其中:R0,k、V0,k、A1,k和A2,k(k=1,2,…,K)分别为第k个目标相对于雷达的初始距离、初始速度、初始加速度以及加加速度;θk(k=1,2,…,K)为第k个目标偏离雷达视线的角度。目标的斜距历程为

Rk(tm)=R0,k+V0,kcos(θk)tm+

(2)

假设在观测时间内θk不发生变化,定义v0,k=V0,kcos(θk),a1,k=A1,kcos(θk)和a2,k=A2,kcos(θk),其中,v0,k、a1,k和a2,k分别为第k个目标的初始径向速度、加速度和加加速度,则式(2)可简化为

(3)

雷达接收到的基带回波信号可表示为

exp[-j4πRk(tm)/λ]exp[jπγ(tf-2Rk(tm)/c)2]}

(4)

式中:σ0,k为第k个目标的散射系数;λ=c/fc为发射信号波长;c为光速。

对式(4)进行脉冲压缩处理可得

exp[-j4πRk(tm)/λ]}

(5)

式中:B为信号带宽;σ1,k为第k个目标经过脉冲压缩处理后的复数幅度。

式(5)的sinc函数项表示信号包络受慢时间的影响,即便在较短的积累时间下高速运动的目标也会使信号包络发生线性距离徙动现象;在长积累时间下,a1,k和a2,k也可能造成二阶及三阶距离徙动现象。同时,式(5)中的指数项表明目标的多普勒频率不再是一个定值。当a1,k和a2,k满足下式时,信号将发生二阶及三阶多普勒徙动现象

|2a1,kT/λ|>ρd; |a2,kT/(2λ)|>ρd

(6)

式中:|·|为绝对值运算;ρd=1/T为多普勒分辨率。距离徙动和多普勒徙动现象将使目标能量扩散在不同距离及多普勒单元中,从而导致雷达检测性能的大幅度下降。

2 徙动现象快速校正算法

若直接对Sc(tf,tm)进行处理,需要多维运动参数的联合搜索,运算量极大[8]。为了实现距离徙动的快速校正,首先运用快速傅里叶变换(FFT)将Sc(tf,tm)变换到距离频率-慢时间域,即

(7)

此时,距离徙动表现为距离频率f与慢时间tm的耦合,包括速度、加速度以及加加速度等复杂形式。要同时消除这种耦合,难度极大,这里提出一种分步去除方法,主要包括时间反转变换和频域二次相位补偿两大步,以下分别进行介绍。

2.1 慢时间反转变换

在文献[21]中,M个脉冲的慢时间序列为

(8)

将式(8)代入式(7)得

Sc(f,tm)=

exp[-j4π(f+fc)v0,k(-T/2,…,T/2)/c]·

exp[-j2π(f+fc)a1,k(-T/2,…,T/2)2/c]·

exp[-j2π(f+fc)a2,k(-T/2,…,T/2)3/3c]}

(9)

对慢时间序列进行反转可得

(10)

脉压信号Sc(f,tm)经时间序列反转后变为

Sc(f,tm←)=

exp[-j4π(f+fc)v0,k(T/2,…,-T/2)/c]·

exp[-j2π(f+fc)a1,k(T/2,…,-T/2)2/c]·

exp[-j2π(f+fc)a2,k(T/2,…,-T/2)3/3c]}

(11)

式(9)和式(11)具有以下两个特点:①慢时间序列奇数次幂的相位项是共轭的;②慢时间序列偶数次幂的相位项是相同的。利用这两个特点,构造如下的慢时间反转变换

Sn(f,tm)=Sc(f,tm)Sc(f,tm,←)=

(12)

exp[-j4π(f+fc)(R0,p+R0,q)/c]·

exp[-j4π(f+fc)(v0,p-v0,q)tm/c]·

(13)

由式(12)可知:对于单目标,经慢时间反转变换后,由速度引起的一阶距离徙动、由加加速度引起的三阶距离徙动和多普勒徙动得以完全消除,只剩下由加速度引起的二阶距离徙动和多普勒徙动需要进一步校正,但对于多目标,时间反转变换的非线性会引进交叉项。关于交叉项对多目标检测造成的影响,将在2.3节予以详细分析。

2.2 二次相位补偿函数

为了校正由加速度引起的距离徙动和多普勒徙动,文献[19]提出用SKT变换和LVD分布两步处理的方法,但该方法操作繁杂,运算量大,同时SKT变换因为插值运算会造成性能损失,LVD分布需要至少1 s的冗余信息并且受到参数估计范围的限制[20]。本文利用一步处理法即二次相位补偿函数法进行校正,其主要思想是通过构造距离频域-慢时间域的二次相位补偿函数将目标能量集中在同一变换单元中上,再利用能量积累函数估计出加速度的值。构造的二次相位补偿函数定义为

(14)

式中:as,k∈[-amax,amax]为目标的搜索加速度;amax为搜索加速度的最大值。

将式(12)与式(14)相乘可得

S(f,tm;as,k)=Sn(f,tm)C(f,tm;as,k)=

Scross(f,tm)}

(15)

由于构造的频域二次相位函数为线性变换,因此不会引入交叉项。为了分析方便,接下来的分析将不再继续考虑交叉项。

沿快时间维对式(15)作快速逆傅里叶变换(IFFT)得

S(tf,tm;as,k)=

(16)

由式(16)可知,当搜索的加速度与目标真实的加速度相匹配时,目标能量将集中于同一个距离单元中,此时,能量积累将达到最大值。因此,可构造如下能量积累函数对加速度进行估计

(17)

目标的加速度可按下式估计

(18)

由式(16)可知,对加速度的估计将会影响距离徙动和多普勒徙动的补偿。假设Δak=a1,k-as,k,则当

ΔakT2/4>ρr; 4ΔakT/λ>ρd

(19)

时,剩余的距离徙动和多普勒徙动将会使雷达的检测性能遭受损失,其中ρr=c/(2B)为雷达的距离分辨率。相比于距离徙动,多普勒徙动更易发生,因此在选取as,k的搜索间隔时,可以多普勒分辨率作为参考标准,联合大步长的粗搜索和小步长的精搜索,实现精确的加速度估计。

在获取精确的加速度估计值之后,匹配的频域二次相位补偿函数变为

(20)

按式(15)对剩余的距离徙动和多普勒徙动进行补偿,并将信号变为距离-多普勒域可得

(21)

在距离频率-多普勒域中,目标能量被积聚在同一个距离-多普勒单元中,且多普勒单元始终位于频率为0处。利用CFAR技术对S(tf,fm)进行处理,即可完成目标的检测[14]。

2.3 交叉项影响分析

多目标情形下,慢时间反转变换因其非线性会产生交叉项,交叉项的数学表达式如式(13)所示。由于二次相位补偿函数及后续的IFFT、FFT变换处理均为线性变换,不会再次产生交叉项,因此分析交叉项对多目标检测的影响时,可采用式(13)。由式(13)可知,交叉项对自聚焦项的影响决于多目标的运动参数,具体表现如下。

(1)当多目标位于不同的距离单元时,信号交叉项的能量会分散在与自聚焦项不同的距离单元中,其他运动参数的差异更会使交叉项的能量进一步分散在不同的多普勒单元中,从而不会对多目标的检测造成很大影响。

(2)当多目标位于同一距离单元时,信号交叉项的能量积累受其他运动参数制约,具体有3种表现方式:①当多目标的径向速度和加加速度不完全相同时,信号的交叉项无法完全消除速度带来的线性距离徙动和加加速度造成的距离徙动及多普勒徙动,从而造成能量分散不同的多普勒单元中,对自聚焦项的影响较小;②当多目标的径向速度和加加速度完全相同,但加速度的大小不同时,式(14)构造的二次相位补偿函数会进一步根据加速度的差异对多目标进行有效检测;③当多目标的径向速度和加加速度完全相同,加速度的大小相等,但方向相反时,交叉项能量会聚集在同一距离-多普勒单元中,影响多目标个数的判断,但此时交叉项对应二次相位补偿函数的搜索加速度为零,因此可根据加速度的值作进一步甄别,确定多目标的真实个数。

(3)当多目标之间的散射系数相差很大时,由运动参数相同而造成的交叉项对自聚焦项的影响很大,此时可以采用CLEAN技术进行处理[14]。

综上分析,在一般多目标的运动场景下,时间反转变换可以有效地抑制交叉项对自聚焦项的影响,构造的二次相位补偿函数也会进一步地实现多目标的分离,从而实现多目标的检测。

3 算法实现及运算量分析

3.1 算法实现

本文所提算法的具体实现步骤如下。

(1)对接收的雷达回波进行下变频、脉冲压缩并沿快时间维进行FFT,得到回波距离频域-慢时间域数据Sc(f,tm)。

(2)将Sc(f,tm)沿慢时间序列反转得到Sc(f,tm,←),构造时间反转变换Sn(f,tm)以校正线性距离徙动、三阶距离徙动和因加加速度造成的多普勒徙动。

(3)根据高速机动目标的先验信息确定加速度的搜索范围[-amax,amax],搜索间隔采用变步长法,即先采用大步长确定加速度的粗估计值,再采用小步长确定加速度的精估计值。

(5)用估计的加速度构建匹配的频域二次相位补偿函数C(f,tm),校正由加速度引起的二阶距离徙动及多普勒徙动。

(6)将步骤(5)补偿后的信号沿距离频率维作IFFT变换,并沿慢时间维作FFT变换,得到距离-多普勒域数据S(tf,fm);利用恒虚警技术对S(tf,fm)检测单元矩阵进行处理,以判定目标是否存在。

3.2 运算量分析

为了进一步说明本文所提算法在运算量上的优势,采用TRT-SKT-LVD、RFRAF和GKT-GDP算法进行对比分析。假设积累的脉冲个数为M,距离单元数为N,时延采样点为Nd,搜索的速度数、加速度数、加加速度数和分数阶傅里叶变换的阶数分别为Nv、Na、Nk和No。由于时间反转变换的复杂度为O(MN),构造频域二次相位补偿函数的计算复杂度为O(NaMNlbN),因此本文所提算法的计算复杂度为O(NaMNlbN);TRT-SKT-LVD算法的计算复杂度为O(5NdNMlbM+NdNMlbN+2MNlbN+NM2+NM);RFRAF算法的计算复杂度为O(NvNaNkNoNMlbM);GKT-GDP算法的计算复杂度约为O(NaNkNMlbM)。假设M=N=Nd=Nv=Na=Nk=No,则本文所提算法、TRT-SKT-LVD、RFRAF和GKT-GDP算法的计算复杂度分别为O(N3lbN)、O(6N3lbN)、O(N6lbN)和O(N4lbN)。这充分证明了本文所提算法具有较高的运算效率。

4 仿真实验及分析

雷达系统参数设定为:载频fc=10 GHz,带宽B=20 MHz,脉冲宽度Tp=10 μs,脉冲重复频率fr=200 Hz,采样频率fs=80 MHz,脉冲积累个数M=401。

实验1验证本文所提算法的仿真性能。仿真场景中有3个运动目标,它们的运动参数设置如表1所示。本文算法的仿真结果如图2所示。图2a中的脉冲压缩结果表明,由于运动目标的高速强机动性,目标脉冲压缩后的能量不再积聚在同一个距离单元中,会出现严重的距离徙动现象。图2b显示了慢时间反转变换后信号在距离时域-慢时间域的仿真结果,它表明慢时间反转变换会使目标信号的线性和三阶距离徙动得以补偿,只剩下因加速度引起的二阶距离徙动项;同时慢时间反转变换会引入交叉项,但交叉项的线性和三阶距离徙动却无法得以完全补偿。图2c为利用能量积累函数估计的加速度结果,从图中可以看出,这种方法能实现加速度的准确估计。图2d～图2e表明经频域二次相位补偿后,目标的二阶距离徙动得到有效补偿,目标的能量位于同一距离单元中,但交叉项的能量却依旧分散在不同的距离单元中,从而证明了构造的二次相位补偿函数可以进一步抑制交叉项的影响。图2f～图2g显示了各个目标在距离-多普勒域的脉冲积累结果。从图2中可以看出,目标能量积聚在同一个距离-多普勒单元中,形成峰值,而交叉项的能量却分散在不同的距离-多普勒单元中,从而证明本文算法可以有效地抑制交叉项的影响,实现多目标的检测。图2h显示了TRT-SKT-LVD算法的积累结果。由于LVD分布在此场景下失效,所以此方法无法实现目标能量的有效积累和目标的进一步检测。

表1 多目标运动参数表

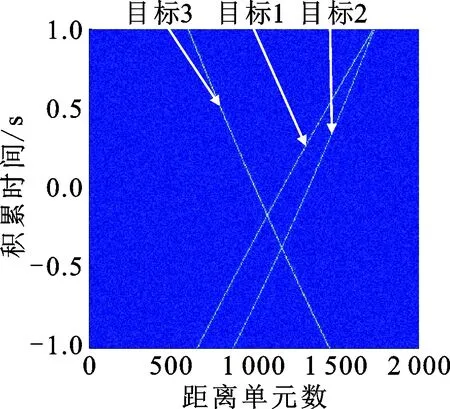
(b)慢时间序列反转变换

(c)加速度估计

v

(a)脉冲压缩(as=80 m/s2)

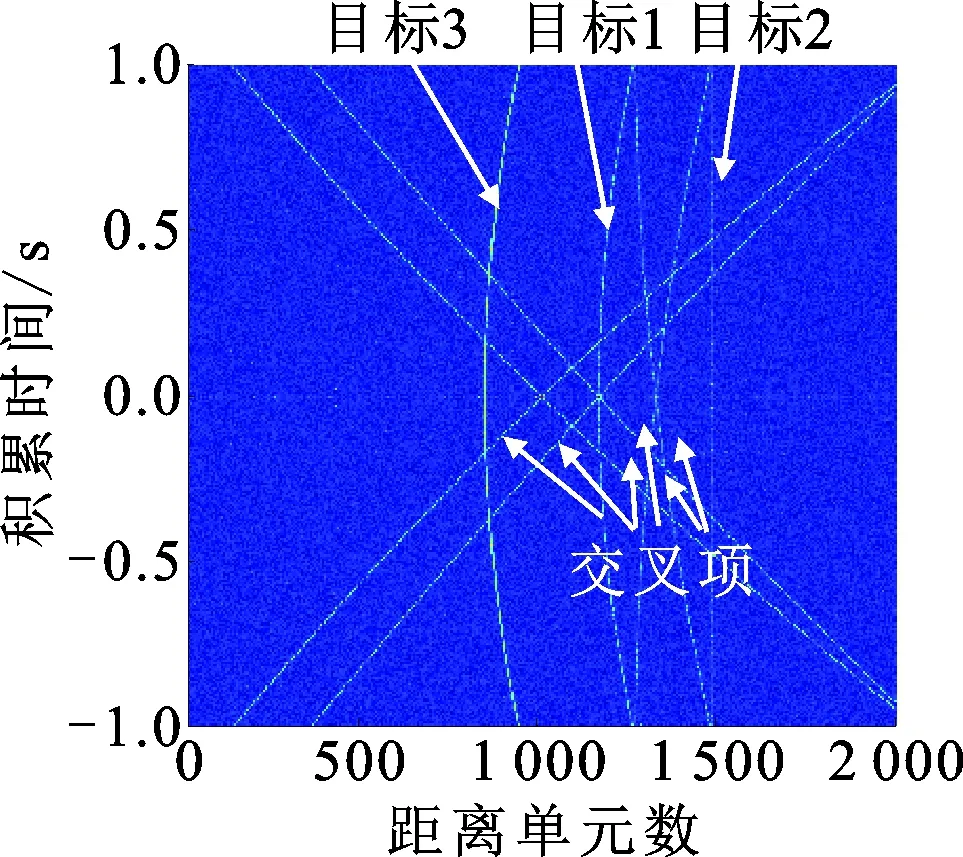
(e)二次相位补偿(as=-100 m/s2) (f)脉冲积累(as=80 m/s2) (g)脉冲积累(as=-100 m/s2) (h)TRT-SKT-LVD算法

图2 本文算法的仿真结果

实验2与其他方法运算时间的对比。仿真目标的运动参数与实验1中的目标1相同,计算机主要配置为CPU:Intel Core i7-4970 3.6 GHz;RAM:8 GB;操作系统:Windows 7;运行软件:MatlabR2012b。表2显示了本文所提算法与RFRAF、GKT-GDP、TRT-SKT-LVD算法的运算时间对比结果。由表2可见:由于RFRAF算法需要5维运动参数的同时搜索,因此消耗的运算时间巨大;GKT-GDP算法也是一种三维运动参数搜索过程,需要花费的时间也很大;虽然TRT-SKT-LVD算法不需要运动参数的搜索,但需要对每个距离单元进行LVD,消耗的时间也处于百秒级;与上述3种方法相比,本文所提算法的运算时间处于秒级,运算时间大大缩短,更加利于工程上的实时应用。

表2 4种算法的运算时间比较

图3 4种算法的检测性能曲线

实验3与其他方法检测性能的对比。仿真目标的运动参数与实验1中的目标1相同,虚警概率为10-4,脉压后的信噪比区间为[-10 20] dB,选取RFRAF、GKT-GDP和KT-DP算法作为对比,对每一个信噪比下的算法进行500次蒙特卡罗试验,得到的检测性能曲线如图3所示。由图3可见,相比于KT-DP算法,本文所提算法能够有效地补偿加加速度带来的三阶距离徙动和多普勒徙动,具有更优的检测性能。由于GKT-GDP算法需要3次KT变换,会造成严重的性能损失。同时,它涉及多步运动参数的估计,有较高的信噪比要求。所以本文所提算法的检测性能要优于GKT-GDP算法。由于RFRAF算法是基于运算参数的联合搜索,因此它的检测概率随信噪比的变化要缓于本文所提的算法,具有更强的抗噪性,但由实验2可知,RFRAF算法消耗的运算时间要远远大于本文所提算法。

5 结 论

高速机动目标在长相参积累时间内会发生复杂的距离徙动和多普勒徙动现象。针对该问题,本文提出一种快速校正算法。与现有算法相比,本文算法具有以下优点:①能够同时补偿因速度、加速度和加加速度造成的复杂距离徙动和多普勒徙动,适用的范围更广泛;②只需对加速度进行搜索,运算复杂度大大降低;③对多目标产生的交叉项能够有效抑制,可实现多个目标的检测;④多普勒模糊问题对于目标检测没有影响。需要注意的是,时间反转变换是非线性运算,对回波信噪比有一定的要求。