变速重载设备齿轮箱轴承故障的改进阶次包络分析方法

2019-08-22何小高张庆贾林山赵津

西安交通大学学报 2019年8期

何小高,张庆,2,贾林山,赵津

(1.西安交通大学机械工程学院,710049,西安; 2.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)

变速重载设备如轧机、造粒机、风机、辊子等是冶金、石化、风电、造纸等生产线的核心组成部分[1]。由于此类设备工作环境恶劣,且常处于变速重载工况下运行,轴承作为主要的支撑部件,容易因疲劳磨损而发生局部故障[2-4],据统计,旋转机械中约有30%的机械故障由轴承引起。目前,对轴承状态监测的方法主要为振动信号分析方法[5-6],齿轮箱作为主要的传动装置,在运行时,由于啮合振动能量较大,频带较宽,极易对轴承故障引起的共振频带造成干扰,从而无法直接利用频谱和包络谱进行分析[7-8]。

针对上述问题,许多学者进行了研究。王平等提出了一种基于自适应除噪(ANC)和共振解调技术相结合的轴承故障诊断方法,针对齿轮振动引起的转频调制共振带的情况,通过ANC技术,对相同工况下正常和故障轴承的振动信号进行融合降噪处理,从而去除齿轮振动产生的噪声,但工业应用场景难以得到完全相同工况下的正常信号,导致该方法在实际应用中受限[9]。Borghesani等采用齿轮带通滤波降噪和时域逆采样的方式去除齿轮信号干扰,在对角域信号进行带通滤波时,存在带宽选取问题,且在一定程度上会削弱轴承故障冲击特征[10]。李红贤等采用迭代广义解调齿轮信号分离的方法对齿轮箱轴承进行诊断,在对变速信号使用峰值搜索算法提取峰值啮合倍频时,误差较大[11-12]。Wang等提出了改进的自适应降噪算法消除齿轮振动对轴承共振带的影响,以提取的瞬时故障特征频率曲线等效为轴承转频,进行重采样处理[13]。王义等提出一种基于阶比关系进行转速分离的变转速工况下的滚动轴承监测方法,但该方法需要对包络时频脊线进行提取,受人工干预较大[14]。Barbini等提出相位矫正的轴承故障诊断方法,基于轴承振动能量较齿轮能量低的原理,通过对振动信号的复频谱进行保幅移相处理,再通过逆傅里叶变换,对处理前后数据求残差,去除能量较大的齿轮振动的干扰,但该方法同时也会对幅值较小的噪声成分加强,产生新的干扰,不利于轴承故障的识别[15-16]。

现有研究思路均以消除齿轮振动对轴承故障的影响为目标,关心的信息为轴承故障引起的高频共振带。该类方法难以实现在不削弱轴承故障成分的情况下完全消除齿轮振动,且存在高频共振带无法准确选择的问题。

针对上述问题,本文提出了通过融合齿轮和轴承参数信息确定解调频带,并对多个频带的包络信号进行阶次平均处理,实现轴承故障检测的方法。先通过建立齿轮啮合动力学方程阐述了轴承故障和齿轮振动频带耦合作用机理;然后融合齿轮和轴承参数,提出利用轴承故障对齿轮振动调制和高频共振调制机理的不同特性,研究基于齿轮啮合频带能量排序的轴承故障识别方法;最后通过阶次包络平均处理,实现多段包络谱调制特征的融合,为齿轮箱轴承故障诊断提出了一个新的思路。

1 轴承故障对齿轮振动的调制机理

目前,对齿轮故障的研究往往聚焦于齿轮损伤及轴不对中等引起的平稳故障[17-18]。当一对啮合齿轮中的一个齿轮出现齿形误差、齿轮磨损、齿轮断裂等故障时,会引起齿轮周节在啮合位置处产生随转频周期变化的位移,从而产生位移激励。其特点主要为振动信号中出现齿轮啮合频率以转频及高次谐波为调制频率的复杂边频带。

除了上述情况之外,当齿轮轴承或毗邻轴承出现故障时,由轴承故障造成的对轴径和轴承座的周期性冲击脉冲力也会作用在齿轮上,引起和齿轮故障和轴故障类似的效果。

为了描述上述现象,研究齿轮啮合的动力学特性。设a和b为一对啮合齿轮的主动轮和从动轮,其等效半径分别为ra和rb,主动轮驱动转矩为Ta,从动轮的负载转矩为Tb,主动轮、从动轮的转动角速度分别为ωa、ωb,旋转角位移为θa、θb。主动轮和从动轮的质量分别为ma、mb,齿轮副之间的啮合刚度为k(t),啮合阻尼为c,则其齿轮啮合动力学模型可以等效为弹簧-质量-阻尼系统,如图1所示。

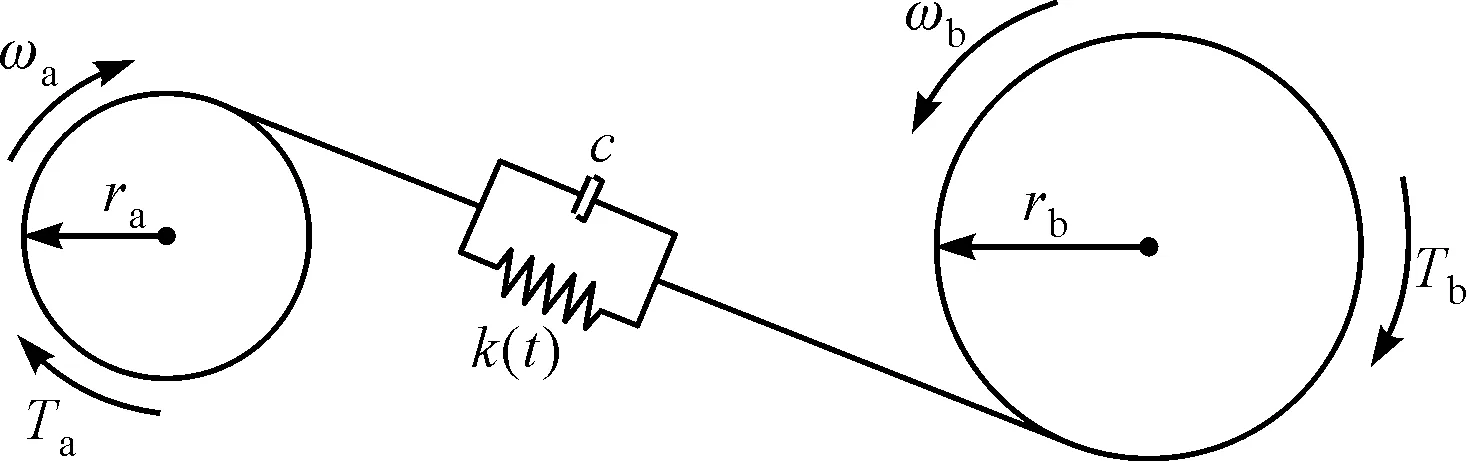
图1 齿轮啮合动力学模型

设齿轮啮合线上的相对位移为x,根据几何关系,有

x=raθa-rbθb

(1)

图1所示的啮合点处动力学方程如下

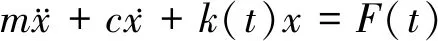
(2)

式中:m为当量质量;F(t)为外界激励。

在式(1)中,外界激励F(t)是系统的等效激振力,在润滑良好、不计齿面摩擦的情况下,主要受齿轮刚度和传动误差的影响,公式如下

F(t)=k(t)(e0+egcos(2πfrt)+ebcos(2πfbt))

(3)

式中:e0为齿轮受载后的平均静弹性变形;eg为齿轮磨损或齿形误差等引起的齿轮间相对位移变化的幅值;fr为转频;eb为齿轮轴承故障产生的冲击作用引起齿轮间位移变化的幅值;fb为轴承故障频率。

由于齿轮啮合过程中单、双齿交替变换,k(t)是时间t的周期函数,因此可以用傅里叶级数进行展开

(4)

式中:k0为平均啮合刚度;n为啮合频率倍频分量,n=1,2,3…;kn为啮合频率n倍频的幅值;fm为齿轮副的啮合频率;φn为啮合频率n倍频的相位。

将式(3)(4)代入到式(2),得

(e0+egcos(2πfrt)+ebcos(2πfbt))

(5)

为求解稳态振动频率成分,由于高阶傅里叶级数项系数较小,这里假设kn≪k0,忽略等式左边的高阶项,同时利用积化和差公式进一步简化,有

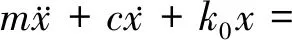
(6)

对于上述二阶线性系统,等式右边为输入激励,根据线性系统的同频特性,在系统的通频带内,系统的稳态输出频率和激励频率相同,仅幅值和相位有变化。因而,齿轮振动信号中将包含式(6)右边的频率成分,即转频fr、轴承故障频率fb及其与齿轮啮合频率及倍频的调制分量(nfm±fr)和(nfm±fb)。

因此,可以得出如下结论:和齿轮故障类似,当齿轮轴承或齿轮相邻轴承发生故障时,轴承故障频率会对齿轮啮合频率及其高次谐波进行调制,从而形成以轴承故障频率为调制频率的边频带,且边频幅值的大小和齿轮啮合振动能量kn相关。

2 轴承故障的改进阶次包络分析

2.1 变速重载齿轮箱的振动加速度信号特点

由于变速重载齿轮箱工作在转速变化的工况条件下,直接对其振动加速度信号进行傅里叶变换会导致谱分量的不断移动,造成频谱模糊现象,影响频谱分析,因此需要对其进行角域重采样。同时,由于齿轮箱中齿轮啮合刚度周期波动、齿轮齿形误差、轴承受载变化[19]、轴承故障等的影响,振动信号中频谱成分较为复杂,易出现齿轮啮合频率高次谐波和轴承故障引起的高频共振频带重叠现象,对共振带中的轴承故障信息造成干扰,且该频带本身存在难以确定的特点。

此外,由第1节机理分析可知,当齿轮和轴承发生故障时,在低频和齿轮振动频带处,会出现转频、轴承故障特征频率及其与齿轮啮合频率的调制成分,即轴承故障冲击在对高频共振带调制的同时,也会对齿轮振动啮合频带产生耦合作用,且该耦合作用随齿轮啮合振动能量协同变化。由于齿轮啮合刚度各谐波幅值的不确定性[20],尽管该频带具有大量的轴承故障信息,由于频带能量和谐波次序关系的复杂多变特点,难以直接确定分析频带。因此,对于该类设备,提出更加有效合理的频带选择方法具有重要的理论和实际意义。

2.2 改进阶次包络分析方法

针对上述问题,本文提出了融合齿轮、轴承参数的齿轮啮合频带选择和阶次平均的改进阶次包络分析方法,原理如图2所示。

总体分为如下3个步骤。

(1)阶次计算。传统阶次分析方法需要使用键相装置获得设备的等角度转速信息,在实际工业应用中,大多数设备存在没有安装或者缺少安装上述硬件条件的情况,容易从电机控制端获得异步采样的瞬时转速信号,其特点是相比振动加速度信号采样频率较低。由于变速重载设备一般工作在低速状态,转速变化相对较小,因此可以拟合得到完整平滑的转速曲线。通过对上述转频曲线积分,得到重采样的键相时标,计算过程如下

(7)

式中:Ti、i、θ分别为键相时标、等角度采样序列号、等角度采样间隔。

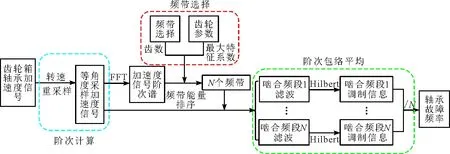
图2 改进阶次包络分析方法原理

通过求解式(7),可得等角度采样的键相时标Ti,采用线性插值方法对原始振动信号重采样,得到对应时标处的幅值为

(8)

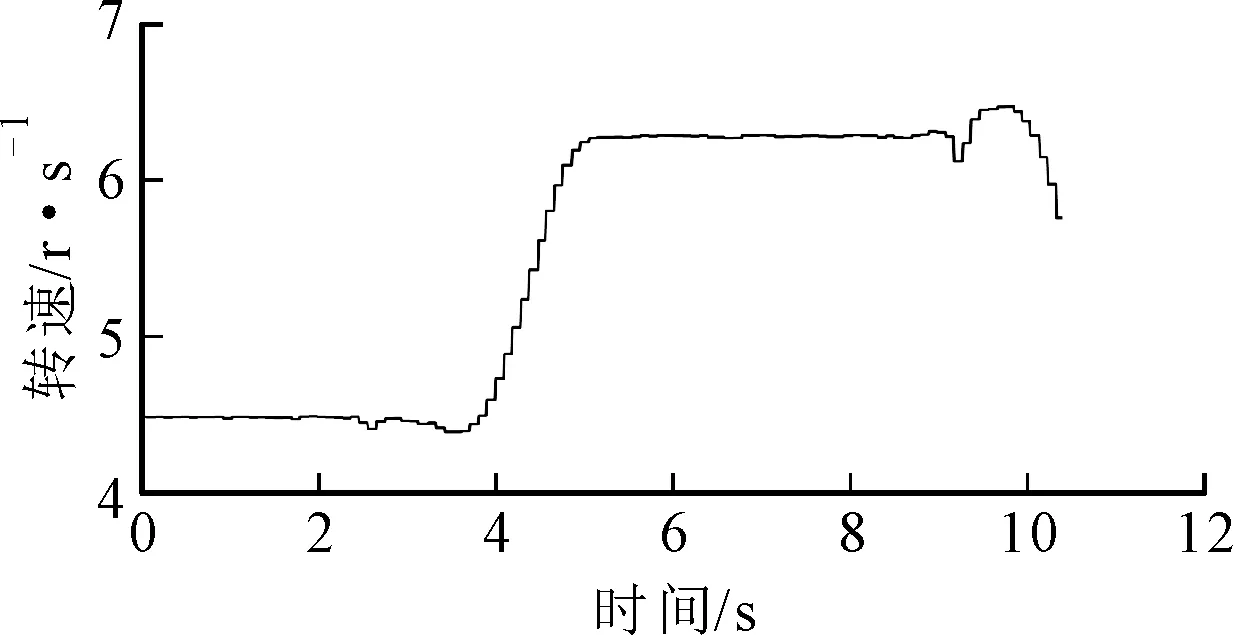
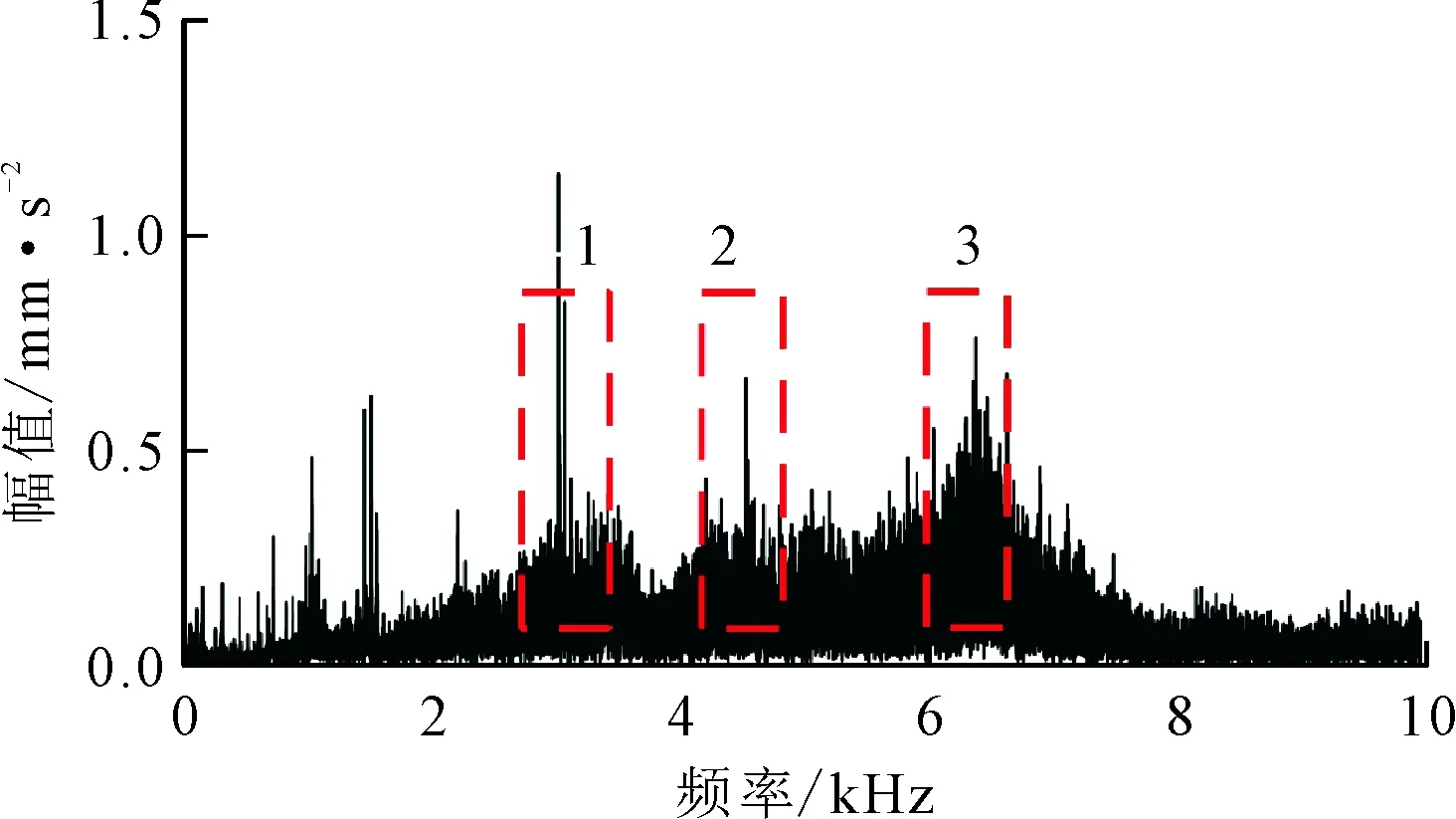
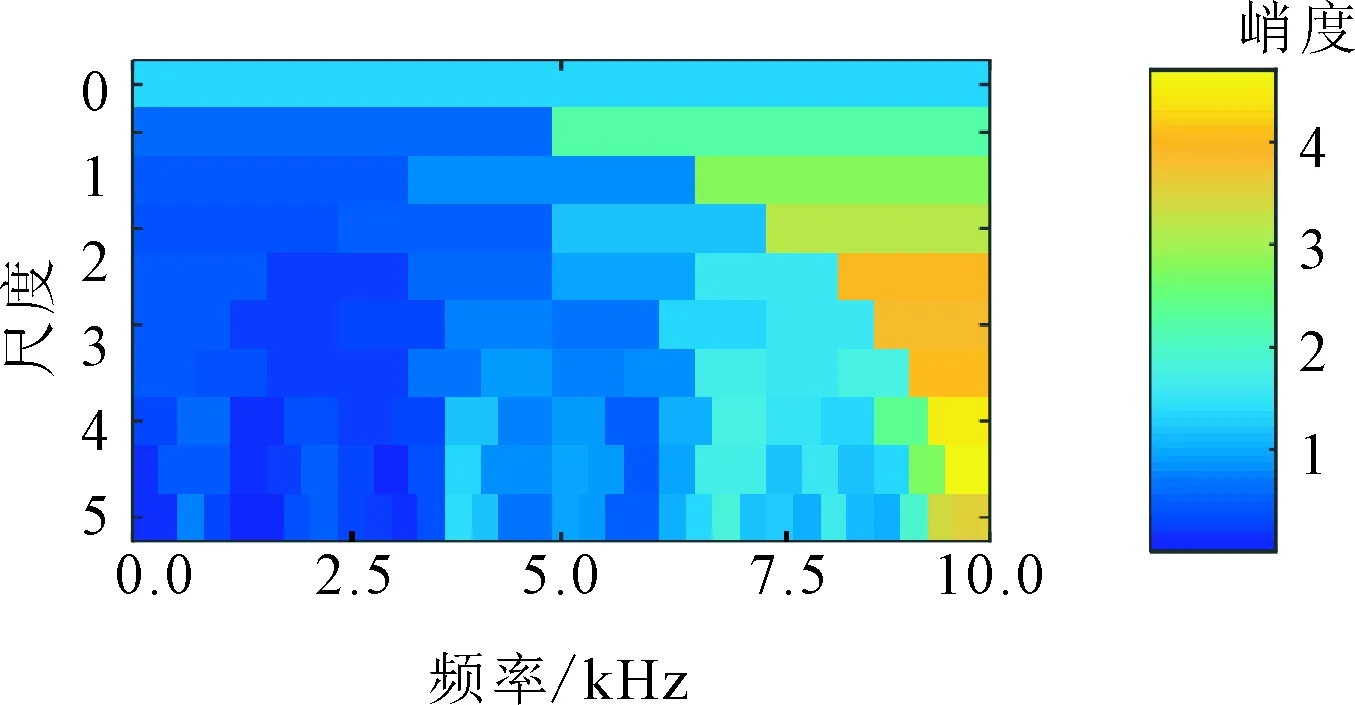
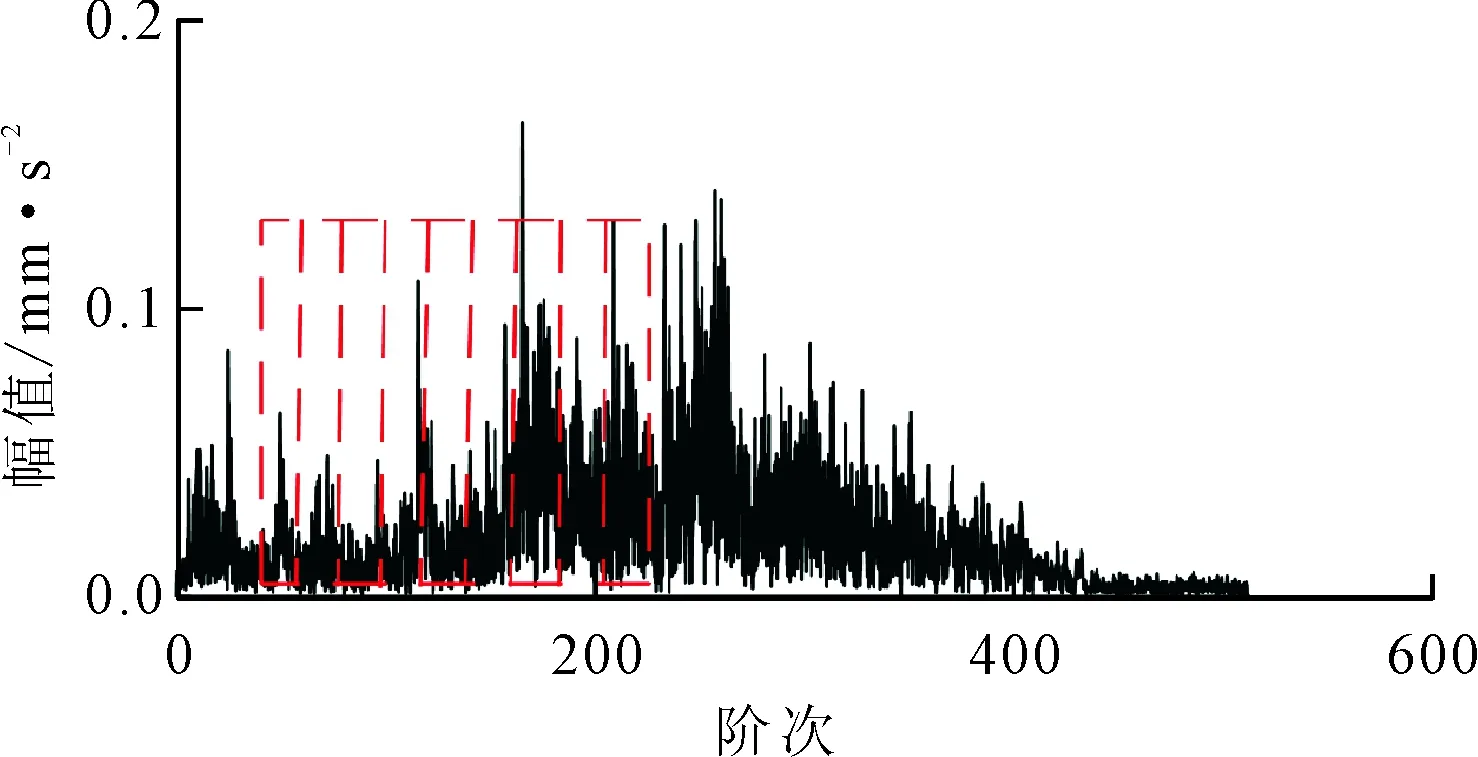
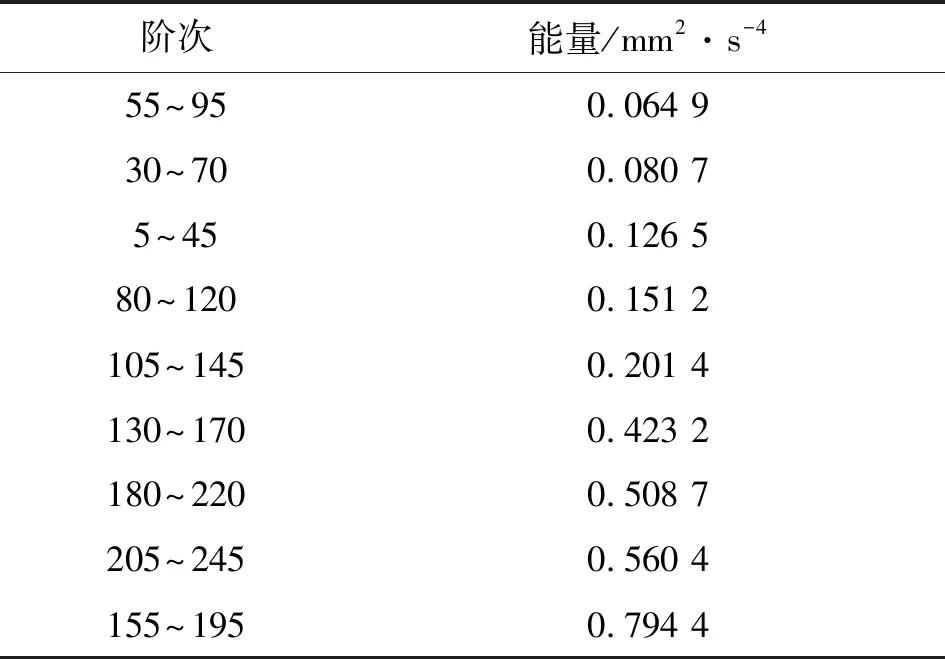
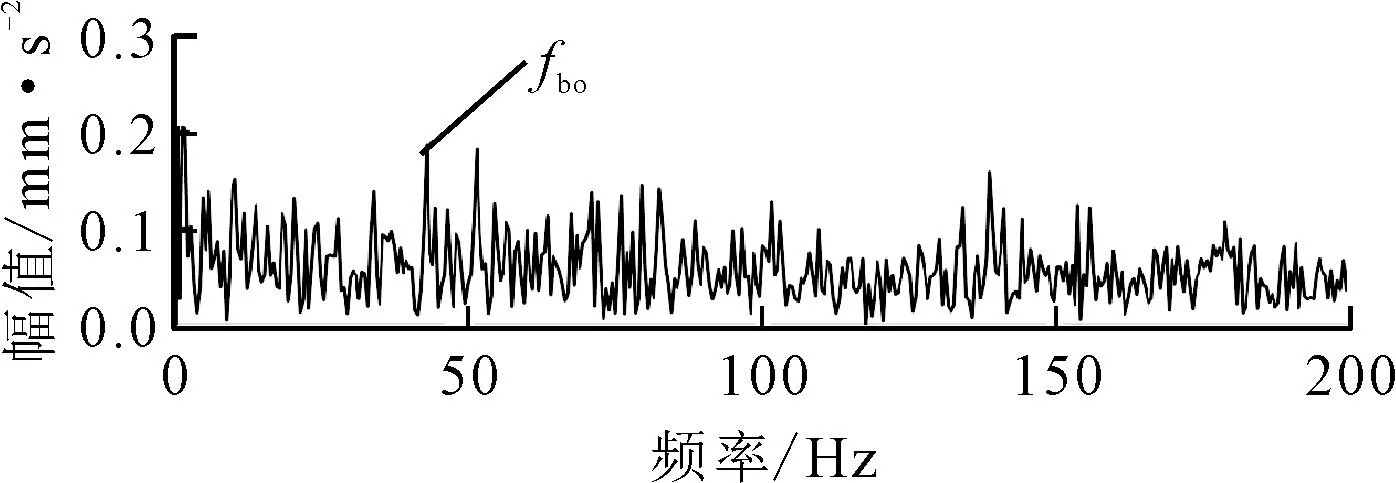
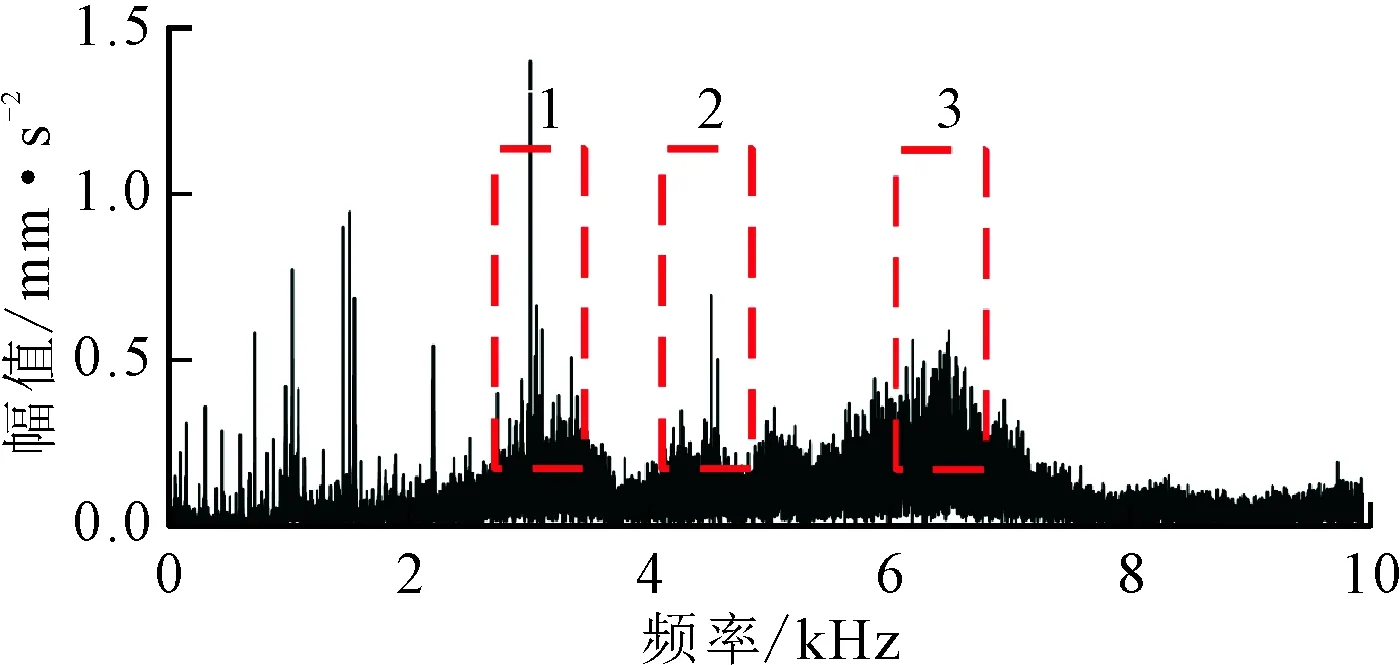
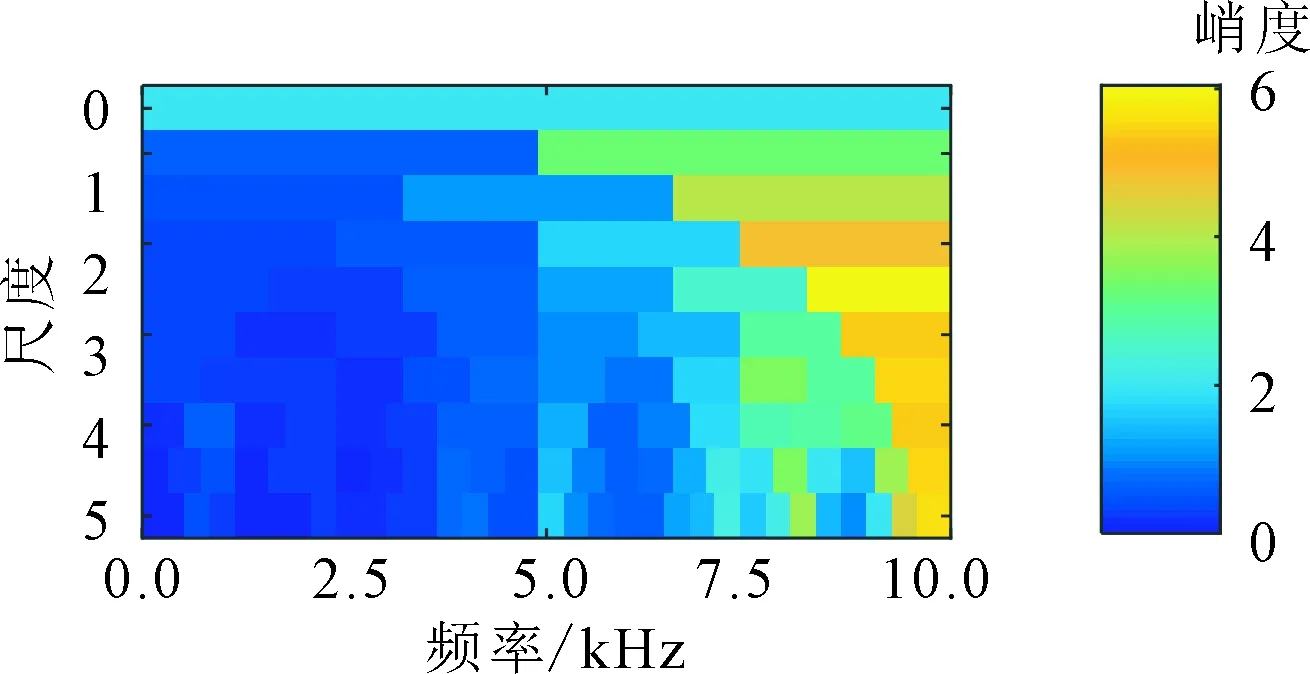
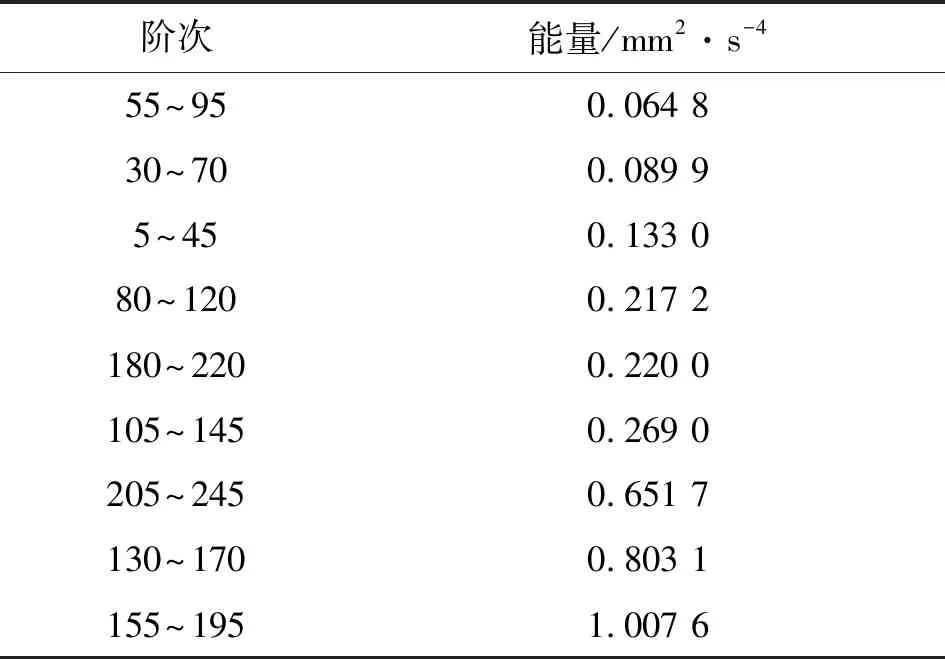
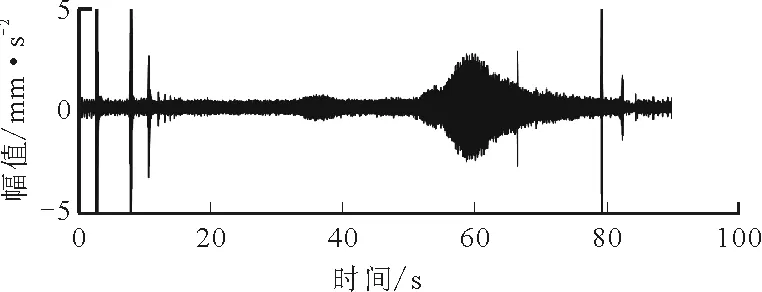
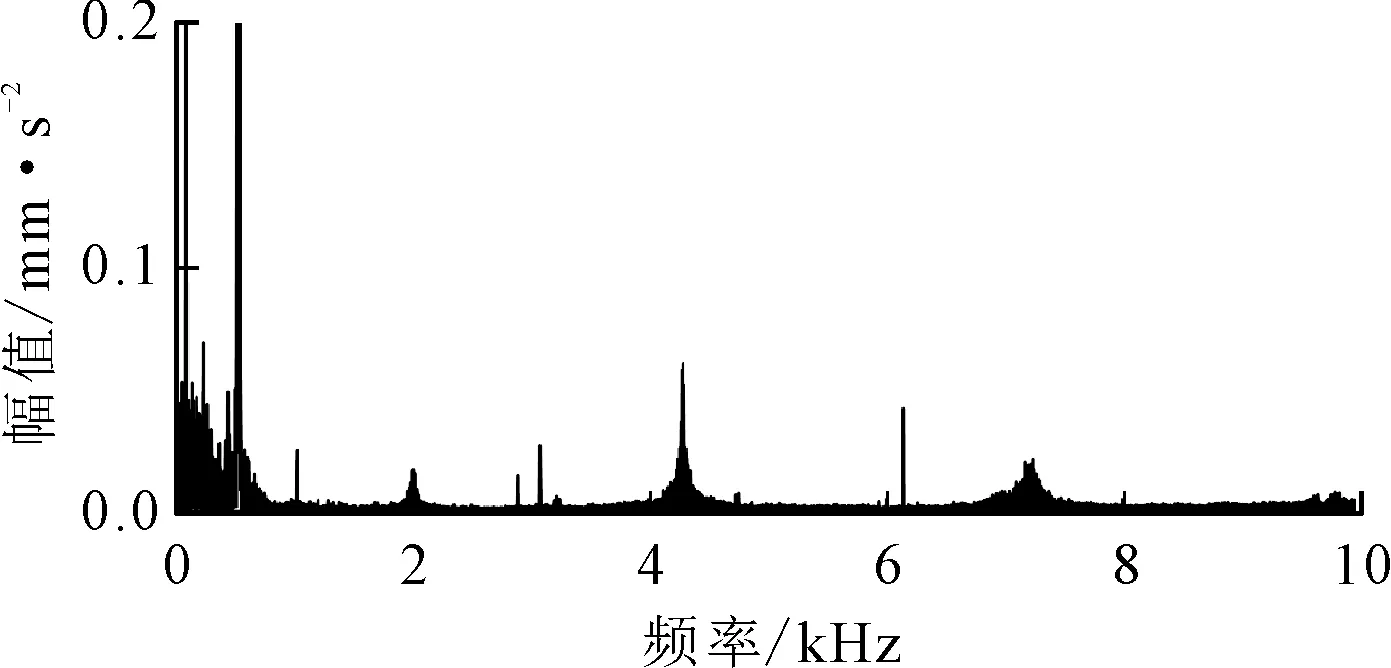
式中:满足tj

由于真实转速和计算转速之间存在误差,在式(7)积分过程中会产生时标误差

(9)

式中:ftrue为Ti时的真实转速;e(Tk)为计算第k个重采样时标时的时标误差。

对上述重采样的角域平稳信号x(a)进行FFT,得到相应阶次谱X(o),采样阶次fo=2π/θ。

(2)频带选择。由于齿轮啮合频带频谱较为复杂,一般齿轮啮合频率及谐波之间难以确定幅值关系,导致直接根据啮合频率的谐波顺序不能确定转频或轴承故障频率调制较为明显的频带,有时存在某中间顺序啮合频率幅值较小甚至接近0的情况。因此,本文主要根据齿轮箱齿数,确定分割频谱的频带中心,再根据轴承型号确定分割频谱带宽,由于一般内圈故障特征系数较大,这里采用内圈故障阶数的4倍作为能量计算宽度

(10)

式中:Ek为啮合阶次第k次谐波的能量;g为与安装传感器的轴直接相连的齿轮箱齿数;b为轴承内圈特征系数;o为计算阶次。

对式(10)计算得到的Ek进行从小到大排序,并取N个能量较大的频带作为后续滤波频带。为了不削弱轴承故障特征成分,且阶次包络平均处理时达到一定的降噪效果,这里N取分割频带个数的一半。

(3)阶次包络平均。针对步骤(2)确定的N个频带确定滤波器参数,对x(a)进行带通滤波,并对滤波后的信号进行Hilbert包络解调处理。其基本原理为通过式(11)进行90°相移,并通过求取原始信号和相移后信号构成解析信号的模,得到原始信号的包络如下

(11)

(12)

对上述包络信号进行FFT变换,得到阶次包络谱,并对N个包络谱平均处理得到最终结果

(13)

3 应用

3.1 实例1

(1)应用描述。为了验证上述机理分析和本文提出方法的有效性,采用某冶金企业粗轧机E2驱动侧的实际工业数据进行验证,该设备测点分布如图3所示。减速箱主要由驱动侧电机、直齿轮、斜齿轮组成,故障轴承为传动侧NU248,该滚动轴承故障阶次如表1所示。采用加速度传感器采集信号,加速度信号的采样频率为20 kHz,转速信号的采样频率为100 Hz。实例1为一块钢的轧制过程,中间阶段为变速变载过程,持续约10 s,与其直接相连的齿轮齿数为25,转速变化趋势先升高再平稳后降低,振动信号及转速信号如图4所示。

图3 E2驱动侧测点分布图

部位外圈内圈滚动体保持架阶次8.24310.7573.7120.434

对比图4的粗轧机原始振动信号和转速波形可以看出,在4 s附近转速提升阶段,振动幅值逐渐升高,表现出较强的非平稳特性。为了验证本文提出方法的有效性,分别取4～6 s非平稳和5～7 s平稳时间段的振动信号进行分析,并和共振解调效果进行对比。

(a)原始振动加速度信号

(b)转速信号图4 粗轧机振动加速度信号及转速波形

图5 4～6 s加速度信号频谱图

(2)非平稳段效果对比。图5为4～6 s信号的频谱图,从频谱图中可以看出存在较大的噪声干扰,且存在较强的频谱混叠,分别在3、4.2、6.5 kHz附近存在3个能量较高的共振峰,相较而言,2 kHz以内中低频段的信号噪声较小,该部分频谱能量主要来源于齿轮。

对截取的上述时间段信号进行谱峭度分析,结果如图6所示,选择的滤波中心频率9 791 Hz处并无明显的共振峰,从共振解调角度并无实际意义。这里选择图5标定的3个共振峰滤波进行对比,滤波频带分别选择2 800～3 300 Hz、4 000～4 500 Hz、6 100～6 600 Hz,同时根据齿轮齿数和轴承内圈故障特征系数确定能带计算范围为了不与共振峰频带有交集,这里取啮合频率的前9次谐波进行能量计算,根据啮合阶次和轴承最大故障阶次确定的频谱区间分割效果见图7。对其按照能量高低进行排序,结果见表2,取能量最大的前5个阶次对角域信号进行带通滤波,图8为3个频带的共振解调结果和本文方法效果的对比。

图6 4～6 s转速非平衡段加速度信号谱峭度

(14)

图7 4～6 s转速非平衡段加速度信号阶次谱

表2 4～6 s各啮合阶次能量

(a)共振频带1包络谱

(b)共振频带2包络谱

(c)共振频带3包络谱

(d)阶次包络平均谱图8 4～6 s转速非平稳段包络谱

图8中fbo、Obo分别为该轴承外圈故障频率及对应阶次,从图中可以看出,本文方法可以较为明显地看到外圈故障的阶次及其谐波,误差约为1.6%。相比之下,3个共振带的包络谱均难以直接找到故障频率成分,且由于转速变化,无法根据频谱中的故障频率确定故障阶次,也即无法准确确定故障类型。因此,本文方法对变速重载状态的齿轮轴承故障具有更好的识别能力。

(3)平稳段效果对比。图9为5～7 s转速平稳时间段信号的频谱图,可以看出,仍存在和图5相似的3个共振峰,且由其谱峭度图10仍不能确定该信号的共振峰位置,取3.2节对应共振峰频带进行滤波解调,与本文方法对比效果如图11所示。

图9 5～7 s转速平稳段加速度信号频谱图

图10 5～7 s转速平稳段加速度信号谱峭度

阶次能量/mm2·s-455～950.064 830～700.089 95～450.133 080～1200.217 2180～2200.220 0105～1450.269 0205～2450.651 7130～1700.803 1155～1951.007 6

(a)共振频带1包络谱

(b)共振频带2包络谱

(c)共振频带3包络谱

(d)阶次包络平均谱图11 5～7 s转速平稳段包络谱

由图9可以看出,尽管旋转机械工作在转速平稳段,经典共振解调方法仍然难以准确找到最优共振峰位置。对比表2和表3可以发现,平稳段与非平稳段轴承故障成分均会对齿轮振动啮合频带进行耦合调制,但能量排序对应的齿轮啮合谐波次序发生了改变,说明了进行能量排序选择频带的必要性。由图11a～11c包络谱可知,共振峰2解调效果较好,但仍存在一定的低频噪声干扰,且仅能看到故障频率1倍频。从本文方法处理效果可以看出,基本消除了所有地毯噪声和低频干扰,且能较为清晰地看到1～3次故障谐波,见图11d。

采用2号共振带的故障频率按照第5 s的转速计算,误差约为0.75%。相比之下,本文方法可以较为准确地找到轴承外圈故障阶次的前3个谐波,且误差约为0.08%,信噪比得到了大幅提升,故障特征提取的准确度明显增加。

3.2 实例2

(1)应用描述。为了进一步验证本文方法的有效性,采用噪声干扰严重、转速较低的精轧机F1分配箱负荷侧的实际工业数据进行实验。该精轧机主要由电机、F1主减速箱、F1分配箱组成,后接轧滚,由于受前端减速箱和后端轧机的影响,振动信号噪声干扰较强。设备测点分布见图12,故障轴承型号为STF2P500,该滚动轴承故障阶次如表4所示,采集信号类型为加速度传感器,采样频率为20 kHz,转速采样频率为100 Hz,整个过程为变速变载过程,振动信号及转速信号如图13所示。