一维非幺正分离时间量子行走的拓扑特性的检测
2019-08-22李洁李志坚
李洁,李志坚
(山西大学 理论物理研究所,山西 太原 030006)
0 引言
近年来,量子行走由于其在基础科学中的重要意义以及一些潜在的应用而受到人们广泛关注。相比于经典随机行走,量子行走因为存在量子相干而具有弹道传输的优势,因此量子行走为量子算法[1]的实现提供了理论依据。近期以来,拓扑特性成为人们关注的热点问题,随着拓扑研究的深入,已经能够在许多物理系统中产生拓扑绝缘体,例如在超导系统[2]、力学系统[3]、光力学系统[4]、光子[5]和原子平台[6]等。分离时间量子行走的能带结构与拓扑绝缘体相似,同时量子行走能隙的大小可以通过演化算符的参数进行调节,因此,分离时间量子行走成为一种较简单的拓扑绝缘体的理论模型为探究物质的拓扑特性提供了有效平台[7]。
近期的研究表明,在分离时间量子行走系统中,可以观测系统的拓扑不变量[8]、量子相变和边界态[9]等。描述量子系统的拓扑不变量主要有绕数[10]、Zak相[11]、陈数等。拓扑相变的突出特征是在不同拓扑相的区域边界处存在拓扑保护边界态[12]。近年来,已经有很多关于分离时间量子行走的拓扑特性的研究,除了超导体和拓扑绝缘体等天然存在的拓扑材料,人们构建了许多人造系统[13]实现量子行走从而研究系统的拓扑特性,但之前的研究大多数是关于厄米系统的幺正性量子行走的研究,本文将通过引入测量算符,实现非厄米系统中的非幺正量子行走[14-16]。我们在实施非幺正量子行走时,将在硬币算符和条件平移算符中各引入一个可控参量,构成二维的参数空间,在此参数空间中研究系统的拓扑相变从而描述系统的拓扑特性,并通过检测相变处拓扑边界态的存在进一步研究非幺正系统的拓扑特性。之后,本文将会探究非幺正分离时间量子行走的平均位移从而获得量子行走的实验可观测量并检验其对抗静态微扰的鲁棒性[17]。
1 非幺正分离时间量子行走及其拓扑不变量
分离时间量子行走定义在位置空间HP和硬币空间HC直积构成的希尔伯特空间H中,由单步时间演化算符U(φ,θ)重复作用于系统初态|Ψ(0)〉实现,即t步演化后系统的状态为
|Ψ(t)〉=Ut(φ,θ)|Ψ(0)〉,
(1)
其中
U(φ,θ)=Sφ(IP⊗Rθ) ,
(2)
IP表示位置空间HP中的单位算符,Rθ为硬币空间Hc中的硬币算符,表示对硬币态的旋转操作,本文选取硬币算符为
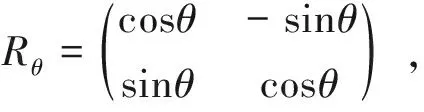
(3)
Sφ为条件平移算符,表示为
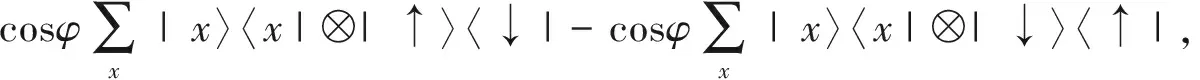
(4)
|x,σ〉=|x〉⊗|σ〉是希尔伯特空间H的基矢。从条件平移(4)式可知,当输入的硬币态不发生翻转时,粒子会以|sinφ|2的概率在一维格点上向左或向右移动,移动的方向由硬币态的方向决定;当粒子硬币态发生翻转时,则会以|cosφ|2的概率静止在原来的位置上保持不变。

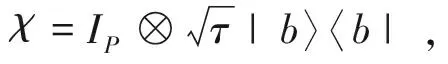
(5)
其中τ表示成功测量到自旋相干态|b〉的概率。若未测量到|b〉态,测量过程的作用由算符
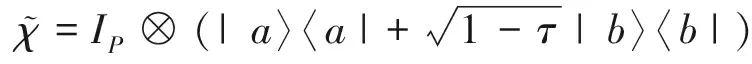
(6)
描述。因此,若第t步测量到自旋相干态|b〉,则量子行走的演化过程为
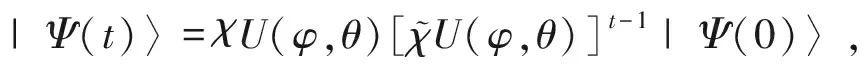
(7)
为了计算方便,我们把幺正算符U(φ,θ)作旋转变换
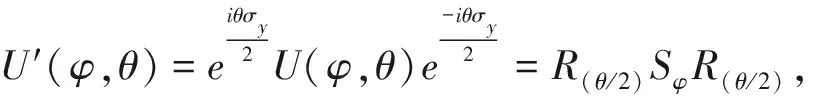
(8)
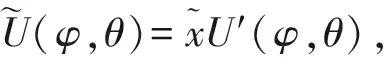
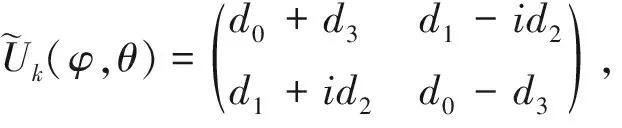
(9)
其中Ic为硬币空间单位矩阵,d0及矢量d={d1,d2,d3}的分量为
d0=pa(sinθcosφ+coskcosθsinφ) ,
(10)
d1=pb(sinθcosφ+coskcosθsinφ) ,
(11)
d2=ipa(cosθcosφ-cosksinθsinφ)+pbsinksinφ,
(12)
d3=ipasinksinφ-pb(cosθcosφ-cosksinθsinφ) ,
(13)
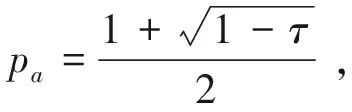
(14)

(15)
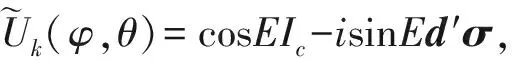
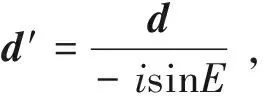
(16)
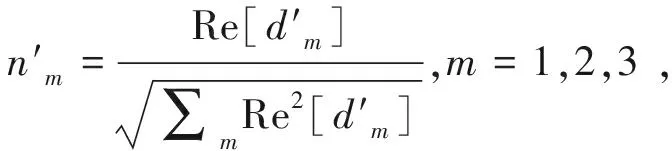
(17)

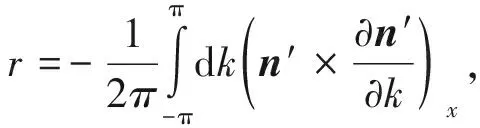
(18)
表示当动量k在第一布里渊区从-π变化到π时,n′在yz平面内绕x轴转动的圈数。
2 非幺正分离时间量子行走的边界态
由体表对应原理[18]可知,在不同的拓扑相区域的边界处会出现边界态。接下来,我们将通过计算非幺正分离时间量子行走在拓扑相边界处的粒子分布概率来探究边界态的存在。由此可以说明利用方程(18)定义非幺正量子行走的拓扑不变量是可行的。

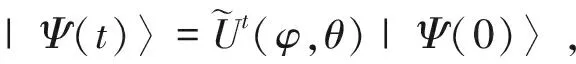
(19)
相应演化t步后在x处测量到粒子的概率为
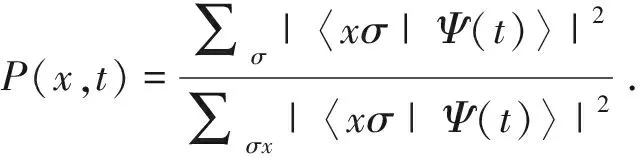
(20)
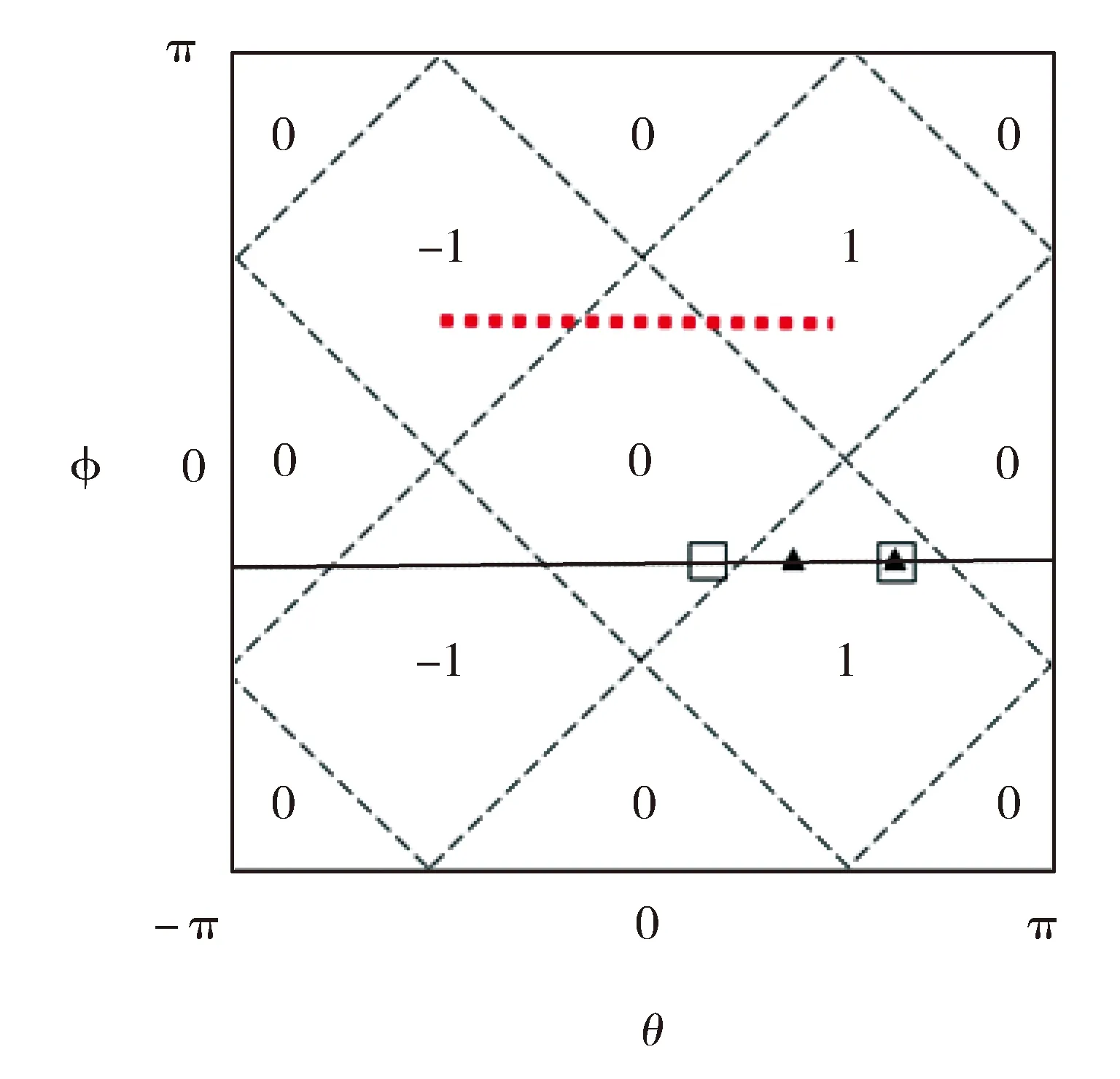
Fig.1 Topological phase diagram in (θ,φ)parameter space for discrete-time quantum walk described by non-unitary operator图1 非幺正算符描述的分离时间量子 行走在参数空间(θ,φ)中的拓扑相图
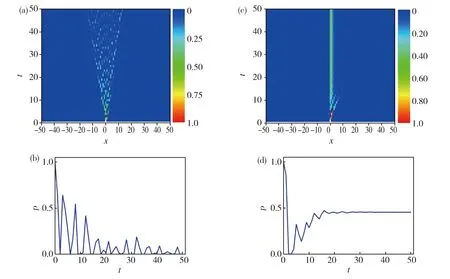
(a)(b)x<0,θ=0.6π and x>0,θ=0.4π,(c)(d)x<0,θ=0.6π and x>0,θ=0.2πFig.2 (a, c)are the changing of probability distribution for non-unitary discrete time quantum walk with t in non-uniform position space;(b, d) are the changing of probability distribution with t at boundary.(a)(b)x<0时θ=0.6π,x>0时θ=0.4π;(c)(d)x<0时θ=0.6π, x>0时θ=0.2π图2 不均匀位置空间中非幺正分离时间量子行走的概率分布随演化步数的变化(a,c)及 量子行走在边界处的概率随时间的变化曲线(b,d)
3 非幺正分离时间量子行走的平均位移及其鲁棒性
在量子系统中,直接检测绕数拓扑不变量是非常困难的,对于幺正量子行走,人们可以通过测量量子行走的平均位移来判断量子行走的拓扑相变[17]。本节中,我们将计算平均位移来描述非幺正分离时间量子行走的拓扑相变。仍然选取非幺正分离时间量子行走的初态为|Ψ(0)〉=|0〉⊗|a〉,若第t步测量到硬币相干态|b〉,则由方程(7)得到此时量子行走的态矢量|Ψ(t)〉,相应地在x位置处检测到量子行走处于硬币态|b〉的概率为
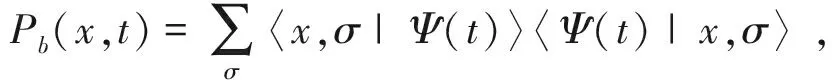
(21)
重复多次量子行走过程,并对硬币相干态|b〉进行测量,则多次测量后的量子行走的平均位移为
(22)
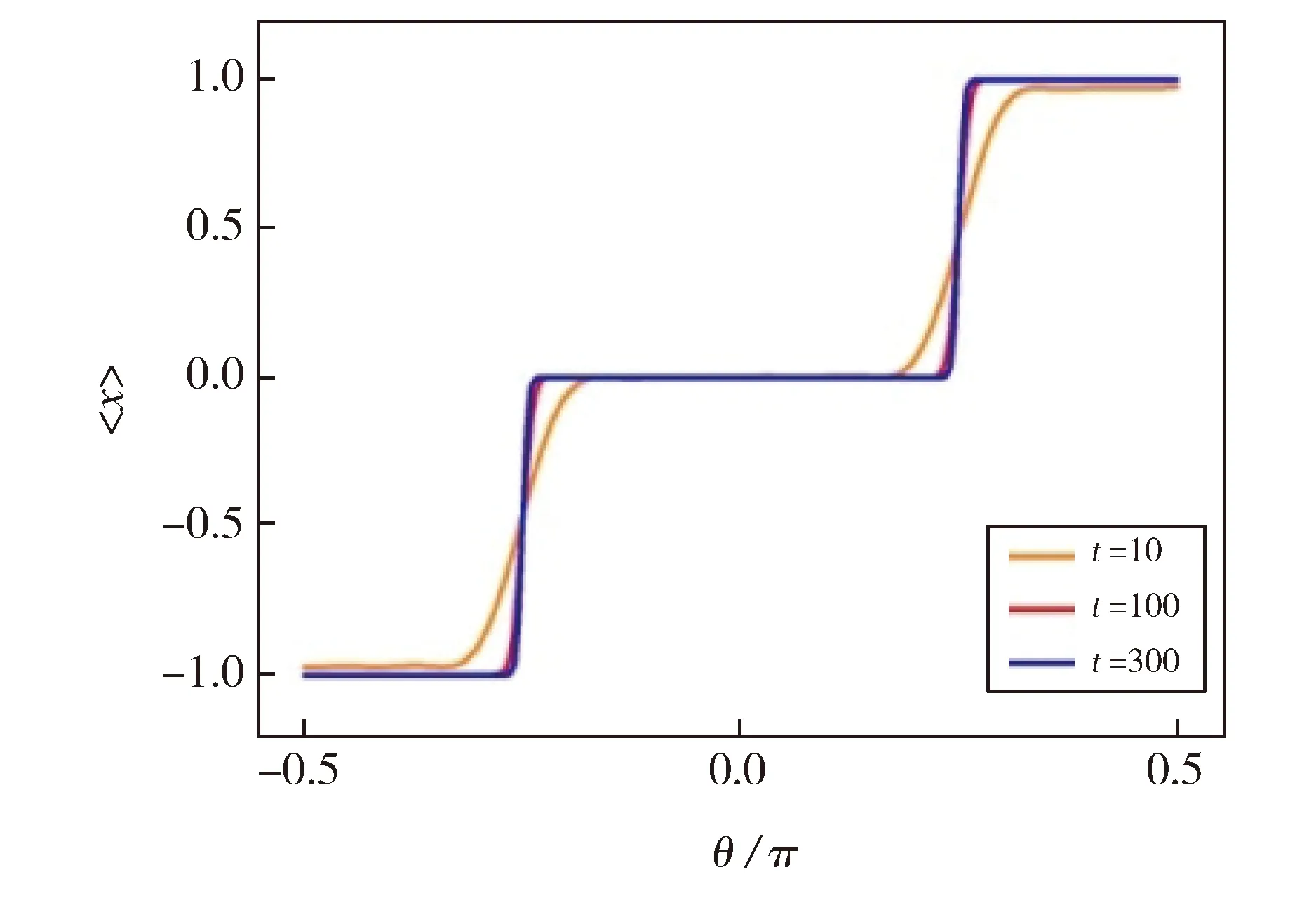
Orange, red and blue solid are correspond to the measurement processes for t=10, 100, and 300Fig.3 Changing for average displacements of non-unitary discrete time quantum walk with the coin parameter θ橙色、红色和蓝色线分别对应t=10、100、300次的测量过程图3 非幺正分离时间量子行走的平均位移 随硬币参数θ的变化曲线
图3给出量子行走的平均位移随硬币参数θ的变化图,其中取参数φ=π/4,τ=0.5,橙色、红色和蓝色线分别对应t=10、100、300次的测量过程。由图中可知,随着测量过程的增加,平均位移随相变参数θ的变化出现更明显的台阶跳跃变化,与图1中红色点线的参数取值对比,平均位移跳变时对应的θ取值正好是不同拓扑结构的相边界。在相同拓扑绕数的参数区域,平均位移保持常数不变。因此可以通过可测的平均位移来刻画非幺正量子行走的拓扑相变。
如果通过参数φ对非幺正量子行走引入静态微扰Δ,即令φ=π/4+Δ,Δ在[-π/20,π/20]的范围内随机的取值。在相同静态微扰下,重复10次量子行走过程,并在不同步演化过程中对硬币相干态|b〉进行测量,计算得到平均位移〈x〉,然后重复选取4 000次随机数Δ,并计算平均位移的平均值,得到其随参数θ的变化曲线,如图4蓝色实线所示。与不加微扰时的红色虚线相比,基本没发生改变,说明非幺正分离时间量子行走的平均位移具有鲁棒性,是拓扑保护的结果。

The red dashed line is the non-unitary discrete time quantum without dynamical perturbation when the average displacement changes with the coin parameter,τ=0.5,φ=π/4+Δ,Δ is the static perturbation introduced by the parameter φ,the blue solid line is the average displacement as a function of coin parameters in the presence of static perturbation Fig.4 Average displacement for non-unitary discrete-time quantum walk is a function of coin parameter under static perturbation.红色虚线为没有静态微扰时平均位移随硬币参数的变化曲线,τ=0.5, φ=π/4+Δ,Δ是由参数φ引入的静态微扰,蓝色实线为存在静态微扰时平均位移随硬币参数变化的曲线图图4 无序静态微扰下,非幺正分离时间量子行走的平均位移随硬币参数θ的变化曲线
4 结论
本文通过引入部分测量算符将幺正分离时间量子行走推广至非幺正的情况,给出非幺正量子行走的拓扑相图。进而引进空间不均匀的非幺正分离时间量子行走,发现在拓扑数不相同的边界上,量子行走的分布概率随演化时间的增加趋于一常数值,说明在边界上存在拓扑保护的边界态,而当空间不均匀的边界两侧的拓扑数相同时,则边界上的分布概率会趋于0,不存在边界态。最后计算量子行走的平均位移,及其受静态微扰影响的情况,说明利用平均位移随相变参数的变化可以表征量子行走拓扑相变。
