速度匹配加机动辅助的滚转弹滚转角空中对准法

2019-08-22彭博岑梦希

兵工学报 2019年7期

彭博，岑梦希

(中国航天空气动力技术研究院彩虹无人机科技有限公司，北京 100074)

0 引言

滚转弹具有伺服、制导控制系统简单，武器系统可靠性高、成本低等特点。越来越多的小型战术武器开始采用滚转体制[1]，为实现对目标的精确打击，如何对滚转姿态进行高精度地辨识已成为研究热点。火控系统通常能够完成滚转弹导航参数的粗对准，但由于滚转弹自身的高动态特性，导致惯性测量单元(IMU)工作在恶劣环境下，解算的滚转角误差逐渐积累，滚转角解算精度不足，进而影响控制系统的正常工作。因此，仅采用弹上IMU解算滚转角是不够的，还需具备在空中进行滚转姿态校正、精对准的能力。

采用地磁传感器并通过一定算法能够获取弹体姿态信息[2-4]，但地磁易受干扰，系统可靠性相对较低。采用低成本的捷联激光探测器与全球定位系统(GPS)组合也能够对滚转角进行测量[5]，但姿态角用弹道角近似，仅适用于全弹道攻角较小的修正弹一类武器。另外，采用卫星与惯性组合方案可对滚转角进行一定程度的辨识，佘浩平等[6]提出了一种基于制导弹药的简易滚转角对准方法，该方法计算量小，工程上易于实现，但由于姿态角同样用弹道角近似，且由于没有考虑状态误差，仅采用考虑观测误差的最小二乘法，滚转角的对准误差较大。Wu等[7-8]提出了一种采用卫星辅助的姿态对准方法，可实现对飞机的姿态校正及对准，但还未在滚转弹领域得到应用。

采用卫星与惯性组合速度匹配方案对姿态进行估计已经相对成熟[9-11]，但由于该方法不具备在空中对姿态进行观测的能力，对于高动态的滚转弹，姿态角的估计、对准精度较低。本文在采用卫星惯性速度匹配模式的基础上，辅以设计的比例导引加重力补偿纵向机动策略，结合卡尔曼滤波技术，同时考虑状态和量测误差，在保证制导回路闭合的基础上，实现对滚转角的空中校正、精对准。

与如今较为成熟的对准算法相比：该方法在推导过程中采用实际的姿态角，而不是用弹道角近似，准确度更高；通过卡尔曼滤波融合了状态与量测的误差特性；无需增加其他传感器(地磁，捷联探测器)等，增加了系统的可靠性。

1 速度匹配法模型建立

1.1 状态方程

粗对准过程结束后，姿态误差角一般较小，可以采用捷联惯性导航姿态、速度误差线性模型作为基础，有

(1)

将误差方程建立在准机体坐标系nb下，定义nb坐标系x轴指向载体右侧，y轴指向前，z轴指向上，有

(2)

设弹体所受比力fnb=[fxfyfz]T，代入(2)式并展开，有

(3)

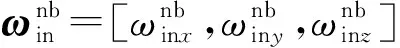
(4)

式中：误差状态

(5)

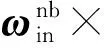
(6)

1.2 观测方程

如1.1节所述，状态方程是以误差模型建立的，故观测方程也以观测量的差值进行构建。本文采用速度匹配法，即在卫星与惯性组合模式下，将二者输出的速度做差处理，转换至准机体坐标系作为观测量。设卫星测量的速度为

(7)

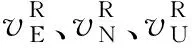
(8)

式中：δvE、δvN、δvU为惯性解算速度误差在导航坐标系下的分量。将(7)式与(8)式作差运算，并转换至nb坐标系，建立基于速度匹配法的空中姿态精对准观测方程，有

(9)

式中：观测矩阵

H=[I3×303×303×6]；

(10)

噪声向量V表示卫星测速噪声在机体坐标系中的分量。

至此，完成了速度匹配法对准模型的建立，从(3)式可以看出，姿态误差角的存在会产生速度误差，通过(9)式，综合卫星与惯性系统的速度输出，将速度误差转换到准机体坐标系后可通过卡尔曼滤波算法对姿态误差角进行一定估计，进而对姿态角进行校正与对准，卡尔曼滤波算法的基本过程本文不再赘述。

2 速度匹配加机动辅助法

2.1 可观测性分析

由于卫星与惯性组合系统无法量测弹体姿态角，当采用卡尔曼滤波算法进行姿态误差估计时，只能通过组合系统输出的速度误差间接对其进行估计，估计精度受限于其他不可观测量(如传感器漂移)[12]。下面对速度匹配模型的可观测性进行分析。

滚转弹飞行过程中，状态方程是时变的，观测方程保持不变。根据分段式定常系统理论[13-14]，可将时变系统作分段定常处理并进行可观测性分析，运用满秩变换技术[15-16]将速度匹配对准模型进行线性变换，令

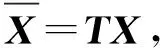
(11)

式中：

(12)

(13)

(14)

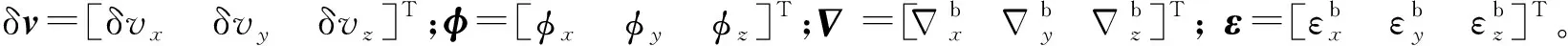
(15)

式中：

(16)

2.2 机动辅助法

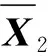
(17)

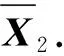
在滚转弹的无控段，弹体轴向阻力加速度fy与fz、fx相比一般较大，由于弹体滚转，fysinγ和fycosγ呈正交变化，故俯仰误差角φx和航向误差角φz均可被估计出来，进而可对俯仰角和航向角进行校正。

假设无控段弹体轴向加速度计零偏为0.05g，滚转弹初始俯仰角误差、航向角误差以及滚转角误差均为5°. 图1为轴向加速度计零偏的估计曲线，图2为校正后的姿态角误差曲线。

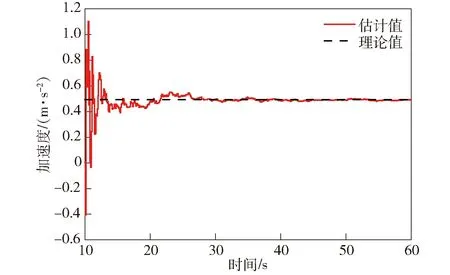
图1 轴向加速度计零偏估计Fig.1 Zero bias of axial accelerometer

图2 姿态角误差Fig.2 Attitude angle errors

由图1和图2中可以得知：在无控段，轴向加速度计零偏可以被估计出来；俯仰角、航向角误差逐渐收敛，俯仰角、航向角估计、对准精度较好；滚转角误差基本不收敛，滚转角估计、对准精度差。

相比于俯仰角和航向角，滚转角对于滚转弹的控制系统设计更为重要，为了能够估计出滚转误差角，根据(17)式，需要适当增加φy的系数，即增大fxsinγ+fzcosγ或者fxcosγ-fzsinγ. 故可通过增加纵向机动fz或者增加侧向机动fx来提高φy的估计精度。

3 机动辅助策略

对于采用卫星与惯性组合系统的滚转弹，可以采用卫星与惯性组合制导方式，利用组合导航信息进行制导信息的提取，假设目标静止，在已知目标位置以及滚转弹速度、位置的情况下，纵向视线角速度为

(18)

侧向视线角速度为

(19)

式中：vx、vy、vz为弹速在地面坐标系x轴、y轴、z轴3个分量；xMT、yMT、zMT分别为弹目相对位置在地面坐标系x轴、y轴、z轴3个分量。这些量可通过组合导航系统获取得到。

因此，当滚转弹完成粗对准后，在卫星与惯性组合提供的制导信息下，可以提前进入制导阶段，制导指令驱动自动驾驶仪控制舵机，弹体通过过载响应产生纵向、侧向机动。相比于纵向视线角速度，侧向视线角速度较小，故侧向机动效果较弱。本文忽略风速和侧向拉偏，考虑纵向平面内，采用比例导引加重力补偿制导方式驱动弹体纵向机动的生成，实现纵向机动辅助策略。纵向比例导引加重力补偿制导律形式为

(20)

式中：ny为纵向机动指令，来驱动滚转弹产生纵向机动，进而提高φy的估计精度，实现滚转角空中对准；N为导航比；v为导弹速度；Kg为重力补偿系数；g为重力加速度；θ为弹道倾角。

根据(20)式，调节导航比N的取值可以改变纵向机动指令，来实现弹体纵向机动fz大小的控制，为了不影响制导精度，N取值在2～6之间。

根据(20)式，调节重力补偿系数Kg的取值也可以改变纵向机动指令，来实现弹体纵向机动fz大小的控制。同样，为了不影响制导精度，Kg取值选在1～2之间。

4 仿真校验

假设在滚转弹发射后30 s时开始采用速度匹配加机动辅助法进行滚转姿态精对准，IMU输出频率为1 000 Hz，卫星导航系统输出频率为10 Hz，假设IMU中的加速度计存在常值偏差0.05g，随机漂移0.01g，陀螺仪存在常值偏差0.1°/s，随机漂移0.05°/s；假设卫星导航系统的测速误差为0.5 m/s. 某炮射滚转弹在速度200 m/s下的名义转速为5 r/s，忽略马格努斯和陀螺效应，设定弹体初始速度800 m/s，初始俯仰角45°，航向角45°，滚转角0°，目标坐标(25 000 m,0 m,0 m)，采用卫星与惯性组合制导体制，制导开始时间为40 s，机动辅助法采用比例导引加重力补偿的纵向机动辅助策略。

4.1 不同导航比对滚转角对准的影响

仿真条件假设经过粗对准后的初始滚转角误差分别为10°和-10°，同时考虑俯仰角、航向角初始误差及速度初始误差，根据图2可知，无控段的俯仰、航向角误差较小，故仿真设定俯仰角、航向角误差均为2°，东向、北向、天向速度初始误差均取2 m/s，通过调节导航比来控制弹体纵向机动fz的大小，选取导航比N分别为2.5、3.5、4.5 3种情况进行仿真分析，重力补偿系数Kg取1.5，不同导航比下的滚转角对准误差曲线如图3和图4所示。

图3 初始滚转角误差10°时的滚转角误差Fig.3 Roll angle errors with initial error of 10°

图4 初始滚转角误差-10°时的滚转角误差Fig.4 Roll angle errors with initial error of -10°

导航比的变化直接影响弹体纵向机动响应，不同导航比下的纵向机动如图5所示。

图5 纵向加速度对比Fig.5 Comparison of longitudinal accelerations

由图3～图5可知：30～40 s为粗对准后- 制导前阶段，此阶段内弹体无纵向机动，滚转角误差不收敛；40 s后开始制导，采用比例导引加重力补偿纵向机动辅助法，3种导航比下滚转角误差均收敛至2°以内，收敛时间小于10 s，稳态精度差别较小；而不采用机动辅助的卫星与惯性速度匹配法，滚转角误差持续发散，无法完成对准。故机动辅助法对滚转角的空中对准效果较好，且能够在全弹道(飞行时间90 s)范围内保持对准精度；在重力补偿系数一定的情况下，在此弹道条件下，导航比减小，纵向机动增加；当导航比从4.5调节到2.5时，纵向加速度只变化了15%，对准速度增加0.1～0.2 s，对准精度相差很小，故对准速度、精度对导航比的变化敏感度不高。

分析滚转角的对准误差对俯仰角、航向角误差的影响，不同导航比下的俯仰角误差曲线如图6和图7所示，航向角误差曲线如图8和图9所示。

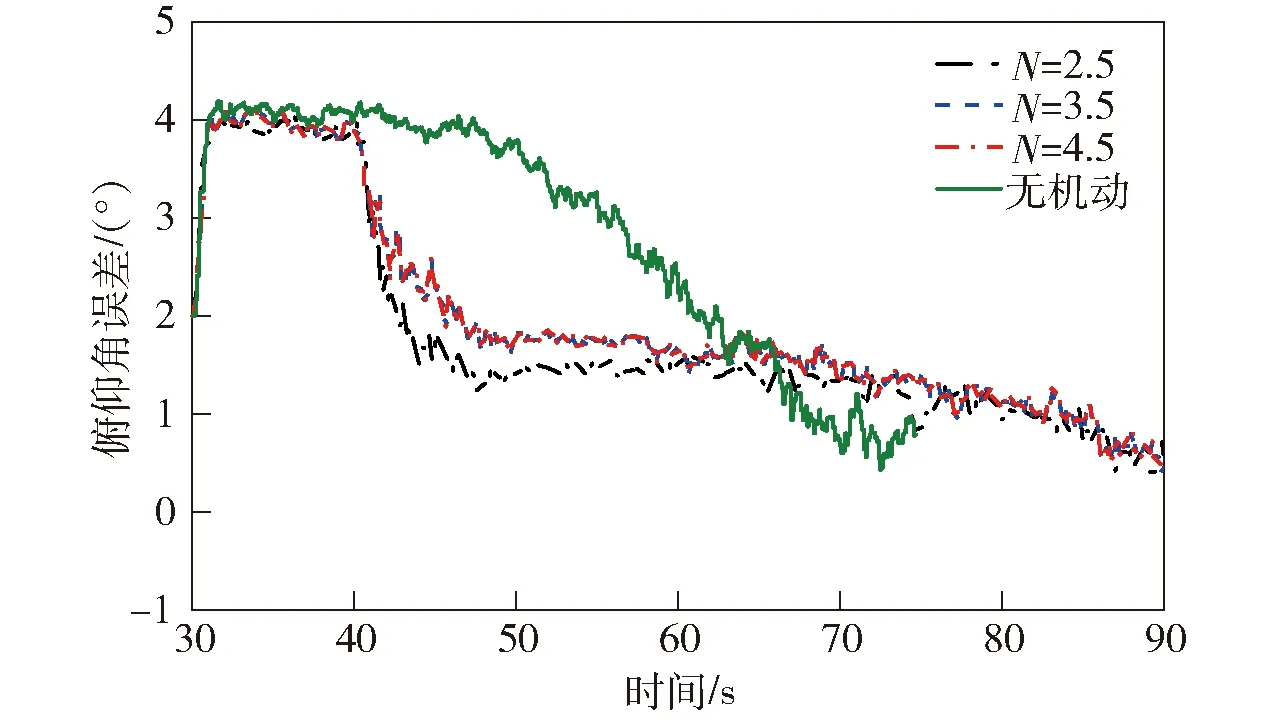
图6 初始滚转角误差10°时的俯仰角误差Fig.6 Pitch angle errors with initial error of 10°

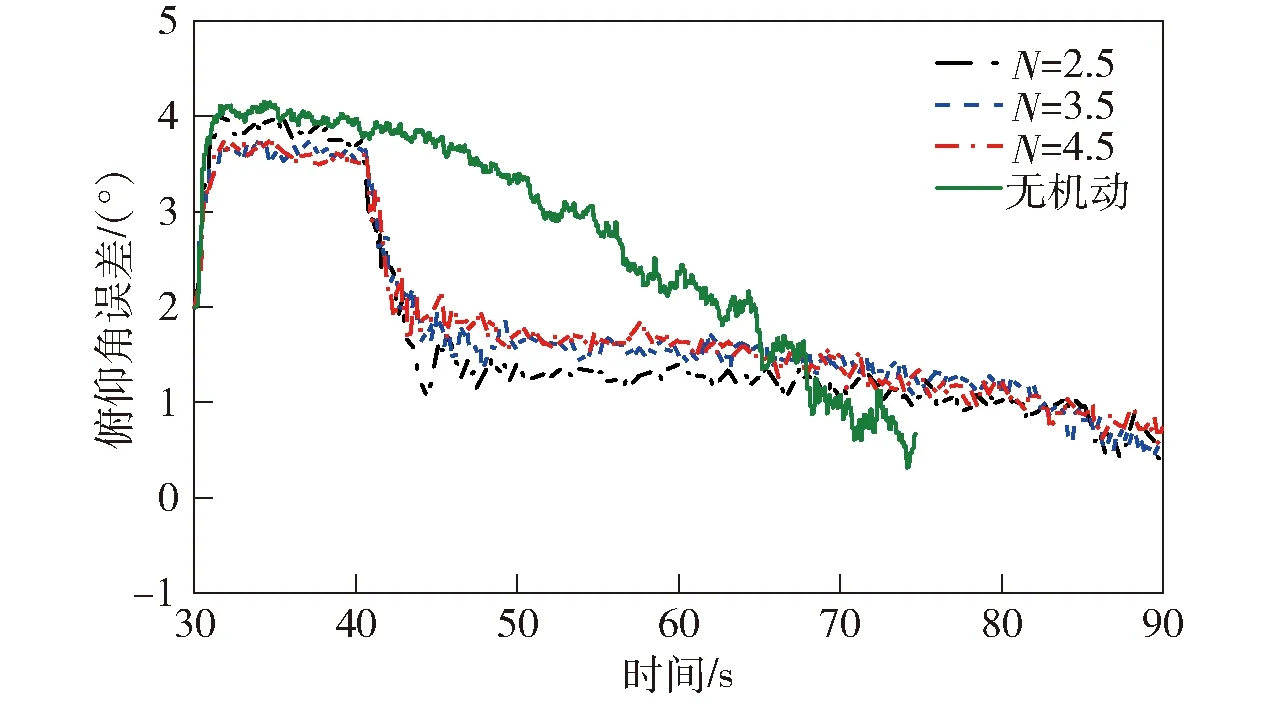
图7 初始滚转角误差-10°时的俯仰角误差Fig.7 Pitch angle errors with initial error of -10°

图8 初始滚转角误差10°时的航向角误差Fig.8 Course angle errors with initial error of 10°

图9 初始滚转角误差-10°时的航向角误差Fig.9 Course angle errors with initial error of -10°

由图6～图9可以得知：40 s之前比例导引加重力补偿纵向机动辅助法未作用时，滚转角对准误差较大，俯仰、航向角误差因受其影响而不收敛；当纵向机动辅助法作用时，3种导航比下俯仰、航向角误差均呈收敛趋势，俯仰角误差可控制在2°以内，航向角误差可控制在5°以内，这是由于对滚转角的精确辨识可抑制俯仰角、航向角误差的发散；而不采用机动辅助的卫星与惯性速度匹配法，俯仰角、航向角误差收敛性较差，甚至发散。

分析滚转角的对准误差对速度误差的影响，取滚转角初始误差为10°，不同导航比下的东向、北向、天向3个方向的速度误差如图10～图12所示。

图10 东向速度误差Fig.10 Errors of vE

图11 北向速度误差Fig.11 Errors of vN

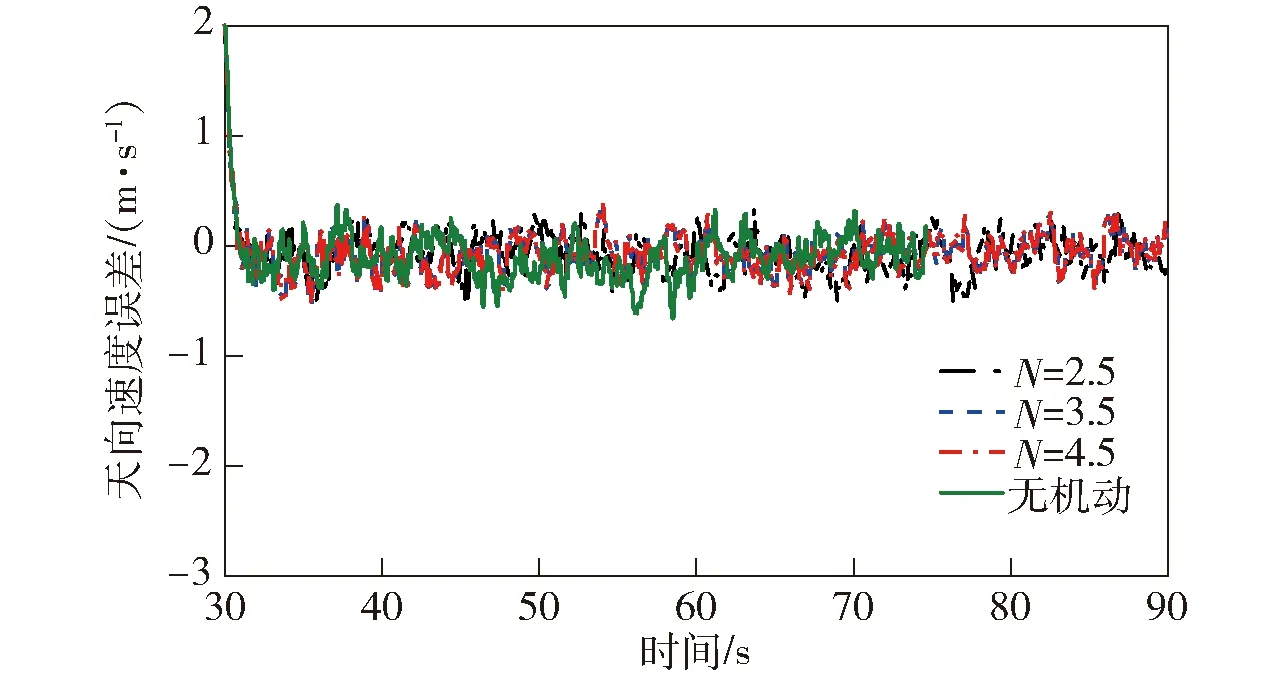
图12 天向速度误差Fig.12 Errors of vU

由图10～图12可以得知，无论是否采用纵向机动辅助法，3个方向的速度误差均收敛在0.5 m/s以内，这是因为在速度匹配法中，速度是直接观测量，可通过卡尔曼滤波直接对其进行校正。因此，初始姿态误差、是否采用纵向机动辅助都不影响速度误差的收敛。纵向机动辅助法只对姿态角误差有影响，故后文不再对速度误差进行分析。

进一步分析不同导航比下的弹道特性，3种导航比下的纵向弹道如图13所示。

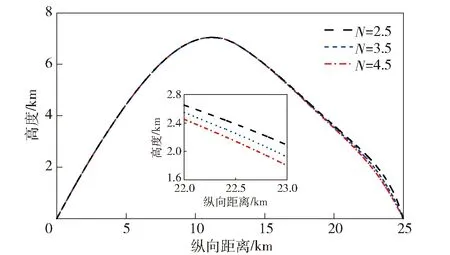
图13 纵向弹道对比Fig.13 Comparison of longitudinal trajectories

由图13可以得知：在重力补偿系数一定的情况下，减小导航比，弹道略微上抬，影响效果不明显，末端均可以命中目标；通过调节导航比实现纵向机动辅助的策略在完成滚转角精对准的同时，不影响制导精度。导航比主要起到闭合制导回路，保证制导精度的作用，对滚转角的对准特性影响不大。

4.2 不同重力补偿系数对滚转角对准的影响

进一步研究不同重力补偿系数对滚转角对准的影响，仿真条件仍假设经过粗对准后的初始滚转角误差分别为10°和-10°，通过调节重力补偿系数来控制弹体纵向机动fz的大小，选取重力补偿系数Kg分别为1.0、1.2、1.5 3种情况进行仿真分析，导航比N取3.5，不同重力补偿系数下的滚转角对准误差曲线如图14和图15所示。

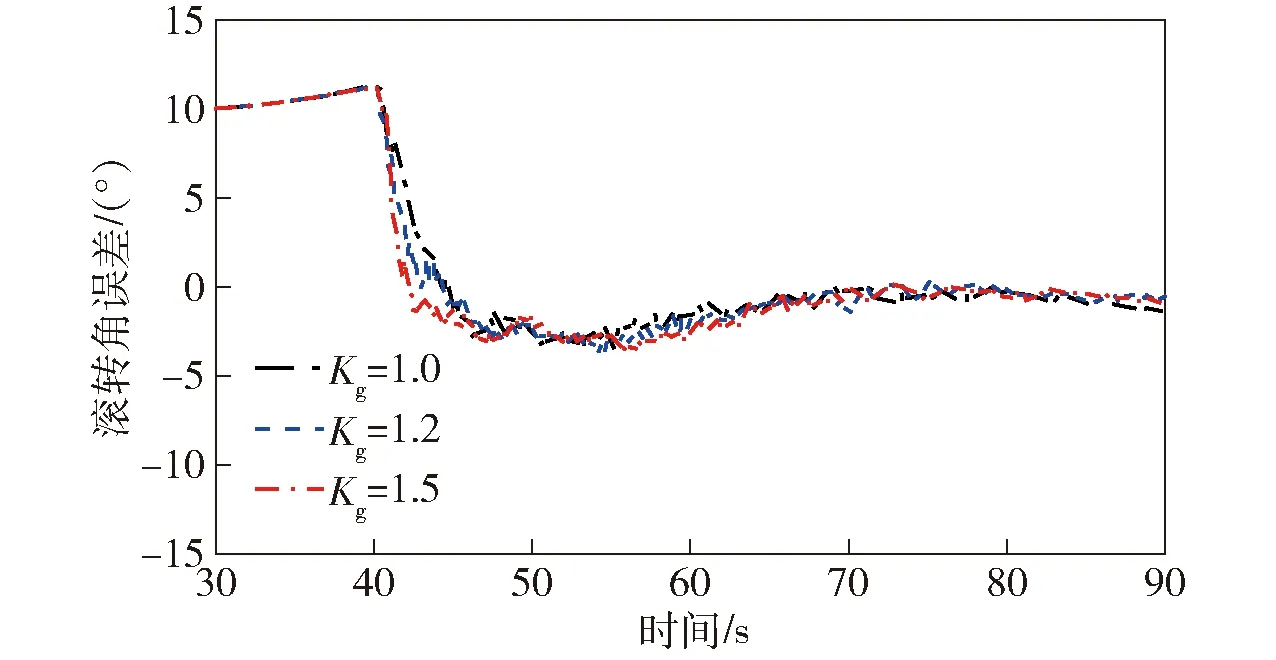
图14 初始滚转角误差10°时的滚转角误差Fig.14 Roll angle errors with initial error of 10°

图15 初始滚转角误差-10°时的滚转角误差Fig.15 Roll angle errors with initial error of -10°

重力补偿系数的变化直接影响弹体纵向机动响应，不同重力补偿系数下的纵向机动如图16所示。

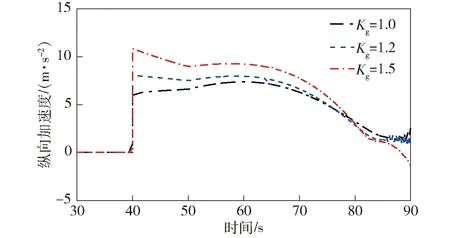
图16 纵向加速度对比Fig.16 Comparison of longitudinal accelerations

由图14～图16可以得知：采用比例导引加重力补偿纵向机动辅助法，3种重力补偿系数下滚转角误差均收敛至2°以内，收敛时间小于10 s，且能够在全弹道(飞行时间90 s)范围内保持对准精度；在导航比一定的情况下，在此弹道条件下，重力补偿系数增大，纵向机动增加；重力补偿系数从1.0调节到1.5时，纵向加速度变化了74%，误差收敛时间减少3～4 s，稳态误差均值由1.1°降至0.9°. 因此，可通过增大重力补偿系数来提高对准速度以及精度。相比于改变导航比，改变重力补偿系数可以更有效地改善滚转角对准特性。

分析滚转角的对准误差对俯仰角、航向角误差的影响，不同重力补偿系数下的俯仰角误差曲线如图17和图18所示，航向角误差曲线如图19和图20所示。

图17 初始滚转角误差10°时的俯仰角误差Fig.17 Pitch angle errors with initial error of 10°

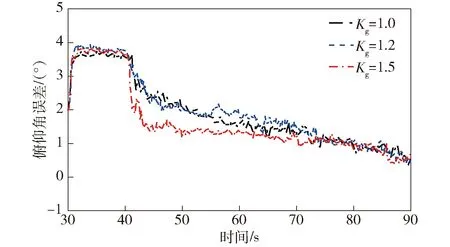
图18 初始滚转角误差-10°时的俯仰角误差Fig.18 Pitch angle errors with initial error of -10°

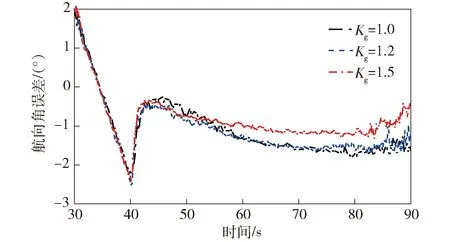
图19 初始滚转角误差10°时的航向角误差Fig.19 Course angle errors with initial error of 10°

图20 初始滚转角误差-10°时的航向角误差Fig.20 Course angle errors with initial error of -10°

由图17～图20可以得知，纵向机动辅助法未作用时，滚转角对准误差较大，俯仰角、航向角误差因受其影响而不收敛；当纵向机动辅助法作用时，3种重力补偿系数下俯仰角、航向角误差均呈收敛趋势，与4.1节所得结论相同。故可得：纵向机动辅助法在完成滚转角对准的同时，可保证俯仰角、航向角误差收敛。

进一步分析不同重力补偿系数下的弹道特性，3种重力补偿系数下的纵向弹道如图21所示。

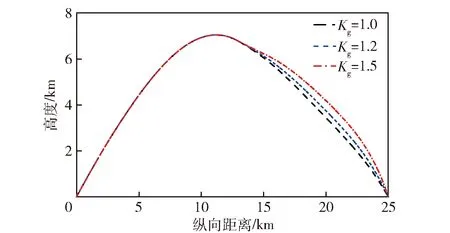
图21 纵向弹道对比Fig.21 Comparison of longitudinal trajectories

由图21可以得知：在导航比一定的情况下，重力补偿系数由1.0变化至1.5的过程中，弹道出现拉高上抬趋势，但末端均可以命中目标；故通过调节重力补偿系数实现纵向机动辅助的策略在完成滚转角精对准的同时，可保证一定的制导精度。

纵向机动随着重力补偿系数增加而增大，但过大的重力补偿系数将导致滚转弹落地精度的损失，为了保证制导精度，需要限定重力补偿系数的范围。在上述给定的仿真条件下，选取9组重力补偿系数(范围1.0～3.0)，对采用不同重力补偿系数的纵向机动辅助法进行蒙特卡洛弹道仿真，每种工况的仿真次数为1 000，用脱靶量的平均值表征制导精度，不同重力补偿系数下的脱靶量平均值如图22所示。

图22 不同重力补偿系数下的脱靶量平均值Fig.22 Average miss distances under different Kg

由图22可以得知：当重力补偿系数在1.0～2.0之间时，脱靶量始终维持在2 m以内；当重力补偿系数增加至2.0以上时，脱靶量开始有增大趋势；当重力补偿系数增加至2.5以上时，脱靶量将迅速发散，重力补偿系数越大，脱靶量越大，落地精度越低。因此，比例导引加重力补偿纵向机动辅助法需要对重力补偿系数进行一定约束，其取值范围在1.0～2.0之间，为了增加滚转角的对准速度及精度，重力补偿系数可以取在1.5～2.0之间。

综合4.1节及4.2节的仿真结果及分析，可以得出：采用比例导引加重力补偿纵向机动辅助策略，相比于卫星与惯性速度匹配法，滚转角对准效果更好；在一定范围内(1.0～2.0)内改变重力补偿系数对滚转角对准特性的改善优于改变导航比，导航比主要对制导回路起到闭合作用。纵向机动辅助策略可完成滚转角的精对准，同时保证制导精度。

为了验证比例导引加重力补偿纵向机动辅助策略的抗干扰性，对该算法进行拉偏仿真分析。

4.3 转速拉偏对机动辅助策略的影响

在4.1节和4.2节的仿真验证中，滚转弹的名义转速为5 r/s，为了验证纵向机动策略对不同转速具有适应性，进一步将名义转速拉偏，导航比N取3.5，重力补偿系数Kg取1.5.

设某炮射滚转弹的初始诸元不变，仿真条件仍假设初始滚转角误差分别为10°和-10°，名义转速范围为5 ～ 15 r/s，转速曲线如图23所示。

图23 转速Fig.23 Rotating speed

图24 滚转角误差Fig.24 Roll angle errors

转速拉偏条件下的滚转角对准误差曲线如图24所示。转速拉偏条件下的俯仰、航向角误差曲线分别如图25和图26所示。

图25 俯仰角误差Fig.25 Pitch angle errors

图26 航向角误差Fig.26 Course angle errors

由图24～图26得知：名义转速在5～15 r/s变化时，比例导引加重力补偿纵向机动辅助策略可保持对滚转角的精对准能力，对准精度在2°以内，收敛时间在15～20 s左右；并且可保证俯仰、航向角误差收敛，验证了该策略对转速拉偏具有一定的抗干扰性。

4.4 惯性传感器误差对机动辅助策略的影响

在工程应用中，随着滚转弹飞行状态、工作环境的改变(如过载、温度、压强等)，惯性微机电系统(MEMS)的常值偏差与随机漂移等误差与射前标定值会产生一定偏差，而卡尔曼滤波器的参数此时已固化在软件中。为模拟真实工作中滤波器参数不变，惯性传感器误差改变对滚转角空中对准产生的影响，将传感器误差进行拉偏，卡尔曼滤波器参数、卫星定速误差以及发射诸元均不改变，导航比N取3.5，重力补偿系数Kg取1.5，名义转速取5 r/s，采用该策略进行精对准仿真。惯性传感器误差拉偏参数如表1所示。

表1 传感器测量误差工况

传感器测量误差拉偏条件下的滚转角对准误差如图27和图28所示。

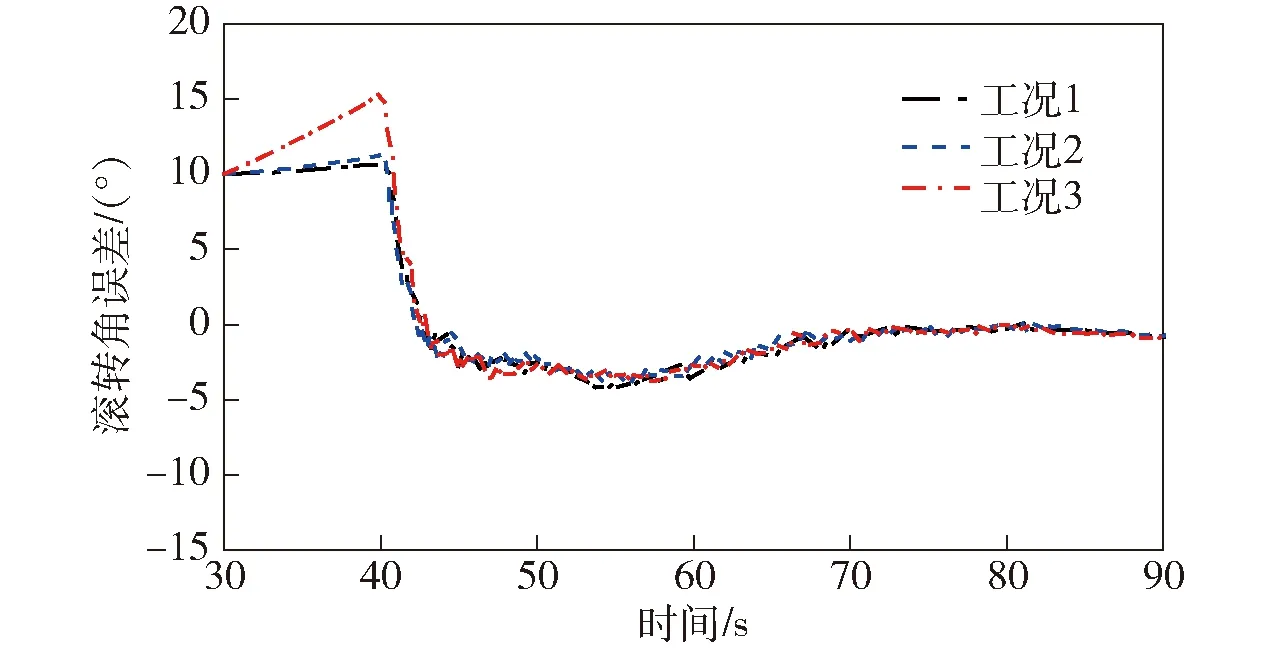
图27 初始滚转角误差10°时的滚转角误差Fig.27 Roll angle errors with initial error of 10°

选取的工况3测量误差较大，基本可以代表低成本、低精度MEMS的量测特性。由图27和图28可知，在滤波器参数固化的情况下，惯性传感器测量误差改变时，比例导引加重力补偿纵向机动辅助策略可保持对滚转角的精对准能力，对准精度在2°以内，收敛时间在10～15 s左右，验证了该策略对惯性传感器误差具有一定的抗干扰性。