基于滤波器组的船舶静电场跟踪

颜冰， 孙宝全,2， 张伽伟

(1.海军工程大学 兵器工程学院， 湖北 武汉 430033； 2.92941部队， 辽宁 葫芦岛 125000)

0 引言

船舶静态电场(SE)是船舶重要的信号源，目前相关学者对船舶电场建模已经作了大量的研究，且有比较成熟的结论。根据船舶的电场模型，从船舶SE信号中可以反演出船舶的位置信息，可以用来对船舶进行跟踪定位[1-2]。相比于水声信号，电场信号所受环境影响相对较小。利用船舶静电场对船舶目标进行跟踪定位可以作为水声跟踪定位的一个有效补充。利用船舶静电场对目标船舶进行跟踪主要应用在水雷、水下预警系统中，由于此类装备对功耗和计算资源有较高的要求，为此对滤波算法的复杂度也提出了较高的要求。相比于粒子滤波，卡尔曼滤波计算方法简单，计算量小，更利于在水下武器中的工程化实现。以卡尔曼滤波为代表的滤波算法可以根据传感器量测信息对目标的相关参数进行实时的估计，在目标跟踪领域获得越来越广泛的应用[3]。

与传统的雷达跟踪应用不同，在船舶静电场跟踪中，其方位- 距离信息隐含于观测信号之中，滤波跟踪算法的先验信息是缺失的[4]。在非线性条件下，现有的滤波算法中不论是分布近似方法(粒子滤波类)还是矩近似方法(卡尔曼滤波类)均不能保证任意初值条件下的滤波收敛性，根本原因在于参与滤波更新的量是根据当前一步预测状态，因此初值与真实值之间相差过大会导致滤波发散。解决先验信息缺失常用的方法是滤波器组[5-6]法，即采用一组滤波器，假设多个可能的初值，然后用一定的方法选择出最优结果。

本文将以渐进更新扩展卡尔曼滤波器(PUEKF)为最基本的滤波单元，引入基于最大似然选择的滤波器组方法，解决船舶静电场跟踪中先验信息缺失的问题。

1 船舶SE跟踪问题描述

船舶SE跟踪问题的状态空间模型[7]为

(1)

式中：xk为k时刻的n维状态向量，xk∈n；yk为k时刻m维观测向量,yk∈m；a为状态转移函数，a:n→n；h为观测函数,h:n→m；wk-1为状态噪声向量，wk-1∈n，vk为观测噪声向量，vk∈m且wk-1～N(0,Qk-1)、vk～N(0,Rk)，Qk-1为过程噪声协方差矩阵，Rk为观测噪声协方差矩阵，{wk-1}和{vk}不相关。

1.1 观测方程

采用水平电偶极子对船舶电场进行建模；在空气- 海水- 海床3层均匀介质条件下，任意场点Pf处的电场信号[8]为

E=(Ex,Ey,Ez)，

(2)

式中：Ex、Ey、Ez分别为

x、y、z为场点坐标，x0、y0、z0为场源位置坐标，px、py、pz分别为电偶极子电偶极矩p在3个坐标轴上的分量值，η为海床反射系数，η=(σs-σsb)/(σs+σsb)，σs为海水电导率，σsb为海床电导率，D为海水深度，h为坐标系原点深度，kr、mr为反射层数，

r1kr=((x-x0)2+(y-y0)2+(z-2krD+z0-2h)2)1/2,

r2kr=((x-x0)2+(y-y0)2+(z-2krD-z0)2)1/2，

r1mr=((x-x0)2+(y-y0)2+(z+2mrD-z0)2)1/2，

r2mr=((x-x0)2+(y-y0)2+(z+2mrD+z0-2h)2)1/2.

在第ns(ns=1,2,…,Ns)个电场传感器量测到的目标信号可建模为

(3)

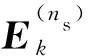
(4)

1.2 状态方程

根据观测方程定义k时刻船舶目标状态向量

(5)

式中：rk=[x,y,z]T；vk为目标在k时刻的速度，vk=[vx,vy]T，vx、vy是速度在x轴、y轴分量，忽略z轴方向上的运动。

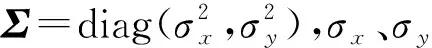
2 基于最大似然选择的滤波器组方法

2.1 基本原理

对于船舶SE跟踪问题，由于不知道滤波起始时目标的真实状态，滤波器组的基本思想便是假设目标真值是(或接近)多个假设初值中的一个，且概率相等，即

(6)

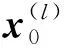
(7)

(8)

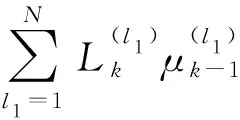
(9)

式中：

(10)

2.2 多初值模型参数确定

在全空间充满电导率为σ的导体媒质中，某场点处的电场模值为

(11)

由恒稳电场的镜像理论，在空气- 海水- 海床3层介质中，位于海水中的源在海水中产生的静态电场等效为无限大海水区域中源及其通过两个界面形成的无数个镜像在场点处产生的电场叠加。镜像的强度与源强度相同，只是与场点的距离发生变化。为此3层介质中电场模值的计算可以在源强度中加一个修正系数mc，mc可取一个经验值，与海水深度有关，则

(12)

那么由此便可以根据电场强度模值估算距离为

(13)

对于目标源强度，假设其分布在K个数量级上，在每个数量级上设置典型值。

(14)

式中：ψj为假设的目标方位角；i=1,2,3；j=1,2,3,4.

(15)

2.3 渐进更新扩展卡尔曼滤波

PUEKF算法思想来源于渐进贝叶斯理论[9-11]，本质在于逐步引入量测信息，关键在于重新设计扩展卡尔曼滤波算法的量测更新步骤。PUEKF算法将时间间隔[tk-1,tk]划分成Npu个子区间，而每个子区间的时间间隔为δλ=(tk-tk-1)/Npu，这相当于在[tk-1,tk]内插入Npu-1个伪时间序列，序贯获得Npu个观测值。观测更新过程在每个子区间内进行一次。时间间隔变化，观测噪声协方差也会发生变化。

(16)

结合卡尔曼滤波的基本步骤，可得PUEKF算法步骤：

1)时间更新。

Pk|k-1=FPk-1|k-1FT+Qk-1，
k|k-1=Fk-1|k-1，

2)观测更新。

②Foripu=1,2,…,Npu

Pipu=(I-KipuHipu-1)Pipu-1.

当Npu=1时，PUEKF退化为卡尔曼滤波。

综上所述，可给出滤波器组跟踪算法的步骤如下[13]：

(17)

5)对对数似然函数值进行归一化。

6)进行下一时刻滤波或在规定时刻结束滤波。

3 仿真结果及分析

设计仿真实验，以验证滤波器组方法在先验信息缺失条件下对船舶静电场跟踪的有效性。

电偶极子电偶极矩p=100 A·m；以传感器阵列为基础建立右手坐标系，传感器连线为y轴，传感器中心点为坐标原点，x轴过原点垂直于y轴，z轴向上；选用两个三轴电场传感器，其位置为o1和o2，船舶的其他初始状态如表1所示；此外，过程加速度噪声强度σx=σy=0.100，α=0.001；观测噪声协方差矩阵Rk=σ2I2×2，σ=1×10-7.

对滤波器组进行配置，假设目标源强度分布在K=3个等级上，即p1=50 A·m，p2=100 A·m，p3=200 A·m. 在各个距离上起始NF=4个PUEKF滤波器，各个滤波器的假设方位分别为π/4 rad、3π/4 rad、5π/4 rad、7π/4 rad.

表1 仿真场景参数

选择位置分量在k时刻总的均方根误差TRMSEk作为衡量算法优劣的标准，其定义为

(18)

式中：MC为仿真次数，MC=100；TN为跟踪滤波过程总的迭代次数；k为k时刻rk的后验估计值。

图1为滤波器组的总均方根误差，图2为滤波器组的对数似然函数值，图3为对数似然函数值最大的前3个滤波器(从大到小依次为7号、3号、11号)对应的跟踪结果。

图1 滤波器组的总均方根误差Fig.1 Total root mean square errors of filter bank

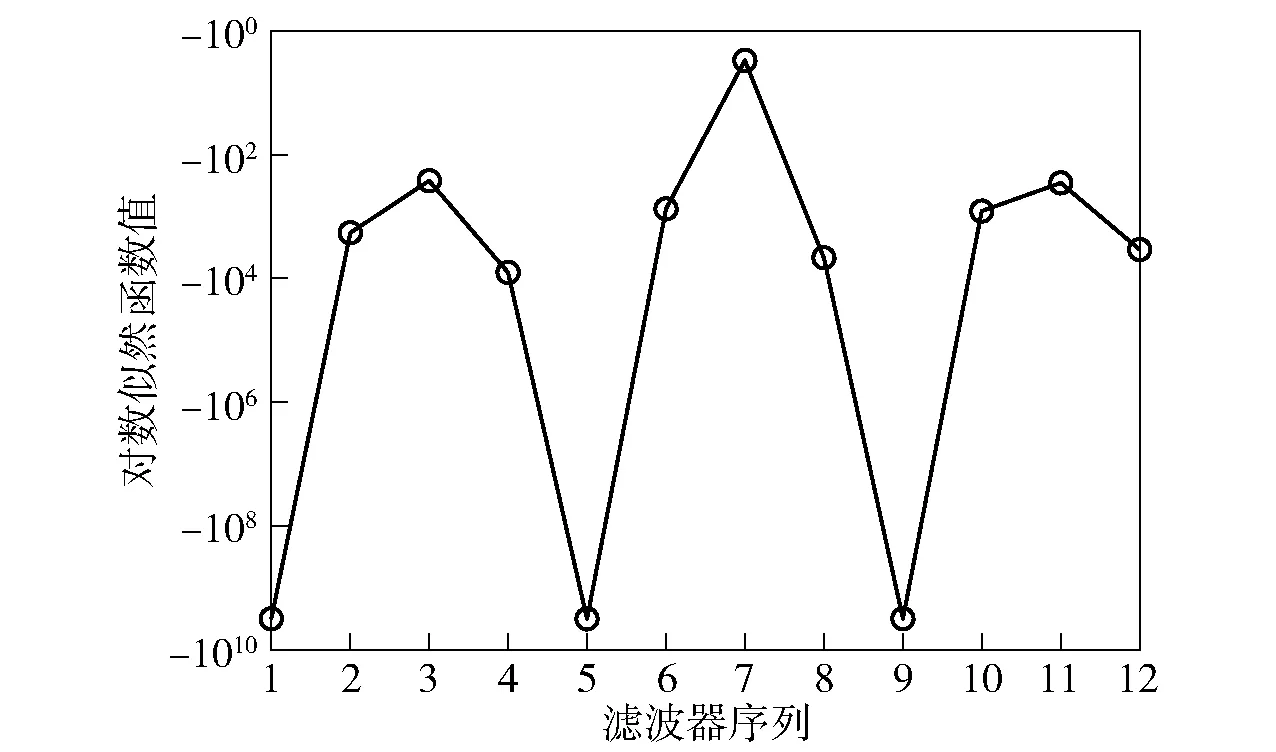
图2 滤波器组的对数似然函数仿真值Fig.2 Simulated values of logarithmic likelihood function of filter bank

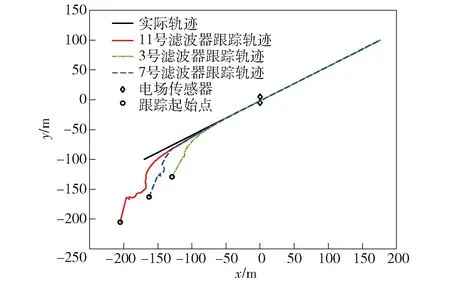
图3 滤波器组跟踪仿真结果Fig.3 Simulated results of filter bank tracking

同时可见，最大似然值对应的初假设(7号滤波器)正是电偶极矩最接近真实情况的初值假设，可以证明2.2节提出的初值确定方法是有效的。

4 实测实验

为验证上述理论，进行了电偶极子跟踪实测实验。

实验搭设两套相同的电场测量装置，电极采用Ag/AgCl电极，如图4所示是其中一套电场传感器，电极两两相对，取差分输出得到电场测量值；利用自制的超低噪声前置放大电路采集信号，利用数据记录仪采集数据。利用全球定位系统(GPS)对模拟源轨迹进行定位。

图4 二轴电场传感器Fig.4 Two-axis electric field sensor

以传感器阵列为基准建立右手坐标系，传感器阵列所在线为y轴，x轴垂直y轴指向其右侧，z轴向上。图5为实验示意图。海水深度8.4 m，海水电导率4.0 S/m，海床电导率0.4 S/m. 电场传感器阵列中两个传感器距离为10.0 m. 模拟源由电流源和发射电极组成，电流源置于木船上，提供电流，经发射电极输入海水中，发射电极位于水深0.2 m处，两个发射电极之间的距离为10.0 m，电流源输出电流10.0 A. 真实轨迹是GPS数据经WGS84地球坐标系转换成大地坐标系，然后坐标旋转到传感器坐标系下得到，作为参考。模拟源起始位置约为(-57.1 m,-280.0 m)，传感器坐标为(0 m,±5.0 m,0 m)。对滤波器组进行配置，假设目标源强度分布在K=3个等级上，即p1=50 A·m、p2=100 A·m、p3=200 A·m. 航向起始角设定为π/4 rad、3π/4 rad、5π/4 rad、7π/4 rad. 实验跟踪效果如图6～图8所示。图6为传感器测得的电场信号(滤波后)，图7为滤波器组的对数似然函数值，图8为对数似然函数值最大的前3个滤波器对应的跟踪结果。

图5 实验示意图Fig.5 Experimental schematic diagram

图6 模拟源电场信号Fig.6 Electric field signal from analog source

图7 滤波器组的对数似然函数实验值Fig.7 Experimental value of logarithmic likelihood function of filter bank

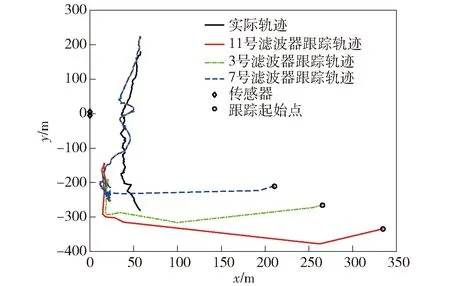
图8 滤波器组跟踪实验结果Fig.8 Experimental results of filter bank tracking

需要说明的是：

1)GPS定位精度相对较差，因此其记录的轨迹有较大波动，相比于真实轨迹其记录轨迹的位置坐标误差约在5 m左右；

2)渔船航行受浪影响较大，波动较大，因此模拟源运动并非假设的匀速直线运动，带有一定的机动特性；

3)跟踪轨迹无法与真实轨迹进行对准，从而无法计算TRMSEk，但从图8可以看出，跟踪轨迹基本收敛在参考轨迹附近。

实验结果表明，滤波器组算法可以有效的解决先验信息缺失条件下的船舶静电场跟踪问题。

5 结论

利用船舶静电场对船舶目标进行跟踪定位可以作为水声跟踪定位的一个有效补充。本文用电偶极子对船舶进行建模，建立船舶电场跟踪的状态空间模型，以渐进更新扩展卡尔曼滤波器为最基本的滤波单元，引入基于最大似然选择的滤波器组方法，以解决船舶静电场跟踪中先验信息缺失的问题，然后通过仿真和海上实测实验对其进行验证。仿真和海上实验结果均表明：滤波器组方法可以有效地解决先验信息缺失条件下的船舶静电场跟踪问题，最大似然选择法能够筛选出较优的跟踪轨迹；相比于距离，跟踪误差对方位先验信息更加敏感。本文首次进行了海上电偶极子跟踪实测实验，在实测环境下对跟踪滤波算法的有效性和船舶电场跟踪的可行性进行了验证，对船舶电场跟踪的发展应用具有一定的指导意义。