基于灰色理论和指数平滑法的备件需求预测模型研究

靳杰

【摘 要】 近年来需求预测问题已成为热点问题，也成为各企业的重点工作任务。科学准确的需求预测可以降低仓储成本、增加库存周转率以及减少库存停滞，这对提高企业的竞争实力来说至关重要;而设备维修备件需求预测不仅影响着设备的正常运行，还可能会因预测问题给企业造成巨大的损失。文章在分析了很多学者研究备件需求预测的基础上，基于现场项目备件物资使用频次、备件价格对备件物资进行分类，分类级别体现了備件的重要性，对级别最高的备件提出了一种简单易操作可用于指导企业生产实践且预测性较高的组合预测模型。以此构建基于灰色理论与指数平滑法的需求预测综合模型，对S公司某种备件的需求量进行科学准确的预测。研究表明，基于灰色理论与指数平滑法的需求预测综合模型相对单一预测模型具有较高的可靠性与实用性，能为S公司生产决策提供科学的保障。

【关键词】 需求预测 灰色模型 指数平滑法

1 引言

备件，也称备用件，是在设备维修工作中，根据设备的磨损与寿命，将设备中容易磨损的各种零部件加工、采购和存储好，这些零部件称为备件。备件库存成本居高不下是生产制造企业面临的最大问题，造成企业维修资金的积压主要存在的原因包括：领导者没有预测的思想以经验为主，预测方法较为复杂实用性差。随着我国制造企业的飞速发展，制造企业对需求预测越来越重视，同时也吸引了越来越多国内外学者对需求预测进行研究。李树广和徐诚[1]等运用粗糙集协调近似表示空间模型方法对某部队特种装备的维修备件进行了需求预测;刘喜春和祝龙石[2]研究了基于模糊推理的战时备件需求预测方法，把专家预测值和Markov预测值结合起来，最终备件需求预测值使用Mamdani 模糊推理规则以及反模糊化求出;赵建忠和朱伟等[3]根据导弹装备故障规律来预测导弹备件消耗，建立了导弹装备故障次数灰色预测模型。但单一预测模型预测性不高，预测值与实际值之间偏差较大，因此很多学者都会对单一模型进行改进组合，之后再进行预测。赵建忠[4]等将灰色理论模型和ARMA模型组合对导弹装备备件需求进行预测;高鹍和邢国平等[5]提出一种基于灰色关联分析和支持向量机回归相结合针对性的对机体不同备件库存消耗预测的方法，预测精度较高;夏秀峰和董彦军[6]针对时间序列法却在较大误差的缺陷，通过马尔科夫预测和改进的三步平均马尔科夫预测法预测分析航空备件的需求状态概率;董骁雄和陈云翔[7]等针对后续备件需求预测精度低的问题，提出一种基于模糊软集合和贝叶斯的后续备件组合预测方法。在国外的备件需求预测研究中，Croston[8]同时考虑历史需求量和需求时间间隔，创新性的提出将不常用备件需求序列分为需求量和需求间隔两个连续序列来分别进行预测;Maria Franco-Villoria和Rosaria[9]用Bootstrap允许评估预测曲线的不确定性空间相关函数处理数据。

综上所述，虽然方法组合模型提高了预测准确度但是由于其算法复杂而且预测方法很多基于大量数据对于各个企业使用起来不切实际，因此本文在单一模型预测性不高以及组合模型实用性差的基础上提出了一种基于灰色理论与指数平滑法的需求预测综合模型，简单易操作可用于指导企业生产实践，使得备件库存结构趋于合理化。

2 模型构建

2.1 灰色系统理论

华中科技大学控制科学与工程系教授邓聚龙于1982年提出并创立了新兴学科-灰色系统理论，它的作用是解决某些涉及未知因素的问题。灰色系统理论研究的是贫信息建模，它提供了少量信息下解决系统问题的新途径。

2.2 建立GM（1，1）模型

对数列X（0）做一次累加生成X（0）的1-AGO 序列

2.3 建立二次指数平滑法的预测模型

指数平滑法是生产预测中常用的一种方法，同样在时间序列预测中也经常使用，二次指数平滑法是在一次指数平滑的基础上再做一次指数平滑， 比较适合带有线性趋势且周期性表现又不是很明显的时序可以提高预测结果的精度[9]，公式为

2.4 建立综合预测模型

现假设系统已经根据n个原始数据构建了GM（1，1）模型，结合二次指数平滑模型，用权重预测法构建综合预测模型：

3 模型应用

S公司是国内风机业务企业，其生产主要为按订单生产类型与提前生产类型兼容以此满足客户需求。由于呆滞库存占用较大比例库存成本较高，因此高准确地预测对S公司降低成本提高企业竞争力至关重要。已知2017年1月至2017年7月各月份某维修备件消耗数量分别是：724、746、778、800、827、871、912。

3.1 GM（1，1）模型预测

对1月到7月需求数据建立GM（1，1）模型可得系数a=-0.039，b=699.46。代入模型可得：

由以上公式可预测8-12月的消耗量分别为：942、980、1020、1061、1104。

GM（1，1）模型误差如表1所示。

由表1实际值与预测值比较发现，灰色模型的预测结果还是比较满意的，能够较好的拟合，但是灰色模型的发展系数限制了模型预测时间的长短。

通过分析可以得到以下结论：

当-a≤0.3时，GM（1，1）可用于中长期预测;

当0.3<-a<0.5时，GM（1，1）可用于短期预测;

当0.5<-a≤0.8时，作短期预测时应十分谨慎;

当0.8<-a≤1时，应采用残差修正模型;

当-a>1时，不宜采用灰色模型

因此运用GM（1，1）首要前提是确定发展系数的大小。

3.2 二次指数平滑法预测

平滑系数会直接影响预测结果，因此平滑系数的选取非常关键。当时间序列处于相对稳定水平趋势时应选较小值可在0.05-0.20间取值;当其虽短时有波动但长时间变化不大时可在0.1-0.4间取值;当其长期波动较大时，应在0.6-0.8取值;当时间序列数据呈上升或下降趋势时，平滑系数可以取0.6-1之间的值。

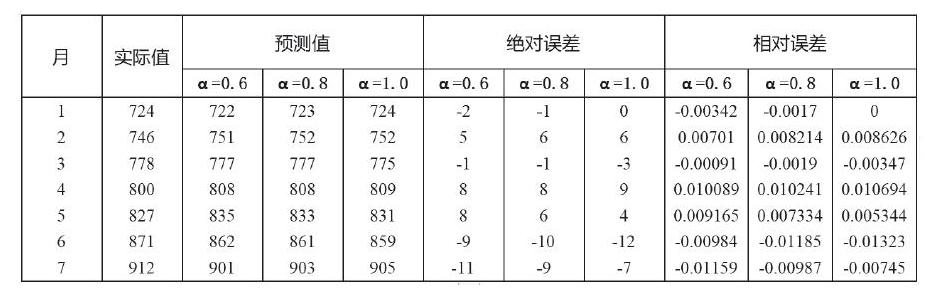
指数平滑法误差（=0.6、0.8、1.0 时）

在的情况下，根据公式可以预测出8-12月各月需求为946，983，1022，1062，1103个。

由以上表格数据我们得出，灰色预测模型GM（1，1）比指数平滑法预测精度高，故灰色预测模型比指数平滑法在单一预测中使用广泛，综合预测模型中用GM（1，1）模型计算出的权重比二次指数平滑法预测模型计算出的权重高，GM（1，1）模型与二次指数平滑法预测模型的权重比值选择为0.95：0.05，由公式计算组合预测模型各预测值。

由以上表格中误差比较可以发现，用综合预测模型求出的绝对误差、相对误差、平均绝对偏移、平均绝对百分比误差均优于用单一的灰色预测模型和二次指数平滑模型求出的误差，由此结果我们预测出8-12 月的需求量分别为：943，981，1020，1061，1104 （單位：个）。根据以上测结果，我们得出结论：S公司需要对其现有的库存进行管理，同时还要按照之前预测出的需求量制定生产计划。

4 总结

在这样一个数据信息无时无刻都在产生的时代，各个企业应该利用数据为企业的发展服务。虽然预测与实际之间存在偏差，但是对于企业而言进行需求预测还是有利可图的，采用科学有效便于操作的模型不仅是预测成败的关键，而且有利于生产商制定生产决策。本文提出的基于灰色理论与指数平滑法组合模型在绝对误差、相对误差、平均绝对偏差和平均绝对百分比误差四个方面均比单一模型的预测结果小，因此该组合模型不仅具有理论研究意义，而且对于企业的生产决策具有实际指导作用，为企业的发展提供有力的保障。

【参考文献】

[1] 李树广，赵彦峻，徐诚. 装备维修备件需求预测与决策方法研究[J]. 兵工学报，2011，32（07）：901-905.

[2] 刘喜春，祝龙石，张伟. 基于模糊推理的战时备件需求预测[J]. 兵工学报，2013，34（09）：1197-1200.

[3] 赵建忠，朱伟，徐恒博，刘勇. 基于故障规律的导弹备件消耗预测[J]. 战术导弹技术，2012，（05）：44-49.

[4] 赵建忠，徐廷学，李海军，叶文. 基于小波分析的导弹装备备件需求组合预测[J]. 电子学报，2014，42（03）：417-423.

[5] 高鹍，邢国平，孙德翔，黄勇. 灰色关联支持向量机在备件库存消耗预测中的应用[J]. 电光与控制，2012，19（03）：100-105.

[6] 夏秀峰，董彦军. 基于改进马尔科夫模型的航空备件需求预测[J]. 兵工自动化，2013，32（11）：39-41+48.

[7] 董骁雄，陈云翔，张玮玉，张帆.基于模糊软集合和Bayes的后续备件组合预测方法[J].南京航空航天大学学报，2018，50（05）：672-678.

[8] Croston J D. Forecasting and stock control for intermittent demands[J].Journal of the Operational Research Society，1972，23（ 3） ： 289-303.

[9] Maria Franco -Villoria，Rosaria Ignaccolo. Bootstrap based uncertainty bands for prediction in functional kriging[J]. Spatial Statistics，2017，21（ 8） ： 130-148.