再入飞行器滑翔段精确减速控制技术*

范世鹏 王 亮 贾静雅 李 伶 刘晓东

1.北京航天自动研究所，北京100854 2. 首都航天机械公司，北京 100076

为满足复杂的现代战争需求，再入飞行器必须满足多种终端约束条件。制导技术的内涵不仅仅停留在命中精度层面，还要将终端速度控制在指定的范围内，以创造良好的末端探测条件。例如，潘兴II弹头必须减小弹道末端的飞行速度，以免被严重的气动加热所产生的等离子体形成信号屏障，导致弹上雷达无法正常工作[1]。

气动减速是在制导指令中叠加额外的附加攻角，利用气动阻力进行减速，是工程上常用的一种有效方法。同时，产生的有界振荡指令在一定程度上可以提高导弹突防的能力[2]。连葆华等采用变结构控制方法，对速度进行控制[3]。但这种减速方法没有充分地利用弹上加速度信息，对速度的控制精度较差。

周荻等为实现导弹突防，将正弦指令作为参考输入，并推导得到一种滑模制导律，使导弹在机动突防后仍可以精准命中目标[4]。Xue等研究了再入飞行器的预测校正制导，实质上是通过全程的高度剖面实现对速度的控制，但该算法的计算量相对较大[5]。刘鹏云等以锥形减速满足火箭弹对终端速度的要求，但所设计虚拟目标的运动规律可能因火箭弹阻力特性而无法实现[6]。李强和陈思远等提出一种大气预估的方法，以正弦规律的侧向附加机动控制速度，同时以最优制导律保证落点和落角约束，但需要根据当前状态在线预测终端速度，会增加弹上计算量[7-8]。陈安宏等以侧向机动实现减速，解决了平飞段速度控制问题[9]，然而，实际工程很少采用平飞，而以特定弹道倾角的滑翔飞行。王洁瑶等在合理的假设下，推导了准平衡滑翔段的弹道近似解，具有很好的参考价值，但未给出速度的解析公式[10]。

本文针对再入飞行器滑翔段减速控制问题，充分利用速度、阻力加速度等导航与测量信息，提出一种气动精准减速的可行方法。首先,考虑重力的影响，修正了滑翔段理想速度关于高度的解析表达式;其次，分析了减速回路与传统制导回路之间的关系，提出一种减速回路设计方法，针对2个回路耦合的特点，提出相应的控制策略。

1 理想速度解析表达式

为便于研究，常将空气密度视为飞行高度的双参数指数函数：

ρ=ρ0e-h/hs

(1)

其中，ρ0=1.752;hs=6.7×103。

图1对比了标准的大气密度与拟合高度-密度公式;图2给出了大气密度拟合的绝对误差和相对误差。

图1 拟合公式得到的大气密度近似值与实际值

图2 拟合公式近似的相对误差与绝对误差

根据以上分析，在高度5km～25km的大气拟合精度绝对偏差和相对偏差均较小，同时，适宜飞行器实现滑翔飞行。

在数学模型中，关于速度和高度相应的微分方程可表示为：

(2)

其中，m为质量;V为飞行速度;h为飞行高度;Cx为平衡滑翔攻角对应的气动阻力系数;ρ0为空气密度;S为参考面积;g为重力加速度;θ为弹道倾角。

对于平衡滑翔弹道，可将弹道倾角视为常值。且平衡攻角为常值，因此，将Cx视为常数。用式(2-1)除以式(2-2)，可得H-V空间的微分方程为：

(3)

可以看出，上述微分方程为伯努利方程的形式，可变形为：

(4)

变量代换w=V2，则：

(5)

若终端速度为Vf，则通过求解上述微分方程可得，高度在h到hT区间内：

(6)

其中，K可视为常值，其表达式为：

(7)

假设弹头无阻力，则K=0，代入上式可得：

(8)

可以看出，上式为机械能守恒定律。若忽略重力的影响，设g=0，则上式变为：

V(h)=VfeK(e-hT/hs-e-h/hs)

(9)

式(8)为传统锥形减速所采用的理想速度解析表达式。

由于滑翔段飞行时间较长，重力影响较大，因此，理想速度的推导必须考虑重力因素的作用。由于式(6)中关于重力项无法解析求解，对该项采用高精度的多项式逼近。

由麦克劳林公式可知，

(10)

其中，N取正整数。由式(9)可知，若x/N趋近于0时，则截断误差接近于0，即N的取值应根据x来确定。一般的，x/N<0.1。

为方便推导，记：

μT=e-hT/hs，μ(h)=e-h/hs

(11)

利用式(9)处理式(6)中的重力项，可得：

(12)

将式(11)中多项式展开后积分，可得：

(13)

则考虑重力的理想速度表达式为：

(14)

2 减速控制技术

这里将为保证落点、落角等终端约束而形成的制导回路称为传统制导回路，制导律可采用弹道成型等一类最优制导律，在此不做深入研究。由于减速控制回路与传统制导回路都是通过产生攻角来消除控制偏差，记ηc0,ηc1,ηc和η分别为传统制导回路合攻角指令、减速回路合攻角指令、最终的合攻角指令和弹体合攻角响应，则2个回路的耦合关系如图3所示：

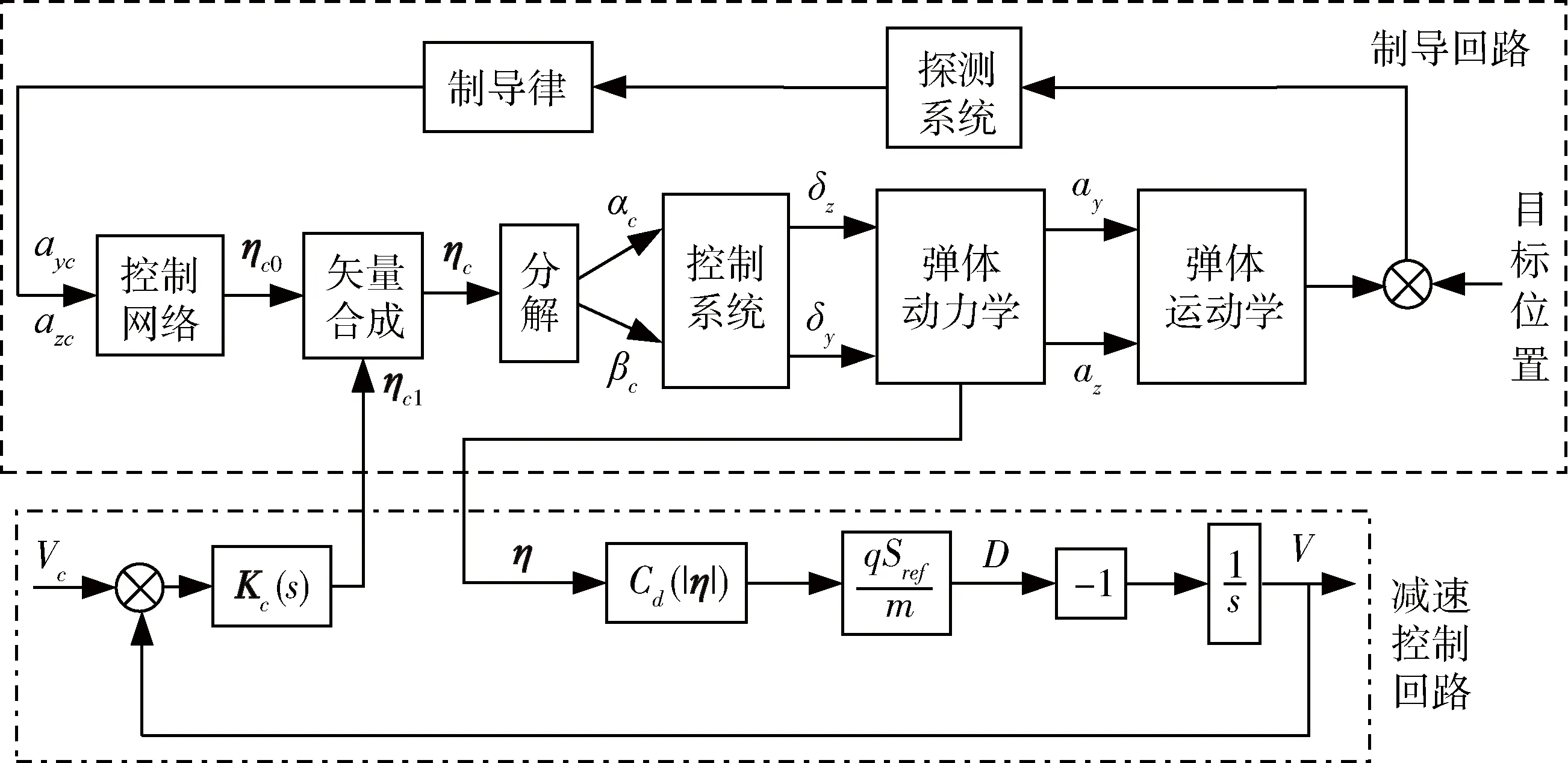
图3 制导与控制系统框图

记阻力系数为Cd，减速回路控制器Kc可设计为关于速度跟踪误差比例-积分-微分的PID形式，为加快跟踪回路的响应速度，省略积分项而采用比例-微分PD形式：

ηc1=K(Vn-Vc)+KD(Dc-Dm)

(15)

其中，Kv和KD分别为比例项和微分项的增益，Vn和Dm分别为速度导航值、阻力加速度测量值，Dc为当前期望阻力加速度，由下式求得：

(16)

可采用零极点配置来获得Kv和KD，考虑到速度的惯性较大，而攻角为快周期变量，因此，设计减速回路增益时，可忽略攻角响应的动态过程，则此时减速回路的特征方程为：

s2+KvCdSref/ms+KDCdqSref/m=0

(17)

同时，减速回路增加一个零点，P0=-KD/Kv，可用于调节动态特性。

鉴于主要的未建模环节(弹体动力学)频率一般为20rad/s左右，而速度的惯性较大，可将速度控制回路的特征频率配置在5～10rad/s，阻尼大于0.8。由根轨迹重心不变原理，弹体动力学对应的极点右移量小于10rad/s。所有极点均位于左半平面，从而保证控制系统的收敛性。

显然，若传统制导回路的合攻角指令不小于减速回路合攻角指令时，前者为保证落点、落角精度而进行机动飞行，已经达到了当前时刻减速的要求，无需生成减速回路的附加指令，此时采取“沿用传统制导指令作为最终的指令”的策略，即ηc=ηc0。

若传统制导回路的合攻角指令小于减速回路合攻角指令时，则需要在垂直于ηc0的垂直方向上叠加一个合攻角指令Δηc，使最终的合攻角指令为|ηc|=|ηc1|，则分解到俯仰和偏航通道的攻角与侧滑角指令分别为：

(18)

图4给出了上述情形下的2个回路合攻角指令关系的示意图。

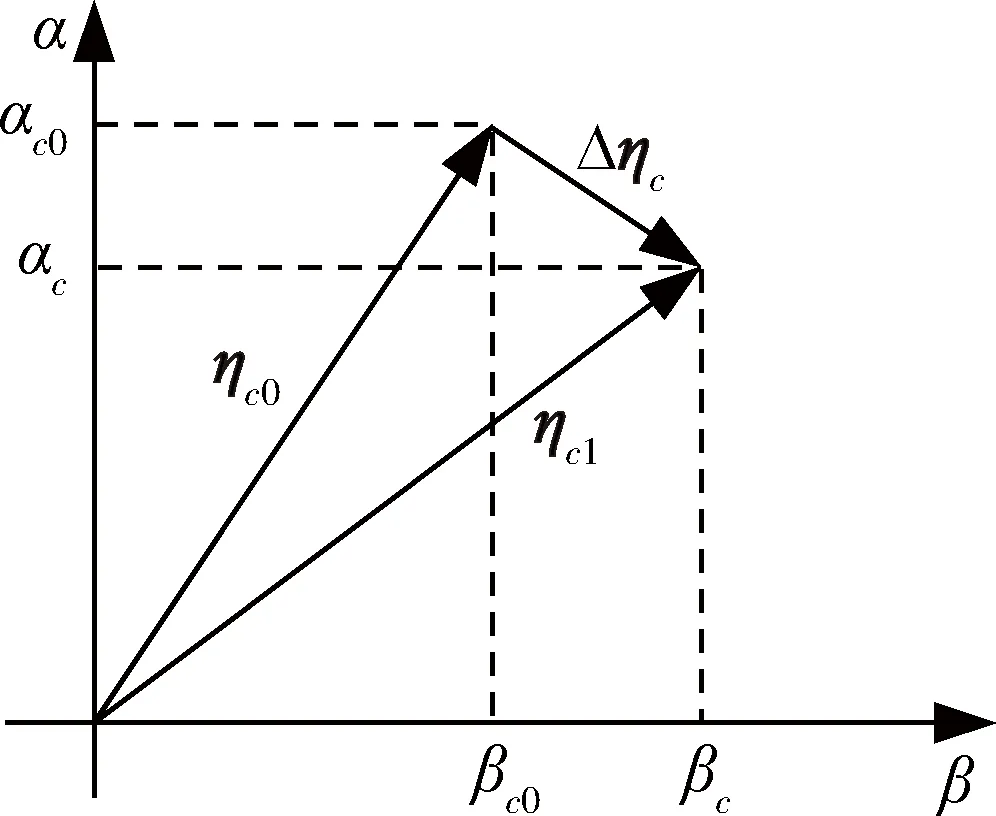
图4 控制指令合成示意图

对于传统制导回路而言，减速回路所产生的附加攻角指令是一种干扰，将造成弹目运动位置、速度的偏差。由于制导回路将逐渐主动消除偏差，因而会形成合攻角在空间的锥形运动。

3 仿真验证

采用六自由度非线性模型进行数学仿真验证，飞行器数学模型采用最大升阻比为1.5的气动布局。初始高度为27000m，初始弹道倾角为-10°，初始速度为2220m/s，在25～5km范围内引入锥形减速回路，要求落点精度优于10m，期望落速为550m/s±100m/s，传统制导回路采用弹道成型。图5～8给出了在引入和未引入减速回路2种条件下的弹道重要变量仿真结果。

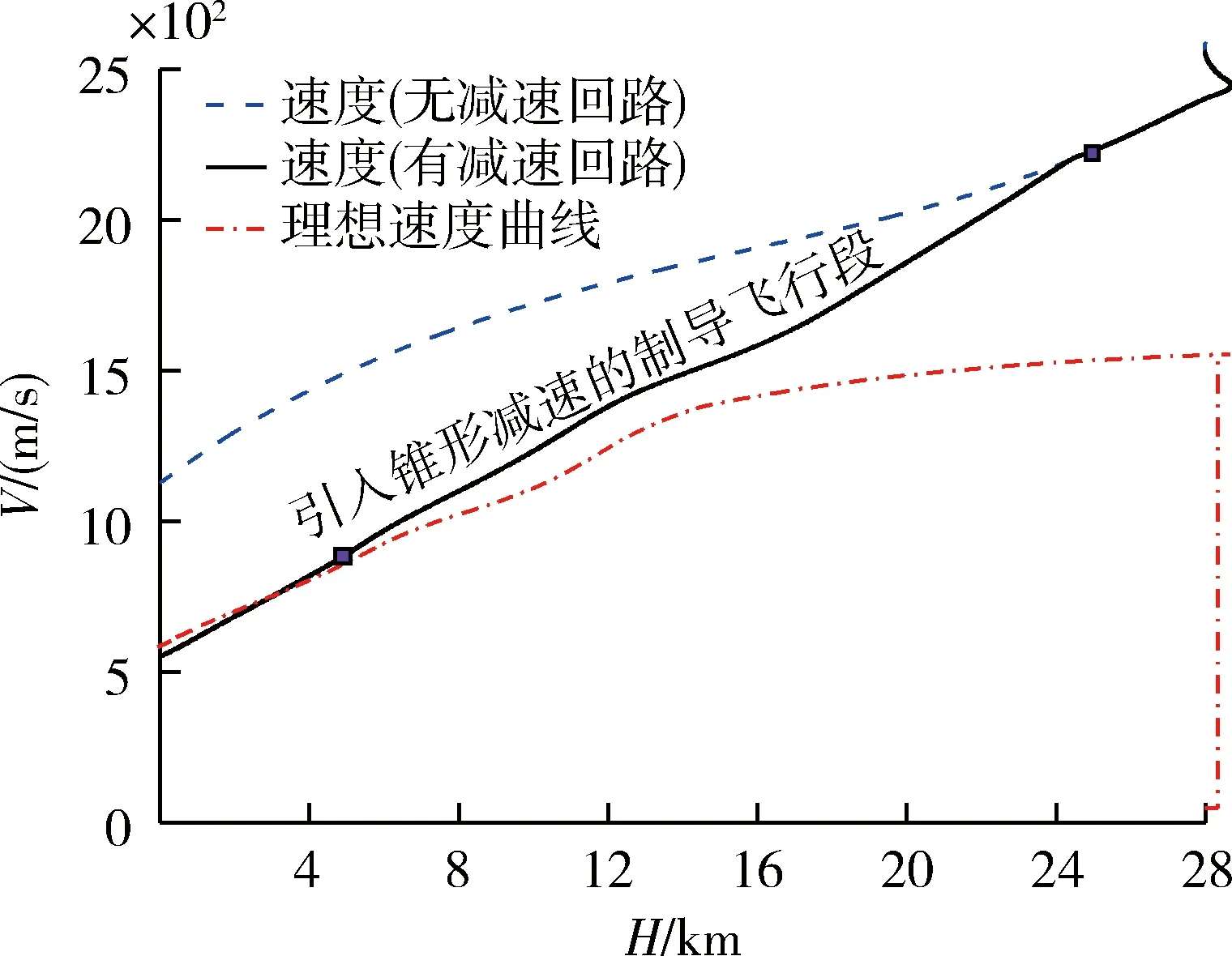
图5 V-H空间的实际速度与理想速度

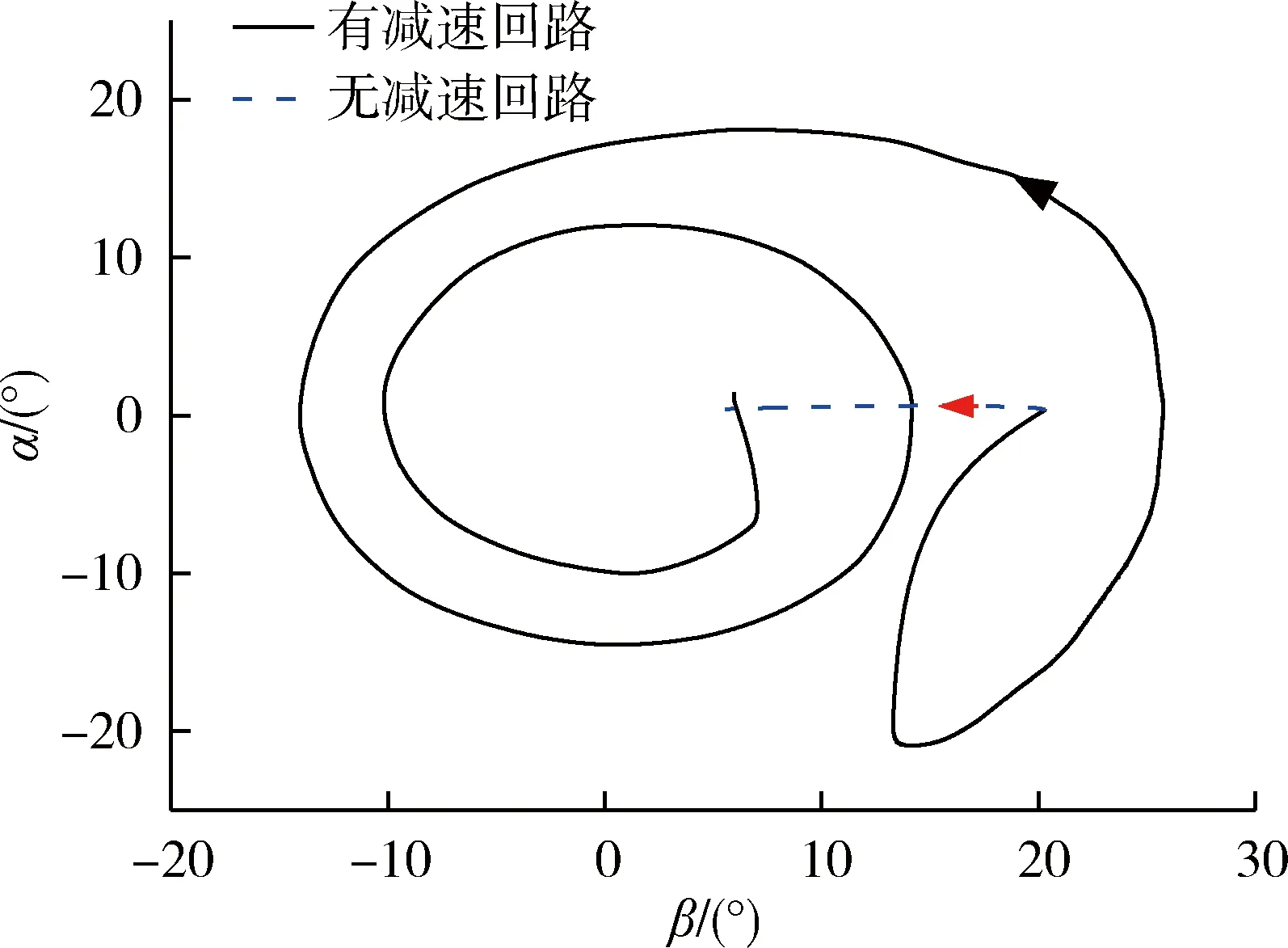
图6 减速段攻角与侧滑角的相轨迹

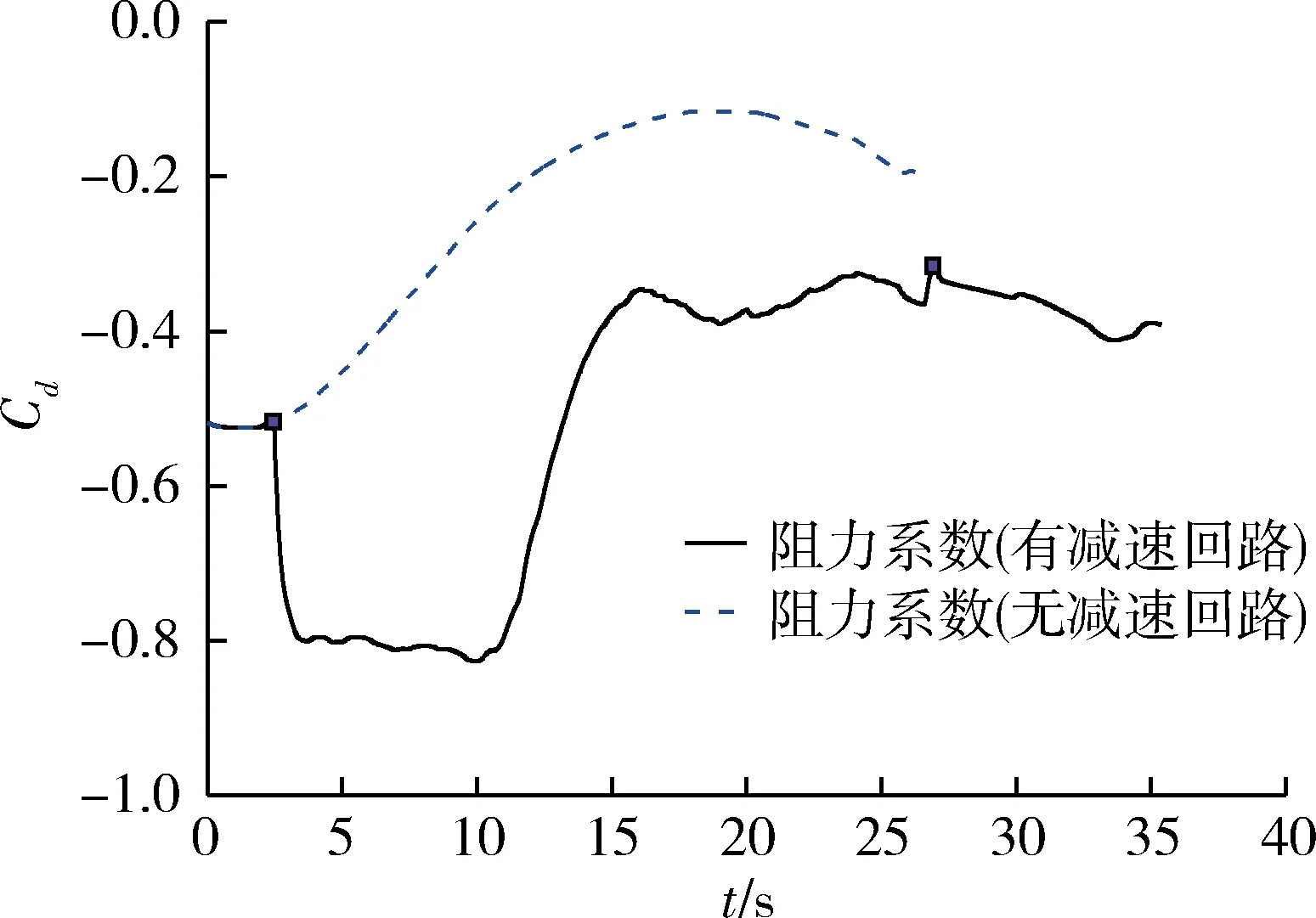
图7 阻力系数Cd曲线

图8 高度H曲线

从仿真结果可以看出，当引入减速回路后，飞行时间变长，通过攻角与侧滑角交替锥形运动，使飞行过程中气动阻力系数增大，从而使终端速度满足要求。在滑翔段25km降至5km的过程中，在引入和不引入减速回路2种条件下，减速回路对速度剖面进行了大幅度的调整，两者的终端速度分别为552m/s和1128m/s，由此可见，通过气动减速是一种有效的速度控制手段。

4 结论

随着再入飞行器控制技术的不断发展，满足终端速度、位置及攻击角度等要求的多约束制导方法始终是该领域的关键技术。本文根据滑翔段的特点，在合理假设下，以高度为自变量的滑翔段速度运动规律具有解析形式，同时由于飞行器导航系统可以获取高度信息，这种方法适用于实际工程中的速度控制。由于传统制导回路与减速控制回路相互影响，本文在设计减速回路控制律的同时，制定了有效的控制策略，在不影响打击精度的前提下，实现了终端速度的精准调节。